高考数学模拟试题（六）

李青云

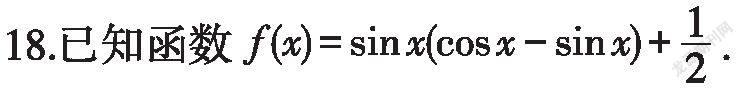
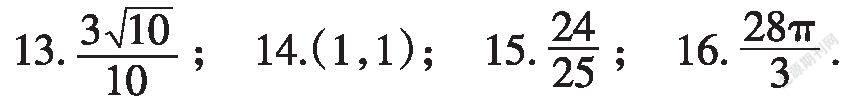
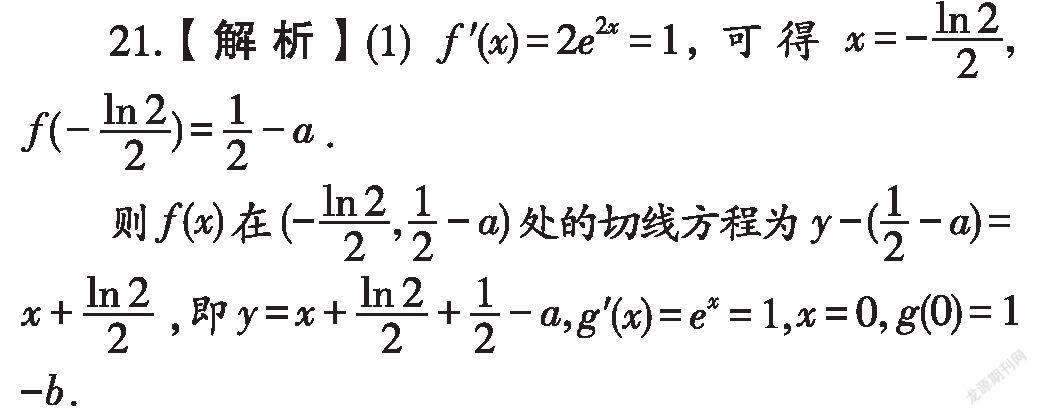
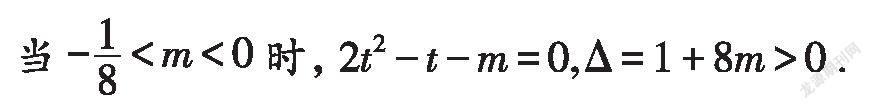
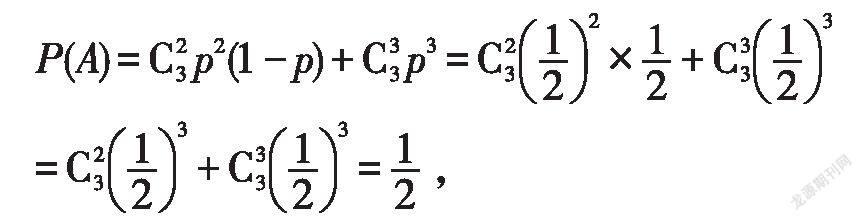
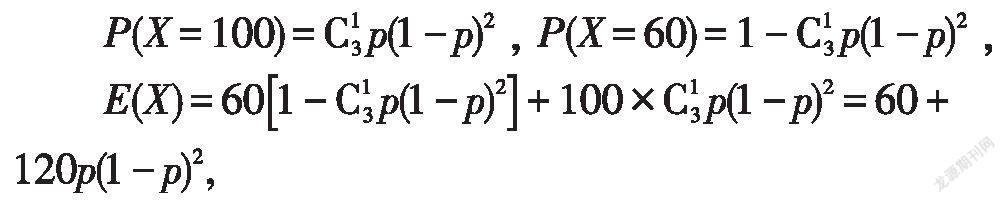
一、单项选择题

A.第一象限    B.第二象限

C.第三象限    D.第四象限

3.若干年前，某老师刚退休的月退休金为4000元，月退休金各种用途占比统计图的条形图如图1所示.该老师退休后加强了体育锻炼，目前月退休金的各种用途占比统计图的折线图如图2所示.已知目前的月就医费比刚退休时少100元，则目前该老师的月退休金为（）.

A.5000元    B.5500元    C.6000元    D.6500元

7.若函数f（x）同时满足：①定义域内存在实数x，使得f（x）·f（-x）<0;②对于定义域内任意x，x，

当x≠x时，恒有（x-x）·[f（x）-f（x）]>0;则称函数f（x）为“DM函数”.下列函数中是“DM函数”的为（）.

A.f（x）=x    B.f（x）=sinx

C.f（x）=e    D.f（x）=lnx

二、多项选择题

9.若10=4，10=25，则（    ）.

A.a+b=2    B.b-a=1

C.ab>8lg2    D.6-a>1g6

10.下列关于圆锥曲线的命题中，正确的是（）.

C.方程2x-5x+2=0的两根可分别作为椭圆和双曲线的离心率

12.某校实行选课走班制度，张毅同学选择的是地理、生物、政治这三科，且生物在B層，该校周一上午选课走班的课程安排如下表所示，张毅选择三个科目的课各上一节，另外一节上自习，则下列说法正确的是（）.

的对边，且满足acos2B=acosB-bsinA，求f（A）的取值范围.

（1）求证：平面BDDB⊥平面CDDC;

（2）求二面角C-BD-C的余弦值.

A.此人有4种选课方式

B.此人有5种选课方式

C.自习不可能安排在第2节

D.自习可安排在4节课中的任一节

三、填空题

四、解答题

17.设{a}为等差数列，{b}是正项等比数列，且a=b=2，a=2b.在①b-b=12b，②a+2=b，③logb=logb+1，n≥2，n∈N这三个条件中任选一个，求解下列问题：

（1）写出你选择的条件并求数列{a}和{b}的通项公式;

（2）在（1）的条件下，若c=a·b（n∈N），求数列{c}的前n项和S.

（1）求f（x）的单调递减区间;

（2）在锐角△ABC中，a，b，c分别为角A，B，C

（1）求抛物线C的方程;

21.已知函数f（x）=e-a，g（x）=e-b，且f（x）与g（x）的图象有一个斜率为1的公切线（e为自然对数的底数）.

（1）求b-a;

22.垃圾分类后，大部分运往垃圾处理厂进行处理.为了监测垃圾处理过程中对环境造成的影响，某大型垃圾处理厂为此建立了5套环境监测系统，并制定如下方案：每年工厂的环境监测费用预算定为80万元，日常全天候开启3套环境监测系统，若至少有2套系统监测出排放超标，则立即检查污染处理系统;若有且只有1套系统监测出排放超标，则立即同时启动另外2套系统进行1小时的监测，且后启动的这2套监测系统中只要有1套系统监测出排放超标，也立即检查污染处理系统.设每个时间段（以1小时为计量单位）被每套系统监测出排放超标的概率均为P（0<P<1），且各个时间段每套系统监测出排放超标情况相互独立.

（2）若每套环境监测系统运行成本为20元/小时（不启动则不产生运行费用），除运行费用外，所有的环境监测系统每年的维修和保养费用需要6万元.现以此方案实施，问该工厂的环境监测费用是否会超过预算（全年按9000小时计算）？并说明理由.

参考答案与解析

一、单项选择题

1-8    ADABD    CAC

二、多项选择题

9.ACD;10.CD;ll.BD;12.BD.

三、填空题

四、解答题

17.【解析】（1）选择①：设{a}的公差为d，{b}的公比为q（q>0）.

所以a=2+3（n-1）=3n-1，b=2·2=2;

选择②：设{a}的公差为d，{b}的公比为q（q>0）.

所以a=2+3（n-1）=3n-1，b=2·2=2.

则{b}的公比为q=2，又2+2d=4q，∴d=3，

所以a=2+3（n-1）=3n-1，b=2·2=2.

（2）由（1）可知c=（3n-1）·2，

S=2·2+5·2+8·2+…+（3n-l）·2①，

2S=2·2+5·2+…+（3n-4）2+（3n-1）2②，

①-②得-S=2·2+3·2+3·2+…+3·2-（3n-1）·2=4+3（2+2+…+2）-（3n-1）2，

（2）由正弦定理得sinAcos2B=sinAcosB-sinBsinA，

∵sinA≠0，∴cos2B=cosB-sinB，

即（cosB-sinB）（cosB+sinB）=cosB-sinB，

（cosB-sinB）（cosB+sinB-1）=0，

得cosB-sinB=0，或cosB+sinB=1，

所以∠BDC=90°，即BD⊥CD.

因为AA⊥底面ABCD，

所以DD⊥底面ABCD，所以BD⊥DD.

所以BD⊥平面CDDC，

所以平面BDDB⊥平面CDDC.

（2）分别以DB，DC，DD为x，y，z轴，建立空間直角坐标系D-xyz，

由图知二面角C-BD-C为锐角，

设M（x，y），N（x，y），将直线MN的方程代入x=2py中，得x-2px-p=0，

因此x+x=2p，xx=-p.

由题意和切线的几何意义知，曲线C在T处的切线斜率即导数为1，因此得t=p，

将x+x=2p，xx=-p代入其中，

因此所求的抛物线方程为x=4y.

（2）显然，直线AB的斜率一定存在，

设AB的方程为y=kx+b，A（x，y），B（x，y），

故xx+（kx+b）（kx+b）=-4，

也即（k+1）xx+kb（x+x）+b+4=0，①

将y=kx+b代入抛物线C中，

得x-4kx-4b=0，

故x+x=4k，xx=-4b.

将它们代入到①中，得（k+1）（-4b）+kb·4k+b+4=0，解得b=2，

因此直线AB恒过点（0，2）.

则g（x）在（0，1-b）处的切线方程为y-（1-b）=x，y=x+1-b，

（2）由（1）可得h（x）=e-e-mx，h′（x）=2e-e-m，

令t=e，则y=2t-t-m，

Δ=1+8m，当m>1时，2t-t-m=0有两根t，t，且t<0<t，

h′（x）=2（e-t）（w-t）=0，得x=lnt，

在（-∞，lnt）上，h′（x）<0，在（lnt，+∞）上，

h′（x）>0，此时，h（lnt）<h（0）=0.

又x→-∞时，h（x）→+∞，x→+∞时，h（x）→+∞故在（-∞，lnt）和（lnt，+∞）上，

h（x）最小值为h（0）=0，故h（x）仅有1个零点.

当0<m<1时，h′（x）=2（e-t）（e-t），其中t<0<t，当m&gt;l时，h（x）在（-∞，lnt）与（lnt，+∞）上，h（x）各有1个零点，

当m=0时，h（x）=e-e，仅在h（0）=0时有1个零点，

方程有2个正根t，t，h′（x）=2（w-t）（e-t）.

在（-∞，lnt）上，h′（x）>0，在（lnt，lnt）上，h′（x）<0，在（lnt，+∞），h′（x）>0.

故lnt<0，h（lnt）<h（0）=0.

h（lnt）=t-t-mlnt=t[（t-1）+（1-2t）lnt]，

因為t-1<0，1-2t>0，lnt<0，故h（lnt）<0.

故在（-∞，lnt）上，h（x）<h（lnt）<0，

在（lnt，lnt）上，h（x）<0，在（lnt，+∞）上，h（x）有1 个零点：x=0.

则h（x）为增函数，h（x）仅有1个零点：x=0.

综上可得，当m≤0或m=1时，h（x）有1个零点，当0<m<1或m>1时，h（x）有2个零点.

22.【解析】（1）设某个时间段在需要开启3套系统就被确定需要检查污染源处理系统的事件为A，

设某个时间段在需要开启另外2套系统才能确定需要检查污染源处理系统的事件为B，

（2）设某个时间段环境监测系统的运行费用为X

元，则X的可能取值为60，100.

令g（p）=p（1-p），p∈（0，1），

则g′（p）=（1-p）-2p（1-p）=（3p-1）（p-1），

而76<80，故不会超过预算.