分档电价和碳配额激励的含电动汽车微电网优化调度策略
2022-07-10李咸善鄂璇
李咸善, 鄂璇
(三峡大学梯级水电站运行与控制湖北省重点实验室, 宜昌 443002)
随着能源消耗与日俱增导致逐渐枯竭,电动汽车(electric vehicle,EV)作为一种环保、低碳的出行工具,不断得到广泛应用[1]。近年来,电动汽车并网技术的日臻成熟,电动汽车在微电网中的渗透率也将不断提升[2],其时空的分散性和充电行为所具有的随机性和不确定性会增大微电网原有的负荷峰值,导致“峰上加峰”,给微电网带来巨大的调度压力[3]。为了缓解此现象,需要通过电动汽车与微电网的良性互动,采用适当的激励政策引导电动汽车有序充放电以实现微电网需求侧管理、促进新能源消纳。其中,基于电价的激励政策是常见的需求侧管理手段,目前主要包括分时电价和实时电价政策。但以分时电价为激励手段会导致电动汽车的过响应现象,造成新的峰谷差[4];在实时电价的引导下,会导致电动汽车响应疲惫的现象,造成新的负荷尖峰比[5]。基于上述现象,提出一种分档电价(ladder electricity pricing,LP)激励手段,根据净负荷大小分成多个档位电价,对不同净负荷大小实施不同的激励力度。重点研究基于分档电价的含电动汽车微电网的优化调度策略,通过分档电价和碳排放配额的激励政策引导优化电动汽车充放电行为的适度响应,提高电动汽车与微电网侧双方效益。
目前,学者们针对电动汽车参与电网优化调度开展了大量研究[6-9]。文献[10]充分考虑电动汽车充放电的特征,对分时充电电价模型进行了优化,能够有效提升新能源消纳能力。文献[11]引出碳排放问题是当今电网中关注的重点问题,将碳交易引入到热电联系统中,构建了交易模型,有助于降低碳排放量。文献[12-14]仅采用电价机制去引导电动汽车的响应,激励形式较为单一。文献[15]将碳交易引入电动汽车的优化调度中,通过仿真验证了获得碳配额的电动汽车参与优化调度后,既降低了用户成本,也达到了减碳的目的。文献[16]运用博弈的思想,在智能小区中,建立了代理商与车主的主从博弈模型,实现了多主体之间的利益平衡。
基于上述研究背景,以微电网优先消纳新能源为原则,提出了根据各时段净负荷大小制定的分档电价模型与碳配额奖励机制;建立了以微电网的主体,EV为从体的非合作博弈模型,采用粒子群优化算法对模型进行求解;通过典型算例验证所提方法的有效性,以期为电动汽车并网高效率运行提供参考。
1 含电动汽车的风储微电网结构
图1为含电动汽车的微电网系统示意图。微电网以新能源风电供电为主,配置了储能系统用来平抑功率波动,含有柴油发电机作为备用电源,同时并入配电网进行能量交互满足系统功率平衡。EV通过V2G技术并网,与微电网进行充放电功率交互。
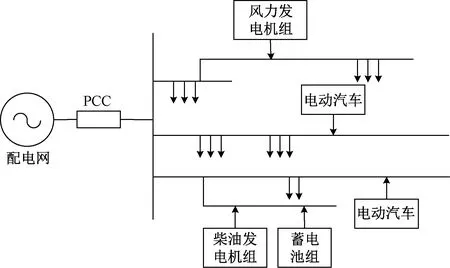
公共连接点(point of common coupling,PCC)
2 分档电价模型
针对分时电价激励可能导致EV响应堆积和实时电价(real-time pricing,RTP)激励可能导致EV响应疲惫及产生新的负荷尖峰比的问题,考虑介于分时电价和实时电价之间的分档电价激励策略,期望实现电动汽车的适度响应,以获得好的调峰效果。分档电价是一种基于RTP和倾斜分档率(incliming block rates,IBR)的电价机制,在每一个调度时段,以该时段的实时电价为基础,根据净负荷大小分成多个档位电价,对不同净负荷大小实施不同的激励电价,期望达到EV适度响应的目的。
系统根据等效净负荷大小制定其RTP,可表示为
Ln,t=PD,t+PEV,t-PWT,t
(1)
RTPt=atLn,t+bt
(2)
式中:Ln,t为t时段的微电网系统净负荷;PD,t为系统的常规负荷;PEV,t为EV集群的充放电功率(正值表示充电,负值表示放电);PWT,t为t时段的风力发电功率;at、bt为RTP设置参数,可根据不同时段用户需求设定;RTPt为t时段下RTP数值。
基于RTP和IBR机制,制定如下分档电价。考虑IBR设定以下多种电价等级为
(3)
式(3)中:η1、η2、η3、η4为净负荷大小临界值,将其划分为多个区间用于制定不同等级的分档电价;At、Bt、Ct、Dt、Et、Ft分别为6个不同电价等级下的电价,可表示为
(4)
式(4)中:α1、α2、β1、β2、β3为不同等级下的价格倍率,且满足α2>α1>1,β1>β2>β3>1。
可得分档电价LP(Ln,t)为
(5)
图2为LP(Ln,t)分档电价机制示意图。由图2可知,具体电价与等效净负荷Ln,t有关。当Ln,t≥0时,微电网实施LP(Ln,t)购电电价,会随着Ln,t增加而增大,当超过阈值η1、η2后,LP(Ln,t)会迅速提高,鼓励更多EV用户参与调度进行放电,用户考虑价格因素后EV会适当增大放电安排而抑制充电需求;当Ln,t<0时,微电网实施LP(Ln,t)售电电价,并随着Ln,t减少而减小,当超过阈值-η1、-η2时,LP(Ln,t)会迅速降低,鼓励更多用户充电,用户考虑价格因素后会适当抑制EV放电需求。
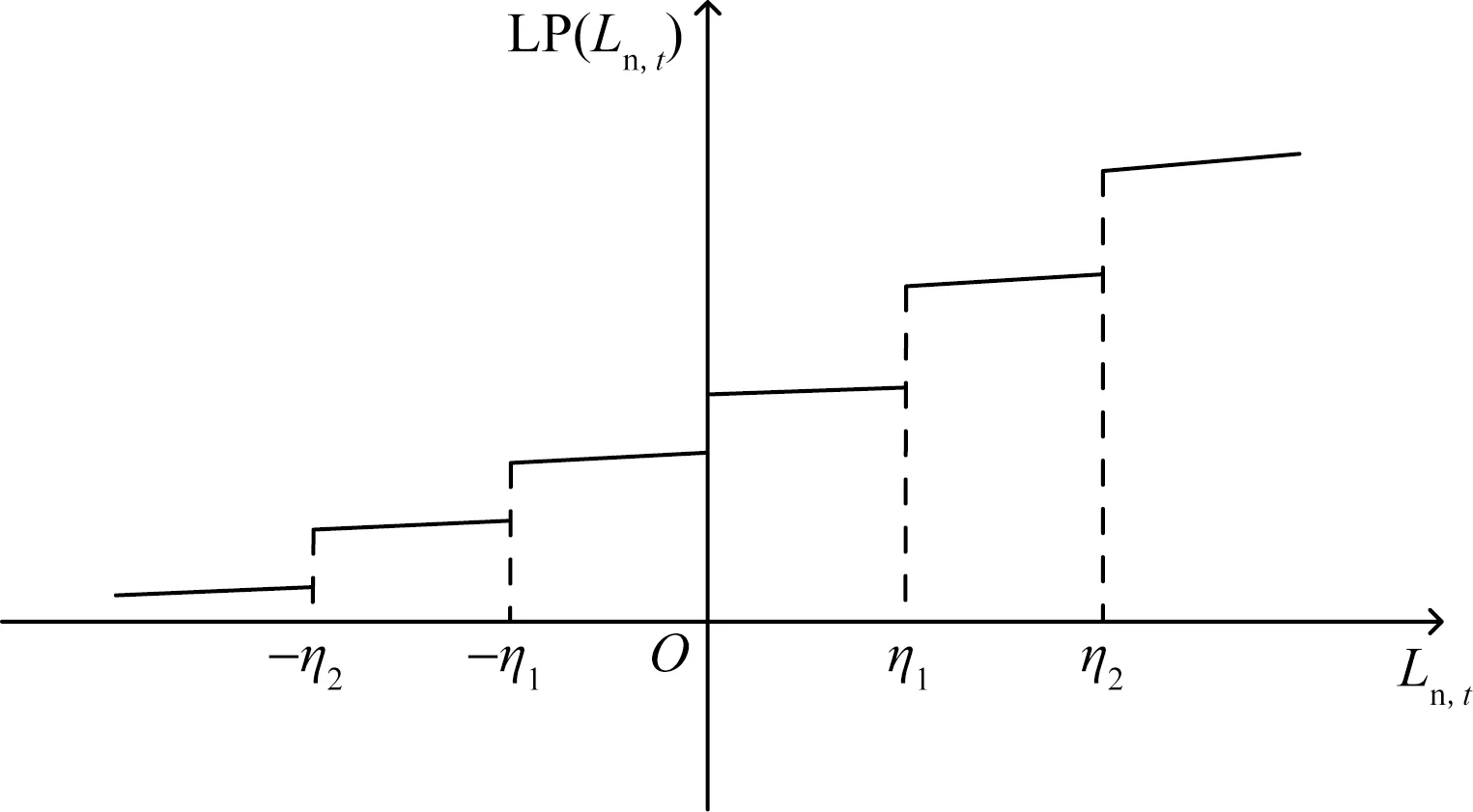
图2 分档电价机制关系
如式(1)和式(5)所示,在EV参与调峰过程中,随着EV响应力度的不同,微电网净负荷Ln,t会随着变化,Ln,t落入不同的档位,对应的电价不同,反过来影响调整EV的响应力度,以达到EV适度响应的目的。
3 考虑碳排放的含电动汽车微电网的成本模型
3.1 成本模型
(1)电源投资成本CS与电池老化费用Ca可分别表示为
(6)
(7)
式中:n为微源种类;ci为第i种微源的单位投资成本系数;PE,i为第i种微源的额定功率;a为折现利率,取8%;γ为使用年限,通常取20年[17];fa、z、SH分别为电池的单位成本、损失系数与报废容量;St、St+1为t、t+1时刻电池的电量。
(2)微电网可控机组发电成本。可控机组柴油发电机的发电成本可以分为燃料成本CDE,t与治污成本CP,可分别表示为
(8)
(9)
式中:PDE,t为柴油机机组t时刻下的输出功率;a、b、c为成本系数;αk、βk分别为治污成本系数与污染物排放量。
(3)微电网各微源运行维护成本Cm可表示为
(10)
式(10)中:cm,i为第i种微源维护成本系数;Pm,i为第i种微源的日发电功率。
(4)新能源补贴。
(11)
(12)
式中:Cwtbt、Cevbt分别为新能源发电补贴与EV放电补贴;Cb为EV放电补贴电价;Cwt为风电补贴电价。
3.2 碳配额交易模型
碳交易机制是一种能够实现解决以二氧化碳为代表的温室气体减排问题的市场化机制,即把碳排放权作为商品进行合理分配与买卖交易,能够限制温室气体排放以解决严峻地环境污染等问题。在推动城市经济发展的同时,交通行业的节能减排问题也需引起重视。为了鼓励EV发展并作为主体参与到碳交易市场中发挥其减排效益,考虑将相同行驶距离下EV与传统燃油汽车碳排放量的差值作为其碳排放额,并能够将多余的碳配额放于电力市场出售获得利益。根据目前中国碳交易政策,参与碳交易市场的EV可以获得一定的免费配额,相比于给予传统的新能源补贴,更能够使EV积极参与调度并发挥其节能减排作用[18]。由于免费分配法中基准线法对促进系统性节能减排的目标实现效果更加显著[19],因此采用基准线法进行研究。
柴油机和风机拥有一定的免费配额,其作为微电网侧的配额主要构成部分,若实际发电所需碳配额超过其所获得的免费额度时,需要额外购买缺额部分的碳排放权;若不超过其免费配额时,能够将剩余免费配额向碳交易市场售出获取一定利益。由此,可计算微电网侧的碳交易的成本为
Cc,t=qw(EwPw,t-εPt)
(13)
式(13)中:Cc,t为t时刻机组的碳交易成本,若为正则需购买排放权,若为负则可出售排放权获得收益;Pw,t为t时刻柴油机组和风机的有功出力之和;qw为微电网碳交易配额的价格;Ew为发电机组单位电量排放因子;ε为碳排放配额分配系数;Pt为t时刻发电机组的免费配额。
EV侧通过将其充放电功率转换为碳配额作为补贴,再将其通过电力市场出售碳配额获取部分收益。根据研究表明:传统燃油汽车行驶单位距离所产生的碳排放量与EV采用柴油发电机充电行驶单位距离所产生的碳排放量基本相同[20]。
由此,可以计算EV侧碳交易的收益为
Cev,t=qev(Mev1,t-Mev2,t)
(14)
Mev1,t=PEV,tΔtLevEgas
(15)
(16)
式中:Cev,t为EV在t时刻出售碳配额获得的收益;qev为EV碳配额售价;Mev1,t为t时段与EV总充电量可供行驶相同距离的燃油汽车行驶产生的碳排放量;Mev2,t为t时段EV充电所对应的柴油发电机碳排放量;Δt为每一时段,数值取1;Lev为EV单位电量可行驶的距离;Egas为燃油汽车行驶百公里产生的碳排放量。
4 分档电价和碳配额激励的含电动汽车微电网博弈优化调度策略
对于含电动汽车的微电网来说,将微电网与电动汽车分为两个主体,微电网优化目标是在满足系统功率平衡的前提下,实施合理有效的激励措施,鼓励EV有序化参与其削峰填谷调度,实现运行经济效益最大与EV充放电后等效负荷均方差最低。EV响应微电网的激励政策,以运行经济性效益最大为目标。
4.1 含EV微电网电力调度分析
微电网中的负荷曲线PD,t、风电出力曲线PWT,t均具有波动性和随机性,且通常峰谷不同步是新能源消纳的主要障碍。微电网的能量调度压力主要出现在源荷平衡后等效负荷曲线的峰谷期,其表达式为
ΔPt=PD,t-PWT,t
(17)
对于含EV的微电网而言,EV的无序接入会加重微电网的调度压力。微电网期望通过激励政策引导EV进行有序充放电,由此可获得有利于平滑ΔPt的调节功率PEV,t。考虑EV充放电后,系统的净负荷可表示为
ΔPt=Ln,t=PD,t-PWT,t+PEV,t
(18)
ΔPt实质上反映了微电网中新能源的供电能力,对于EV参与调度后剩余的功率不平衡量,首先通过储能充放电功率PESS,t进行平抑,其次通过可控机组出力PDE,t与配网功率交互Pgrid,t进行平抑。
ΔPt+PESS,t-PDE,t-Pgrid,t=0
(19)
式(19)中:Pgrid,t为t时刻微电网与大电网的交互功率。
微电网ΔPt越平滑(峰谷差越小和波动越小),越能减轻微电网储能、可控机组以及与电网交互功率的调度压力,而其实现则有赖于微电网实施合适的激励政策,以引导EV的适度响应。
4.2 分档电价和碳配额激励思想
微电网根据其等效净负荷设定的分档电价机制和碳配额分配政策,激发EV通过有序充放电参与微电网调度,期望达到对等效负荷曲线ΔPt更好的“削峰填谷”效果。
4.2.1 分档电价激励
如2.1节中所述,当等效净负荷Ln,t>0时,风电缺额。若购电分档电价越高,说明风电缺额越多,激励更多EV进行放电,以弥补新能源出力不足,减小储能系统和柴油机组供电压力。同理,当Ln,t<0时,风电过剩,若售电分档电价越低说明风电过剩越多,激励更多EV进行充电以消纳风电过剩功率,减小储能压力。
4.2.2 碳配额激励
将碳配额作用于分档电价机制的基础上,进一步实施双重激励政策。微电网对于参与调度的EV可以实施碳配额奖励机制,其奖励思想为:当PWT,t出力不足时,只对放电EV进行碳配额奖励,此时,对于充电EV无奖励,引导EV进行放电弥补新能源出力不足;而当PWT,t出力过剩时,只对充电EV进行碳配额奖励,对于放电EV无奖励,引导EV充电进行新能源消纳。
相比于仅考虑单一电价机制,考虑分档电价与碳配额双重激励政策能够更加有效地提高EV参与微电网调度的响应度。在保证新能源完全消纳的基础上,期望实现更优地“削峰填谷”效果。
4.3 分档电价和碳配额激励的含电动汽车微电网优化调度策略
微电网优先消纳自有新能源后实施分档电价机制和碳配额激励政策,合理引导EV充电放行为实现有序化,同时,EV的响应会影响微电网的能量调度,进而影响激励政策的优化。
首先设定一个初始分档电价,分别计算t时刻等效负荷ΔP(t)、净负荷Ln(t)。根据Ln(t)数值大小所在阈值范围,考虑IBR计算分档电价,期望以微电网中负荷需求引导EV参与调度并进行充放电。此时,将碳配额奖励机制作用于该时段下选择充放电行为的EV,增加激励力度。对于并网型含EV的微电网,当EV优先平衡ΔP(t)后,其次考虑储能系统与可控机组或从配网购售电以达到平衡。图3为含EV微电网优化调度策略流程图。
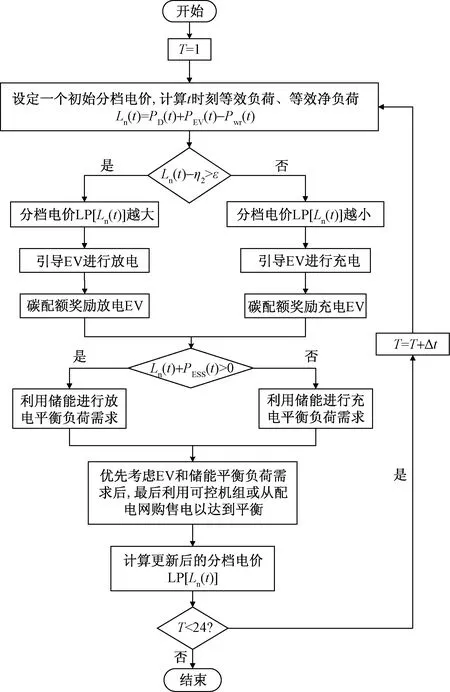
Pwr为风电机组出力
5 含电动汽车微电网优化调度的主从博弈模型
根据所提出的优化调度思想,考虑新能源完全消纳,采用分档电价并结合碳配额制定引导EV参与调度的充放电策略,将微电网侧与EV侧作为不同经营主体,建立主从博弈优化模型。该博弈模型以微电网侧为主体,制定分档电价与碳配额奖励机制,定义微电网分档电价LP(Ln,t)为主体决策变量γ1,优化目标为微电网运行成本和负荷均方差最小;以EV侧为从体,其调度方案为PEV,t为从体决策变量γ2。优化目标为车主成本最小。通过迭代求解博弈优化模型纳什均衡点,获得微电网侧最优分档电价与电网汽车充放电方案的集合。
5.1 微电网侧优化模型
5.1.1 目标函数
考虑微电网侧经济性与EV接入造成负荷波动的影响,采用加权法将其运行成本最小和极小化负荷均方差作为目标函数J1,可表示为
J1=ωμ(J11)+(1-ω)μ(J12)
(20)
J11=Cm+Cs+Cp-Cwtbt+εqw|PEV,t|+
(21)
(22)
(23)
式中:J11为微电网运行成本;J12为微电网负荷均方差;ω为权重系数,取0.6;Pave为等效负荷平均值[21]。
由于式(21)、式(22)两个目标函数的量纲不一致,需采用模糊法对多目标问题进行归一化处理,可表示为
(24)
(25)
式中:μ为微网侧各目标函数进行归一化处理后的数值;J11M与J11m分别为微电网运行成本最大与最小值;J12M与J12m分别为微网侧负荷均方差最大与最小值。
5.1.2 约束条件
(1)柴油机出力上下限约束。
(26)
(2)蓄电池充放电功率约束。蓄电池充放电功率的大小不超过电池容量的20%[21]。
min[Pc,max,(SCmax-SC)Er/ηc)1≤20%Er/ηc
(27)
min[Pd,max,(SC-SCmin)Erηd]1≤20%Erηd
(28)
式中:Pc,max、Pd,max分别为蓄电池充放电功率的上限;SCmax、SCmin为蓄电池最大、最小荷电量;SC为各时段下荷电量数值;Er为蓄电池容量;ηc、ηd分别为蓄电池充、放电效率系数。
(3)联络线功率约束。
(29)
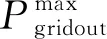
5.2 EV侧优化模型
5.2.1 目标函数
EV用户侧积极响应微电网的激励政策,优化车主的用电成本。其目标函数J2包括电池老化费用、充放电费用、碳配额收益与放电补贴,可表示为
(30)
5.2.2 约束条件
(1)EV充放电功率约束。
(31)
(2)EV充放电总量约束。EV放电总量应小于总放电率,总充电量与EV的行驶需求相关,其为常数且等于充电总量。
(32)
(33)
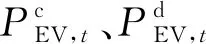
5.3 运行性能评价指标
为了直观表示所提的考虑分档电价与碳配额激励政策引导EV集群参与微电网调度后削峰填谷的效果,除考虑用户与微电网经济性外,列举相对峰荷削减率(relative peak reduction, RPR)指标评价其执行能力,其表达式为
(34)
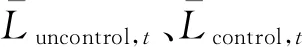
6 基于粒子群算法的优化模型求解
6.1 模型求解
针对所建立的主从博弈模型,采用粒子群智能算法进行求解。该模型可分为内外两层进行求解。内层模块寻优EV侧响应分档电价的最优充放电策略;外层模块旨在优化微电网侧分档电价。内外层反复迭代找寻最优解,当各主体相邻两次迭代的结果误差的绝对值不超过一个极小正数δ时,则认为达到纳什均衡解。博弈求解流程图如图4所示。
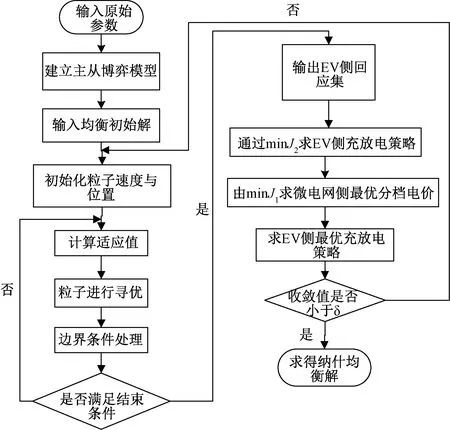
图4 模型求解流程图
6.2 算例分析
6.2.1 参数设置
以某区域含风力和ESS的并网型微电网为例,其中配电网分时电价为:峰时段10:00—14:00电价为1.256元/(kW·h),夜间23:00—次日7:00为低谷电价0.249元/(kW·h),其他时段为平电价0.503元/(kW·h)。ESS容量为3 200 kW·h,荷电状态上、下限分别设定为1和0.2;EV放电补贴Cevbt为0.503元/(kW·h);风力发电补贴Cwt为0.62元/(kW·h);IBR电价阈值η1、η2、η3、η4分别设为200、400、-200、-400 kW;价格倍率α1、α2、β1、β2、β3分别设为1.05、1.15、1.25、1.15、1.05;RTP系数at=0.002、bt=0.2,以EV规模为100辆进行以下分析。
6.2.2 优化结果及其分析
不同场景对EV参与调度的影响微电网的新能源与负荷数据如图5所示。可以看出,考虑风电完全消纳,系统内等效负荷的峰谷时段发生了一定变化。参照的EV无序充电时的负荷曲线(图6)可知,常规负荷需求较少的时段,EV充电量较少;在常规负荷较高的时段,EV也有更多的充电需求。此时若不对EV充放电行为进行合理引导,则会增大微电网侧调度压力。
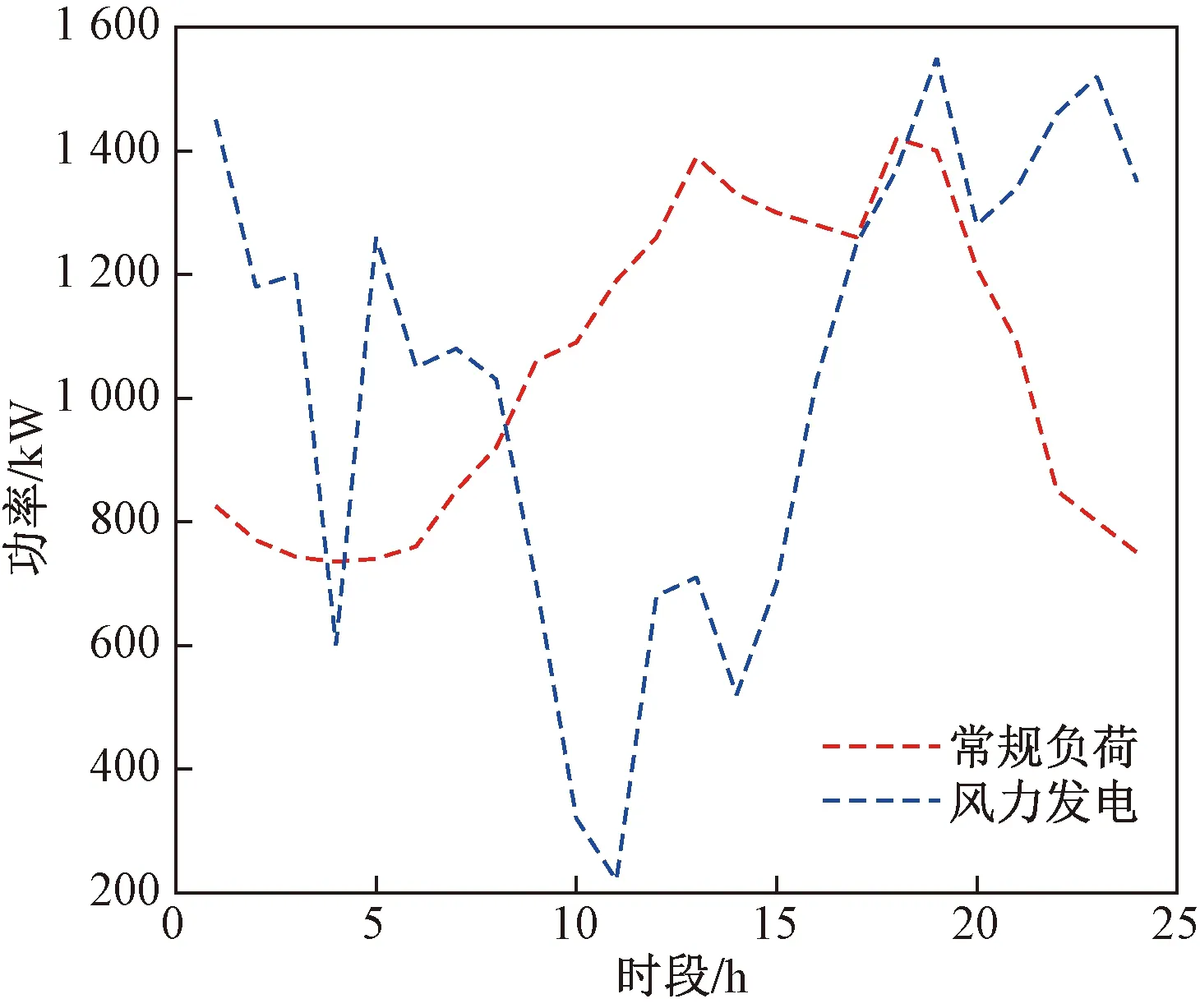
图5 微电网典型日风电出力与负荷预测曲线
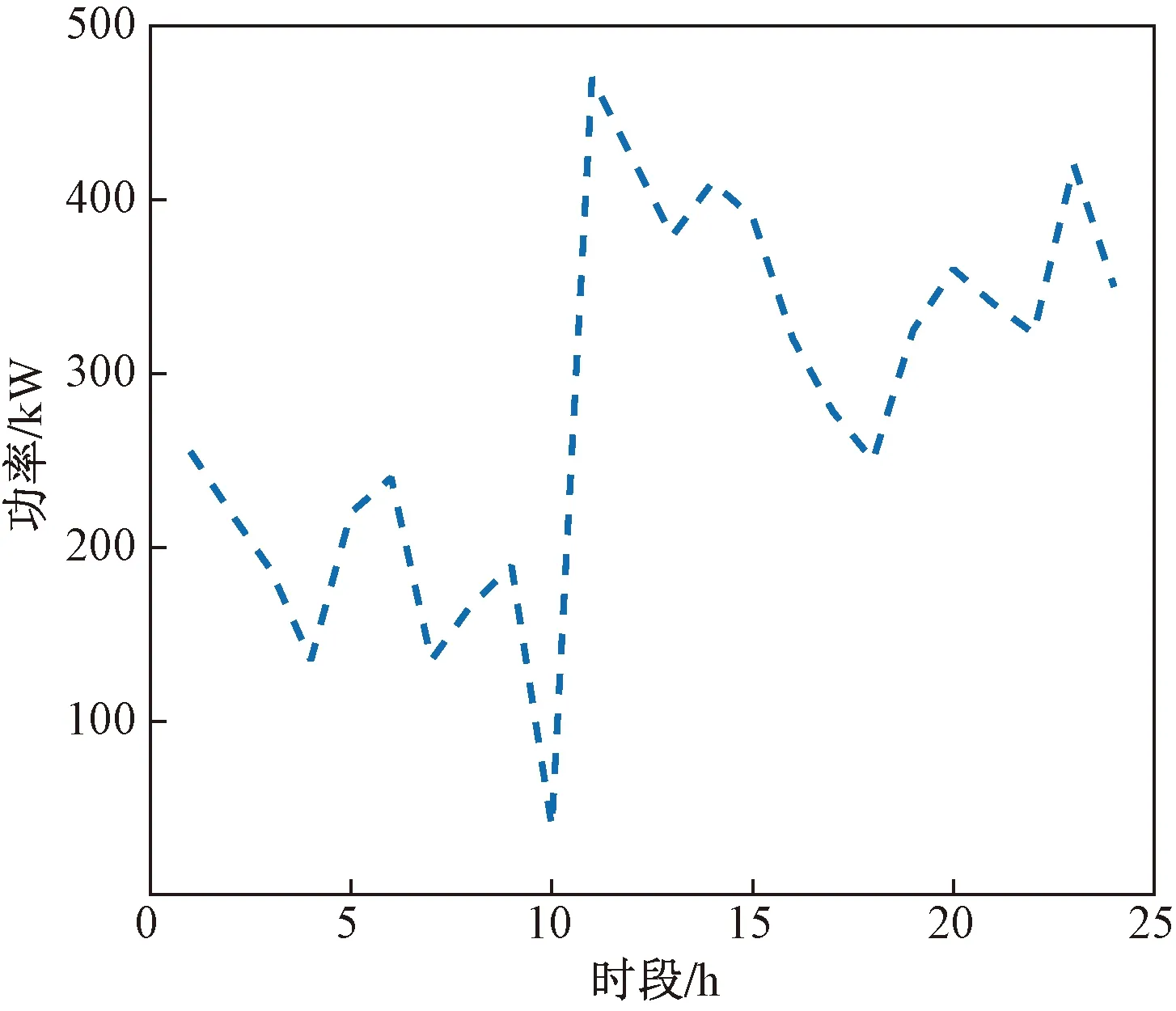
图6 EV无序充电时负荷曲线
在同一微电网中设置了4组场景进行仿真分析,对比不同场景下的EV响应效果。
场景1EV无序充电。
场景2分时电价激励EV有序充放电。
场景3分档电价激励EV有序充放电。
场景4所提双重激励EV有序充放电。
图7为采用主从博弈模型优化得到的考虑EV在不同场景下的等效负荷曲线对比结果。图8~图11为不同场景下EV充放电策略及其对应的等效净负荷曲线,图12为优化后每一时段等效净负荷与其所对应的分档电价。如图9所示,微电网仅实施分时电价激励引导下,在风力过剩而电价低的时段EV充电较多,而在电价高时充电较少,造成了新的峰谷差(图8)。结合图10可知实施分档电价激励政策时能够有效地减少仅由分时电价激励所产生新的峰谷差的现象;由图11可得,在实施双重激励优化策略后,EV用户选择在风电出力多电价低时充电,风电出力不足电价高时进行放电,削峰填谷起到了更优的效果。而当负荷需求过剩且风电出力不足的时段,更多EV积极参与调度并进行放电,有效地减轻了微电网侧供电压力,同时实现了EV作为绿色电源节能减排的效果。结合图12可知,EV在净负荷较大电价高时积极放电,在净负荷较小电价低时积极充电;如图7所示,对比4种场景结果,可以看出,实施双重激励优化策略,能够引导EV的适度响应,更优地改善微电网等效负荷曲线,使曲线更加平缓,有利于减轻微电网储能及可控机组的调度压力。
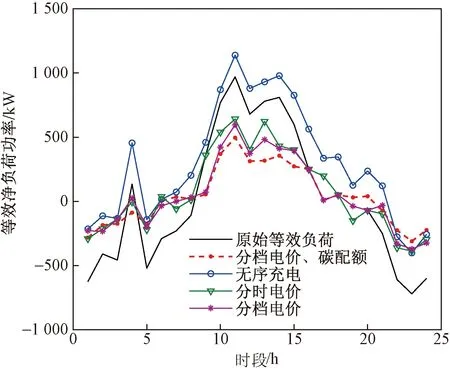
图7 考虑EV在不同场景下的等效负荷曲线对比
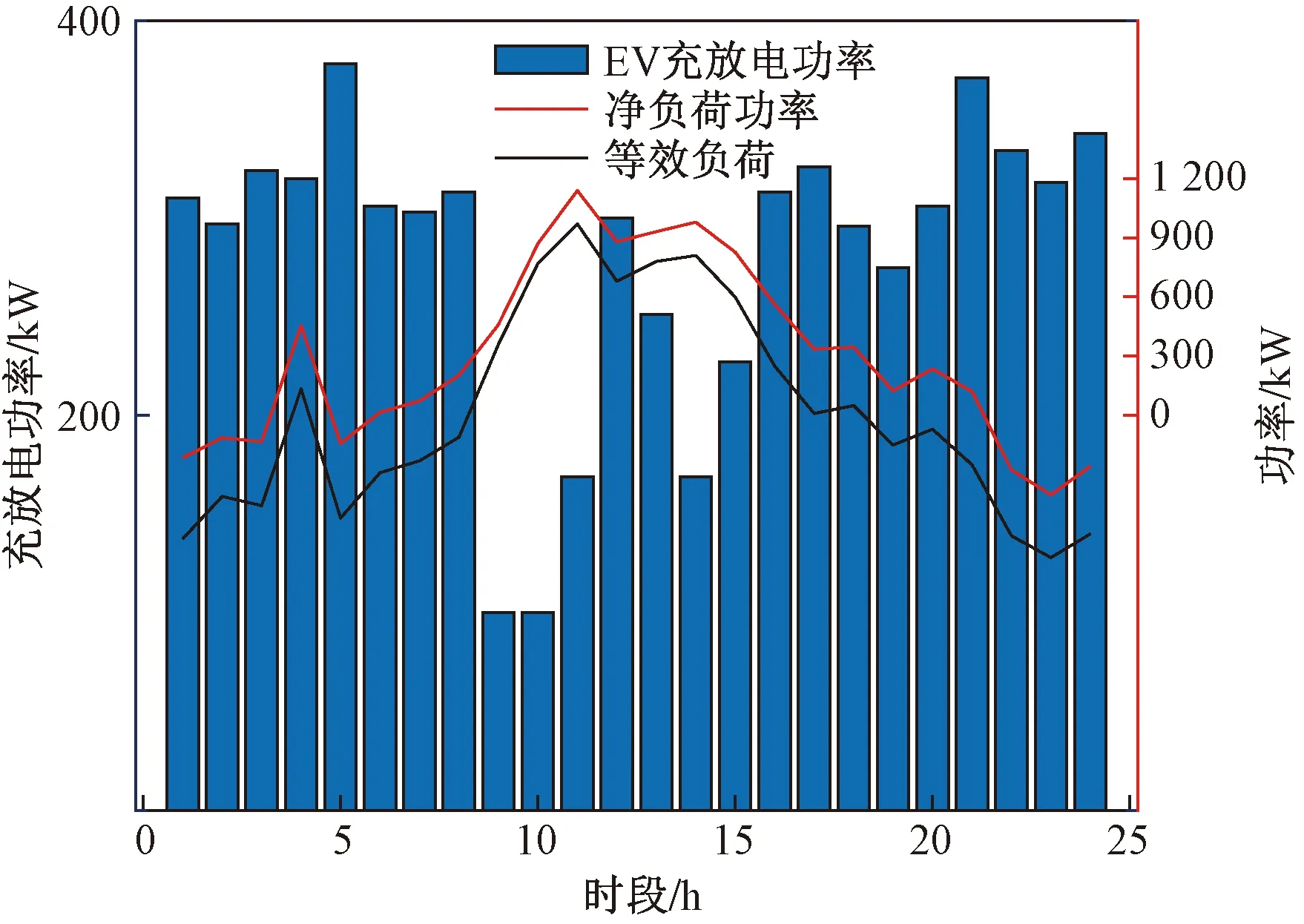
图8 无序充电场景下的EV充放电策略及其净负荷曲线
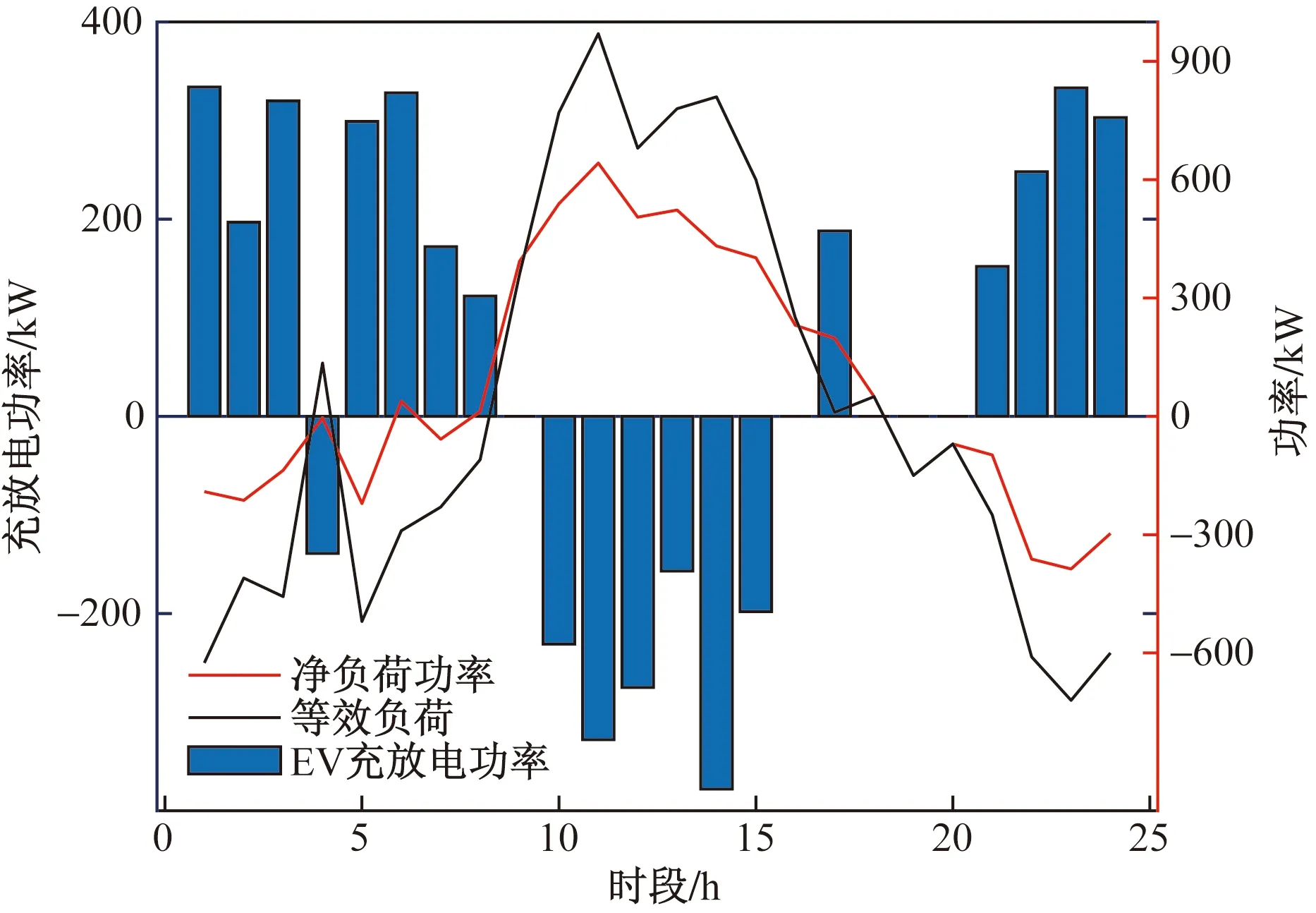
图9 分时电价引导下的EV充放电策略及其净负荷曲线
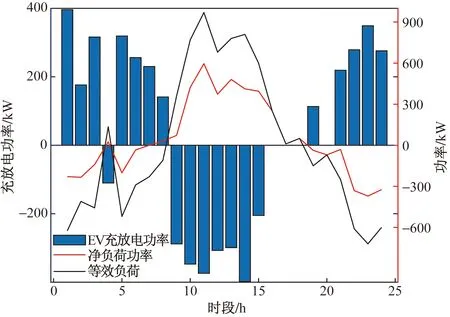
图10 分档电价引导下的EV充放电策略及其净负荷曲线
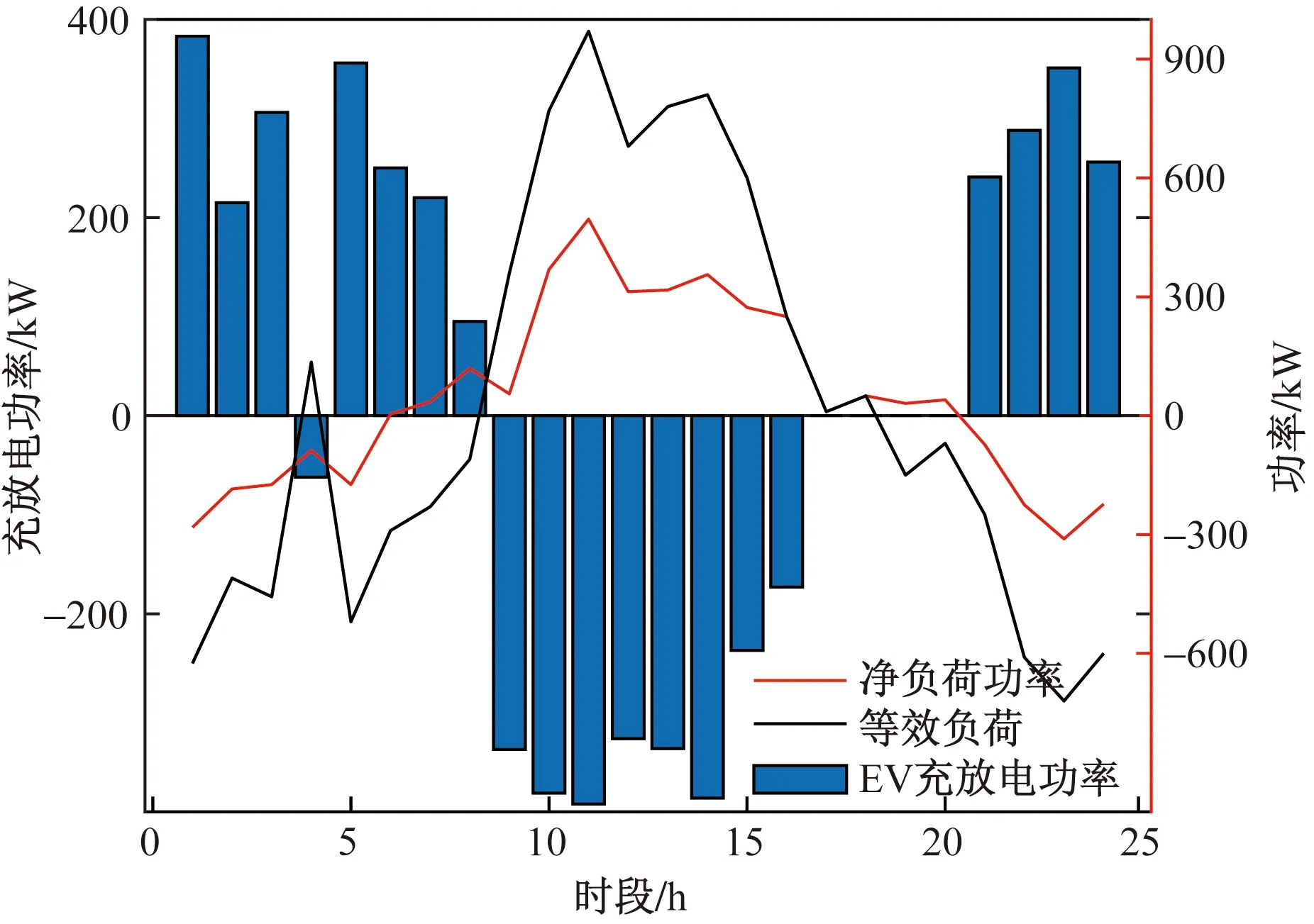
图11 所提激励引导下的优化后EV充放电功率及其净负荷曲线
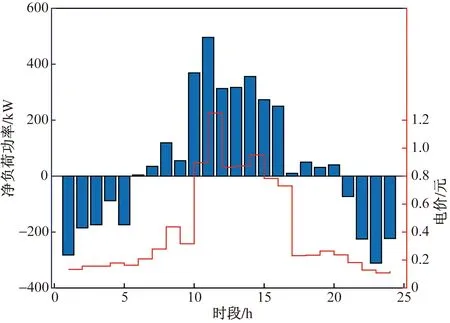
图12 优化后的净负荷与所对应分档电价的数值
表1为不同场景下优化后的相关结果的统计数据。可以看出,由于在分时电价下EV仅单纯倾向于在电价高时放电、低谷时充电,但峰谷各时段内的激励效果无差异,有失灵活性,调峰效果相对较差。而引入分档电价与碳配额激励政策后,其优化后峰谷差率比仅考虑分时电价场景下降低8.13%,实现了更优的削峰填谷效果。
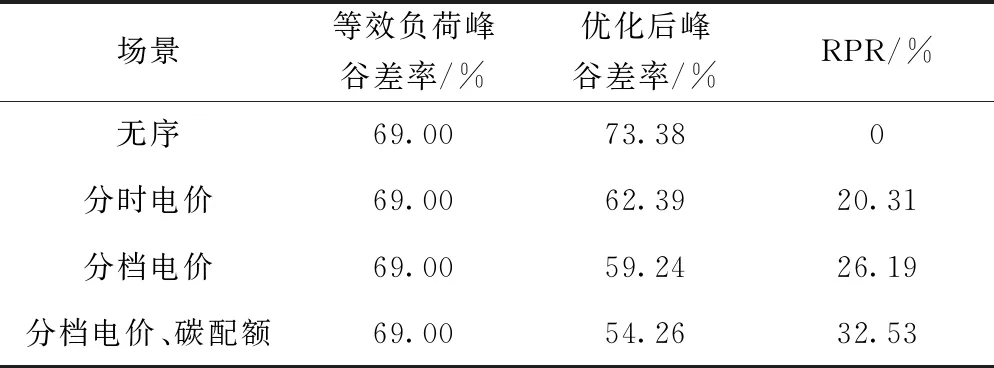
表1 不同场景下优化后的相关统计数据
由表2能够看出,实施碳排放配额激励政策后,微电网侧与EV侧将多余的碳配额转化为自身收益,微电网侧收益增加460.2元,而EV侧经济效益增长更为明显,增加了1 016.8元。

表2 微电网侧和EV侧成本比较
6.2.3 EV集群规模对优化结果的影响
为了研究EV数量对参与微电网调度的影响,设置了3组不同规模大小的EV集群进行仿真结果比较,其EV集群规模中分别含有100、150、200辆的EV参与调度。3组EV集群规模下削峰填谷曲线对比如图13所示。
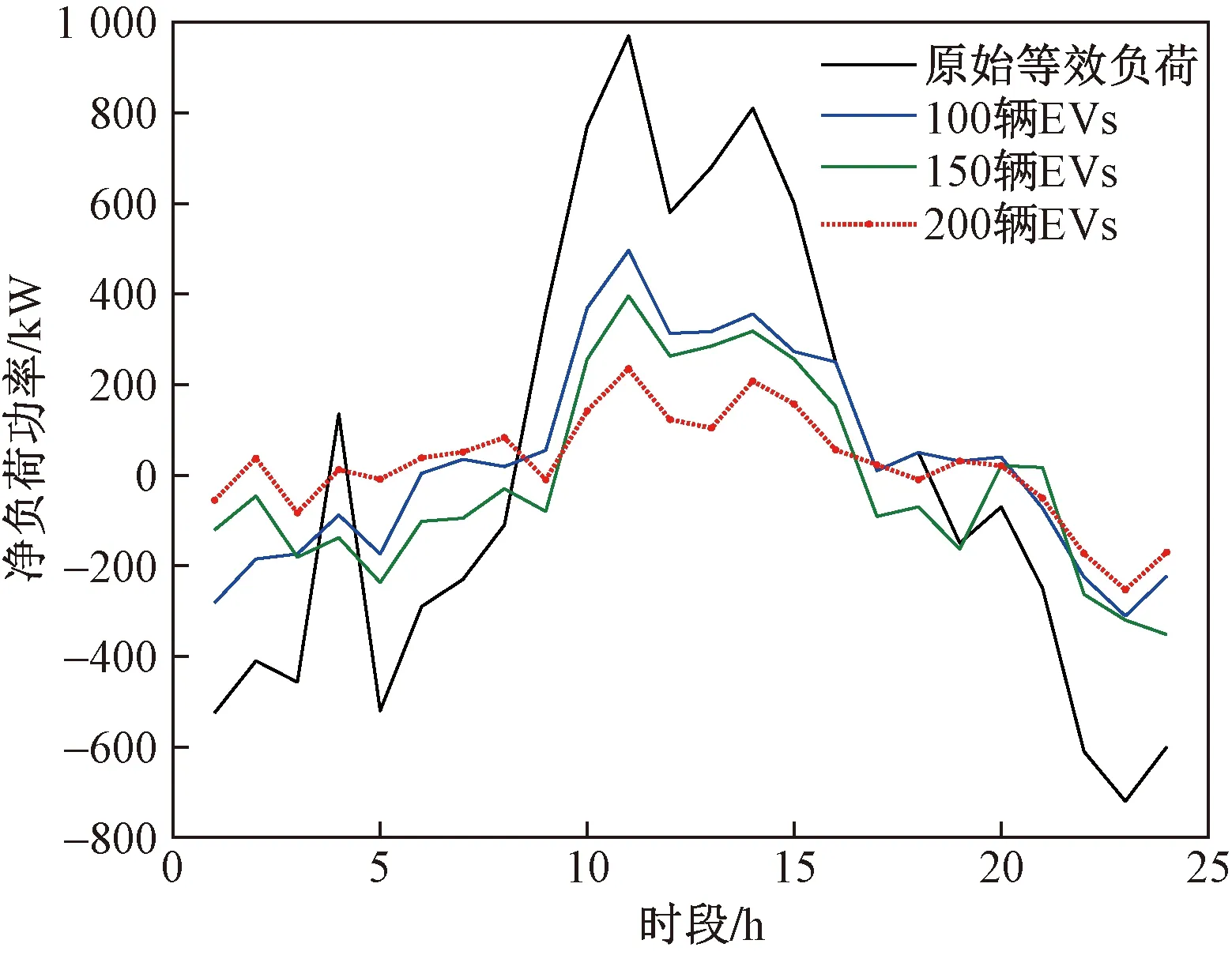
图13 不同EV集群规模比较曲线图
由表3可以看出,随着EV数量增多,参与调度后的净负荷曲线峰谷差率逐渐减小,相对负荷削减率 RPR逐步提高。因此,EV集群规模的合理增大能够有效提升需求侧响应能力,即其削峰填谷效果越好。
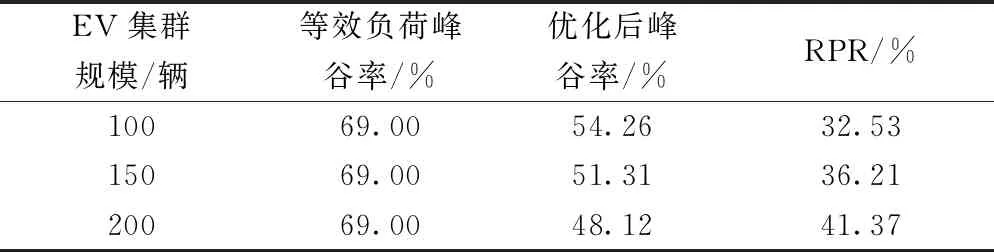
表3 同EV集群规模下所提模型相关统计数据
7 结论
考虑新能源完全消纳,基于RTP和倾斜分档率机制,提出了一种分档电价机制。结合分档电价和碳配额激励政策,建立了主从博弈优化调度模型,利用粒子群算法求解优化模型纳什均衡点。通过算例仿真分析,得到如下结论。
(1)微电网采用分档电价与碳配额激励政策能够引导优化EV充放电行为的适度响应,以改善微电网负荷特性。
(2)所建立的优化模型能够同时满足微电网侧运行成本最小和极小化负荷均方差,EV用户侧成本最小目标。能够在考虑碳配额后通过博弈优化后使两侧效益最大化以达到共赢效果。
(3)所提的调度策略随着EV集群规模合理地增大,可以有效提升EV的响应能力,达到更优地削峰填谷的效果,以适应未来EV大规模发展。
