基于MeanShift 的短波跳频信号快速盲检测

朱政宇，林宇，王梓晅，巩克现，陈鹏飞，王忠勇，梁静,3

（1.郑州大学电气与信息工程学院，河南 郑州 450001；2.郑州大学电子材料与系统国际联合研究中心，河南 郑州 450001；3.河南省智能网络和数据分析国际联合实验室，河南 郑州 450001）

0 引言

跳频（FH,frequency hopping）通信作为一种特殊的扩频通信方式，信号载波频率能够按照一定规律随机跳变，具备优越的抗衰落、抗干扰和抗截获能力。随着跳频通信技术在短波频段的应用，从复杂的短波信道环境中检测跳频信号，成为进行跳频信号参数估计和网台分选的前提和基础[1]。

由于短波信道环境异常复杂，定频、突发等各种信号相互交织、分布密集，且环境噪声起伏大，严重影响了短波信道环境下的跳频信号在低信噪比下的检测性能[1]。迄今为止，跳频信号检测的研究方向大致分为盲检测与非盲检测两类。在未知的信道环境中以及无任何先验信息的情况下，为了实现对跳频信号的实时捕获和处理，跳频信号的实时盲检测具有重要意义。文献[2]利用短波信号能量谱特征的差异，提出了一种基于频谱能量统计的短波信号检测算法，但在低信噪比下检测效果较差。文献[3-4]提出一种基于频谱灰度形态学滤波算法，降低短波信号检测中噪底起伏大、干扰信号多的影响。文献[5]提出基于短时傅里叶变换（STFT,short-term Fourier transform）的信道化结构，方法简单，但仅基于信号功率检测，在低信噪比下检测效果将会骤降。对接收信号进行信道化处理后对每个子信道信号进行自相关处理，实现跳频信号检测，一旦跳频信号跨信道，就会丢失跳频的某一跳（Hop），导致检测概率下降[6]。文献[7]利用滑窗重叠滑动生成时频图，提高时频域分辨率，提高信号检测概率。文献[8]在短波信道下，推导出检测概率与虚警概率的理论闭式解，结合最小化误差概率方法得到最优门限以提升检测概率。文献[9]将一种新的宽带转换器重构算法应用于检测跳频信号，使跳频信号可以被彻底重构，却未考虑存在干扰信号环境。文献[10]通过短时能量对消的方法来检测每个子信道跳频信号的存在性，但没有考虑跳频信号跨信道问题。文献[11]为消除干扰信号的影响，设置局部自适应阈值，实现跳频信号的提取，但在短波信道下检测性能和抗干扰能力较差。基于神经网络方法减少了频谱泄露和时频分辨率差的影响来提升检测性能，但计算复杂度高[12]。文献[13]在信号频域引入导频，利用导频与信号的互相关收集光谱泄露的能量，提高信号检测概率，但计算复杂度较高且在强干扰环境下检测概率急剧下降。文献[14]提出一种跳频信号的非合作压缩检测方法，与随机测量核相比，该研究利用信号分布的先验知识设计测量核，提高检测性能，但对硬件要求高。文献[15]利用支持向量机对跳频信号和干扰信号进行分类，实现跳频信号的检测，但计算复杂度较高。文献[16]利用平滑伪Wigner-Ville 分布（SPWVD,smooth pseudo Wigner-Ville distribution）生成时频图增加了时频计算量，不利于工程实现。以上方法均属于非盲检测范畴，须提前预知观测信号和跳频信号的频率集或跳速，但在实际工程中难以获取任何先验知识，因此无法实现跳频信号的非盲检测。

针对基于功率谱对消方法[17-18]，文献[19]提出了时频对消比方法，可以在较低信噪比下检测出跳频信号，但在复杂的电磁环境下，未进行预处理，判决门限易出错导致漏检跳频信号。针对传统二值化形态学滤波算法门限不易选取的问题，文献[20]提出了一种基于二次灰度形态学滤波算法，能够正确选取二值化门限，但该方法易导致定频信号多处断开，误判为突发干扰信号，导致虚警概率上升。基于K-Means 聚类的跳频阈值分割算法[21]和基于改进K-Means 的特征集分类算法[22-23]均能在低信噪比下提取跳频信号，均有较高的检测概率，但K-Means 聚类算法需要预设类簇个数，在短波信道下抗干扰能力较弱。文献[24]利用短波跳频信号的纹理特征，通过灰度共生矩阵生成信号纹理图，实现跳频信号盲检测，但以增加计算复杂度克服阈值分割的不足。文献[25]采用小波分解与希尔伯特-黄变换提高了跳频信号检测的精度，但在短波复杂的电磁环境中，检测效果受限于小波基的选取。以上方法均在无任何先验信息的条件下完成跳频信号的检测，属于盲检测范畴，但均有计算复杂度高、抗干扰能力弱或低信噪比下检测性能差的缺点，在实际工程上难以发挥作用。

综上所述，为了实现跳频信号的快速盲检测，本文结合时频分析技术，在低信噪比下提出一种基于MeanShift 算法的连通域标记跳频信号快速盲检测算法，通过对各信号在连通域上的最大持续时长进行聚类分析，降低干扰信号和尖锐噪声对跳频信号检测的影响。该盲检测算法可应用于同时存在噪声、突发干扰信号、定频干扰信号和扫频干扰信号的短波环境，具有较好的抗干扰能力和检测性能。

1 信号预处理

1.1 信号数学模型

在一定的观测时间内，假设接收机在短波频段内接收到的信号模型为

其中，k≥ 1,l≥ 1,j≥ 1，r(t)为接收的短波宽带信号，sFH(t)为跳频信号，d k(t)为第k个定频干扰信号，cl(t)为第l个扫频干扰信号，e j(t)为第j个突发干扰信号，n(t)为均值为0、方差为σ2的加性白高斯噪声。

假设跳频信号sFH(t)的跳频周期为Th，信号幅度为A，矩形窗为rectTh，且满足

因此，根据文献[20]，跳频信号的接收模型表达式为

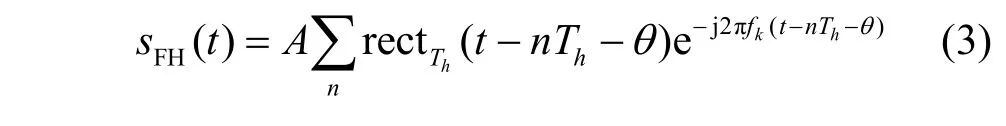
其中，θ表示初始相位，fn表示第n个时隙的跳频频率。

1.2 时频分析

跳频信号的频率随时间呈现不规律变化，属于典型的非平稳信号，在时域和频域上均难以全面地分析此类信号，因此为更有效地检测跳频信号，常采用时频分析技术进行分析处理。目前时频分析的方法主要有STFT[26]、Wigner-Ville 分布（WVD,Wigner-Ville distribution）及其衍生变换[23,25]、各种联合时频变换[23]和小波变换[25]等。

短波宽带信号r(t)的STFT 定义为

其中，h(t)为窗函数，τ为时延，STFTr(t,f)为混合信号r(t)时间和频率上的连续二维分布，其基本思想是将时域信号划分成多个子时域信号段，并加窗处理，分别计算每个子时域信号段的傅里叶变换，因此STFT 是一种线性变换，在使用中不会产生交叉项，计算复杂度较低。

短波信号r(t)的WVD 定义为

其中，τ为时延，Wr(t,f)为短波宽带信号r(t)在t时刻的 WVD。WsFH(t,f)、Wdk(t,f)、Wcl(t,f)、Wej(t,f)分别为跳频信号、定频干扰信号、扫频干扰信号和突发干扰信号的信号项，其余项皆为信号分量之间的交叉项。由式(5)可知，由于r(t)是多分量信号，在WVD 进行双线性变换过程中将产生不同信号分量的交叉项，不利于信号检测。各种联合时频变换虽能抑制交叉项和提高分辨率，但计算复杂度较高，不利于工程实现。为了满足工程需求，本文采用STFT 作为时频分析工具。

2 基于MeanShift 聚类的连通域标记跳频信号快速盲检测算法

2.1 基于时频图的形态学滤波预处理

为了在低信噪比下降低干扰信号的影响，实现跳频信号提取，本文对时频图进行二次灰度形态学滤波处理，即分别在时频矩阵的频率分量和时间分量上进行灰度形态学滤波[20]。预处理流程如下。

1) 在时频矩阵的频谱分量上选择长宽都小于跳频Hop 的线性结构元素对时频图进行腐蚀运算，去除雾状噪声、突发干扰信号和扫频干扰信号。

2) 选择长度略小于跳频Hop 的线性结构元素对时频图进行膨胀运算，使剩余信号恢复原状。

3) 在时频矩阵的时间分量上，使用长宽接近信号带宽的结构元素先进行灰度闭运算再做底帽运算，并求其最大值，此时能够跟踪填补频谱中波谷的极大值，再和灰度开运算的结果相加，可以很好地跟踪噪声，得到二值化门限。

4) 以该门限为最佳阈值，进行二值化分割，使信号灰度为1，背景噪声灰度为0，得到只含有跳频信号和定频干扰信号的二值时频矩阵。

2.2 基于行程的连通域标记算法

为了更有效地去除定频干扰信号且不会造成多余的突发干扰信号，对每一个信号进行8 邻域搜索，属于同一信号的连通起来，并赋予各自的标记。为了降低复杂度并快速标记，采用基于行程的标记算法，在遍历二值时频图像的过程中，记录每一个团（连续为1 的序列）的位置，同时对其8 邻域进行搜索，存在值则送到元组pair 中，再对pair 中每个数据对重新标记[24]。算法流程如下。

1) 遍历时频图，把连续等于1 的白色像素组成的序列称为团，并记下它的起止位置。

2) 依据团的起止位置，若当前团和前一个团之间不满足8 邻域关系，则给当前团赋一个新的标号labelk,k=1,2,3…；反之，则将前一个团的标号赋给当前团；若它与前2 个及以上的团满足8 邻域关系，则给当前团赋上相连团中的最小标号，即min(labeli,labelj,labelh,…),i=1,2,…,i＜j,j＜h并与之前几个团的标记写入数据对(uk,vk),k=1,2,…，存储到pair中说明属于同一类。

3) 将数据对(uk,vk),k=1,2,…转换为序列[u1,v1;u2,v2;u3,v3,… ]，因为它们满足8 邻域关系，所以一个序列的标号相同，从1 开始递增，给每个序列赋一个标号。

4) 在时频图上对团进行标记，重复步骤2)和步骤3)，直至遍历完整个时频图。

2.3 MeanShift 算法

MeanShift 算法假设不同簇类的数据集符合不同的概率密度分布，通过寻找样本集中最密集的方向，并不断偏移到密度最大处，随着样本收敛于局部密度极大值，认为迭代过程中收敛到同一极大值的点是同一簇类的成员[27]。

MeanShift 向量的基本形式定义为

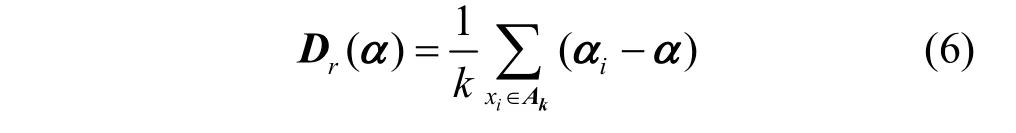
其中，Ak是一个半径为r的高维球区域，α是当前区域的质心，αi是第i个区域的质心，满足以下关系的β点集合

其中，k表示在这n个样本点αi中有k个点落入Ak区域中。这个区域以圆心为起点，其余的点为终点形成不同梯度方向的距离向量。将区域内的距离向量相加，结果就是MeanShift 向量。Dr(α)作为α的偏移均值向量，可用来对α进行更新，在更新过程中可以发现其倾向于向有效区域中样本密度高的地方移动。

为了增强MeanShift 的适用范围，对MeanShift向量进行改进，加入高斯核函数，故改进后的统一表达式为

其中，S(·) 为高斯核函数，r为半径，ω(αi)为样本权重。

MeanShift 的改进形式均由概率密度的核函数估计推导得到，其核心是核函数，故其核函数估计表示为

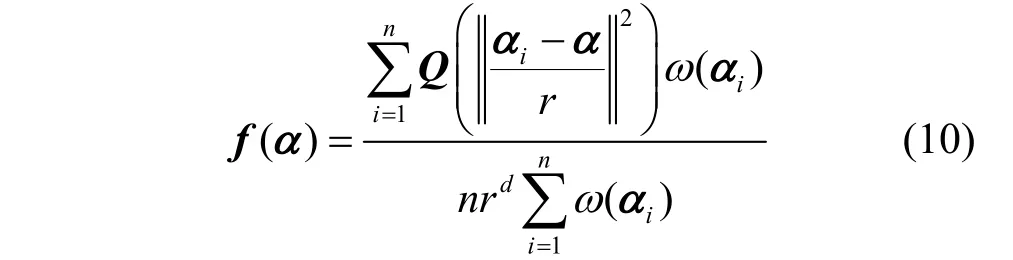
其中，n表示d维数据集{αi}的大小，rd表示d维空间的体积，Q(·) 表示核函数。对概率密度函数f(α)求导如下

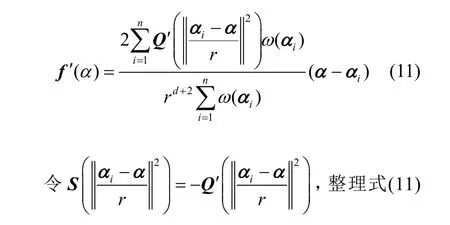
可得

从式（13）可知，f g(α)表示概率密度的核函数估计，D r(α)为MeanShift 的改进表达式。

令 ∇f(α)=0，求解概率密度局部极大值，由于f g(α) ＞0，故有

MeanShift 的本质是求解概率密度局部极大值，即偏移均值向量让目标点始终向概率密度极大点处移动。故常选目标点α附近的一个区域，进行贪心迭代，逐步收敛于概率密度极大值处。

2.4 跳频信号快速盲检测算法原理

本文在无任何先验信息的情况下，利用STFT降低时频运算量，快速生成时频图。采用基于行程的连通域标记算法，一次遍历便完成对时频图信号的标记，减少了标记时间，使每个信号均有专属的特定标号。各连通域的最小行数(coli)min和最大行数(coli)max，计算连通域的最大持续时长

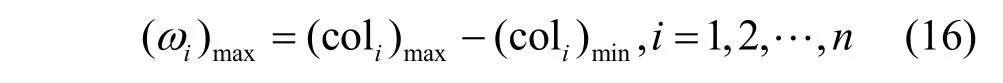
其中，n为标记的信号个数。

将信号的最大持续时长作为数据集，采用MeanShift 算法对该数据集进行聚类处理，减少了数据集的个数，极大地减少了贪心迭代的次数。聚类处理后将时频图中的跳频信号聚类标号均置1，其余标号均置0，对标记矩阵与原始时频图矩阵做哈达玛积运算，即可得到跳频信号的短时能量图，提取出跳频信号。MeanShift 聚类流程如图1 所示。

图1 MeanShift 聚类流程

跳频信号快速盲检测流程如图2 所示。由图2可知，首先对输入的信号数据进行STFT 生成时频图；其次对时频图进行二次灰度形态学滤波去除尖锐雾状噪声、突发干扰信号和扫频干扰信号；再次进行二值化分割，将剩余的跳频信号、定频干扰信号置1，背景置0；然后对二值时频图进行连通域标记，提取出特征标记的最大行数差，即最大持续时长；最后采用MeanShift 算法对信号的最大持续时长数据集进行聚类处理。

图2 跳频信号快速盲检测流程

由于定频干扰信号的频率恒定不变，在时频图的观测时间内为一条连续长直线，若center≈T0，则初判该簇类为定频干扰信号类。跳频信号的频点随着时间变化不断发生不规律跳变，在时频图上为一些长度相等的短横线且对应频率均不一样，跳频信号Hop 在时间上相互衔接。若centerncenter≈T0，则初判该簇类为跳频信号类。突发干扰信号随机出现，且出现的时间很短，在时频图上表现为比跳频信号还要短的短横线，这些短横线的长度可以不一样，且在时间上不衔接。若centerncenter≪T0，则初判该簇类为突发干扰信号类。其中，center 为簇类质心，ncenter为簇类内的数据个数。利用簇类质心与观测时间的关系做初判决，由于预处理后信号的最大持续时长会略有不同，因此需要设置自适应双门限做二次判决，适当提高跳频信号盲检测的兼容性。

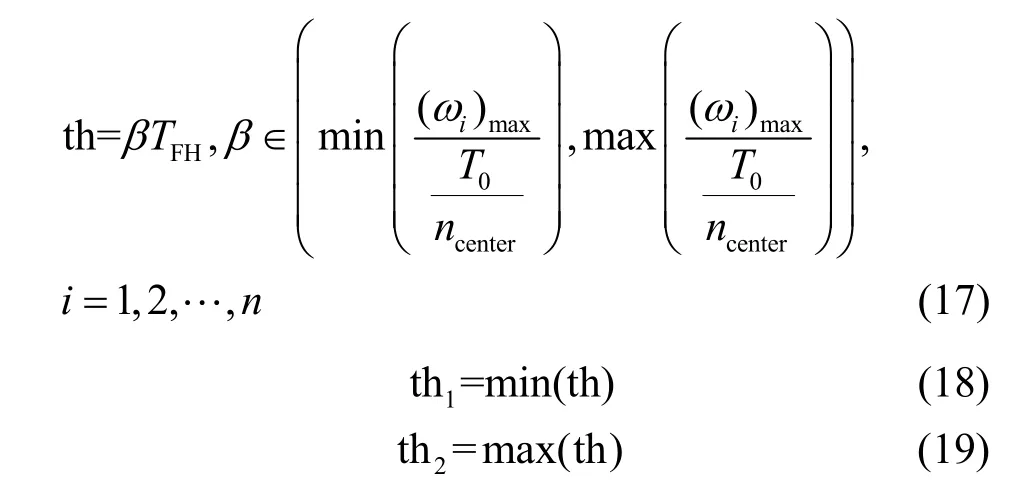
其中，β为自适应因子，T0为观测时间，TFH为初判决中判定为跳频信号类的簇类质心，(ωi)max为信号的最大持续时长，th1为th 最小值，th2为th 最大值。对(ωi)max进行二次判决，若(ωi)max＜ th1，判定为突发干扰信号，标记置0；若th1≤(ωi)max≤th2，判定为跳频信号，标记均置1；若(ωi)max＞th2，判定为定频干扰信号，标记同样置0[24]。

3 仿真实验与分析

假设接收的混合信号包含跳频信号、扫频干扰信号、突发干扰信号、定频干扰信号和高斯白噪声，采样率为10 MHz，观测时间为4 s，跳频信号1 的周期为0.5 s，跳频频率集为[0.25,1,1.25,0.75,1.75,1.5,2,0.5]MHz；跳频信号2 的周期为0.8 s，跳频频率集为[3.5,2.5,4.0,3.0,4.5]MHz；扫频干扰信号的起始频率为3 MHz，截止频率为4 MHz，突发干扰信号的频率集为[0.1,2.7,2.2,4.2,4.8,1.65]MHz，定频干扰信号的频率集为[2.5,3.8,4.6]MHz；短时傅里叶变换采用长度为2 048 个点的Hamming 窗。

实验1二次灰度形态学滤波

当SNR=10 dB 时，对该接收的混合信号进行STFT 变换，并灰度化得到信道环境的灰度时频图。如图3 所示，跳频信号与干扰信号均以白色像素显示，时频图遍布着雾状噪声，背景噪声为黑色。为了滤除噪声和干扰信号，对该时频图进行二次灰度形态学滤波，如图4 所示，图4 中仅剩下跳频信号与定频干扰信号，其余噪声和干扰信号均被滤除。

图3 信道环境的灰度时频图

图4 二次灰度形态学滤波后的时频图

实验2连通域快速标记与聚类

如图5 所示，低信噪比下二次灰度形态学滤波后的时频图发生了变化，部分强噪声无法完全滤除，误判为突发干扰信号。如图6 所示，依据连通域标记原理[17]，当SNR=5 dB 时，对二次灰度形态学滤波后的时频图进行连通域快速标记。经过连通域标记，以每个信号的最大持续时长为特征，对连通域进行基于MeanShift 算法的最大持续时长聚类，聚类结果如图7 所示。标号1、2、3、5、6、8、9、10 为跳频信号1，标号11、14、15、17、18 为跳频信号2，标号12、16、19 为定频干扰信号，标号4、7、13、20 为突发干扰信号。由图8 可知，跳频信号2、定频干扰信号和突发干扰信号的标号为0，跳频信号1 的标号为1，跳频信号2、突发干扰信号和定频干扰信号已完全从时频图中分离出去，能够提取出跳频信号1。同理，由图9 可知，跳频信号1、突发干扰信号和定频干扰信号已完全从时频图中分离出去，能够提取出跳频信号2。

图5 二次灰度形态学滤波后的时频图

图6 SNR=5 dB 时，基于MeanShift 的连通域标记图

图8 SNR=5 dB 时，跳频信号1 提取

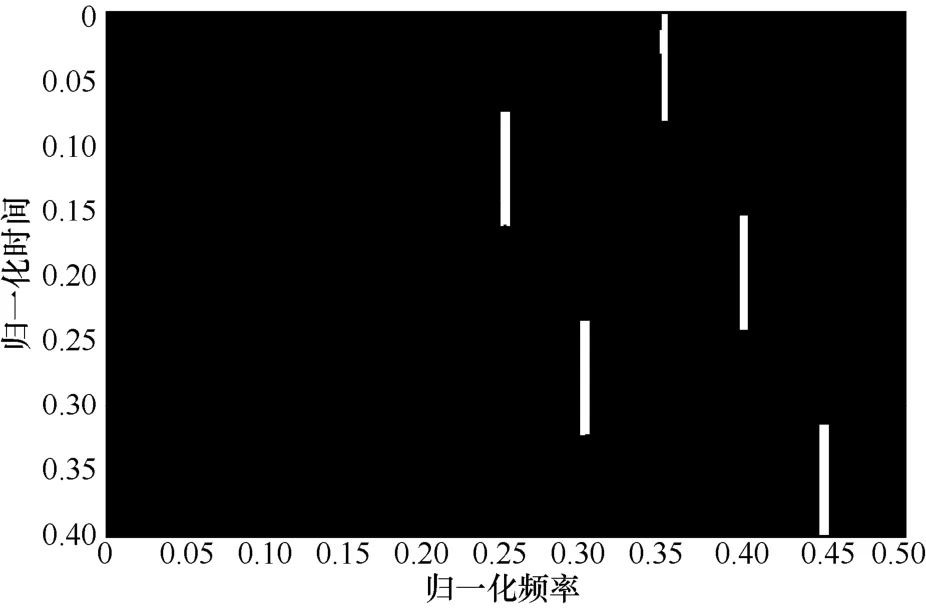
图9 SNR=5 dB 时，跳频信号2 提取

实验3算法抗干扰能力

为了进一步分析本文算法与文献[21,23]所述算法在不同SNR 下的抗干扰能力，SNR 设置为0～15 dB，由于在低SNR 下噪声能量较大，导致预处理后强噪声没有被完全滤除，误判为突发干扰信号，时频图上有跳频信号1、跳频信号2、突发干扰和定频干扰4 种信号，因此低SNR 下，K-Means 算法设置聚类种类k=4；随着SNR 升高，噪声能量不断降低，预处理后噪声被完全滤除，时频图上仅有跳频信号1、跳频信号2 和定频干扰3 种信号，因此SNR较大时，对K-Means 算法设置聚类种类k=3。

文献[23]采用改进的K-Means 算法对连通域特征进行聚类提取，当确定聚类种类k时，能够提高聚类的稳定性，然而在复杂的短波电磁环境下，无法提前确定聚类种类k，该算法的稳定性将会急剧降低。由图10 和图11 可知，当SNR=5 dB 时，部分强噪声和扫频干扰信号无法完全滤除，若设k=3，将会导致标号为8、11 和17 的突发干扰信号被分类到跳频信号1 的类集合中，产生误判现象，造成虚警概率急剧提升。由图12 和图13 可知，当SNR=10 dB 时，时频图中无突发干扰信号，仅存在跳频信号和定频干扰信号时，若设k=4，将会导致标号为1、2、5、7 的跳频信号1 被分类到突发干扰信号的类集合中，造成跳频信号的检测概率大大下降，无法提取出跳频信号的全部Hop。同理，文献[21]提出基于K-Means 聚类的阈值分割算法，设k=2，仅适用于存在噪声与跳频信号的环境。由图7 和图14 可知，本文所提算法在不同SNR 下均能实现自动聚类且聚类结果稳定，在复杂的短波信道环境下抗干扰能力较强。而文献[21]和文献[23]的算法相比于本文算法在复杂的短波信道环境下的抗干扰能力略差。

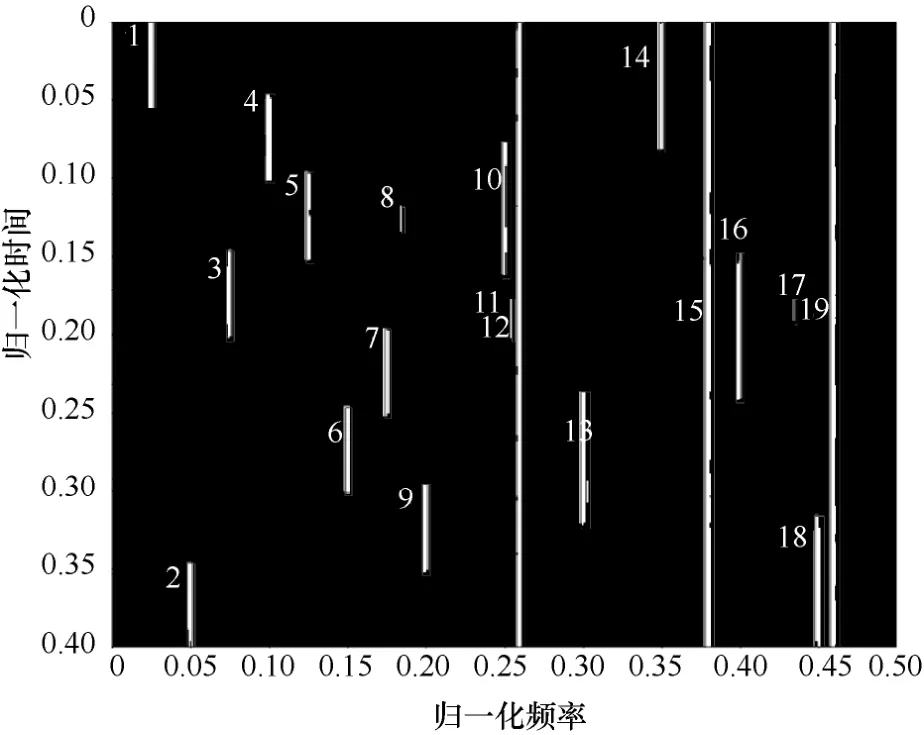
图10 SNR=5 dB,k=3 时，基于K-Means 的连通域标记图

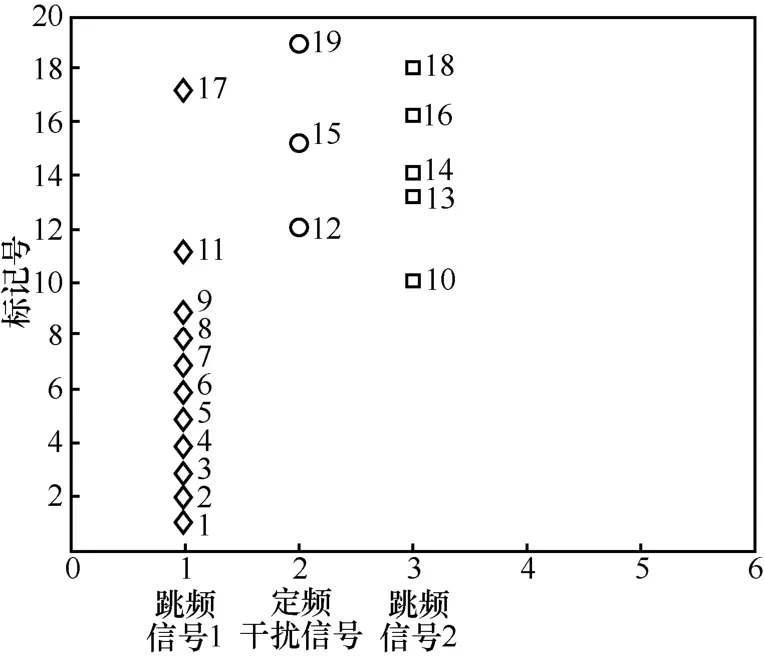
图11 SNR=5 dB,k=3 时，基于K-Means 的聚类结果

图12 SNR=10 dB,k=4 时，基于K-Means 的连通域标记图

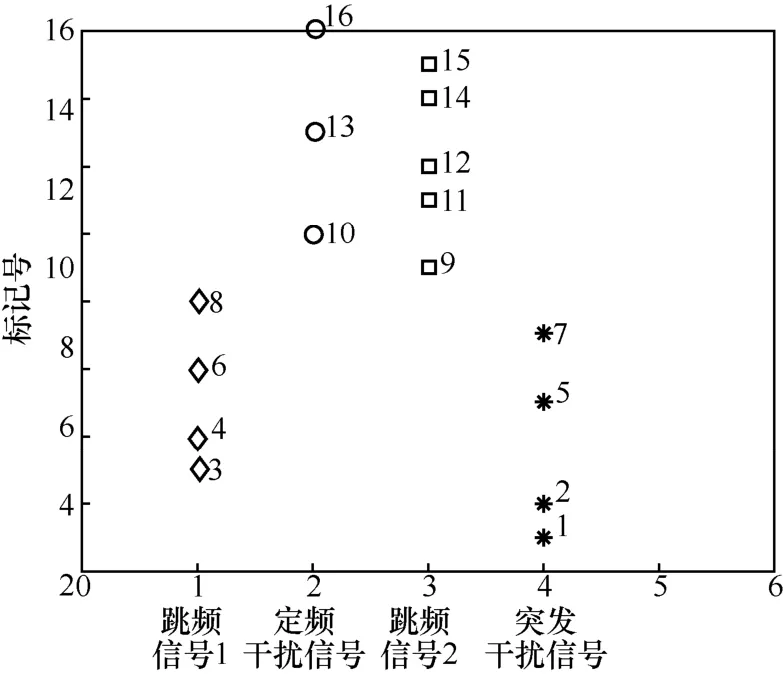
图13 SNR=10 dB,k=4 时，基于K-Means 的聚类结果

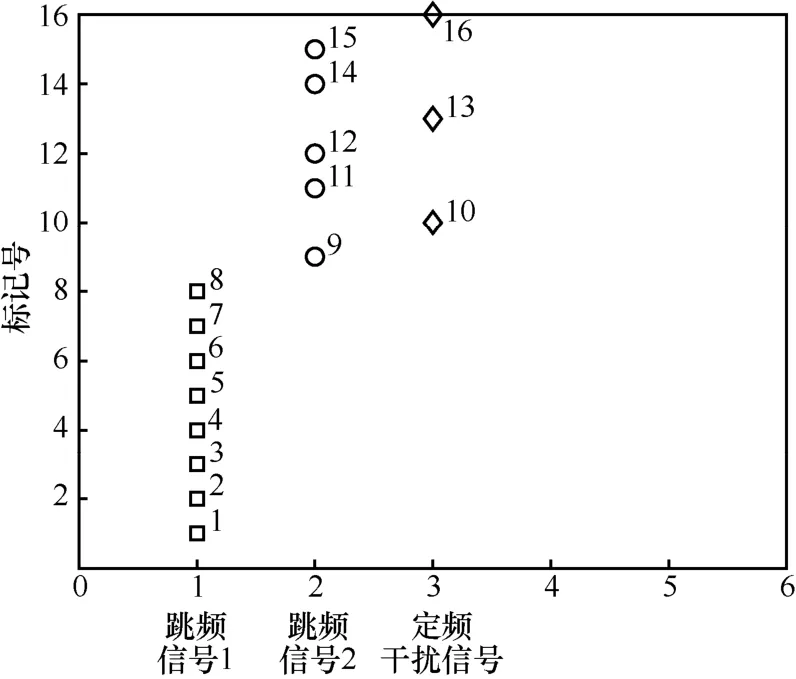
图14 SNR=10 dB 时，基于MeanShift 的聚类结果

实验4计算复杂度分析

对比本文所提算法与文献[21,23]算法的计算复杂度，如表1 所示。当SNR=5dB 时，针对时频分析、预处理、数据集个数以及聚类分析过程中需要进行处理的数据量进行分析。

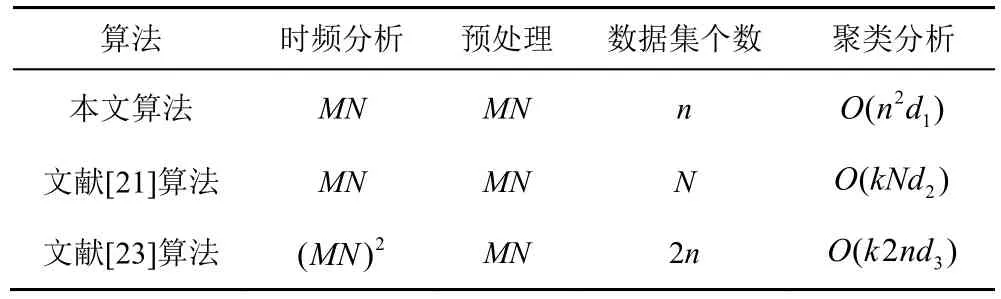
表1 算法计算复杂度对比

表1 中，M为时频矩阵的时间样点，N为时频矩阵的频率数，n为信号个数，k为K-Means 聚类种类，d1为本文算法的迭代次数，d2为文献[21]算法的迭代次数，d3为文献[23]算法的迭代次数。

由表1 可知，由于数据集个数N＞＞2n＞n，因此聚类迭代次数d2＞＞d3＞d1。文献[21]利用STFT 降低生成时频图的计算复杂度，但数据集个数较多，导致聚类分析过程中迭代次数增大，计算复杂度较大。文献[23]通过STFT 和WVD 联合分布生成时频图，进一步提高了低SNR 下跳频信号的检测概率，但极大地增加了时频运算复杂度。本文算法采用STFT 快速生成时频图，降低时频运算量，通过连通域标记计算信号的最大持续时长作为数据集，提取信号在时频图上显著特征的同时极大减少数据集的个数以及聚类分析的迭代次数，不仅降低了算法的计算复杂度而且提升了跳频信号的检测性能。

实验5检测性能

进一步分析本文所提算法在低SNR 下的检测性能，K-Means 聚类种类k设为4，进行1 000 次蒙特卡罗仿真实验。假设检测概率为Pd，虚警概率为fP，聚类提取后跳频信号的个数为a，当前SNR 下检测到跳频Hop 的个数为b，则检测概率Pd可描述为

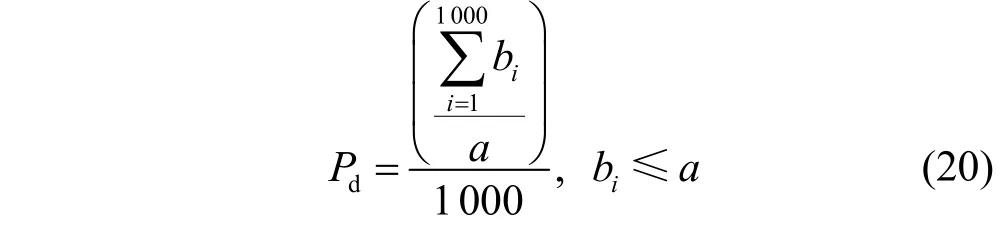
且虚警概率Pf可表示为[20,24]

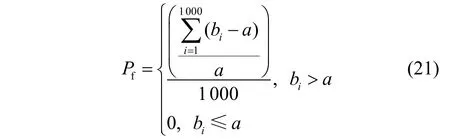
不同SNR下的检测概率和虚警概率分别如图15和图16 所示。由图15 可知，随SNR 增大，本文所提算法与文献[21]算法和文献[23]算法的检测概率均呈递增趋势；当SNR=5 dB 时本文所提算法的检测概率达到92%以上，在低信噪比下有较高的检测概率。由图16 可知，本文算法和对比算法的虚警概率均随SNR 增大而下降，其中本文所提算法的虚警概率最小，文献[23]算法次之，文献[21]算法的虚警概率最大。综上所述，随着SNR 降低，本文算法的检测性能增益逐渐增大，说明本文算法更适合于实现低信噪比下对跳频信号的盲检测。

图15 不同SNR 下的检测概率

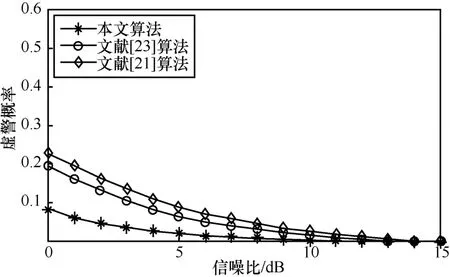
图16 不同SNR 下的虚警概率

4 结束语

在复杂的短波信道环境下，为了降低各种干扰信号和噪声对跳频信号的影响，实现低信噪比下跳频信号盲检测，本文提出了一种基于MeanShift算法的连通域标记跳频信号快速盲检测算法，以信号的最大持续时长为数据集进行聚类检测，分离各种干扰信号与噪声，提取跳频信号。仿真结果表明，在无任何先验信息的情况下，所提算法在低信噪比下有较高的检测概率和较低的虚警概率，对比其他跳频信号盲检测算法，不仅抗干扰能力较强，检测性能较好，计算复杂度也较低，聚类结果稳定。