逆断层作用下埋地连续钢管的力学性能

2022-07-10崔建阳钟紫蓝杜修力

北京工业大学学报 2022年7期

赵旭，崔建阳，钟紫蓝，杜修力

(北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124)

埋地钢管是目前石油、天然气等重要资源长距离输送最方便、最经济、最可靠的选择，其结构的安全性和可靠性一直受到人们的广泛关注.这些长距离埋地管道分布范围广，有时候不可避免地要穿越地震区域的活动断层，而地震引发的地层大变形，如断层运动、滑坡、场地液化等，是埋地钢管遭受震害的主要原因之一.震后灾害调查显示[1-2]，地震中断层的相对运动会对与之相交的管道产生严重的破坏，常见的破坏形态主要包括：管壁的局部屈曲、受拉失效、横截面过度变形，并导致巨大的经济损失和环境危害.因此，研究断层错动对埋地钢管受力与变形的影响具有重要意义.

国内外学者针对断层错动对管道的影响进了大量的研究.Ha等[3-4]和Abdoun等[5]通过双盒剪切箱对穿越走滑断层和正断层下的埋地高密度聚乙烯管道开展一系列试验研究，认为管道与断层的交角和管道的埋深对其轴向应变分布影响显著.Rojhani等[6]基于离心机试验研究逆断层作用下断层错动量、埋深和管径等关键因素对管道的轴向和弯曲应变的影响.Moradi等[7]通过3组离心机试验的研究结果表明管道的轴向应变远远大于弯曲应变，因此轴向应变是导致管道在正断层作用下破裂的主要原因.Jalali等[8]通过大型土箱试验研究逆断层错动对管道的影响，结果表明管道在逆断层作用下呈S形变形且有2处位置发生局部屈曲.Vazouras等[9]基于有限元方法讨论不同径厚比和内部压力下钢管穿越走滑断层的力学行为，并给出不同管道-断层交角下管道发生破坏的极限断层位移.Joshi等[10]采用梁单元模拟管道和离散非线性弹簧模拟管周土体，分析埋地管道在逆断层作用下的力学行为.Cheng等[11]基于数值模拟手段探讨了不同类型断层作用下管道的屈曲破坏，结果表明管道发生屈曲破坏的先后顺序依次为逆断层、走滑断层和正断层.张志超等[12-13]通过振动台试验输入位移时程模拟走滑断层运动，研究管道应变沿轴向的分布规律，并探讨管道与断层夹角和管内液体对管道周边土压力的影响.田江平等[14]通过土箱装置进行管道跨斜滑断层的模型试验，并以有限元软件加以模拟，给出管道的应变分布和变形特点.金浏等[15]对钢管和聚乙烯塑料管在逆冲断层作用下的整体屈曲及局部屈曲进行分析，讨论管径、壁厚、断层倾角、管道埋深等对管道屈曲模式的影响.曾希等[16]采用土箱试验装置模拟不同形式的断层错动，得到埋地管道的应变分布及整体变形特点，并与数值模拟结果进行对比验证.任翔等[17]分别在静力荷载和地震作用下，对不同类型断层位错下的连续管道进行有限元模拟分析及对比.

综上所述，虽然以往的研究对断层作用下的埋地管道的力学性能和变形特征进行了深入探讨，但仍存在一些不足：

1) 在埋地管道穿越逆断层的数值模拟中，大多数研究只是着重讨论管道的单一破坏模式及关键参数影响规律.但是实际情况下，断层作用下的埋地管道可能具有多种失效模式，具体哪种失效模式起控制作用尚未有深入讨论.

2) 不同失效模式与相应临界逆断层错动量之间关系的探讨相对有限.

本文以黏土中X65型埋地钢管为例，建立三维有限元数值模型，系统研究断层倾角、管道内压、管道径厚比对管道在逆断层作用下的力学行为影响，以期为实际工程中逆断层作用下的埋地钢管的设计和安全评价提供可靠的指导与建议.

1 埋地管道的力学性能评价标准

管道的主要作用是保证石油、天然气等重要资源的有效供应，而以往震害表明[1-2]，在断层运动的作用下埋地钢管的主要破坏形式包括以下3种：1) 跨断层埋地钢管产生的变形超出管道的极限抗拉承载力而导致管壁发生拉裂.2) 埋地钢管由于断层错动导致管壁过度压缩产生明显的管壁褶皱和屈曲，引起显著的局部压应变，进而导致管壁破坏.3) 当管道的截面发生严重的不规则变形后，会影响管道的正常运行效率和内部周期性安全检查，甚至可能导致管道输送功能的瘫痪.因此，管道的力学性能通常以基于应变或变形的极限状态来描述.基于上述讨论，本文主要对埋地钢管3种不同性能极限状态进行描述和量化，即管道的纵向极限拉伸应变、管道的局部屈曲、管道的横截面极限椭圆率.

1.1 纵向极限拉伸应变

管道纵向极限拉伸应变的确定对于建立基于应变的管道设计方法至关重要.在管道没有严重缺陷和损伤的情况下，抗拉能力主要受环焊缝强度的控制，通常该处会由于焊接缺陷和应力集中最先发生受拉断裂.加拿大标准油气管道系统设计标准CSA Z662[18]对埋地钢管环焊缝的极限拉应变提供了一种简单和直接的估算方法：

(1)

式中：εTu为临界拉伸应变；δc为焊缝裂纹尖端开口位移的韧性；λ为管道屈服强度与抗拉强度之比；ξ为管道缺陷长度与管壁厚度之比；η为缺陷高度与管壁厚度之比.式(1)中参数可按以下范围取值:0.1≤δc≤0.3，0.7≤λ≤0.9，1≤ξ≤10和η≤0.5.对于有轻微缺陷的管道，假定δc=0.1，λ=0.7，ξ=1，η=0.1，由此可以计算出εTu为1.5%.

考虑到式(1)中的预测比其他国际通用的基于应变的管道拉伸应变设计标准的建议值更为保守，比如：挪威船级社海底管线系统设计标准DNV-OS-F101、美国土木工程协会埋地钢管设计规范ASCE-ALA、印度理工学院坎普尔分校埋地管道抗震设计规范IRRK-GSDMA、欧洲标准化委员会欧洲法规8抗震设计第4部分Eurocode 8-part 4(见表1)，且X65钢管具有一定的延性，因此选择管道的εTu为2.0%.

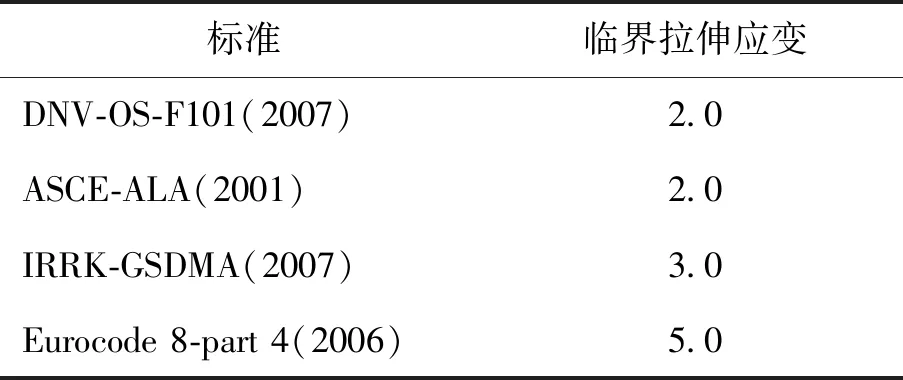
表1 管道临界拉伸应变的参考值[19-22]Table 1 Reference for limit value of pipeline tensile strain[19-22] %

1.2 局部屈曲

在断层运动作用下，管道壁也可能发生受压变形.当压缩应变超过一定限度时，管壁会因失稳出现局部屈曲或褶皱状态.通常，即使存在这些褶皱，但只要材料具有足够的延性，并且没有发生管壁局部破裂，管道仍然可以发挥其运输功能.因此，根据CSA Z662[18]规范给出的相关说明，局部屈曲的临界压缩应变可以表示为

(2)

(3)

式中：εCu为临界压缩应变；t为壁厚；D为管道直径；σh为环向应力；E为管道材料弹性模量；P为管道内部压力；σy为管道材料的屈服应力.

1.3 横截面极限椭圆率

管道横截面的过度变形是断层错动下管道的一种常见破坏模式，当管道所遭受的断层错动量较大时，管道的横截面会由圆形发展成为椭圆形，从而导致管道的抗弯刚度明显降低，影响管道内部的正常运行和检测维护.为了衡量截面的变形状态，一种简单而有效的方法是通过定义量纲一的参数——椭圆率f来量化管道变形的程度.

(4)

根据文献[23]的建议，当f的值变为0.15时，达到管道横截面压扁的极限状态，该值也被荷兰管线系统设计规范NEN 3650[24]所采纳.

2 三维数值分析模型

2.1 模型的建立

本文采用通用有限元分析软件ABAQUS建立X65钢管在逆断层运动下的三维数值分析模型，见图1.图1(a)中棱柱体的模型尺寸为60 m×10 m×5 m，采用八节点缩减积分实体单元C3D8R进行模拟，钢管的长度为60 m，直径为914.4 mm，采用四节点缩减积分实体单元S4R进行模拟.棱柱体的顶面为地表，按工程实践经验，钢管的埋深约为2倍的管径.为保证计算精度的同时提高计算效率，数值分析模型在靠近管道及断层面区域采用更为精细的网格划分，而在其余部分的网格相对比较稀疏，管道则在其与断层面相交附近20 m范围内采用精细化网格.图2为逆断层错动以后的土体-管道变形示意图，图中断层面与水平面之间的夹角为断层倾角β，是本文数值模拟研究中的关键参数.另外，目前有限元软件中模拟逆断层相对错动的2种方法为：1) 假设断层面为0厚度的接触面，土体模型以断层面为界分为2个部分，断层移动时一侧土体固定，另一侧土体发生断层错动.2) 包含断层的土体模型为一个整体的有限元模型，发生断层错动时两侧的土体不发生分离.由于第2种方法的土体变形主要集中发生在土体中部宽度为W的狭窄横向断层破裂区域内，无需建立上下盘之间的接触关系，也是近年来关于断层数值模拟研究的一种常见做法.本文借鉴Vazouras等[9,25]研究成果取断层宽度W=0.33 m.

图1 逆断层-管道三维数值分析模型Fig.1 Three-dimensional numerical analysis model of a pipeline crossing a reverse fault

图2 逆断层错动下土体-管道分析模型的变形示意图Fig.2 Deformation diagram of soil-pipeline analysis model under reverse fault dislocation

2.2 模型材料相关参数

Ramberg-Osgood模型可较好地模拟管道在达到极限抗拉强度之前的塑性变形，因此本文采用该模型作为X65管道的本构模型，应力应变关系式为

(5)

式中：ε为工程应变；σy为屈服应力；E为初始弹性模量；σ为应力；n和r为Ramberg-Osgood模型的参数.对于油气管道中的API 5L X65管道，σy=448.5 MPa，E=210 GPa，n=8，r=14[26-27].图3为X65管道的应力应变曲线.

土体本构模型采用Mohr-Coulomb理想弹塑性模型来描述其力学行为，由弹性模量E、泊松比μ、黏聚力c、摩擦角φ和膨胀角ψ表征，这些参数的值如表2所示.

表2 材料物理力学参数Table 2 Physical and mechanical parameters of materials

考虑到管道和土体材料的非线性性质以及各种材料接触界面处的粘结、滑移和分离等非线性行为，管道与土体间的相互作用采用接触面力学模型.管道外表面和土体间的接触设置可实现断层运动过程中的相对滑移(包括法向和切向位移)以及接触力的传递，从而更为真实地反映管道与土体之间的相互作用.其中界面的法向采用硬接触，即接触面之间能够传递的接触压力大小不受限制，当接触面的压力变为负值或者零就表示2个接触面发生分离.而界面的切向采用库伦摩擦定律，即当接触面之间的切向剪应力值超过所限定的临界值时，管道与土体之间将发生相对的滑移，其中摩擦因数取值为0.3[9,25].

2.3 模型的等效边界

断层发生错动时，埋地管道发生大变形的区域一般集中在断层附近的几米到十几米处，但实际上断层的运动会对上百米的管道产生影响，因此，为了提高计算效率，在ABAQUS有限元模型中，壳体管道的每一端通过线性轴向约束连接到轴向连接件单元CONN3D2，该单元用于模拟轴向等效边界非线性弹簧.从而反映壳体管道与超出其端部的其余部分的相互作用.本文采用刘爱文等[28]提出的等效边界法，当对管道有限元模型设置等效边界时，管道两端端部轴向上的外力荷载与非线性弹簧伸长量的关系式为

(6)

式中：F为施加在等效边界非线性弹簧的外力;ΔL为在外力作用下等效非线性弹簧的轴向伸长量；A为管道的横截面面积；E为管道材料的弹性模量；fs为沿管道轴向外表面单位长度的摩擦力.将管道和土体的基本参数值代入式(6)，可以得到管道等效边界非线性弹簧的位移量与轴力的对应关系.其中估算的fs=30.702 kN/m，与之屈服时相应的位移U0=0.004 5 m.

2.4 模型的数值模拟

数值分析的模拟过程分为3个步骤：1) 进行地应力的平衡.2) 对管道内表面施加内压.3) 对上盘施加相对应的位移，以模拟管道在逆断层中的运动.在步骤1)中，模型的上表面为自由面，模型的底面施加竖向约束，各个侧面施加其各自相对应的法向约束，对土体施加重力并进行地应力平衡.在步骤3)中，在施加逆断层位移前，应采用与实际工况相一致的边界条件，断层的两侧分别为上盘和下盘，其中下盘的底部及周围各侧面在各自对应的方向施加法向约束，以模拟断层错动时固定的下盘土体，而上盘则沿断层面同时施加轴向和垂向(即Z方向和Y方向)的位移，如图2所示，以用来模拟逆断层中上盘土体的运动.

3 有限元方法的对比验证

通过Jalali等[8]的埋地管道足尺试验数据和有限元软件数值模拟数据，验证了本文提出的有限元分析方法的有效性.表3列出管道足尺试验中管道和土体的相关特性参数.

表3 Jalali等[8]的埋地管道足尺试验参数Table 3 Full scale test parameters of buried pipeline by Jalali et al[8]

图3比较了基于本文有限元建模方法得到的数值计算结果与Jalali等[8]的试验及有限元结果.对比结果表明，本文采用的有限元建模方法可以有效反映逆断层作用下管道关键部位的应变分布情况，与试验和已有数值模拟结构吻合度较好.另外，从图3可以看出，有限元结果与试验结果的局部屈曲破坏位置略有差异，这可能是由于局部土体在断层错动下发生复杂变形(土体的流动、软化、裂缝形成等)以及管道试件本身有一点初始瑕疵(如焊缝不均匀性、焊接应力、初始变形等)造成的.而建立有限元模型时并没有考虑到这些实际因素的影响，导致有限元计算结果与试验结果存在差异.但总体来说，本文所采用的有限元方法适用于埋地钢管在逆断层作用下的失效模式分析.

图3 试验和有限元沿管道的应变分布Fig.3 Distribution of strain along the pipeline by test and finite element method

4 关键参数影响分析

4.1 不同断层倾角下管道的失效模式分析

按照断层倾角的不同构建D/t=96的无压三维管道-土体相互作用数值模型，研究不同断层倾角下断层错动对管道结构受力与变形的影响.

本节考虑了4种断层倾角：45°、60°、75°、85°.图4所示为断层错动量d=3 m时，不同断层倾角下管道的应力分布及局部屈曲模式.从图4可知，当断层倾角β=45°、60°、75°时，整个管道均出现2处局部屈曲的压溃模式，且这2处管段为应力集中区域；当断层倾角β=85°时，仅在上盘管道处出现局部屈曲.从管道的局部放大图可以看到上盘处管道的压溃形态较下盘区域更为严重.通过对比分析可知，断层下盘中局部屈曲的管段与断层面之间的距离随着断层倾角的增大而减小，而上盘中局部屈曲管段与断层面之间的距离随着断层倾角的增大基本不发生变化.

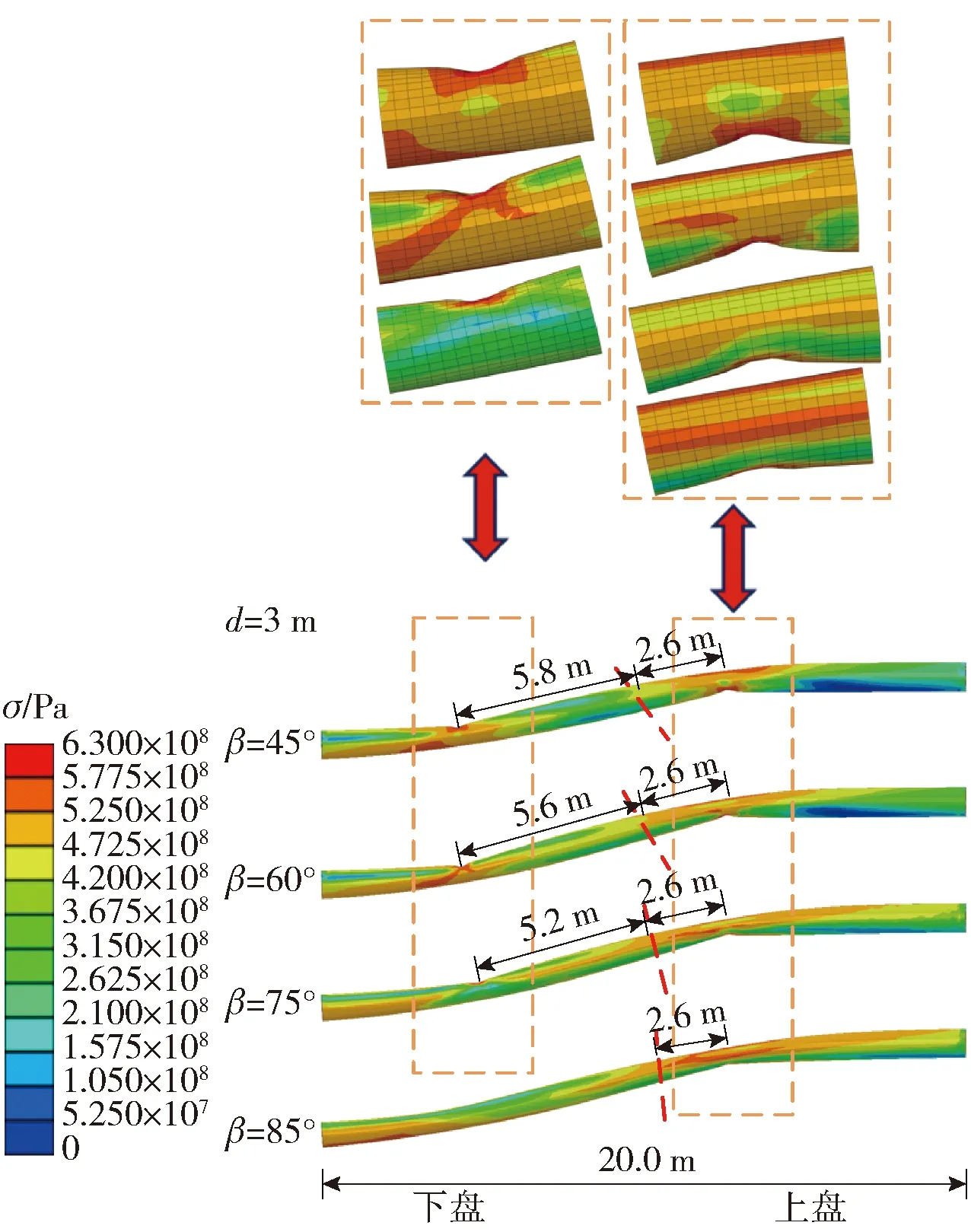
图4 不同断层倾角下管道的应力分布及局部屈曲模式Fig.4 Stress distribution and local buckling mode of pipeline under different fault dip angles

图5、6分别描述不同断层倾角下峰值应变和峰值椭圆率随着断层位移的变化(图例中T代表拉伸应变，C代表压缩应变).从图6可见，随着断层位移的增大，4种角度下管道均是先发生局部屈曲(管壁局部压缩应变超过临界压缩应变)，再发生管道的受拉失效(管壁拉伸应变超过纵向极限拉伸应变的2%).管道发生局部屈曲的断层倾角的先后顺序依次为75°、85°、60°和45°，这表明管道更容易在75°的倾角下发生局部屈曲的失效模式.从图6可见，管道发生横截面过度变形(f>0.15)的断层倾角的先后顺序与局部屈曲相一致.通过比较表4的临界断层位移可以发现，当β=45°、60°、75°、85°时，管道发生失效模式的顺序均依次为局部屈曲、横截面过度变形、管道的受拉失效.此外，对于管道的受拉失效、局部屈曲和横截面过度变形，临界断层位移随着断层倾角的增大呈现先减小后增大的趋势.这种现象可能是由于断层错动时竖向方向位移分量的变大，造成竖向方向的挤压作用明显，这时候管道更容易发生破坏，但是随着断层倾角的增大，断层错动下水平方向的位移分量相对较小，这时候管道轴向方向的压缩变形增长趋势放缓，从而导致管道整体破坏的减小.

图5 不同断层倾角下管道的峰值应变Fig.6 Peak strain of pipeline under different fault dip angles

图6 不同断层倾角下管道的峰值椭圆率Fig.6 Peak ovalization of pipeline under different fault dip angles

表4 不同断层倾角下管道失效所对应的临界断层位移Table 4 Critical fault displacement corresponding to pipeline failure under different fault dip angles

4.2 不同内压下管道的失效模式分析

考虑到管道是作为一种长距离输送液体或气体物资的运输工具，在运输过程当中，其内部的液体或气体势必对管道产生一定的环向压力.工程中对于管道能承受的工作压强极限计算公式为

(7)

式中Pmax为管道能够承受的最大工作压强.

按照管道内压的不同构建了β=60°，D/t=96的三维管道-土体相互作用数值模型，研究不同管道内压下断层错动对管道结构受力与变形的影响.

本节考虑了4种内压：0、10%Pmax、20%Pmax、40%Pmax.根据等式(2)(3)可知，内压P对管道的局部屈曲的εCu有一定的影响，具体表现为εCu随着P的增大而增大.

图7所示为断层错动量d=3 m时，不同内压下管道的应力分布及局部屈曲模式.从图中管道局部放大图可知，在不同内压下，管道呈现出不同的屈曲形态，具体表现为无压和低压下局部屈曲形态为压溃，而随着内压的增大，管道的局部屈曲模式由压溃转变为起皱，且内压越大，管道的起皱幅度越大.当P=0和P=10%Pmax时，整个管道均出现2处局部屈曲，但当P=20%Pmax和P=40%Pmax时，仅在上盘处管道发生皱起形态的局部屈曲.通过对比分析可知，上盘处管道的应力集中较下盘区域更为明显.上盘中局部屈曲的管段与断层面之间的距离随着内压变化较小，而下盘中局部屈曲管段与断层面之间的距离随着内压的增大而增大，直至局部屈曲管段消失.

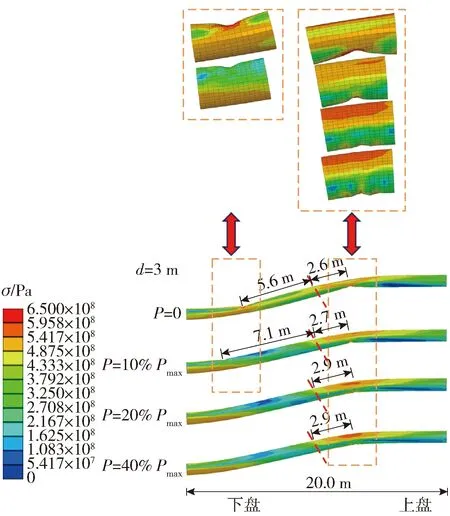
图7 不同内压下管道的应力分布及局部屈曲模式Fig.7 Stress distribution and local buckling mode of pipeline under different internal pressures

图8、9描述了不同内压下，峰值应变和峰值椭圆率随着断层位移的变化.从图8可见，4种不同的内压下，管道发生局部屈曲的先后顺序依次为0、10%Pmax、20%Pmax、40%Pmax，这表明当发生断层错动时，管道内压的增大会加强管道抗屈曲的能力.此外，从图8中可以看出，相对于无压状态，管道内压的增大加快了管道拉伸应变的发展，从而导致管道的受拉失效.从图9可见，随着断层位移的增加，直至断层位移达到3 m，管道的横截面变形仅在0和10%Pmax下达到f=0.15，这表明管道内压对横截面的变形有着一定的抑制作用.

图8 不同内压下管道的峰值应变Fig.8 Peak strain of pipeline under different internal pressures

图9 不同内压下管道的峰值椭圆率Fig.9 Peak ovalization of pipeline under different internal pressures

根据表5中不同内压下管道失效所对应的临界断层位移，可以得到当P分别为0和10%Pmax时，管道发生失效的顺序依次为局部屈曲、横截面过度变形、管道的受拉失效.当P=20%Pmax时，管道发生失效的顺序次为局部屈曲、管道的受拉失效.而当P=40%Pmax时，管道最先发生的失效模式为管道的受拉失效.此外，对于管道的受拉失效，临界断层位移随着管道内压的增大呈现不断减小的趋势；对于管道的局部屈曲，临界断层位移随着管道内压的增大呈现不断增大的趋势.

表5 不同内压下管道失效所对应的临界断层位移Table 5 Critical fault displacement corresponding to pipeline failure under different internal pressures

4.3 不同径厚比下管道的失效模式分析

按照管道径厚比的不同构建了β=60°下无压三维管道-土体相互作用数值模型，研究不同管道径厚比下断层错动对管道结构受力与变形的影响.

本节考虑4种径厚比：144.0、96.0、72.0和57.6.根据等式(2)(3)可知，D/t对管道的局部屈曲的εCu有着一定的影响，具体表现为εCu随着D/t的增大而减小.

图10所示为断层错动量d=3 m时，不同径厚比下管道的应力分布及局部屈曲模式.从图10可以看出，在相同内压状态下，管道的径厚比越大，管壁上的应力也越集中，局部屈曲的压溃破坏也越严重.随着管道径厚比的减小，管道的两处局部屈曲形态逐渐演化为应力集中区域，且断层下盘中局部屈曲管段和应力集中区域随着径厚比的减小逐渐远离断层面，而断层上盘中局部屈曲管段和应力集中区域随着径厚比的减小不发生变化.

图10 不同径厚比下管道的应力分布及局部屈曲模式Fig.10 Stress distribution and local buckling mode of pipeline under different diameter thickness ratios

图11、12描述了不同径厚比下，峰值应变和峰值椭圆率随着断层位移的变化.从图11可见，随着管道径厚比的减小，管道的局部屈曲和受拉失效的临界断层位移也随之减小.从图12可见，管道发生横截面过度变形的径厚比的先后顺序与局部屈曲、受拉失效相一致.

图11 不同径厚比下管道的峰值应变Fig.11 Peak strain of pipeline under different diameter thickness ratios

图12 不同径厚比下管道的峰值椭圆率Fig.12 Peak ovalization of pipeline under different diameter thickness ratios

通过比较表6中不同径厚比下管道失效所对应的临界断层位移可知，对于D/t分别为144.0、96.0，管道的主要失效模式为局部屈曲；对于D/t=72.0，管道的主要失效模式为横截面过度变形；而对于D/t=57.6，即使断层位移达到3 m，管道也尚未发生上述任意一种失效模式.这表明逆断层作用下的薄壁管道更容易发生破坏，增加壁厚可显著提高管道的抗变形能力.