基于双应力加速寿命试验的滚珠丝杠副可靠性分析

王 民，王树华，孙铁伟，石 龙

(1.北京工业大学机械工程与应用电子技术学院，先进制造技术北京市重点实验室，北京 100124；2.电火花加工技术北京市重点实验室，北京 100191)

现代制造业水平的飞速提升导致了人们对数控机床整体性能的要求越来越高，滚珠丝杠副是数控机床的重要传动部件，与数控机床整体的可靠性紧密关联，在数控机床、自动化装备、车辆交通及航空航天等领域常常用到[1].因此，对滚珠丝杠副的可靠性分析工作得到越来越多的科研机构和研究人员的重视.

近年来，随着可靠性工程的不断发展，相关的数据样本量较小.对于滚珠丝杠副产品，由于价格昂贵、可靠性水平较高，而且试验周期长，很难进行大样本的统计试验，甚至有的专项计划只生产1至2台产品.综合考虑上述情况，本文通过引入小子样、加速寿命试验的方法完成对单样本滚珠丝杠副的寿命评估.

在实际工况下，数控机床进给系统的滚珠丝杠在加减速运行过程中，润滑会变差，加剧接触部件的磨损，降低其精度和寿命[2]，进而导致数控机床的可靠性水平下降、加工质量变差.另外，根据Archard[3]磨损理论知道外界负载应力是影响磨损量的主要因素之一.因此本文将综合考虑转速和负载双应力对滚珠丝杠副可靠性寿命的影响进行加速寿命试验，然后通过对试验数据进行统计分析得到在加速应力条件下的寿命分布模型，最后利用加速方程外推出在正常应力水平下的寿命特征，完成对滚珠丝杠副的寿命评估[4-5].

为了提高小子样单样本滚珠丝杠副的可靠性评估精度，本文使用虚拟增广法对加速寿命试验得到的故障数据进行等价扩充，根据虚拟增广法扩充得到的数组和原试验数据的分布形式相同.然后对增广后的数组进行统计分析，从而达到提高试验评估精度的目的.

常用的可靠性寿命及故障分布模型有正态分布、指数分布、威布尔(Weibull)分布[6].其中Weibull分布是一类广泛应用于机械、电子、航天航空等领域的寿命分布模型，是目前较为常用的寿命模型之一.Weibull分布有多种参数估计方法[7]：其中图估计法易受人为因素影响，精度偏低；极大似然估计法求解烦琐，常常需要借助计算机；线性无偏估计法不适用于小子样情况，在大样本条件下还需借助查阅专用表格，虽然步骤简单，但表格量大且在无表格处无法使用此方法；最小二乘法求解简便，具有唯一最优解和好的解析性质，是Weibull分布参数估计的一种常用方法.

综合以上特点，本文针对小子样单样本滚珠丝杠副提出一种双应力三水平的加速寿命试验设计和统计分析方法，利用虚拟增广法和最小二乘法完成在3个步进加速双应力水平下的参数估计和可靠性评估，然后联立求解出加速方程，进而计算出滚珠丝杠副在正常应力条件下的寿命指标，完成对单样本滚珠丝杠副的可靠度寿命分析.

1 加速寿命试验模型

1.1 基本假定

滚珠丝杠副具有加速性的3个条件为：失效分布同一性、失效机理一致性和失效过程规律性[8].根据以上具有加速性的3个条件，本文提出3个基本假定.

假定1：样本在任意应力下的寿命T均服从Weibull分布，即T～W(m,η)，累积分布函数为

(1)

式中：η>0为尺度参数，表示特征寿命；m>0为形状参数.

假定2：样本在任意应力下的失效机理不变，由于Weibull分布中的形状参数反映失效机理，因此有

m1=m2=…≡m

(2)

假定3：样本特征寿命与试验双应力之间的关系模型选用Nelson广义对数线性模型，其数学表达式为

lnη=β0+β1φ1(V)+β2φ2(P)

(3)

式中：η为特征寿命；φ1、φ2常为应力的已知函数；β0、β1、β2为待估参数；V、P分别为转速和负载.

考虑到本文的2个应力均为非热应力，而且每个应力的加速效果均呈逆幂律形式，因此应力Vi、Pi与相对应的特征寿命ηi可以通过式(3)转化为双应力加速的逆幂律模型[9]：

(4)

对式(4)两边取对数，得到加速方程的对数形式为

lnηi=lnA-αlnVi-βlnPi

(5)

式中A、α、β均为常数.

1.2 加速系数

加速系数是指滚珠丝杠副在正常应力组合(V0,P0)与加速应力组合(Vi,Pi)下达到特征寿命需要时间T0和Ti的比值，记为τ.即

(6)

由式(4)(6)可得加速系数理论公式为

(7)

1.3 可靠性指标

滚珠丝杠副是可修复、可更换系统，出现故障后，可对零部件进行修复或更换，并且记录故障时间和修复时间，然后继续进行试验.

将平均故障间隔时间作为可靠性定量指标.其表达式为

(8)

式中Γ为伽马函数，其值可以通过查阅伽马函数标准表[10]得到.

在特定工作条件下，将滚珠丝杠副零部件出现故障的概率称为寿命可靠性.由假定1可知滚珠丝杠副可靠度的数学表达式为

(9)

2 加速寿命试验

2.1 加速寿命试验方案设计

试验选用国产双螺母预紧式滚珠丝杠副为研究对象，其结构参数见表1[11].本文综合考虑转速以及轴向负载作为加速寿命试验的2个应力，分别将其记为V和P.额定转速V0和额定负载P0分别为500 r/min、1 000 N.如果每个应力选定3个加速水平，则共有3×3=9个应力组合，如果将这9个应力组合全部进行试验，则会大大延长试验周期，降低试验效率.因此按照低、中、高3个水平对加速应力进行合理等级划分，根据对角线原则分别选取(V1,P1)、(V2,P2)、(V3,P3)作为3个步进加速双应力进行定时截尾试验.由于试验过程中滚珠丝杠副的失效机理不能改变，综合考虑试验方案和加载能力，结合工程经验，本文选取轴向负载大小分别为5%Ca、10%Ca、15%Ca(Ca为额定动载荷)，具体载荷大小如表2所示.

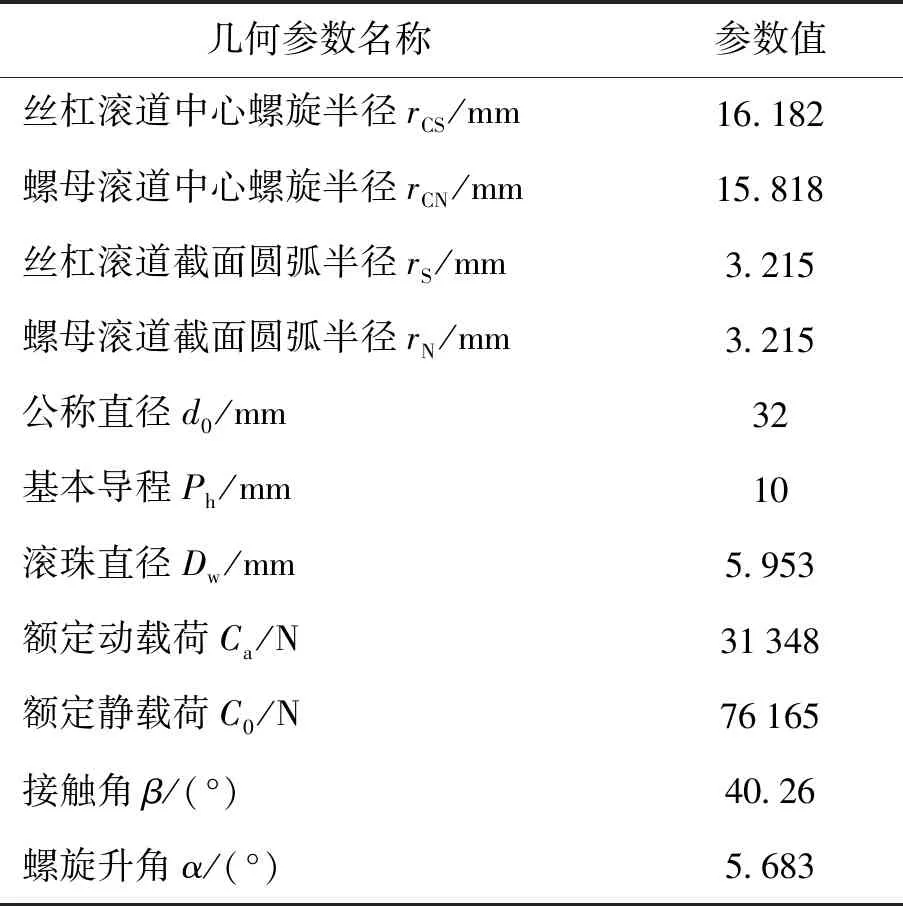
表1 滚珠丝杠副的参数Table 1 Parameters of the ball screw

表2 加速试验应力组合方案Table 2 Stress combination scheme of accelerated test

考虑到试验对象为小子样单样本滚珠丝杠副，为了满足虚拟增广法的适用要求，提高其可靠度寿命的评估精度，提出在不同步进加速应力组合下的试验截尾时间设定准则：在每个步进加速双应力组合下出现至少2～3个非关联性故障，并将最后一个故障时间记为该步进加速双应力组合下的试验截尾时间，即当在第1个步进加速双应力下发生至少2～3个非关联性故障时，提升应力，继续在第2个步进加速双应力水平下进行试验，以此类推，直至试验结束.

整个试验过程中环境温度保持在(20±5) ℃，湿度最大为90%，要定期进行润滑，润滑条件包括润滑剂种类、润滑间隔时间、润滑量等必须按照具体说明书执行.首先对丝杠进行加载跑合，排除由于设计等问题引起的早期故障，确保在各个加速应力载荷阶段无异常，然后在滚珠丝杠副可靠性试验仪器上进行模拟加载，对其进行较为全面的试验，在试验过程中对摩擦力矩、噪声、振动、温升等性能参数进行实时监测和记录，如果滚珠丝杠副出现超过允许值的噪声和振动，则判定为故障，修复或更换受损部件后继续进行试验并记录时间作为一次寿命点.如果经过修复后仍无法正常工作即发生不可修复故障，则视为失效，停止试验.

对可靠性进行评估时，关键的步骤之一是弄清故障的判定和分析方法，这直接影响到评估结果的准确性.对于滚珠丝杠副来说，故障是指产品在规定的工作运行条件下，一个或某几个功能丧失，或是性能参数超过允许界限，也包括滚珠丝杠副螺母、滚珠、回珠器等元部件的破损和断裂.具体故障判据如下[12]：

1) 滚珠丝杠副的任一零部件发生松动、损伤、破裂或局部断裂；

2) 检测系统采集到的摩擦力矩、振动、噪声等数值在某一段监测时间间隔内偏离正常范围；

3) 丝杠传动不平稳，无法正常运行.

根据以上判据对可靠性试验过程中滚珠丝杠副出现的故障进行统计分析，并将其按照文献[13]中表5.2滚珠丝杠副的关联故障和非关联故障完成分类.

2.2 加速寿命试验统计分析

本文在定时截尾双应力加速寿命试验的基础上，利用虚拟增广法对试验数据进行等价扩充以满足参数估计方法的要求，提高在单样本情况下的寿命评估精度.虚拟增广法的立论依据：增广后子样均值应与原来的子样均值相等；增广后的子样标准差应与类似件的子样标准差相等[14].为使虚拟增广得到的故障时间数据样本更为合理，使用近似公式

(10)

对试验得到的故障数据进行增广至m.式中：T0为样本均值；c为待定系数；σ为样本标准差；T为增广后的样本值.

利用近似公式(10)将试验样本数据增广至m=10个，那么增广后的样本数据T1～T10可以表示为

(11)

根据虚拟增广法的2个立论依据可以列出方程：

(12)

(13)

根据式(12)(13)可求解得c=0.135 0，综合试验数据及式(12)可以求出增广后的样本数据分别为

(T0-1.831 0σ)，(T0-1.089 0σ)，
(T0-0.559 0σ)，(T0-0.241 0σ)，
(T0-0.135 0σ)，(T0+0.135 0σ)，
(T0+0.241 0σ)，(T0+0.559 0σ)，
(T0+1.089 0σ)，(T0+1.831 0σ)

然后，将虚拟增广后的数据利用最小二乘法进行统计分析，具体做法如下.

将累积故障分布函数做如下线性变换：

(14)

其中，令

(15)

则式(14)可转换为Weibull分布线性模型

y=bx+a

(16)

在每个步进加速双应力情况下，通过试验得到的故障时间对应的累积故障概率采用近似中位秩公式表示，其经验分布函数为

(17)

式中n为样本数据总数.那么对于一组增广后的试验数据

(ti,Fn(ti)),i=1,2,…,n

(18)

根据式(15)可转换为

(19)

将线性模型y=bx+a通过最小二乘法进行拟合，可以求出待估参数b、a的表达式分别为

(20)

(21)

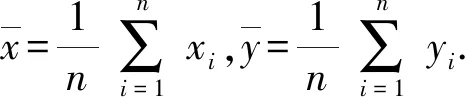
综上，求出Weibull分布中两参数的点估计为

(22)

求出模型参数后进行模型验证，判定故障间隔时间是否符合Weibull分布模型，常用的验证方法有拟合优度检验和假设检验.

1) 拟合优度检验

可用相关系数r表明数据xi、yi的拟合情况，其表达式为

(23)

相关系数越趋近于1，说明寿命分布服从Weibull模型越好.显著性水平为α时通过查表确定相关系数起码值rα.当r>rα时，认为回归效果显著；反之，认为回归不显著.可以据此来判定故障数据服从Weibull分布的好坏情况.

2) 假设检验

基本思想：先提出两个对立的假设，根据试验数据计算出检验统计量，然后根据检验统计量决定其中某一个假设成立，完成检验.常用的模型检验方法有卡方检验和柯尔莫戈洛夫(Kolmogorov-Smirnov,KS)检验[15].其中，卡方检验对小样本的检验精度不如柯尔莫戈洛夫检验，因此选用KS检验法对试验模型进行假设检验.

KS检验法将经验分布函数Fn(t)和统计分析得到的模型累积分布函数F0(t)进行对比，原假设H0与备择假设H1如下.

H0：故障间隔时间服从Weibull分布

H1：故障间隔时间不服从Weibull分布

其检验统计量

Dn=sup|F0(ti)-Fn(ti)|=max{di}

(24)

通过查KS检验临界值表可以得到在显著性水平为α时Dnα的值.如果有Dn≤Dnα，则H0成立，故障间隔时间数据服从Weibull分布；反之，H1成立，Weibull寿命分布模型不适用.

3 加速寿命试验仿真算例

对样本进行加速寿命仿真试验，其结构参数如表1所示，所施加的载荷应力如表2所示.然后借助数学方法和计算机得到需要的模拟故障数据，其具体步骤如下.

对Weibull累积分布函数式(1)进行逆变换得到其反函数为

(25)

其中随机变量y服从均匀分布U(0,1)，y与1-y为同分布，所以可转换为

(26)

可以通过计算机MATLAB软件产生基于均匀分布U(0,1)的随机数y，然后计算出F-1(y)的值.

结合上述方法以及截尾时间设定准则，根据文献[16]中的滚珠丝杠副的形状参数m=1.65，特征寿命η分别取800、480、350 h得到在3个步进加速双应力水平下的模拟故障间隔时间数据并按从小到大排列，如表3所示.

表3 加速应力下的模拟数据Table 3 Simulation data under accelerated stress

对加速应力下的故障间隔时间数据进行分析，根据式(11)(12)(13)得到每一个步进加速双应力下的虚拟增广后的数据如表4所示.

表4 经过虚拟增广后的数据Table 4 Data after virtual augmentation

依据最小二乘法原理，通过MATLAB软件分别对3个步进加速双应力下增广后的数据进行直线拟合，拟合结果如图1所示.

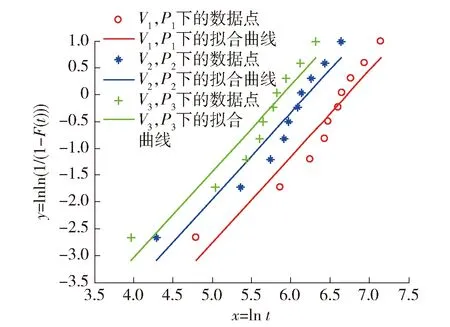
图1 数据拟合曲线Fig.1 Data fitting curve

从图1可以看出，在3个步进加速双应力水平下拟合得到的直线基本保持平行，斜率近似相等，即形状参数保持不变，从而验证了假定2的正确性，即在不同的加速应力组合下，样本的失效机理没有发生改变.

由表5分析可知，3条拟合直线的相关系数都很接近于1，说明线性相关度很高，拟合效果较好.

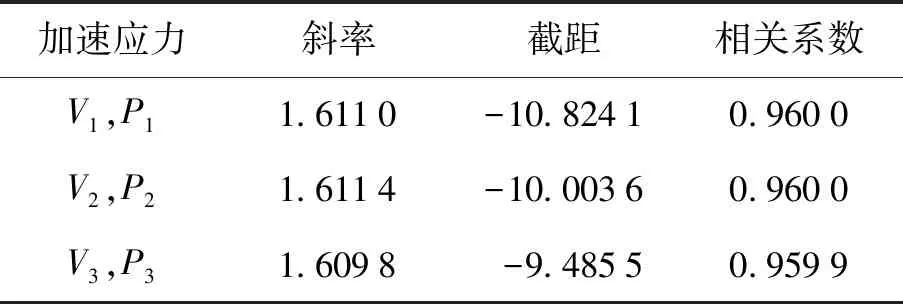
表5 拟合直线数据Table 5 Data of the fitting line

结合式(22)可求得在3个步进加速双应力下的形状参数分别为

m1=1.611 0,m2=1.611 4,m3=1.609 8

为满足假定2，形状参数取各加速应力组合下所求得的形状参数的平均值，即

将m的值代入式(22)中的第2个式子，进而求出在3个步进加速双应力下的特征寿命分别为

η1=828.92,η2=498.06,η3=361.06

再将以上特征寿命数据代入式(5)，联立求解可得

A=6.145 3×105,α=0.469 2,β=0.460 4

因此加速方程为

lnηi=13.328 6-0.469 2lnVi-0.460 4lnPi

(27)

将(V0,P0)代入式(27)求出正常应力条件下的寿命为η0=1 383.0 h.

根据式(9)可知滚珠丝杠副在额定载荷下的可靠度函数为

由式(8)可知滚珠丝杠副的MTBF为

4 应用讨论

滚珠丝杠副在实际使用中，一般可分为高速轻载、低速重载等情况，以下结合加速方程对不同工况下的寿命可靠度进行分析讨论.

由加速方程式(27)可以求出在高速轻载(V3,P0)和低速重载(V0,P3)工况下的特征寿命分别为

η30=721.68,η03=691.93

根据式(9)可知在这两种工况下的可靠度函数分别为

不同工况下的可靠度函数图形如图2所示.

图2 滚珠丝杠副不同工况下的可靠度函数Fig.2 Reliability function diagram of ball screw under different working conditions

从图2中可以看出，在相同可靠度的情况下，滚珠丝杠副在高速轻载下的寿命比在低速重载下的寿命略大，均远小于在额定载荷下的可靠度寿命，与实际相符.

5 结论

1) 为了在滚珠丝杠副可靠性寿命试验中综合考虑速度和负载两个应力水平对可靠性寿命的影响，本文提出一种双应力三水平的加速寿命试验设计和可靠性分析方法，通过建立双应力加速寿命试验模型并采用最小二乘法对故障数据进行统计分析，建立滚珠丝杠副的加速寿命试验的双应力加速方程.为进一步开展滚珠丝杠副实际不同工况条件下寿命评估提供方法和依据.

2) 本文提出利用虚拟增广法对小子样单样本条件下双应力寿命试验数据进行等价扩充后得到不同应力水平下的威布尔分布参数，并建立加速寿命试验的加速方程的方法.该方法可以满足小子样单样本试验条件下滚珠丝杆副可靠性寿命评估的精确性要求.并且，本文给出了仿真算例验证了所提出方法的有效性.