电磁超材料中微波吸波体结构参数对电磁谐振的影响研究

摘  要：为了提高电磁超材料的性能，研究电磁超材料中微波吸波体结构参数对电磁谐振的影响。选择CST Studio Suite 2021版仿真软件，构建微波吸波体结构模型;依据阻抗匹配理论通过D.R.Smith提取法提取微波吸波体本构参数，生成无源Maxwell方程和电磁波传播Helmholtz方程;计算微波吸波体结构的相对等效电磁参数，确定电磁超材料中微波吸波体结构参数对电磁谐振的影响。实验结果表明：微波吸波体结构参数可以改变电磁谐波的波动频率、波动和吸收率，与该文研究成果一致。

关键词：电磁超材料;微波吸波体;结构参数;电磁谐振;影响研究

中图分类号：TP391.9        文献标识码：A文章编号：2096-4706（2022）05-0053-04

Research on Influence of Structural Parameters of Microwave Absorber in Electromagnetic Metamaterials on Electromagnetic Resonance

XI Bailin

（The 10th Research Institute of China Electronics Technology Group Corporation， Chengdu  610036， China）

Abstract： In order to improve the performance of electromagnetic metamaterials， the influence of structural parameters of microwave absorbers in electromagnetic metamaterials on electromagnetic resonance is studied. The structural model of microwave absorber is constructed by selecting CST Studio Suite 2021 simulation software; according to the impedance matching theory， the constitutive parameters of microwave absorber are extracted by D.R. Smith extraction method， and the passive Maxwell equation and electromagnetic wave propagation Helmholtz equation are generated; the relative equivalent electromagnetic parameters of microwave absorber structure are calculated， and the influence of microwave absorber structure parameters in electromagnetic metamaterials on electromagnetic resonance is determined. The experimental results show that the structural parameters of microwave absorber can change the fluctuation frequency， fluctuation and absorptivity of electromagnetic harmonics， which is consistent with the research results in this paper.

Keywords： electromagnetic metamaterial; microwave absorber; structural parameter; electromagnetic resonance; influence study

0  引  言

超材料属于一种新型材料，具有其他材料所不具有的超常物理性质，且在实际应用中，还可以根据超材料的关键物理尺度设计材料结构。基于此，在电子产品时代，人们非常重视电磁超材料的研究，降低众多电子产品产生的电磁干扰。

1  电磁超材料中微波吸波体结构参数对电磁谐振的影响研究

1.1  设计电磁超材料中微波吸波体结构模型

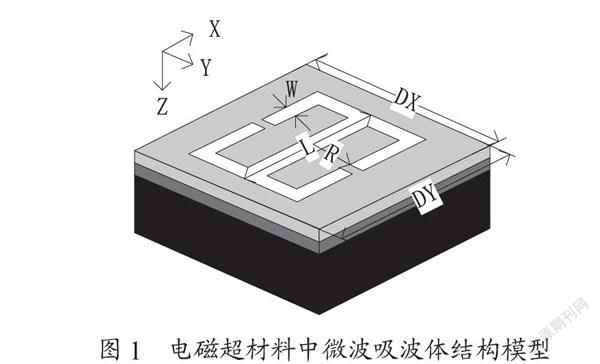
将电磁超材料中微波吸波体结构模型仿真环境的背景材料设置为Normal，在这一背景条件下，依据右手坐标系原则，构建电磁超材料单元胞[1，2]，并进行以下设定：（1）将单元胞中的周期结构单元记为z轴，属于电磁超材料中微波吸波体结构中的入射方向;（2）Normal背景的长度为6.9 mm;（3）单元胞中的周期结构单元位于Normal背景的中央位置;（4）电边界记为y轴;（5）磁边界记为x轴;（6）周期结构单元属于二维无限延伸结构;（7）z轴方向存在电磁入射端口和出射端口;（8）电磁波可以直接射入周期结构单元。根据上述八条设定内容，最终得到了如图1所示的模型。

图1  电磁超材料中微波吸波体结构模型

图1中，（X，Y，Z）表示电磁超材料中微波吸波体结构模型在三维空间中所处坐标方向;D表示单元周期长度;W表示臂宽;R表示半径;L表示臂長。此次研究设计的电磁超材料中的微波吸波体结构模型主要包括硅基底、谐振、氟化镁膜、金属膜四层结构，其中硅基底位于最底层，材料本身的折射率为3.44;硅基底上一层为连续金属膜，主要金属材料为金;金属膜上一层为连续氟化镁膜;最上层为类似于“冚”字结构的谐振层，主要原料为金属。

1.2  提取微波吸波体结构模型参数

由于不同结构参数的微波吸波体所产生的本构参数不同，且很难通过显微镜等微观手段确定微波吸波体的折射率、阻抗、S参数等本构参数[3，4]。为此，将微波吸波体平板介质分为均匀和不均匀两种，并依据阻抗匹配理论通过D.R.Smith提取法提取微波吸波体本构参数。

当微波吸波体的平板介质属于均匀平板介质时，其电磁波从介质板的一面传输到另外一面，则可以根据D.R.Smith提取法生成如（1）式所示的矩阵：

（1）

其中，C表示电磁波传播矩阵;S表示硅基底;SZ表示S的折射率;b表示S在自由空间中的波数;Sh表示S的厚度;r表示S的波阻抗;E表示电磁场强度;ER表示右边E;EL表示左边E。

在（1）式所示的电磁波传播矩阵基础上，根据接地测量出的散射场强度和相位，进行求逆运算，最终得到超材料的等效介电常数和磁导率表达式，如式（2）所示：

（2）

其中，j表示超材料的等效介电常数;c表示超材料的磁导率。

当微波吸波体的平板介质属于不均匀平板介质时，其入射波的反射过程会受材料本身阻抗的干扰，产生电损耗和磁损耗[5，6]。为此依据阻抗匹配理论提取不均匀平板介质损耗特性，此时，生成的吸波器内的无源Maxwell方程和电磁波传播Helmholtz方程如式（3）所示：

（3）

其中，e表示电磁波;▽表示梯度算子;i表示单位虚数;α表示电磁波入射角频率;αŋ表示吸波体介质磁导率;δ表示复磁场的振幅;χ表示阻尼频率。

由式（3）可知，j值和ŋ值越大，吸波体介质在运行过程中，其吸收电磁波时所产生的损耗就会随之增加。因此，不同结构参数的微波吸波体具有不同的介电常数、磁导率;当介电常数、磁导率过高时，则会增加微波吸波体阻抗，降低微波吸波体与空气阻抗特性的匹配度，增加微波吸波体吸收电磁能量损耗;反之，当介电常数、磁导率值过低时，则会降低微波吸波体阻抗，提高微波吸波体与空气阻抗特性的匹配度，减少微波吸波体吸收电磁能量损耗。

1.3  确定微波吸波体结构参数对电磁谐振的影响

根据此次研究建立的微波吸波体结构模型，以及提取到的模型参数，采用反演法确定微波吸波体结构参数对电磁谐振的影响，下面介绍其计算过程。

假设电磁波入射微波吸波体时，不同结构参数微波吸波体的反射系数和透射系数相同，则可以根据式（1）、式（2）和式（3），确定电磁波能量e'在材料中是有衰减的，即e'≥0，实际材料的阻抗r必须为正值，即r≥0。

若电磁波从Z轴方向射入，则微波吸波体最上层的金属膜会在X-Y平面上无限次重复性地吸收电磁波，按照从最上层到基层的传播规律依次传播，此时，电磁波就会受到不同微波吸波体结构参数产生的不同反射系数和透射系数影响，改变电磁波参数（即微波吸波体结构的相对等效电磁参数），其表达式如式（4）所示：

（4）

其中，μ表示等效磁导率;V表示金属开口环与整个结构的体积比;b表示单元周期;z1表示微波吸波体最上层金属膜表面电阻;c0表示真空磁导率;v表示真空中光速[7]。

根据式（4）计算得到的等效电磁参数，可以确定电流在微波吸波体上的分布情况，其表达式如式（5）所示：

其中，I表示微波吸波体上电流分布函数;m表示电流密度。

根据式（4）和式（5）计算得到的等效电磁值和电流值，在此次研究选择的CST Studio Suite 2021版电磁仿真软件中[8]，将微波吸波体最上层的金属膜结构分别设置为以下数值：样本1：主干宽为1 mm、两侧枝长为3.50 mm、主干枝长为9.6 mm、两侧枝宽为1.300 mm、主干与两侧枝的距离为4 mm;样本2：主干宽为5 mm、两侧枝长为0.75 mm、主干枝长为15.0 mm、两侧枝宽为0.175 mm、主干与两侧枝的距离为6 mm;此外，其他三层的厚度、长度、宽度等参数一致。

基于上述内容设置的参数，所仿真的电磁超材料中微波吸波体结构模型电流图如图2所示。

由如图2所示的电流图可知，不同结构参数的微波吸波体吸收电磁波后，所产生的电流密度、方向均不相同，而电流与电磁谐振具有如式（6）所示的关系：

（6）

其中，Φ表示电磁谐振波动强度;Q表示磁感应强度;β表示磁感应强度方向与电流方向的夹角。

借助如式（6）所示的关系式，就可以根据微波吸波体结构参数变化对电流造成的影响，确定微波吸波体结构参数对电磁谐波造成的影响。基于此，推断出微波吸波体结构参数会影响电磁谐波波动频率、波动和吸收率。

2  微波吸波体结构参数对电磁谐振的影响验证

为了验证此次研究的电磁超材料中微波吸波体结构参数对电磁谐振的影响程度，设计微波吸波体结构参数对电磁谐振的影响验证试验。

2.1  微波吸波体结构

此次试验主要选择树枝型、米字型、风车型三种微波吸波体结构。此次试验选择的微波吸波体结构均包括基层、介质层、损耗层和上层四个层次。其中，基层由硅组成，介质层和上层均由金属组成，损耗层由氟化镁组成，这四层的基础参数如表1所示。

2.2  试验过程

根据此次试验选择的三组不同结构参数微波吸波体，让电磁波按照垂直入射的方式摄入微波吸波体中，通过计算微波吸波体雷达散射截面，检测三组不同微波吸波体产生的谐振频率，以此确定微波吸波体结构参数对电磁谐振造成的影响。

2.3  计算雷达散射截面

虽然此次试验中的电磁波是从一个角度和一个点照射微波吸波体，但是微波吸波体在吸收电磁波时却会产生散射現象，即微波吸波体受到电磁波照射后，电磁波本身的能量会朝各个方向散射。此时，微波吸波体上就会生成由入射场和散射场构成的空间总场。依据“散射能量在空间中的分布取决于物体的结构参数以及入射波参数”这一理论，通过观察雷达散射截面来确定微波吸波体吸收电磁波时，所产生的电磁谐振变化。

基于此，需要先确定平面波的入射能量密度m1和散射能量密度m2，以及微波吸波体所接收到的总功率P，从而得到雷达散射截面这一度量值，公式为：

（7）

其中，B表示雷达散射截面;E1表示散射强度;E2表示入射强度。

依照式（7）所示的计算过程，就可以得到微波吸波体雷达散射截面值，判断微波吸波体吸收到电磁波后其不同层次产生的变化，以此得到电磁谐振频率值。

2.4  试验验证结果

将电磁波以垂直入射的方式正入射在微波吸波体10 GHz位置，所得到的试验结果如表2所示。

由2可以看出，在不同的γ角，三种微波吸波体正入射10 GHz的吸收峰外时，所得到的雷达散射截面值仅在-180°与180°处出现了完全重叠，其他角度完全不一致。

为进一步确定微波吸波体结构参数对电磁谐振的影响，将根据如表2所示的微波吸波体雷达散射截面对比图，统计三种微波吸波体垂直极化和水平极化时分别出现的谐振频率，统计结果如表3所示。

基于表3所示的统计结果，结合表2所示的雷达散射截面对比图可知，树枝型微波吸波体不具有中心对称结构，会出现明显的峰值，并不具备明显缩减雷达散射截面的功能，所产生的电磁谐波难以被其吸收;米字型微波吸波体呈中心对称结构，其在工作时所具有的工作频带宽于其他微波吸波体结构的工作频带，可以完美地吸收正入射10 GHz的电磁波，具有极化不敏感的吸波特性;风车型微波吸波体虽然也呈对称结构，但是其在工作过程中所产生的工作带宽会小于米字型微波吸波体结构，这就会导致电磁波的入射峰值随入射角的增大而减小，出现中心频率小幅右移现象。因此，树枝型微波吸波体不具备隐身性能，会对电磁谐波产生反射和散射影响;米字型微波吸波体吸收入射电磁谐波时，其产生的电磁波动一致，强度几乎相同，可以在吸波体上层结构内部形成电流环路，产生良好的阻抗;风车型微波吸波体则会提高电磁波的吸波率，但不会对超宽带的性能造成影响。

由此可见，树枝型微波吸波体的枝干会与电磁谐波产生强烈的耦合，增加吸波体对电磁波的吸收与损耗，从而改变电磁谐波波动频率;米字型微波吸波体可以完美地吸收电磁波，基本不会对电磁谐振造成影响;风车型微波吸波体在工作过程中产生的电磁谐振频率波动较小，能产生良好的阻抗，所具有的宽带吸波能力，可以从不同的角度通过不同的方式吸收电磁波，降低电磁谐振波动。因此，微波吸波体结构参数会影响电磁谐波的波动频率、波动和吸收率，与此次研究成果一致。

3  结  论

在此次研究中，将微波吸波体最上层金属膜的结构参数，作为微波吸波体重要结构参数，并以最上层金属膜结构参数变化对电磁谐振造成的影响，作为微波吸波體结构参数对电磁谐振的影响。经过一系列的计算和仿真，推断出不同结构参数的微波吸波体会改变电磁谐振波动频率、波动和吸收率，并采用试验的方式验证了此次研究成果。然而，此次研究仍然存在一定的不足，在今后的研究中，应该逐层研究微波吸波体不同层次的结构参数对电磁谐振所造成的影响，以期为微波吸波体的研究提供更多的依据。

参考文献：

[1] 孙磊，孙俊，高晓梅，等.基于超材料的微波宽带完美吸波体设计 [J].材料导报，2021，35（12）：12014-12019.

[2] 雷晓勇，霍树云，李燕，等.小型化超材料吸波体设计与电磁吸收分析 [J].电波科学学报，2021，36（6）：896-904.

[3] 吴雨明，丁霄，王任，等.基于等效介质原理的宽角超材料吸波体的理论分析 [J].物理学报，2020，69（5）：83-90.

[4] 曾宪亮，张麟兮，万国宾.一种基于有源频率选择表面的可调吸波体特性分析 [J].中国舰船研究，2020，15（2）：36-41.

[5] 王桂平，敖日格勒.Fe3O4/木质素基纳米碳纤维复合材料的制备及其微波吸收性能探究 [J].中国造纸，2020，39（5）：1-9.

[6] 王俊林，王鑫.基于Ⅰ型谐振结构的太赫兹超材料吸收体传感器研究 [J].传感技术学报，2020，33（7）：961-966.

[7] 张鑫，戴银所，崔传安，等.“兆”字型单层宽频电磁超材料吸波器仿真及分析 [J].电子世界，2021（20）：72-76.

[8] 王彦朝，许河秀，王朝辉，等.电磁超材料吸波体的研究进展 [J].物理学报，2020，69（13）：39-51.

作者简介：习柏林（1988.03—），男，汉族，湖北枣阳人，工程师，硕士研究生，研究方向：电磁场与微波技术。