优化习题教学 提升解题素养
2022-07-09淮北师范大学数学科学学院235000莫焕群广西民族大学数学与物理学院530006毋晓迪
淮北师范大学数学科学学院 (235000) 莫焕群广西民族大学数学与物理学院 (530006) 毋晓迪
1.引言
习题作为学生运用所学知识学以致用的重要资源,既是理解教科书并达到有效学习的辅助工具,也是评估学生学习目标是否达成的核心载体.当前习题课普遍存在的问题是,教师注重在自己的经验范畴内预设问题,忽视学生在问题情景中的真实想法.此外,习题教学方式单一,主要以“知识点+讲解”套解试题模式循环进行,长此以往,学生的学习目标难以落实到求是求真的层面,难以实现提升学生解题素养的目的.为此,要以培育和发展学生核心素养为着力点,需改观传统习题教学模式,重新定位习题教学目标.基于此,笔者以学生如何在习题教学中引发高阶思维活动,增强迁移应用能力,实现知识深度理解为导向目标,精准重组习题教学内容,合理选取教学方式,使习题教学成为促成学生发展数学学科核心素养的门径.
2.两种习题教学理论观点
在教育理论知识的学习和研究中,发现维果茨基认知发展理论说、布鲁纳的认知层次发现说等对本研究具有指导价值和意义.
一是维果茨基认知发展理论说.维果茨基认为人的认知水平可以划分为“已知区”、“最近发展区”和“未知区”三个层次.这三层次在学习活动中可以呈相互转化、螺旋上升态势.对于提出过易或过难的问题会减弱学生求知欲望的这一观念,需启发教师重点关注学生“已知区”与“最近发展区”的维系点.这一维系点即为知识的增长点,利于新知识的同化与完善学生的认知结构,使“最近发展区”化归为“已知区”.
二是布鲁纳的认知—发现理论说.如图1所示,布鲁纳将学生的行为从简到繁进行排序,并认为好奇心是学习的内在动力,其中直觉思维在学习活动中起到举足轻重的作用,并促使学习成为一个逐步探究的过程,同时提醒教师在教学中着重关注学生的信息加工和提取.
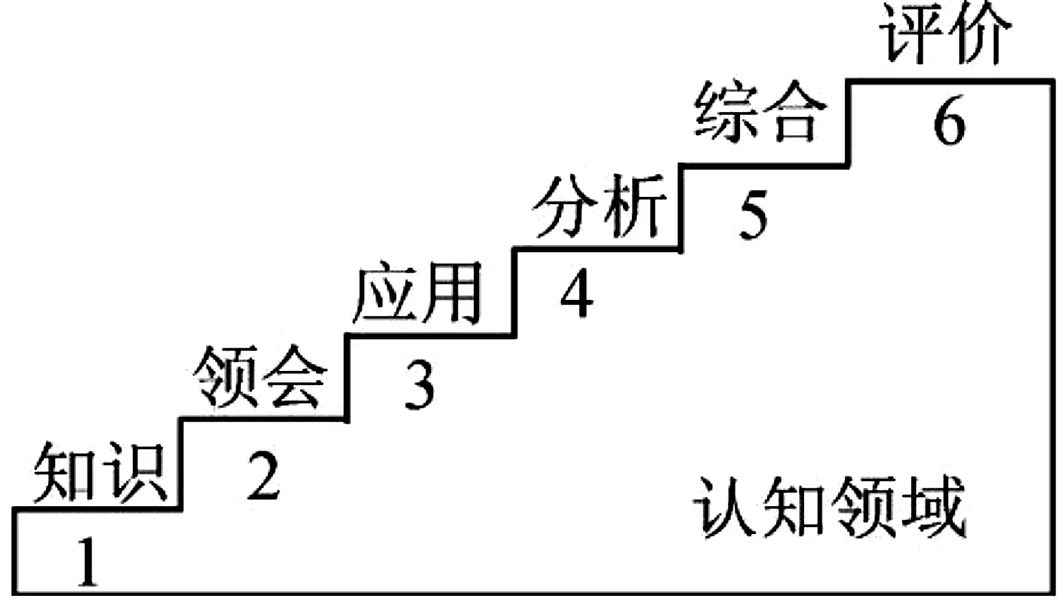
图1
3.优化习题教学对策
3.1 关注问题转化 引发高阶思维活动
学生在问题解决的过程中思维处于内隐状态,教师要有意引导学生挖掘问题的“题眼”,而学生对关键信息进行提取、分析、加工及表征等一系列操作,需要学生高阶思维深度参与.
例1 已知点P在直线l:x+y-3=0上运动,点O是原点,点B、C的坐标分别为(2,0)、(1,0),点A为坐标平面内一点,且有∠ACB=2∠AOB,求∠APC的最大值.
由题干信息作出直观图2,由关联条件并思考问题:如何转化关键信息∠ACB=2∠AOB?
此时,我们应该关注学生的“学”,窥视学生能否自主挖掘信息,由于点A是个动点,取不同位置时的点Ai(i=1,2,3,...),如图2所示,连接AO、AC,将新旧知融合关联,引导学生突破以下关键点:

图2 图3 图4
关键点1:∠ACB=∠AOB+∠CAO,得∠AOB=∠CAO,即|CO|=|CA|=1.
关键点2:|CA|=1,知动点A到定点C的距离为定长1,即点A只能在以点C为圆心,半径为1的圆周上运动,如图3所示.
再提出问题:点A是圆上的动点,点P是直线上的动点,它们分别运动到哪个位置时,∠APC的值最大?
关键点3:不论点A、P运动到哪个位置,∠APC一定是个锐角,采取“动”点A、“静”点P相结合思路,如图4,得到当AP与圆C相切时∠APC取得最大值.
自然得到问题:当点P在直线l:x+y-3=0上运动到哪个位置时,|CP|最小?

在本题的解析过程中,首先理清问题的来龙去脉,学生需要逐一突破关键信息,自然而然地把环环相扣的问题进行思路转化,融数、形、意三方面为一体来解决数学问题是高阶思维能力的直接体现,促进深度学习主动生成.
3.2 融合知识关联 增强迁移应用能力
一般地,在解决数学问题时,需要多知识点关联交汇.若知识关联程度较弱,不利于促进学生有效提取、挖掘、检索以及深加工关键信息.数学问题解决能力和迁移应用能力的培养与发展与数学认知结构的完善程度密切相关.换句话说,在习题教学时,通过问题解决窥视学生在知识关联程度上暴露出的认知缺陷,为完善认知结构,增强迁移应用能力起到助推作用.

本题以向量模长运算问题为落脚点,如何发掘并关联题干中给出的已知条件是本题的核心突破点,我们可以通过求向量模长设置问题情境.

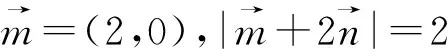
针对上述预设的问题,将挖掘并关联出的突破点逐一击破.
预设问题2:针对关键点1,接下来如何运算?对所求式子直接平方可以吗?

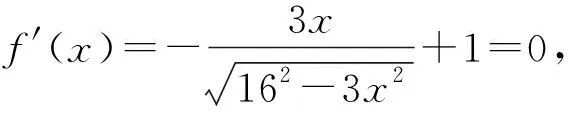
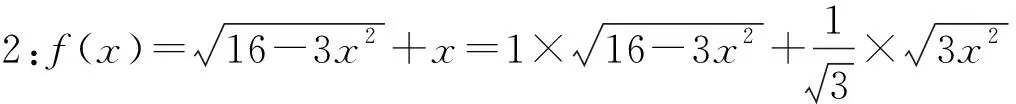
预设问题3:针对关键点2,你能快速运算求解吗?


通过本习题的预设的教学设计,在解决问题的的思维脉络上,选择出合适的起点,步步遵循学生思维规律,以向量模长运算为突破口,实现多知识深度关联,渗透转化与化归思想,通过不同角度描述向量模长,采取不同解法求解向量模长最值,让学生切身体悟基础知识深度转化与关联的价值.
3.3 聚焦模型建构 实现知识深度理解
数学模型的建构能力属于高阶思维能力.强化数学模型建构,推举教学目标进阶,有助于发展学生学科核心素养,有效培育学生综合分析能力,提升信息的重组与整合能力[1].
例3 在△ABC中,角A,B,C所对的边为a,b,c,BC=3,点D是边BC的一个三等分点,且∠BAC=60°,求AD的最大值.
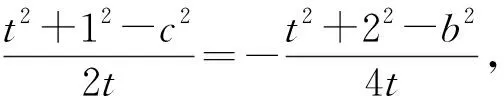
图5


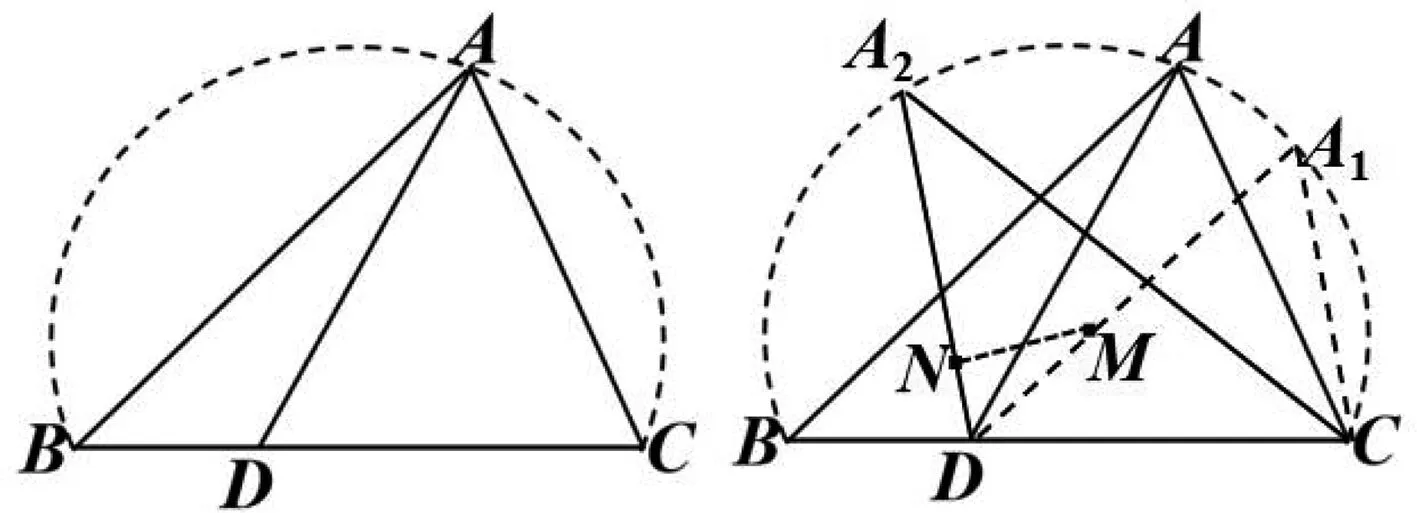
图6


图7
因此,在习题教学中,引导学生模型的构建要基于简化研究对象为原则,要关注研究问题的本质特征,我们是为了掌握基本解题方法而去建构模型,进而在学生可望又可及的认知范围内形成知识横向和纵向螺旋上升的立体结构.从而加深学生对知识的深度理解,促使牢固把握解题的通性通法.
4.习题教学启发与反思
4.1 分析问题时应培养学生有序逻辑推理习惯
在数学学习过程中,我们常会遇到题干抽象过程复杂的题目,如何寻求问题的突破口是解决问题的关键点,许多数学问题的解决需要综合运用数学知识推知与论证,并科学规范表达、运算,进而一步一步深入分析.习题教学中,思路自然清晰、富有条理是我们竭力追求的效果.为此,要使学生解题素养得以发展和提升,在习题教学中形成有序的解题思维,那么培养学生的有序逻辑推理习惯是必要的[2].笔者认为习题教学中,对于问题的解决的流程可以经历图8所示的步骤.

图8
4.2 解析过程应逐步深入聚焦问题本身
数学问题解决要从问题的本身出发,问题的本身就是思维的起点,也是教学活动中要进行启发、探究和设问等环节的出发点.例如阶段性考试,多数情况下是把刚学过系列知识“现炒现卖”,固然在短时间内能看到立竿见影的效果,但这与对知识的巩固路径不尽一致.
事实上,我们平时遇到的问题,尤其是综合复习阶段,不可能都是与我们刚学过的知识产生关联.为此,固定模式套解题的方式显然不可取,在分析问题的过程中,要从问题的本身出发,培养学生的动态思维,搭建问题解决的脚手架,并促使问题步步深入[3].唯有如此,学生思维的创新性才得以激发,对提升和发展学科核心素养具有促进意义.
4.3 解题步骤呈现应与学生思维同步
解题步骤的思维显化呈现,是直接作用于习题教学效果的评价.若教师在问题解决的过程中没有摸清学生的思路,“强制”要求学生按照自己思绪套路出牌,教学活动就会形成教师“一言堂”的态势,学生思维深刻性的培育便不可企及.
鉴于此,在习题教学中,对于解题步骤的探究论证,要联系学生的思维实际,揣摩学生心理状态,在启发中要与学生的思维同步,把握学生思维规律,预设学生在教学活动中可能凸显出的各种思维活动,给学生留出思考的时间并及时排除思路偏移,活化学生的动态思维.
4.4 解题方法选取应让学生感到可望可及
在习题教学中,多数教师青睐于运用多种方法达到问题解决的目的,启发学生从不同角度思考问题,进而提高思维发散性与求异性;提高问题解决的应变与贯通能力,加深对数学概念、定理等的理解与深化运用.
而我们在习题教学时,常遇到教师讲授了多种问题解决的方法和思路,但是学生也感叹:“这样的解题方法我想不到”,如果教师中断解释或者避开深入讨论某些解题方法,那么习题教学就会变成“走马观花”式罗列解法的教学.因此,习题教学的方法应考虑学生认知规律,避免为追求习题解题的深度而超出学生自然而然地接受知识的范畴,应适可而止,使学生切身感悟到方法可望又可及,方能有所知、有所悟,这样一来,习题教学的课堂生成会主动达成.
