并联式六维加速度感知机构的最大工作频率*

史浩飞尤晶晶陈华鑫

(1.南京林业大学机械电子工程学院，江苏 南京 210037；2.南京航空航天大学江苏省精密与微细制造技术重点实验室，江苏 南京 210016)

工作频带是衡量加速度传感器性能的重要指标之一，反映了其检测性能和适用场景。 对于一维加速度计而言，其工作频率的下限由相连电荷放大器的下限截止频率决定，一般可低至0.3 Hz[1]；其工作频率的上限一般取其基频的1/5～1/3[2]以避免感知机构发生共振[3]从而影响正常检测。 对于低维运动感知机构，对它的研究主要侧重于工作频率与传感器结构参数之间的关系。 Lee 等人[4]利用元模型分析了共振情况下，压电式加速度传感器的敏感参数的特性。 LIU 等人[5]基于一种折叠式横梁的压电式加速度传感器，研究了中心质量块的位移与工作频率之间的关系。 此外，针对静态或准静态加速度的特性，Lu 等人[6]研究了压电式加速度传感器在低频范围内的补偿方法，从而大大提高了传感器在低频范围内的测量精度。

与少自由度运动感知机构相比，六维加速度感知机构具有信息获取更全、测量精度更高、体积和成本更低等优势[7]，在航空航天[8－9]、振动测试[10]等领域应用前景广阔。 对于该类感知机构，其最小工作频率由电荷调理仪器的性能决定，而最大工作频率的界定尚未解决。 目前，六维加速度感知机构的固有频率等特性已得到了深入研究[11－13]，因此以固有频率为切入点是进一步探究最大工作频率的有效途径。

鉴于此，本文首先基于第二类Lagrange 方程建立了感知机构的无阻尼自由振动微分方程，并利用Householder 法和单步QR 法求解了振型方程的特征值问题；利用软件仿真，验证了基频模型和方程求解的正确性；最后，研究了六维加速度感知机构的基频与最大工作频率之间的线性关系。

1 基频模型

并联式六维加速度感知机构由质量为m、边长为2n的正方体质量块及长度为l的支链构成。 图1为三种感知机构的结构简图，其构型分别为9－3、12－6和12－4。 以12－4 构型为例，其中Bij(i＝1，2，3，4；j＝1，2，3)表示与基座固连的一般球铰链，bi(i＝1，2，3，4)表示与质量块固连的复合球铰链，Pij(i＝1，2，3，4；j＝1，2，3)表示各支链上的压电陶瓷。 分别在质量块和基座上建立笛卡尔坐标系O1－X1Y1Z1、O2－X2Y2Z2，分别记为{U}和{L}。 动平衡状态时两坐标系的原点重合于质量块的质心处，其坐标轴分别与质量块的三条棱边平行。

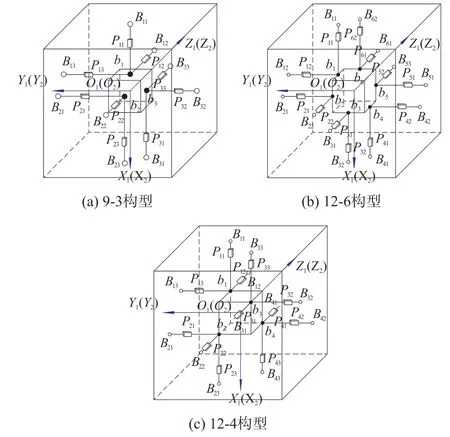
图1 并联式六维加速度感知机构的结构简图

1.1 建立支链的运动学方程

复合球铰链在{L}系中的坐标b{L}i可表示为:

式中:O{L}表示{U}系的原点在{L}系中的坐标；R{L}表示{U}系相对于{L}系的旋转矩阵；为复合球铰链在{U}系中的坐标。

因此，该感知机构支链的运动学方程为:

式中:lij表示各支链的矢量；表示基座上的一般球铰链在{L}系中的坐标。

1.2 建立无阻尼自由振动微分方程

利用四元数来描述{U}系相对于{L}系的姿态，则{U}系相对于{L}系转动的角速度矢量ω{L}可表示为[7]:

式中:λ0为该四元数的实部元素；λ1、λ2、λ3分别为该四元数的三个虚部元素；̇λ＝[̇λ1，̇λ2，̇λ3，̇λ0]T。

根据第二类Lagrange 方程，系统无阻尼自由振动微分方程的标准表达式为:

式中:Ek表示质量块的动能；Ep表示压电陶瓷的弹性势能；qj表示系统的广义坐标[14]，q1～3为描述{U}系相对于{L}系位置坐标的三个分量，q4～6分别等于λ1，λ2，λ3。

式(2)中质量块的动能函数可表示为:

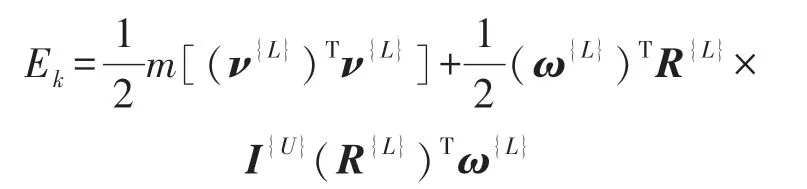
式中:ν{L}表示{U}系的原点相对于{L}系移动的线速度矢量；I{U}表示质量块在{U} 系中的惯性矩阵[7]:

故质量块的动能函数可近似表达为:

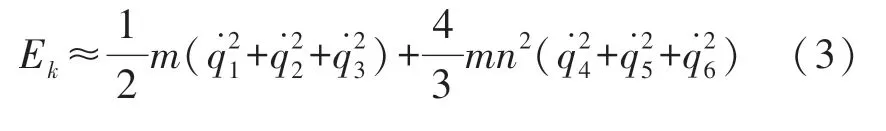
式(2)中压电陶瓷的势能函数可表示为:

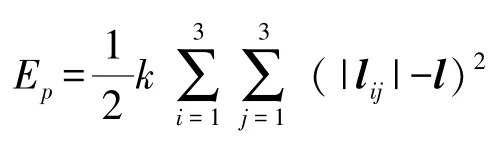
式中:k表示压电陶瓷的等效刚度。

根据泰勒公式展开并忽略二阶以上无穷小量，结合式(1)整理可得广义坐标形式下的势能函数:

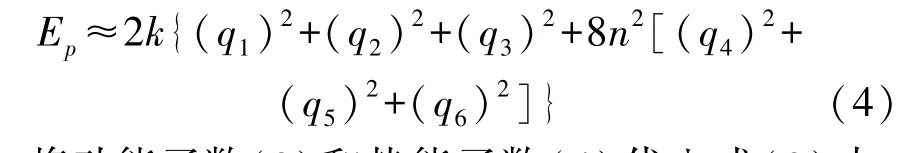
将动能函数(3)和势能函数(4)代入式(2)中，整理可得12－4 构型六维加速度感知机构的无阻尼自由振动微分方程:

式中:M、K表示六维加速度感知机构系统的质量矩阵和刚度矩阵；表示广义加速度；0 表示六阶零矢量，且:

2 基频的求解及算例验证

2.1 特征值问题的分析

式(5)的解对应着系统的无阻尼自由振动，由于不存在能量的损失，系统将永不停歇地振动下去。假设所有的坐标作同步运动，即两坐标间的振动位移之比恒定，则设该方程的解为:

式中:Qi为常数；T是时间t的函数。

将式(6)代入式(5)并展开为方程组形式，可得:

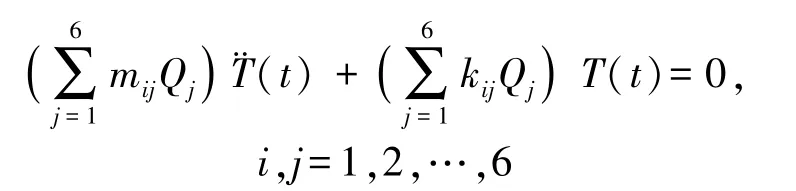
式中:mij，kij分别表示质量矩阵和刚度矩阵中的对应元素。

故而可得到如下关系:

式(7)等号右边为常数，与时间t无关，令其等于ω2，则式(5)可改写为:

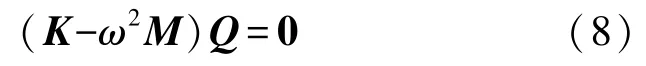
式中:ω为系统的固有圆频率。

又因Q不为零，故有:

式(8)表示一特征值问题，式(9)为其特征方程，ω2为其特征值。 令ξ＝1/ω2，定义动力矩阵D＝K－1M，则式(9)可转化为:

2.2 特征值问题的求解

对于并联式六维加速度感知机构这类多自由度系统，通过求解多项式方程来获得动力矩阵D特征值ξ的过程是十分繁琐的。 鉴于此，可利用Householder 法[15]和单步QR 法[16]来对特征值问题进行求解。

设:

根据Householder 法，将动力矩阵D转化为上Hessenberg 矩阵H，其形式如下:

再根据单步QR 法，对H进行迭代运算，将其变换为对角矩阵H′，并按升序重新排列其对角线元素，即有:

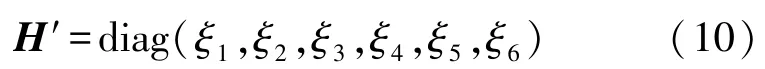
式中:ξ1～6为动力矩阵D的特征值。

根据固有圆频率与频率之间的关系，六维加速度感知机构系统的基频f0可表示为:

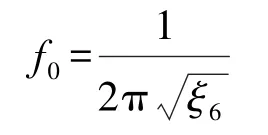
由式(10)可以看出，感知机构的高阶固有圆频率也已在迭代过程中求出，故高阶固有频率也可同时计算得知。 对于感知机构的各阶振型向量，可利用已知的ξ值根据反幂法求解，这里不再进行讨论。

2.3 算例验证

以动力学仿真软件ADAMS 为参考，首先对上述建立的12－4 构型感知机构的基频模型进行算例验证。 取质量块的边长为0.040 m(质量块的质量为0.499 264 kg)，支链刚度为2×108N/m，得到其各阶固有频率。 根据图2 所示，该系统的基频为6 370.888 4 Hz。 随后，基于本文1.2 节的推导结果和矩阵迭代法[7]编写程序，计算得出基频值为6 370.888 4 Hz。

图2 12－4 构型六维加速度感知机构的基频

鉴于9－3 构型的质量矩阵和刚度矩阵均为非对角阵，具有普遍性，这里再以该构型为例验证2.2节的求解过程。 同样以上述参数为例建立系统的动力学模型，分析其基频。 图3 显示了该系统的基频仿真结果，可以看出其值为2 985.969 0 Hz。 随后，基于9－3 构型的无阻尼自由振动微分方程和本文2.2 节的解法编写程序。 其中，Householder 法经过了4 步运算，单步QR 法经过了如图4 所示的11 次迭代，完成了各阶固有频率的计算，显示其基频为2 985.969 0 Hz。

图3 9－3 构型六维加速度感知机构的基频

图4 9－3 构型各阶固有频率的迭代过程

上述两例的验算结果均与动力学仿真的结果吻合，这验证了振型方程的正确性。

3 感知机构最大工作频率的确定

为确定感知机构的基频和最大工作频率之间的关系，需要建立具有不同基频的感知机构动力学模型。 通过改变影响感知机构基频的两个因素，即质量块的质量和支链的刚度，分别建立了不同参数的9－3、12－6 和12－4 构型感知机构模型，并利用ADAMS 仿真得出其最大工作频率的准确值。 各构型的模型参数取值与最大工作频率数据如表1、表2和表3 所示。

表1 9－3 构型的模型参数及最大工作频率 单位:Hz

表2 12－6 构型的模型参数及最大工作频率 单位:Hz

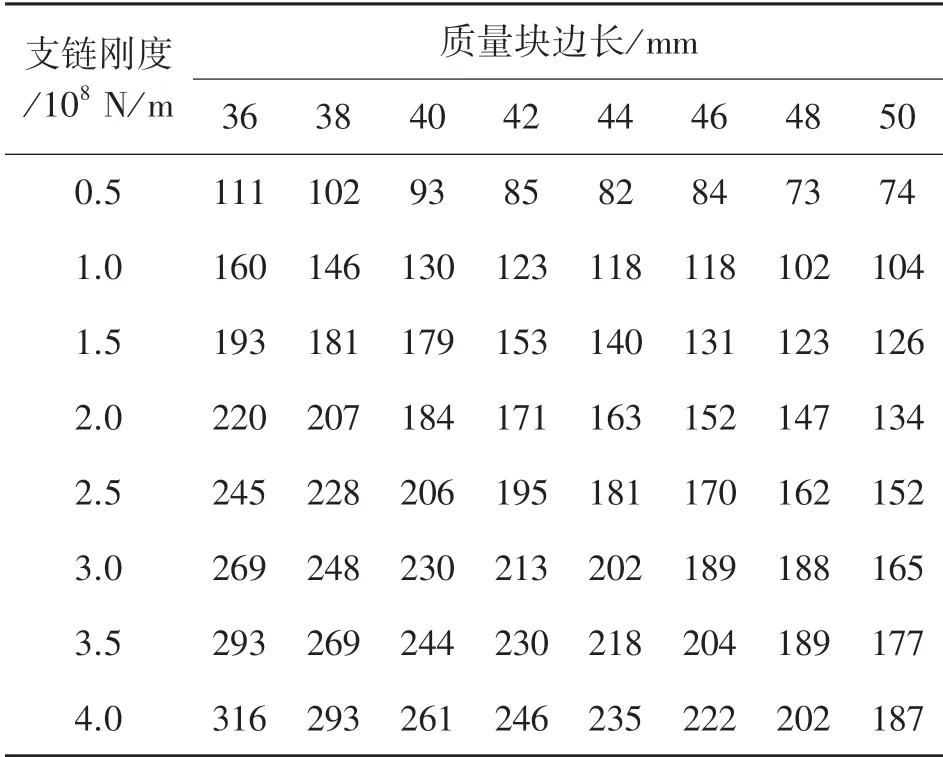
表3 12－4 构型的模型参数及最大工作频率 单位:Hz

对表1、表2 和表3 中的数据进行线性拟合，设拟合曲线为Fmax＝hF0，其中Fmax表示动力学仿真得到的最大工作频率；F0表示感知机构的基频；h表示拟合曲线的斜率。 各构型拟合出的参数如表4 所示，拟合效果如图5 所示。

进一步利用包络线理论分析最大工作频率与基频之间存在的线性关系。 设:

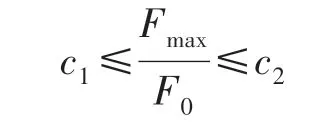
式中:c1、c2分别表示下包络线和上包络线的斜率，且要保证(c2－c1)最小。

利用上述拟合方程对9－3、12－6 和12－4 构型各自的64 组仿真数据进行包络拟合，拟合效果如图5所示，拟合参数如表4 所示。

图5 最大工作频率与基频间的拟合关系

根据表4 的包络线斜率可以发现，六维加速度感知机构的最大工作频率与其基频之间近似满足线性映射的关系，且不同构型所对应的比例系数差异不大。 另外，表4 列出了三种构型感知机构的几个重要物理函数/矩阵的解析表达式。 基于此，将有利于进一步剖析该类系统的解耦机理。

表4 各构型感知机构的物理函数/矩阵对比

4 总结

本文根据第二类Lagrange 方程建立了并联式六维加速度感知机构的无阻尼自由振动微分方程，据此求解了系统的质量矩阵和刚度矩阵，从而建立了基频模型。 利用Householder 法和单步QR 法求解基频模型的特征值问题，准确得出了基频值。 为了分析最大工作频率与系统基频之间的关系，对影响感知机构基频的两个分量进行了分析，拟合结果表明，该类系统的最大工作频率与基频的比值在0.029 36 左右，最大工作频率的波动范围处于基频的[1/36，1/30]区间内。