基于改进卡尔曼数据融合算法的温室物联网采集系统研究*
2022-07-09李少年李毅魏列江李金平杨攀包尚令
李少年李 毅魏列江李金平杨 攀包尚令
(兰州理工大学能源与动力工程学院,甘肃 兰州 730050)
农业现代化是国家现代化的基础和支撑,目前仍是我国农业发展的突出短板,发展设施农业是实现现代化农业的重要途径之一,而温室大棚则是设施农业的重要组成部分[1]。 温室是一个内部参数时刻在动态变化着的系统。 温室中的空气温湿度、二氧化碳浓度、光照强度、土壤湿度等环境因素与作物的生长情况密切相关[2-4]。 同时,温室也是一个多变量、非线性的不确定系统[5],因此,对环境参数的精确采集就显得尤为重要。
利用物联网实现信息采集和传输的技术已经日渐成熟,将ZigBee 无线传感网络应用在温室控制系统中已成为大量学者的研究方向之一[6-8]。 无线传感技术可节省线缆、变送器和采集卡等硬件设备,而且具有功率小、可靠性高的特点[9],它对单个节点的精度要求不高,同时也增强了系统的容错性。
我国大多数地区温室数据采集的方法比较落后,存在设施结构简单、采集精度低等问题。 一些发达国家如日本、荷兰、美国等在温室研究方面取得了显著的成果,采取多传感器数据融合的方法,对采集到的环境信息通过多种途径进行融合,有效地提高了数据的传输效率和信息的准确性[10]。 张平川等人[11]设计了卡尔曼滤波、欧几里德距离公式及多元聚类统计相结合的多传感器数据融合算法,这种方法对传感器的分组方式依赖较强,分组不同,数据融合的结果不同,误差也会不同。 王振等人[12]提出了一种基于狄克逊准则的卡尔曼数据融合算法,但狄克逊准则的计算量较大,会导致系统功耗增大。 高昕等人[13]在采集参数时引入了卡尔曼滤波器,对数据进行实时动态处理,每次滤波只进行一次卡尔曼循环,只能有限地减少误差,且未考虑传感器故障等情况。 目前多传感器数据融合的方法有加权平均法、贝叶斯估计法、D-S 论证法、卡尔曼滤波法、模糊逻辑推理法等[14-15]。
另一方面,由于温室面积较大,同一环境参数需要在不同区域布置多个传感器来进行检测,因此会存在大量传感器冗余数据。 当因传感器精度不高而导致误差较大或测量波动明显时,会直接导致系统的控制效果不佳。
基于以上分析,本文研制了一种基于改进卡尔曼数据融合算法的温室物联网采集系统,借助传感器技术、ZigBee 技术和卡尔曼滤波技术对各类传感器测得的数据进行采集、传输和融合处理,在此基础上可提高系统的控制精度,是一种高效的温室数据采集模式。
1 系统总体设计
1.1 系统框架
数据采集系统的总体框图如图1 所示,系统整体框架分为三部分:ZigBee 无线传感模块、STM32 主控平台模块和远程监控模块。 系统选用DHT11 空气温湿度传感器、GM5516 光敏电阻、SGP30 气体浓度传感器和KTR-TW 传感器,分别对温室中的空气温湿度、光照强度、二氧化碳浓度和土壤湿度进行检测。
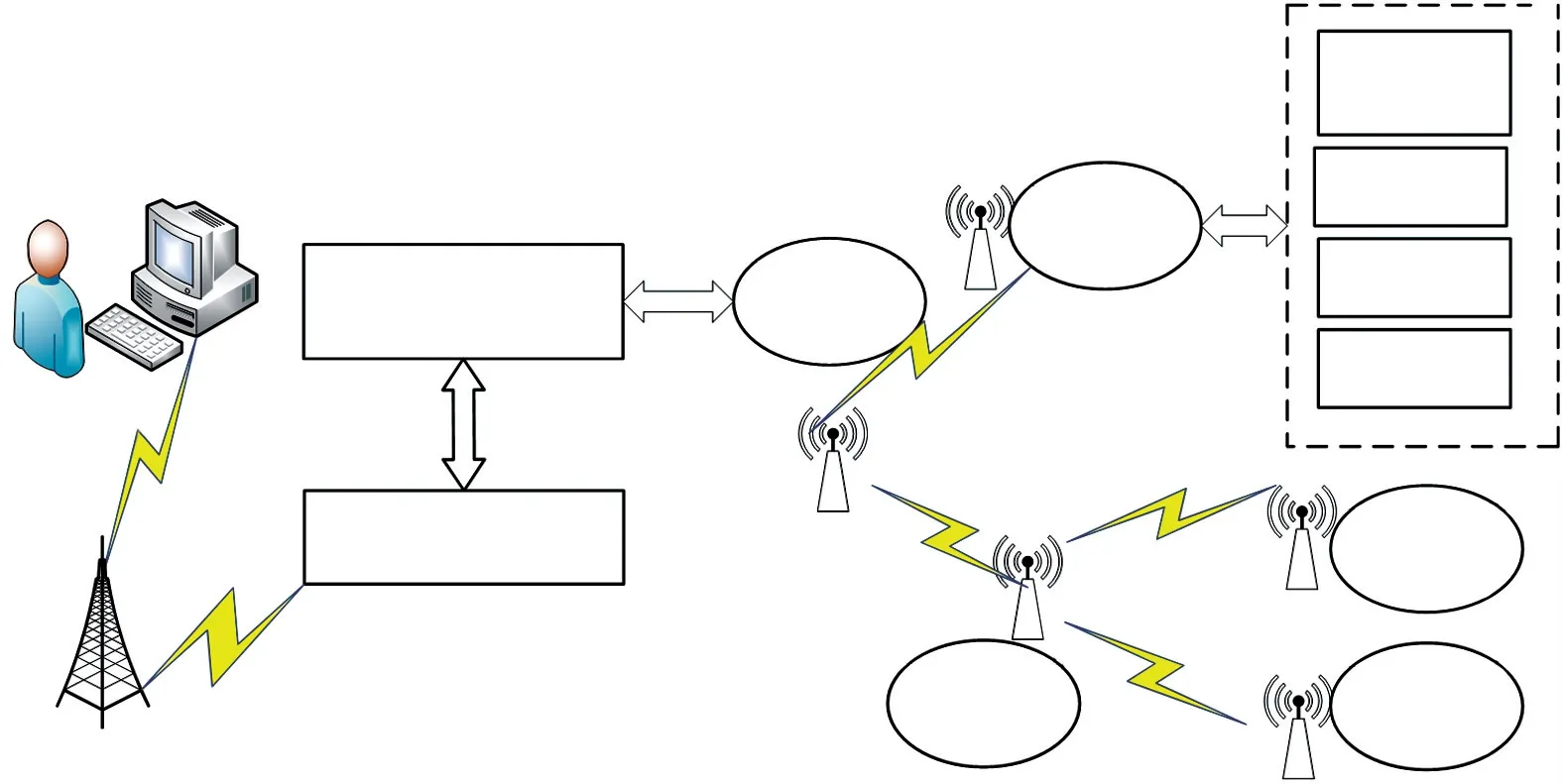
图1 数据采集系统的总体框图
数据采集的流程为:各类传感器分别对温室中的空气温湿度、光照强度、二氧化碳浓度和土壤湿度进行检测,通过串口将测得的数据上传给ZigBee 终端节点,ZigBee 终端节点再将数据通过路由器中转发送至协调器,协调器将数据进行处理、打包并上传给STM32 微处理器,STM32 微处理器对数据进行一系列有规律的存储和分析后,通过TCP/IP 协议将数据信息传递给上位机端,在上位机界面上进行显示,这样,操作人员可直接监测温室内各类参数的变化,并且可以进行适当的调控。
1.2 系统软件开发
系统的软件设计分为ZigBee 无线传感网络的软件设计、STM32 主控平台的软件设计和远程监控端的软件设计三部分。
选择Keil5 软件作为ZigBee 无线传感网络节点的开发平台。 ZigBee 终端节点负责对温室内的环境参数进行采集,根据传感器自带的数据手册,可将程序移植到APP 层,使用Z-Stack 提供的API 工具对函数进行调用后,在Keil 软件中进行程序的调试,Keil调试程序如图2 所示。 为减少系统的功耗,将终端节点的唤醒周期设置为15 min,即每15 min 进行一次数据的采集与上传,在工作周期外终端节点为休眠状态。 终端节点的工作流程为:初始化终端节点后加入协调器网络,在工作周期内,每15 min 调用一次GetTemp( )函数用来采集各类传感器测得的环境参数,将数据进行封装后发送数据帧到路由器或协调器。 ZigBee 协调器是整个ZigBee 网络的核心,它负责组建网络、接收各个节点发送的数据、处理数据并通过串口上传给STM32 微处理器。 协调器节点的工作流程为:系统初始化后进行通道扫描,当有空闲通道时,给其配置网络参数并组建网络,在此之后进入监控状态,随时等待节点申请入网或对终端节点发送的数据进行接收,若收到数据,则将数据运用其内置算法进行处理后打包发送给主控制器。

图2 Keil 调试程序
STM32 主控制器是主控平台的核心,选择Keil5作为它的软件开发平台。 STM32 主控制器软件在设备上电后进行串口和环境调控的初始化,串口1收到协调器节点发送的数据后将其上传给主控制器,当数据超出系统在远程监控端设定的阈值时,STM32 控制继电器动作。 数据封装后通过4G 模块发送给远程监控中心,监控中心通过控制继电器动作对环境进行调控。
采用NI 公司研发的LabVIEW 软件进行PC 端的上位机程序开发,它是一个面向最终用户的工具,使用图形化的编程方式,易学习且功能强大。 程序设计包括登录界面、用户管理、密码修改、参数设置、继电器动作、实时数据显示、历史数据查看等功能,LabVIEW 程序开发如图3 所示。
图3 LabVIEW 程序开发
1.3 系统硬件开发
在温室中,ZigBee 模块的协调器、路由器、传感器和主控制器等部分构成了系统的硬件平台,对系统硬件部分的设计应遵循稳定性高、功耗低的条件。
使用Altium Designer 软件进行系统硬件电路设计。 ZigBee 的硬件包括传感器模块、CC2530 芯片、电源和频射天线等部分。 STM32 主控平台的硬件结构包括晶振电路、电源稳压电路、电源滤波电路、JLINK 接口电路、BOOT 选择电路、USB 接口电路、复位电路等。 在选择STM32 芯片时,需考虑系统的整体功耗大小、成本高低和开发周期的问题,本次设计选择STM32F103C8T6 芯片,它具有丰富的I/O 接口,支持多路串行通讯,可满足设计需求。
2 数据预处理
传感器在工作时可能会出现故障,导致测量数据异常而携带粗大误差,严重影响了数据融合结果的精度[16-18]。 因此,需要对初始数据进行预处理,剔除对系统造成影响的粗大误差。
判别粗大误差常用的方法有罗曼诺夫斯基准则、格罗布斯准则和狄克松准则等[19],本次研究选择罗曼诺夫斯基准则来判别粗大误差,它适合在采样次数较少时使用。 罗曼诺夫斯基准则又称t检验准则,用于测量次数在4~30 次之内的测量过程,其特点是先剔除一个可疑测量值,然后应用t检验准则来检测这个可疑值是否包含粗大误差,判断过程如下:
对某个量进行多次独立的等精度测量,测得结果为:

若认为测量值xj为可疑数据,则将其剔除,即xj不参与计算,其余测量值的平均值:
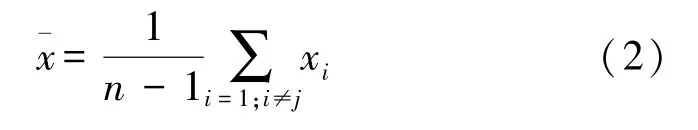
设第i次测量结果的误差vi=xi-,则利用贝塞尔公式计算测量结果的标准差为:

根据测量次数n和选取的显著度α,通过查表法可获取t分布的检验系数K(n,α)的值,α取值一般为0.05 或0.01,表1 为检验系数K取值表,其中测量次数n的范围为13~20 次。

表1 检验系数K 取值表
若xj满足式(4)关系:

就认为第j次测量结果xj含有粗大误差,应该剔除,否则认为xj不含粗大误差,应予保留。 以此类推,可将每个测量参数逐个进行检验,直至测量数据组不再含有粗大误差为止[20]。
3 卡尔曼滤波
虽然进行了数据预处理,但由于无线传感器本身存在测量精度不高的问题,会产生测量误差,通过采集节点采集到的数据也存在着大量的数据冗余和噪声干扰[21-23],会使系统的控制精度下降。 卡尔曼滤波器是一种最优化递归数字处理算法[24-26],它十分适合使用在温室系统中,适合卡尔曼滤波算法的系统特点为:系统不存在完美的数学模型或系统模型难以建立、系统扰动是不可控的且系统中的传感器测量存在着误差[27]。 卡尔曼滤波器的状态空间方程如下所示:
状态方程:

观测方程:

式中:k为离散时间,X(k)为系统在k时刻的状态,Y(k)为系统在k时刻的观测信号,W(k)∈N(0,Q)为系统在k时刻的过程噪声,V(k)∈N(0,R)为系统在k时刻的观测噪声,U(k)为系统在k时刻的输入信号,A为状态转移矩阵,B为控制矩阵,Γ为噪声驱动矩阵,H为观测矩阵,P为协方差矩阵,R为观测噪声方差,Q为过程噪声方差。
卡尔曼滤波器的实现过程为:使用上一次的最优结果(k-1 |k-1)预测当前的先验值(k|k-1),同时使用当前的观测值Y(k)修正当前的先验值(k|k-1),得到当前的最优结果(k|k)。 卡尔曼滤波流程如图4 所示。

图4 卡尔曼滤波图示
式中:I为单位矩阵,K(k)为系统在k时刻的卡尔曼增益,(k|k-1)为系统在k时刻的先验值,(k-1 |k-1)为系统在k-1 时刻的最优估计值,(k|k)为系统在k时刻的最优估计值。
4 改进的卡尔曼数据融合算法
以温室中的温度作为观测对象,在测量时,由于人体干扰,阳光照射,风力干扰等因素,温室中的温度会存在波动,且温室中存在通风装置,会与外界产生空气流通和交换,在此过程中会存在过程噪声,方差为Q。 在传感器测量时,由于精度影响会存在测量误差V(k),方差为R。 由于温室中的温度变化为一维系统,即X(k)为一维变量,相应地A=Γ=H=1,系统无控制输入,控制量U(k)=0。 化简后,温室的状态空间方程为:
状态方程:

观测方程:
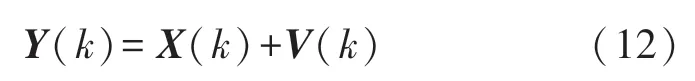
卡尔曼滤波器核心公式为:

4.1 方案分析与选择
本次方案分为两种:取一个传感器在不同的时刻对同一区域内的温度进行测量,使用卡尔曼滤波算法进行动态滤波,观察其误差情况;取一组传感器在同一时刻对同一区域内的温度进行测量,使用卡尔曼滤波算法进行静态滤波,观察其误差的情况。
选取温度作为观测量并使用MATLAB 软件进行编程和仿真,假设温室内的初始温度为24.5 ℃,室温内的期望温度为25 ℃,初始测量误差为2 ℃,卡尔曼滤波初始估计误差为5 ℃,由于温室是封闭的状态,与外界的能量交换十分微弱,取Q=0.01。查阅产品的说明书,DHT11 温度传感器的方差为0.25,即R=0.25。
将初始参数带入式(11)~式(17)中进行仿真,动态卡尔曼数据融合曲线如图5 所示,误差曲线如图6 所示。
由图5 和图6 可看出,在动态测量中使用卡尔曼算法进行滤波时的估计值和真实值较为接近,但温度误差的波动较大,多次达到了0.5 ℃。

图5 动态卡尔曼数据融合曲线

图6 动态卡尔曼数据融合误差曲线
取20 组传感器测量的温度数据进行静态的卡尔曼数据融合,测量数据为:[24.5 ℃;25.7 ℃;24.9 ℃;26.5 ℃;24.3 ℃;26.8 ℃;25.4 ℃;26.6 ℃;25.2 ℃;23.9 ℃;24.6 ℃;24.9 ℃;25.6 ℃;26.3 ℃;23.8 ℃;24.7 ℃;26.1 ℃;25.5 ℃;25.7 ℃;23.4 ℃]。 静态卡尔曼数据融合曲线和误差曲线如图7 和图8 所示。

图7 静态卡尔曼数据融合曲线

图8 静态卡尔曼数据融合误差曲线
从图7 可以看出,经过静态卡尔曼数据融合后,在第十次滤波后就得到了较为稳定的温度值,与真实值较接近。 由图8 可以看出,随着采样次数的增加,温度误差逐渐减小,最终接近0.1 ℃。 也就是说,随着测量次数的增加,测量结果逐渐趋近于真实值。
基于以上讨论,本系统选择多传感器在协调器端进行静态卡尔曼数据融合的方法。
4.2 改进的卡尔曼数据融合算法
卡尔曼滤波器会根据上一时刻的估计值和当前的测量值来估算下一刻的估计值[28-29],由此可以看出,当某个传感器出现故障而导致其测量值携带粗大误差时,会对卡尔曼滤波的数据融合的效果产生影响。
为了分析卡尔曼滤波算法受到含有粗大误差的数据干扰时的数据融合效果,在第7 次和第18 次测量结果中加入粗大误差,分别将25.4 ℃、25.5 ℃变为含有粗大误差的30.4 ℃、30 ℃后,再使用卡尔曼滤波算法进行数据融合,观察其数据处理的效果。
加入粗大误差时,得到的卡尔曼数据融合曲线如图9 所示,误差曲线如图10 所示。

图9 加入含粗大误差数据时卡尔曼数据融合曲线

图10 加入含粗大误差数据时卡尔曼数据融合误差曲线
由图9、图10 可以看出:在第7 组和第18 组数据含有粗大误差时,卡尔曼数据融合曲线和误差曲线均在7 次和第18 次测量后出现了较大波动,温度误差达到了1.1 ℃和0.86 ℃,最终的融合结果也受到了影响。 由此可以得出:携带粗大误差的测量数据会对卡尔曼滤波器的数据融合效果产生较大的干扰,应当剔除。
选取显著度α的值为0.05,检验系数K(0.05,20)=2.16,使用罗曼诺夫斯基准则对含有粗大误差的数据进行处理和滤除后,再使用卡尔曼滤波算法进行数据融合,得到滤除粗大误差前后的误差对比曲线如图11 所示。

图11 滤除粗大误差前后的误差对比
从图11 可以看出,使用改进的卡尔曼滤波算法进行数据融合后得到温度的误差由0.57 ℃降为0.089 ℃。 数据预处理的方法可以有效地解决测量数据携带粗大误差的问题。
5 实验验证
对甘肃省兰州市甲子山上搭建的温室大棚内的温度进行测量,测量时间选择为6 月份某天的7:00~14:00,DHT11 温度传感器每15 分钟测量一次温度值并通过ZigBee 无线通讯模块将测量数据传输给STM32 微处理器,STM32 微处理器再将数据传送给上位机进行显示。 实验测量图如图12 所示,远程监控界面如图13 所示。

图12 实验测量图
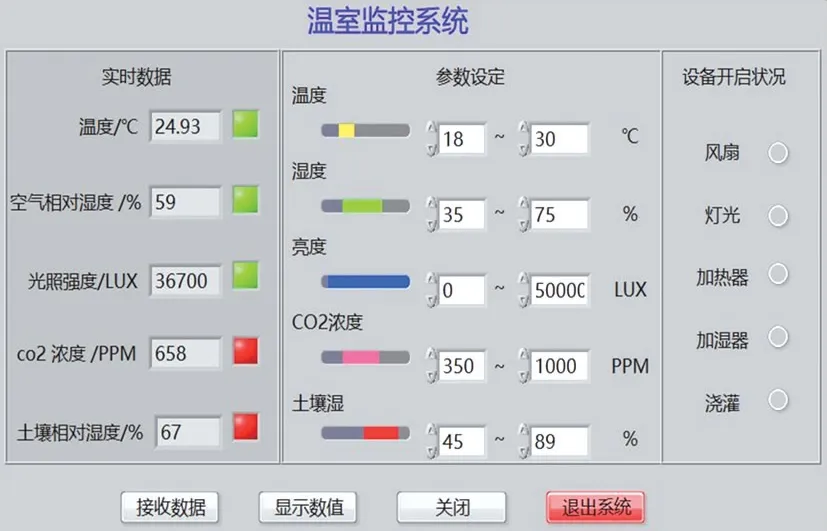
图13 远程监控界面
由于难以获得环境参数的真实值,选用Ametek公司的DTI-1000 数字测温仪测量的温度近似代替温室内温度的真实值,它具有低漂移校准性、可靠性好和准确性高的特点, DTI-1000 分辨率高达0.001 ℃,可用于验证任何类型的温度校准仪器的温度真值。
选取一组温室内DHT11 温度传感器测得的数据和在同一时间同一区域内使用DTI-1000 数字测温仪测量的数据,再将温度传感器测得的数据组经过预处理后使用卡尔曼滤波算法进行数据融合,得到一组新的数据,将这三组数据进行拟合,温度数据拟合曲线如图14 所示。
从图14 可以看出,将温度传感器测得的数据组经过改进卡尔曼数据融合算法处理后,与专业温度测量仪器测得的数值重合度很高,变化几乎一致。

图14 温度数据拟合曲线
为了验证处理结果的合理性,同时使用改进卡尔曼数据融合算法对温室中的湿度数据进行处理和拟合,得到的湿度数据拟合曲线如图15 所示。
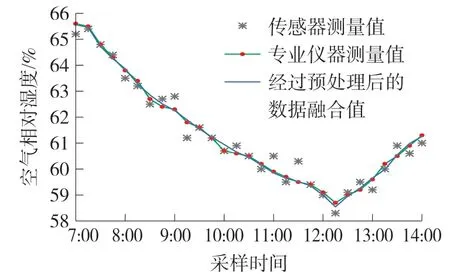
图15 湿度数据拟合曲线
由图14、图15 可看出,通过改进卡尔曼数据融合算法可有效地提高系统的采集精度,从而可提升系统的控制精度,有利于系统下一步的控制操作和执行操作。
6 结论
为解决传统温室中环境数据采集精度不高、能耗大、监测灵活度差等问题,本文研制了一种基于改进卡尔曼数据融合算法的温室物联网采集系统,具有功耗低、扩展性强、数据采集精度高等特点。 并针对数据预处理后的卡尔曼数据融合效果进行了仿真分析和实验验证,得到如下结果:
①使用罗曼诺夫斯基准则对测量数据进行预处理,去除数据组中含有粗大误差的数据,可以有效地解决传感器测量数据波动大的问题,对后续的操作起到了较好的预处理作用。
②对数据进行预处理后,再进行静态的卡尔曼数据融合,得到数据的误差更小,温度误差可减小到0.089 ℃,更加趋近于环境的真实值。
③通过对测量数据进行融合的方法,可有效减小传感器的冗余数据,降低系统功耗。
温室是一个多输入、多输出、多变量的系统,其中各类环境参数相互耦合,在本系统研究的基础上,下一步可研究将不同类别的测量数据如空气温湿度、土壤湿度、二氧化碳浓度等多种信息进行融合,只输出一个综合性的量进行调控,从而使系统的采集和控制更加精确和智能,系统功耗更低。
