计及响应度的电力用户互动潜力画像分析
2022-07-09梁纪峰范辉李顺胡文平李铁成杨军吴赋章
梁纪峰, 范辉, 李顺, 胡文平, 李铁成, 杨军, 吴赋章
(1.国网河北省电力有限公司电力科学研究院, 石家庄 050021; 2.河北省能源互联网仿真建模与控制企业重点实验室(筹), 石家庄 050021; 3.武汉大学电气与自动化学院, 武汉 430072)
随着售电侧逐渐开放以及综合能源的不断发展,能源市场的竞争力度日益激烈,把握海量电力用户的用电需求是电力企业提升服务质量、增强竞争力的关键[1]。同时,智能电网的建设要求提高电网运行灵活性,而海量电力用户负荷具有可平移性和可中断性[2],在电力系统大力推行需求侧管理工作、促进电力资源优化配置的大背景下,挖掘用户负荷需求响应资源,合理进行负荷引导与分配,有利于缓解电力供需矛盾[3]。然而,引导海量电力负荷参与系统运行调节存在两个主要难点以致用户用电需求和互动潜力难以刻画:其一,作为现实经济人,电力用户的用电需求对不同用电场景和时空电价呈现出较大差异;其二,海量电力用户用电数据呈现高维化。为了方便业务人员直观地掌握电力用户用电特性以及互动潜力,高效制定精准的负荷调控措施,需要从海量数据中挖掘电力用户用电特性(包含用户对不同时空电价的响应度)并通过画像进行展示。因此,通过以原始用电数据为基础构建电力用户画像可以再现电力用户的真实状态,有利于电力企业挖掘用户需求与价值、进行用户细分实施精准营销[4],其对于加强电网风险管控、把握规划方向具有积极作用。
目前,国内外对电力用户画像已经开展了初步研究,前期工作以文献[5-6]为代表,其主要目的是电力营销、电费风险防控、信用评价。为了充分调动需求侧资源,近年来的相关研究主要关注用户分类,便于分析电力用户用电行为和调控潜力。文献[7-9]利用不同的聚类技术将不同用电特性的用户进行分类,进而针对每一簇的典型负荷曲线进行用电模式分析。文献[10]通过定义反映电力用户不同特性的特征体系来描述用户的用电特征,由于标签体系较为复杂,并不利于用户画像的建立。建立用户画像的初衷是从海量的数据中提取有价值的信息,简洁、可靠地表达真实用户的用电特性。文献[4]从电量原始特征集中选择与用户类别相关性高且特征之间冗余性低的最优特征集来建立电力用户画像,但未能体现用户响应度以及用户互动潜力。文献[11]在电力用户特征选择过程中为剔除冗余特征,采用相关系数衡量特征间的信息,而该方法只对线性关系敏感。总的来说,现有电力用户画像文献存在以下不足:①只关注用户分类研究;②标签体系过于复杂,不方便建立用户画像;③构建的电力用户画像未考虑用户响应度,进而展现用户参与系统调节的互动潜力。
针对以上不足,提出一种计及用户响应度的电力用户互动潜力画像分析方法,通过定义一组考虑用户响应度的特征指标体系,并基于相关性特征优选策略进行所需特征的有效、精简选取,基于此建立用户画像。首先,为了反映用户响应度,在考虑分时电价作用下用户的响应状态,建立用户响应模型;其次,定义反映用户响应度的需求响应特征体系;接着,为了从反映用户响应度的特征体系中选择精简、可靠的特征指标,采用一种基于信息相关性的特征选择方法进行特征体系可靠地精简;最后,对已选择的特征量化打分进行用户画像展示。
1 用户响应模型
在需求侧响应手段中,分时电价是一种最常见的方式。由于用户类型差异以及价格水平不同,电力价格变化时电力用户用电需求变化具有较大不确定性[12],因此需要对用户用电需求响应度进行建模。
1.1 改进型电力需求价格弹性矩阵
根据经济学原理,通常采用商品需求价格弹性系数反映商品需求量对价格变化的敏感程度。电力是一种特殊的商品,电力需求价格弹性系数能够反映电力用户用电需求量对电价变化的敏感程度。由于每一个时段的电价改变不仅影响本时段的电力需求,而且还会影响其他时段的电力需求[13],故电力需求价格弹性系数分为自弹性系数与互弹性系数,两者定义式为

(1)
(2)
式中:eii表示需求自弹性系数;ΔQi表示i时段用户电量变化量;Qi表示i时段用户原始用电量;ΔPi表示i时段电价改变量;Pi表示i时段原始电价;eij表示需求互弹性系数;ΔPj表示j时段电价变化量;Pj表示j时段原始电价。
在传统的电量需求弹性矩阵中,i时段的需求电量变化量ΔQi是由i时段电价变化量ΔPi和其他时段j(i≠j)电价变化量ΔPj联合影响的。根据用户响应特性可知,i时段电价变化对i时段电力需求的影响显著大于其他时段电价变化对i时段电力需求量的影响。为了让模型更加贴近实际情况,引入权重系数来衡量不同时段电价改变对i时段电力需求的影响程度。权重系数定义为
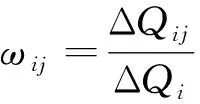
(3)
式(3)中:ωij表示j时段的电价改变影响i时段而产生的电量变化量,即ΔQij占i时段总电量变化量ΔQi的比例。
将灵活负荷的可转移时段长度L进行划分,然后每个时段的需求电量拆分,其表达式为
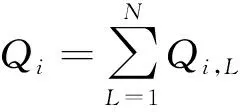
(4)
式(4)中:Qi,L为可转移时段为L的灵活负荷在时间段i内的电量需求。
在分时电价方式下,可转移时段为L的灵活负荷可以向电量需求弹性矩阵对角线侧转移,转移时段总长度为2L-1,故自、互弹性权重表达式为

(5)

(6)
式中:φi,L为可转移时段为L的灵活负荷在i时段内的电力需求占该时段总电力需求Qi的比例。
引入权重,修正后的自、互弹性系数的表达式为

(7)
则修正后的需求弹性矩阵可表示为

(8)
式(8)中:n表示用电数据时段数。
根据用户电量需求弹性系数表达式,可计算用户用电响应度,矩阵表达式为

(9)
1.2 需求响应特征指标
需求响应特征指标可以刻画用户响应度,即在分时电价作用下各类用户的响应程度和互动潜力,也可以表征用户响应后对用户负荷曲线移峰填谷的贡献度。为此本文中定义以下9个需求响应特征指标。
(1)峰荷减少率。

(10)
式(10)中:Qmax、Q′max分别表示用户响应前、后负荷的峰值。
(2)谷电系数率变化比。
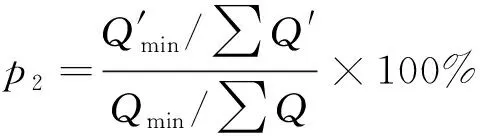
(11)
(3)需求响应潜力熵。根据信息论中信息熵的概念,定义电力用户需求响应潜力熵,它可以用来描述用户需求响应的潜力,其值越大,表明峰负荷曲线波动较大,其表达式为

(12)
式(12)中:n表示电力用户每日负荷采集次数,一般n=24;xi表示i时刻电力用户的原始负荷量。
(4)负荷率变化比。

(13)
式(13)中:Qave、Q′ave分别表示用户响应前、后的平均负荷。
(5)峰谷差率[14]。
(14)
式(14)中:Qmin、Q′min分别表示用户响应前、后负荷的谷值。
(6)峰时耗电率变化比。
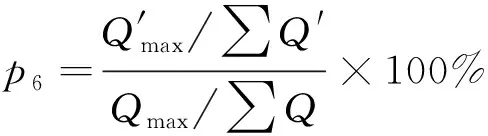
(15)
式(15)中:∑Q、∑Q′分别表示用户响应前、后总负荷。
(7)峰期负荷率变化比。
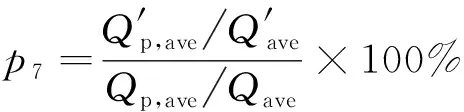
(16)
式(16)中:Qp,ave、Q′p,ave分别表示峰期平均负荷。
(8)谷期负荷率变化比。
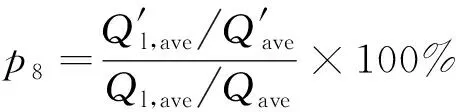
(17)
式(17)中:Ql,ave、Q′l,ave分别表示谷期平均负荷。
在构建用户画像过程中,反映用户互动潜力的需求响应指标众多,可能存在冗余特征,难以精简地体现用户互动行为,且用户互动潜力的画像本质是特征选择。在定义并计算各个需求响应指标值后,为建立用户真实互动状态的虚拟模型,需要进一步进行特征选择。
2 基于相关性的特征选择原理
基于相关性的特征选择原理[15]是一种启发式和过滤式相结合的方法,其核心思想是通过最佳优先搜索策略[16]生成特征子集,利用相关性矩阵计算该特征子集的评价值,选择评价值最大对应的特征子集作为最优特征子集组合。整体框架流程如图1所示。
2.1 计算相关性
首先,计算相关性矩阵。需求响应特征与电力用户类别之间以及不同需求响应特征之间的相关性是以信息熵[17]作为衡量标准,表示的意义分别为已知该需求响应特征时电力用户类别的不确定性减少程度和已知需求响应特征时另一个需求响应特征指标不确定性减少程度。在计算过程中,为了让每个需求响应特征更具有统计学意义,先将其值归一化处理,然后将特征变量区间离散化,从而得到各个需求响应特征变量的概率分布,最后完成需求响应特征与电力用户类别以及不同需求响应特征之间的相关性衡量标准——信息熵的计算。

图1 需求响应特征选择的整体流程Fig.1 The overall framework process of demand response feature selection
根据信息论,熵是不确定性的度量标准,变量Y的熵的定义式为

(18)
式(18)中:Y表示y所有可能的取值情况;p(y)表示y具体取值情况发生的概率。
在给定一个变量Y的条件下,另一个变量X的条件熵为

log2[p(y|x)]
(19)
式(19)中:X表示x所有可能的取值情况;p(x)表示x具体取值情况发生的概率;p(y|x)表示在x确定的条件下,y具体取值情况发生的概率。
信息增益表示变量Y的熵的减少量反映由变量X提供的关于变量Y的附加信息,也称为互信息,其表达式为
IG(X,Y)=H(Y)-H(Y|X)
=H(X)-H(X|Y)
=H(X)+H(Y)-H(X,Y)
(20)
信息增益是一种对称性度量,即观察到X后获得关于Y的信息量等于观察到Y后获得关于X的信息量。对称性是变量与变量之间互相关的一个理想属性,但由式(20)计算得到的值更偏向于信息量更大的变量,而对称不确定性可以补偿偏向于信息量更大特征的信息增益偏差,并将其值规范化为[0,1]的范围。对称不确定性表达式为

(21)
在本文场景中,第i个需求响应特征fi熵的计算表达式为

(22)
式(22)中:Mi为特征fi的离散区间数量;Fu为特征fi处于第u个离散区间的样本个数;F为总的样本数。
电力用户类别c的熵的计算表达式为

(23)
式(23)中:Mc为电力用户类别总数;Fv为属于第v个类别的样本总数。
第i个特征fi与电力用户类别c之间的联合信息熵为

(24)
式(24)中:Fuv为特征fi处于第u个离散区间同时属于类别v的样本个数。
第i个特征fi与第j个特征fj之间的联合信息增益计算表达式为
(25)
式(25)中:Mj为特征fj的离散区间数量;Fuw为特征fi处于第u个离散区间同时特征fj处于第w个离散区间的样本个数;Fw为特征fj处于第w个离散区间的样本个数。
需求响应特征fi、fj之间和需求响应特征fi与用户类别c的对称不确定性为
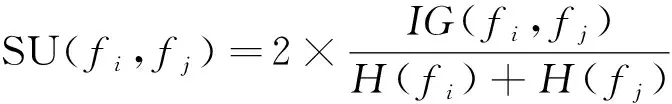
(26)
(27)
2.2 特征选择评价标准
假设共有c个用户类别、某个特征子集有k个需求响应特征,该特征子集评价值的计算表达式为
(28)

2.3 最佳优先搜索策略
在计算得到需求响应特征与电力用户类别的相关性和需求响应特征之间的相关性组成相关性矩阵后,使用最佳优先搜索策略生成待评价的特征子集。该策略步骤为:假设特征组合M开始于一个空的特征集,首先,将单个需求响应特征(假设共有N个)分别放入M中组成N种只含有一个需求响应特征的组合,分别计算这N种组合的评价值,并选择评价值最大的一个特征组合中的需求响应特征保留在M中;然后将已选需求响应特征和剩下的N-1个需求响应特征逐个组合成含有两个特征的组合,分别计算N-1种含有两个需求响应特征的评价值,挑选评价值最大且大于单个特征最优评价值对应的组合,并将该组合的两个需求响应特征保留在M中;以此类推即可寻得评价值最高的需求响应特征组合,即最优特征子集。为了节约计算开销、缩小搜索空间,特此设置一个停止搜索的附加条件:假设已选择i个需求响应特征加入M中,但连续增加三个特征所得到的各个最佳评价值都小于之前i个已选特征子集的评价值,则停止继续搜索生成新的特征子集,即认为已选的i个特征子集组合为最优特征子集。最佳优先搜索策略流程图如图2所示。
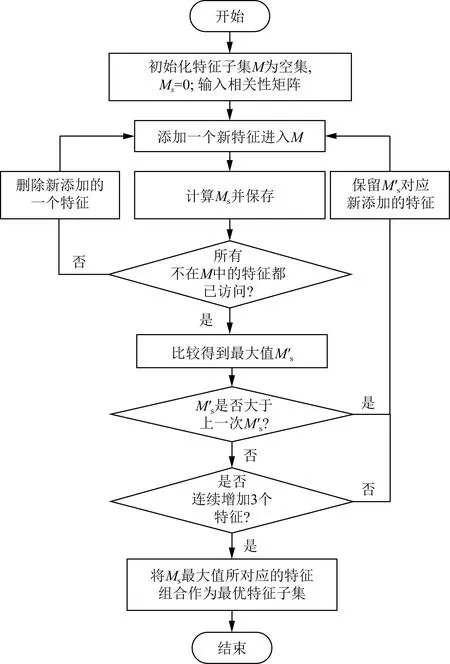
图2 最佳优先搜索策略流程图Fig.2 Flow chart of the best priority search strategy
3 算例分析
3.1 数据来源
以某市2015年某日实测310个典型电力用户的日负荷曲线为研究对象,数据细粒度为1 h/点,每条曲线共计24个功率点。经数据预处理后,本算例共有243条有效日负荷曲线。
3.2 聚类分析
以3.1节所述数据集为基础进行聚类分析,得到电力用户分类数、每一类的样本数量以及每一类用户用电曲线的形态特性,便于后续计算需求响应特征与用户类别相关性以及定义电力用户类别标签。
直接对已经过数据预处理的数据集进行聚类,采用K-means聚类算法[18],得到三类用户负荷曲线,如图3所示。

图3 三类用户负荷曲线Fig.3 Three types of user load curve
由图3可知,第一类用户在9:00—18:00持续高峰,其他时段用电水平较低;第二类用户在7:00—9:00和17:00—19:00出现两次高峰,整体用电水平较高;第三类用户在早、中、晚时段各出现小高峰、次高峰、最高峰,整体负荷水平呈上升趋势。因此,三类用户的类别标签依次分别为午晚长峰型用户、早高峰晚高峰型用户、早低峰午次峰晚最高峰型用户。
3.3 需求响应特征选择分析
为刻画电力用户互动潜力,定义了8个需求响应特征指标,以此构建原始特征集Tz={峰荷减少率、需求响应潜力熵、峰谷差率、负荷率变化比、峰时耗电率变化比、谷电系数变化比、峰期负荷率变化比、谷期负荷率变化比}。
因需求响应潜力熵值计算只与原始用电数据有关,只需要计算另外7个特征指标,为计算每一个样本点响应后的7个特征指标,首先利用用户响应度模型计算分时电价方式下各类用户响应程度以及需求变化量。原始电价为0.55 元/(kW·h),采用如表1所示的分时电价。
根据中国各地轻工企业需求响应的状况,可得该数据采集地区关于轻工业电力用户的电价弹性系数如表2所示。

表1 电力用户分时电价Table 1 Time-of-use electricity price for power users

表2 电价弹性系数Table 2 Electricity price elasticity coefficient
由于不同类别用户的用电特性和互动潜力存在差别,所以针对每一类用户需求弹性矩阵亦存在差别。采用2.1节方法分别求取每一类用户中每一个用户在分时电价作用下的电力需求改变量,由于篇幅限制,以文中第一类用户的典型负荷曲线为例,计算分时电价方式下每一时段响应后的需求电量变化量,如图4所示。
在求得每一个样本数据点对应的各个需求响应特征指标值后,依据3.1节、3.2节中的相关性计算方法,求得需求响应特征指标之间和需求响应特征指标与电力用户类别之间的对称不确定性,以此来衡量需求响应特征之间以及需求响应特征与电力用户类别的相关程度。其值介于0~1,值越大表明相关性越高,如表3所示。
由表3可知,当特征子集M中只有一个特征时,取特征p1,其评价值为0.147且最大;当M中只有两个特征时,取特征p1、p3,其评价值为0.189且最大;当M中只有三个特征时,取特征p1、p3、p5,其评价值为0.220且最大;当继续增加M中特征数时,特征子集的评价值都会小于0.220。由此可知,最优特征子集为M={p1、p3、p5},即最优特征集由峰荷减少率、需求响应熵、峰谷差率三个需求响应特征构成。

图4 第一类用户响应前后需求电量对比Fig.4 Comparison of power demand before and after the first type of user response

表3 特征与类别以及特征之间的相关性Table 3 Correlation between features and categories and features
可靠性是评价一个特征选择方法优劣的标准,为验证所选取的最优特征集的可靠性,本文以不同特征选择方法选取以文中数据为基础的最优需求响应特征子集,其次将各个方法得到的最优需求响应特征子集用于聚类,然后对比聚类的计算时间、聚类准确率。为便于比较不同特征选择算法的性能,在比较聚类结果时,应该对相同的数据集使用相同的聚类算法,本文中均采用K-means聚类算法。
由表4可知,无论在聚类时间还是在聚类准确率上,本文所提特征选择方法都显著优于其他两种对比方法,而且最优需求响应特征子集中需求响应特征的数量也是最少的,所以本文算法所选的最优需求响应特征子集在整体性能上优于其他方法。值得注意的是,原始特征集的聚类结果并没有优于经过特征提取之后的需求响应特征子集的聚类结果,这主要是由于原始特征集合包含太多冗余特征,冗余信息的存在对数据样本相似性度量带来了干扰,从而影响聚类质量。由此可知,从特征体系中提取有效性较高而冗余性较低的特征是必要的。

表4 不同特征选择方法性能对比Table 4 Performance comparison of different feature selection methods
3.4 电力用户互动潜力的画像分析
首先以电力用户日负荷曲线作为原始数据,经过聚类分析、用户响应模型分析将原始数据转化为需求响应特征值,然后通过本文所提特征选择办法得到最优需求响应特征子集,最后将最优需求响应特征子集中包含的需求响应特征对应的值归一化,采用雷达图对三类用户的互动潜力画像进行展示。类内行为画像分别如图5所示,类间标签画像对比如图6所示。
由图5可以清晰地表达各类用户的互动潜力,峰荷减少率反映用户响应前后峰值减少程度,其值越大表明削峰效果越明显;需求响应潜力熵反映用户用电曲线波动程度,其值越大表明用户互动潜力越大;峰谷差率反映用户响应前后峰谷差变化程度,其值越小表明移峰填谷效果越佳。
结合图5、图6分析对比可知,第一类用户需求响应潜力熵较大,峰荷减少率较大,峰谷差率较小,表明该类负荷具有较大的互动潜力,是参与互动的积极响应者,可科学合理地制定分时电价政策,进行移峰填谷;第二类用户需求响应潜力熵较小,峰荷减少率较小,峰谷差率较大,同时由图3可知,平均用电量偏高,整体用电比较规律,表明该类用户具有一定的互动潜力,是参与互动的普通响应者;第三类用户潜力熵较大,峰荷减少率偏大,峰谷差率较小,表明该类负荷也具有较大的互动潜力,是参与互动的积极响应者。

图5 三类用户互动潜力画像Fig.5 Portrait of user interaction potential of three types
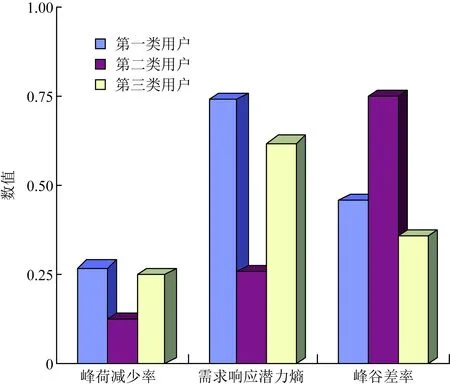
图6 类间特征对比Fig.6 Comparison of characteristics between classes
根据以上分析,对于积极响应者,可以给予政策优惠,支持此类用户参与调峰工作;对于普通响应者,可努力挖掘其互动潜力,降低整体用电水平,在用电高峰时段可以减轻电网负担。
4 结论
为建立考虑用户响应度的电力用户互动潜力画像,首先,在考虑分时电价作用下用户响应状态,建立用户响应模型,以反映用户响应程度;其次,定义反映用户响应度的需求响应特征体系,将原始数据转化为需求响应特征值;其次,为从反映用户响应度的特征体系中选择精简、可靠的特征指标,采用一种基于信息相关性的特征选择方法进行可靠的特征精简;最后,对已选择特征进行归一化处理,对其进行画像展示。算例分析表明本文所提方法不仅可以准确确定用户划分用户类别,制定用户类别标签,还能可靠、精简地选择最优特征子集,从而构建各类用户互动潜力的画像模型。所得计及用户响应度的电力负荷互动潜力画像可为电力企业挖掘用户需求与价值、进行用户细分实施精准营销提供有力支撑,同时有利于电网风险管控、把握规划方向。
