基于多粒子随机游走免疫算法
2022-07-09卢彬炜闫光辉
卢彬炜,闫光辉†,罗 浩,杨 波,张 磊,王 琼
1.兰州交通大学电子与信息工程学院,甘肃兰州 730070;
2.国网甘肃省电力公司信息通信公司,甘肃兰州730070
0 引言
传播广泛存在于自然界及人类社会活动中,分析复杂网络上的传播机理、设计高效免疫策略并有效调控网络传播是复杂网络研究与应用的经典问题,其中研究如何控制疾病与谣言传播爆发的免疫策略一直是网络传播的热点课题之一。鉴于免疫资源有限,无法免疫网络中所有节点,只能选择其中部分进行免疫,为此寻找一种高效的免疫策略具有重要的研究意义。
传统免疫方式包括随机免疫[1](random immunization,RI),目标免疫[2](targeted immunization,TI)以及熟人免疫[3](acquaintance immunization,AI),学者们所研究的方法多是以上经典策略的结合与改进[4~6]。研究表明,具有明显社团结构的网络中,免疫社团间的桥节点通常比免疫度值大的节点更能够有效地限制网络传播范围[7],而此类免疫方式的时间复杂度较高,为O(n3),需要较大的时间开销,且未综合考虑节点度值以及所处网络位置对网络传播的贡献能力,不适合在大规模网络中使用。
综上所述,传统或是改进研究多是将节点度值与节点位置信息分别考虑,且基于介数中心性的算法存在复杂度高等问题。因此,本文提出基于多粒子随机游走免疫算法用于无向无权网络免疫的研究,借鉴文献[8]随机游走免疫粒子在网络节点间游走免疫的思想,逆向考虑将节点间随机游走的粒子作为携带消息或是病毒的载体,获取一组对网络传播贡献大的节点,通过免疫此类节点进而控制网络传播。
1 本文算法
本文所做工作主要包含两部分内容:1)节点筛选工作,根据所提随机游走算法对网络进行多粒子游走,流量排序后按比例获取流量较大的节点;2)传播验证工作,根据游走所筛选的节点进行SI(suspected-infected)与SIR(suspected-infectedrecovered/removed)传播实验,通过与多种其他免疫方法对比,论证本文方法有效性与可行性。
本小节主要介绍多粒子随机游走免疫算法内容。
1.1 算法思想
本文假设网络中每个节点存在若干数目的粒子,仅考虑一个节点内的粒子(它可以是一条消息或是潜在的病毒,起源于网络传染源节点),粒子在连通的网络中随机游走。对于无向无权网络,网络中的连边代表节点间的联系,在传播游走的每一个迭代步中,粒子从当前节点移动至任一邻居节点,属于等概率事件。而在加权网络中,对连边的赋权可能代表了节点间的联系强度或是亲密程度,游走的依据需充分考虑节点间的联系程度或是亲密程度。因此,粒子游走概率亦受节点间连边权值影响,通过某一连边的概率为
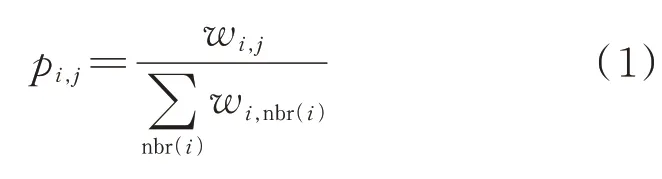
其中,wi,j表示节点i与节点j的连边权值,nbr(i)表示节点i的邻居节点。
基于以上描述,本文所选的无向无权网络可作为加权网络的一种特殊情况,即所有连边赋权为1。考虑到每一步的游走概率只与粒子所在节点度(加权网络中还需考虑边权大小)有关,并不会基于过去或当前的表现,且无法预知下一步的动态和方向,接近于布朗运动[9],根据其随机性命名为多粒子随机游走免疫算法(multi-particle random walk immunization,RWI)。
1.2 算法描述
定义1[10]对于网络G(V,E)(简记为G),令V=V(G)表示网络G的节点集合,E=E(G)表示网络G的连边集合。
本文若无特别说明,所使用的网络均为无向无权网络。
对于网络G(V,E),节点总数为n,单个节点生成的游走序列数为R。现仅考虑单粒子游走情况,设f(t)为该粒子在进行t步游走后的途经节点序列,即f(t)=[N1,N2,…,Nt],则实际游走步骤如下:
步骤1给定初始节点N0,即粒子所在初始节点;
步骤2设定最终游走迭代步数T,t为当前迭代步数,t=1;
步骤3遍历粒子所在节点的邻居节点,且当前节点度数为KNi,粒子随机游走至下一邻居节点Nt+1,概率为,令t=t+1;若当前节点无邻居节点,游走停止,流量记为0;
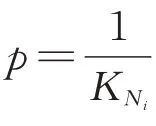
步骤4若t<T,进行步骤3;反之,游走结束;
步骤5流量统计:若序列中含有与该粒子起始节点相同的节点,移除;之后对所有序列节点数目累加求和,由高到低输出节点列表L(R,T)。
根据上述步骤,算法中完成单节点内单个随机粒子的游走共计使用了两次循环嵌套,粒子数目为R,游走生成的列表长度为T,且每个游走步骤需遍历当前节点的所有邻居节点与网络的平均度相关。在算法运行过程中,R、T和三类参数均与网络相关,设置为常数。设s为单节点内粒子数与游走深度及网络平均度的乘积,即

由以上描述可知s为常数。而网络节点规模为n,因此该算法时间复杂度为O(sn),数据存储的空间复杂度仅与网络节点数目相关,即为O(n)。
1.3 模型分析
根据游走规则,假定t时间步i节点的粒子数目为
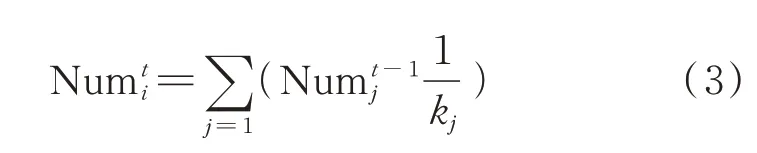
那么,经过T时间步后的游走,可得出节点i的途经粒子总数
事实上,(3)式作为对单节点某时刻的粒子数目的计算,可展开为如下转移式
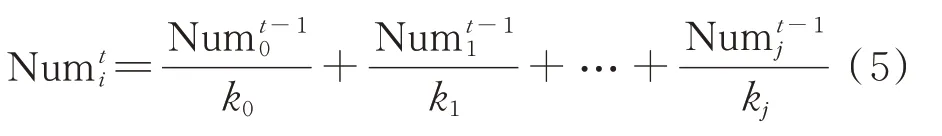
1.4 理论推导
以网络邻接矩阵表示网络中各节点的连边关系,对于无向加权网络可用0表示两节点间无邻边存在,用1表示两节点间存在邻边。那么,网络邻接矩阵可表示如下

节点间粒子的游走概率受节点的邻居数量影响,网络中每个节点的粒子迁入概率,其转移矩阵可表示如下

假设网络初始状态下每个节点中包含粒子初始数目均为R,根据上述游走算法描述,经过一步游走后的网络中粒子数量分布为
经过T步迭代游走后的粒子数量分布为
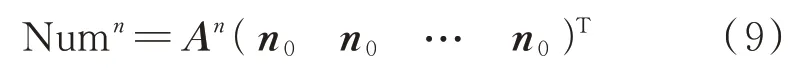
而本文算法考虑每一个节点的历史途经粒子流量,则需要把每一步的流量分布进行累加,即为(4)式。
P的计算与PageRank原理相似,是一种类马尔可夫过程,Google公司的PageRank算法[11]沿用随机游走思想,将游走的过程变为概率传播的过程,最后统计各节点的概率,但该算法最终会受网络出入度值的影响,形成某些无出度节点的“黑洞”,最终退化为节点度排序。本文所提的概率转移矩阵形式与PageRank算法的概率转移矩阵计算方式不同,PageRank表示在网络中的页面跳出关系,其统计的是最终的页面排序;而本文随机游走算法为统计粒子迁入概率,将每一个时间步的历史流量进行累加,考虑的是过程的流量。在游走过程中对每一步游走添加前提限制,考虑到现实传播受出度影响,因此算法步骤3对无出度或是无下一邻居节点做停止游走处理,流量记作0。
通过多个时间步的迭代,由(3)式可知,某个节点的粒子流量与两部分因素有关:一是受该节点度值影响,节点的度值越大,邻居节点越多,那么能得到邻居节点提供流量的机会越多;二是与该节点所处位置有关,如果该节点的邻居节点的度值不大,但该节点是桥节点,它也能获得较大的流量。由此推知当选取一定比例的节点进行免疫时,通过随机游走选取的节点集合中必然会有一部分与目标免疫相似,具体在实验部分详述。
2 实验与结果分析
2.1 数据集准备
为了验证本文算法的有效性,实验选取了真实网络共计8个不同数据集,包括不同尺度的具有无标度特性[12~15]与小世界特性[16~19]的网络。表1给出了这8个数据集的参数及描述。在本文中,以|V|表示网络中节点总数目,|E|表示网络中连边总数目,K表示网络节点平均度。
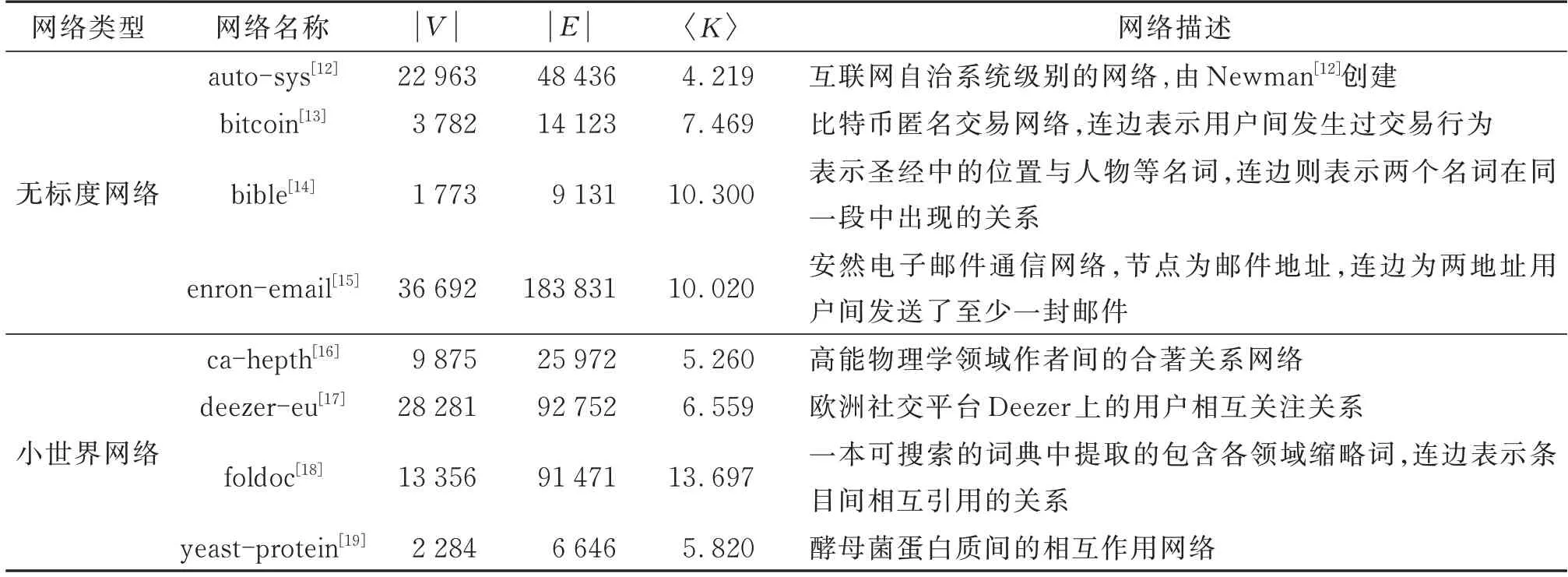
表1 数据集参数及相关描述Table 1 Datasets par ameters and r elated descr iption
2.2 实验设计
文献[20]的结果表明,疾病与谣言传播在无标度网络中的速度快且范围更广;在小世界特性的网络中,平均度越大,则传播峰值越高。由此根据不同的网络特征使用SIR与SI传播模型,本文主要选取五个已有的网络免疫策略进行横向对比来评估本文算法性能。
定义2在SIR与SI传播模型中,β表示易感节点与相邻感染节点接触后的感染概率,γ表示易感染节点的恢复概率,在SIR传播模型中,将有效传播率定义为λ,且λ=另外,λc定义为网络疾病暴发阈值,当λ>λc,传播现象将在网络中爆发并在一定时间步后达到峰值。
为了便于观察结果的差异性,在无标度网络中采用SI传播实验,而在小世界网络中采用SIR传播实验,并且SIR传播实验采用了不同的有效传播率。实验中对不同网络设置了不同的传播率β、恢复率γ和传播迭代步数。表2为实验参数设置。
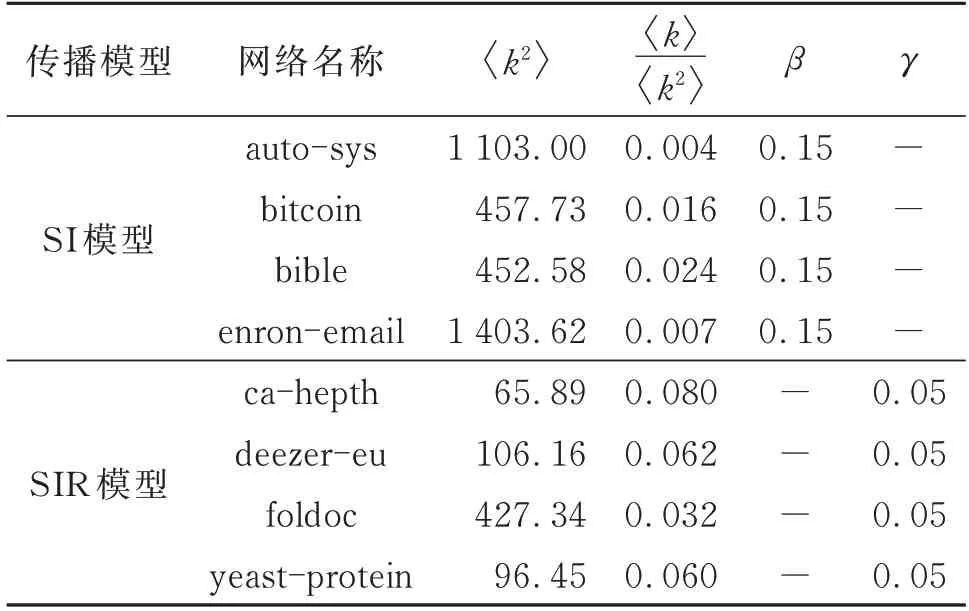
表2 传播实验参数设置Table 2 Spread experiments parameter settings
本文实验将恢复率定为0.05,使用的有效传播率区间λ⊆[0.5,4]。
不失一般性,本文实验次数设置为500次,网络中节点感染比例为每一次实验中最大感染率值的平均值。每次实验都选取固定比例(网络总节点数的5%)的节点作为网络传播的传染源,且传染源节点均随机生成,每次传播实验感染源节点都不同,能够保证在不同情况下传播爆发对网络采取免疫措施的有效性。
2.3 实验结果分析
与本文的RWI作比对的免疫策略有:熟人免疫(AI)[3]、目标免疫中的度中心(degree centrality)免疫TI_DC以及介数中心(betweenness centrality)免疫TI_BC[2]、PageRank筛选节点的免疫方式(PRI)以及文献[8]中的免疫粒子非独立随机游走免疫方法(dependent random walk particle immunization,DRWPI)。鉴于现实情况下免疫资源有限,且在实验准备过程中发现,在多数网络数据集中,当免疫率达到0.20时,网络传播范围已低于20%,甚至在有些情况下网络传播范围低于10%,控制传播效果明显,且已无明显的边际增益效果,因此本实验选取的免疫率均介于0.01至0.23之间,步长0.02。
图1给出了不同的免疫策略在无标度网络模型中的传播实验结果。多数网络中,当免疫率低于0.13时,RWI算法与TI_BC和TI_DC相比优势较小,当免疫率在0.13~0.23之间时,RWI算法要优于TI_BC和TI_DC。通过对感染率最大值的计算,RWI算法在4个无标度网络均优于目标免疫,显示出了更好的效果。
通过实验结果的对比,在具有无标度网络特性的数据集中,当免疫节点率较低时,RWI与目标免疫中的TI_DC和TI_BC的差异不明显,这是因为在低免疫率下,依据(3)式可以推测网络拓扑特征(即节点的度值)依然对网络免疫策略起决定作用,通过对比三种方法RWI、TI_DC和TI_BC的节点集,发现他们节点的重复程度很高,超过90%的节点是相同的,因此曲线几乎是重合的。而当免疫率较高时,三种方法在选取节点上体现了较大的差异性,说明此时随机游走能够辨识出更多易受传播影响的节点,此类节点在网络中虽没有较大的度值,但他们却处在易受影响的关键位置,比如连接不同社团的桥节点(这类节点往往度值较小,不易被目标免疫发现),亦或是在度相同的情况下,选取了更为重要的枢纽节点,这一类节点的邻居也许是度值较大,或是流量更大的节点。通过对这部分节点的免疫,能够更好地限制疾病向其他社团扩散并控制传播范围。可从图1发现,本文所借鉴的DRWPI方法在低免疫率条件下(免疫率低于0.20),控制传播的效果远不及目标免疫,这是由于DRWPI算法中的免疫粒子只能使节点具有暂态免疫效果,当粒子游走至其他节点时,当前节点将处于易感态,DRWPI方法仍不能有效控制网络的传播范围。
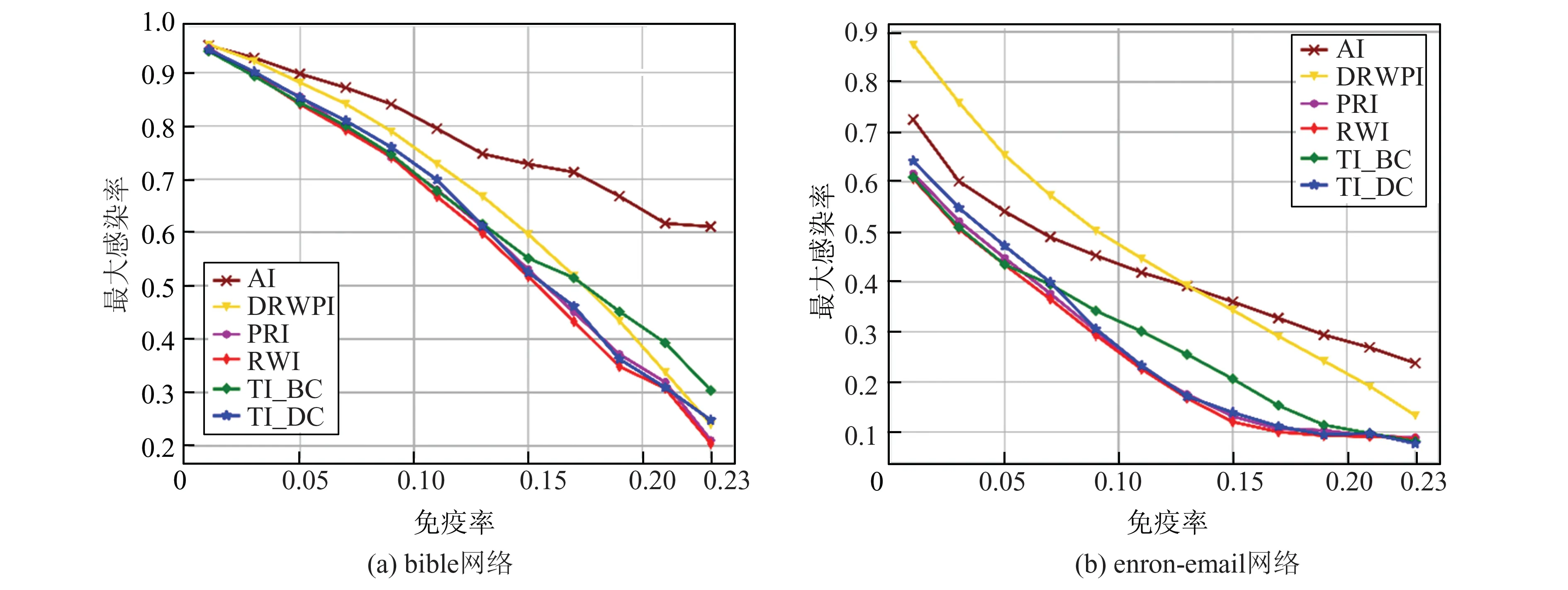
图1 两种不同无标度网络在不同免疫率下的传播实验Fig.1 Propagation experiment of two different scale-free networks in different immune rates
图2为当免疫率为0.11时不同有效传播率下的传播实验在具有小世界特性网络中的效果对比。与无标度网络相同,RWI算法均在控制网络传播的作用上比TI_BC和TI_DC有所提升。随着网络有效传播率的提升,传播范围逐步提升,从图2可以看出,DRWPI在较小的有效传播率下免疫的效果比其他免疫策略都要好,这是由于较低的有效传播率对节点的感染能力较弱,网络中移动的免疫粒子对传染有更好更快的控制能力。而随着传播率提升,网络中节点受感染概率增大,感染态(infected)节点数目会在极短的时间步内达到峰值,使得DRWPI方法中的免疫粒子无法快速响应并控制传播,DRWPI方法成了除AI之外最差的。从图2曲线走势也看出,随着传播率提升,RWI算法相比其他算法的优势更加明显。可见,RWI算法在高传播率下具有更好的免疫能力。
对比RWI和目标免疫选取的免疫节点集,二者识别出的节点排序有较大差异。从图1和图2可知小世界网络不同于无标度网络的度分布,小世界网络各节点的度值更加接近,由于差值较小,以度值为主要依据对节点的评价作用也随之降低;小世界网络具有较高的平均聚集系数,由于具有明显的社团聚集现象,因此会出现更多连接不同社团的桥节点和枢纽节点。通过分析网络的拓扑结构可知此类节点不易于发现,那么这种依赖于计算机算力的模拟仿真方式通过游走实验更容易筛选出网络中的易受影响节点。
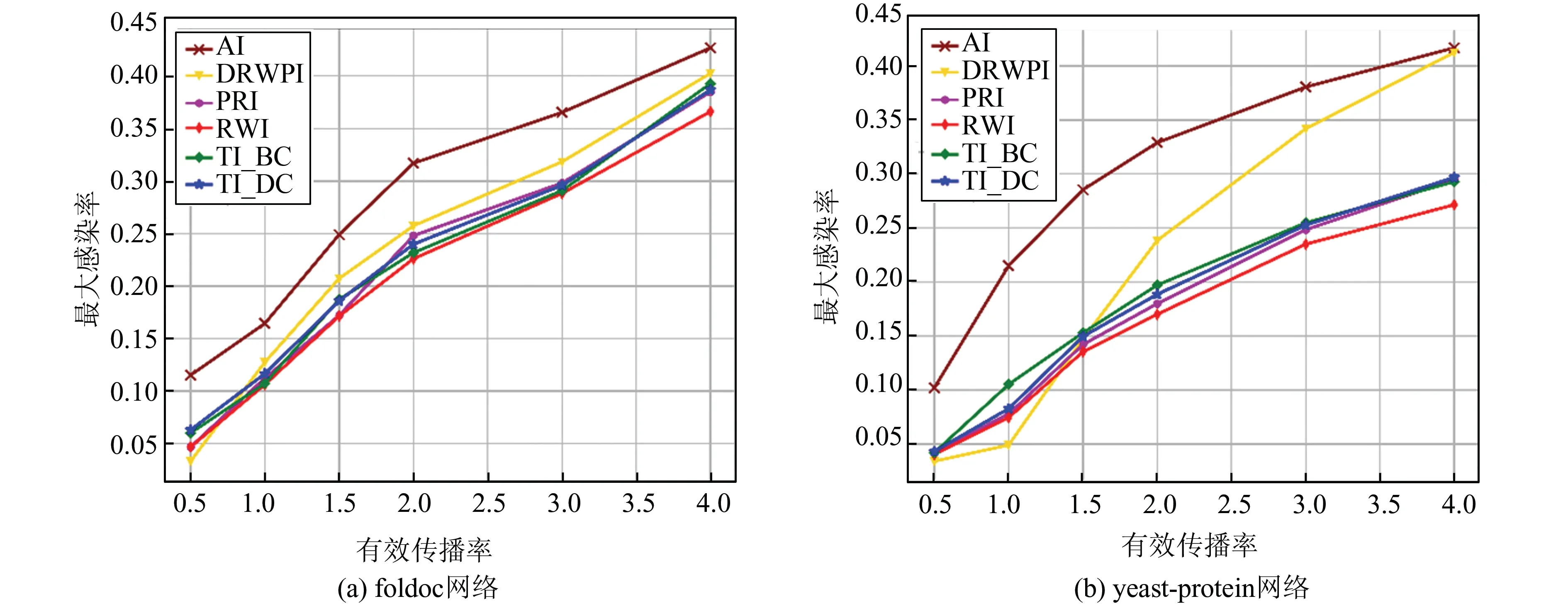
图2 在两种小世界网络中,当免疫率为0.11时,不同有效传播率下的传播实验Fig.2 Propagation experiment of two different small world networks with different effective transmission when immune rate was 0.11
图3为在有效传播率λ=3.0时,不同策略在enron-email网络与ca-hepth网络的传播比率。其中,免疫率分别为0.07和0.15。对比图2发现,RWI与目标免疫均能有效控制网络传播,不仅能够显著降低节点的感染数目,还能够有效减缓传播速度。相比而言,RWI则体现出更好的免疫效果。图3(a)和(b)是无标度网络下的SI传播,在传播一定时间步后,达到一个稳态,曲线越低说明最终传播范围越低,免疫效果越好。图3(a)和(b)中RWI的曲线是最低的,所以它的免疫效果是最好的。图3(c)和(d)是SIR传播,峰值越大说明传播范围越广,从中我们也可看出RWI的免疫效果较好。通过对网络选取适量的节点采取免疫措施尽管不可能完全阻止病毒或者谣言的暴发,但从图3中仍可知晓,免疫策略使传播速度减缓、传播范围缩小,对控制网络传播很重要。
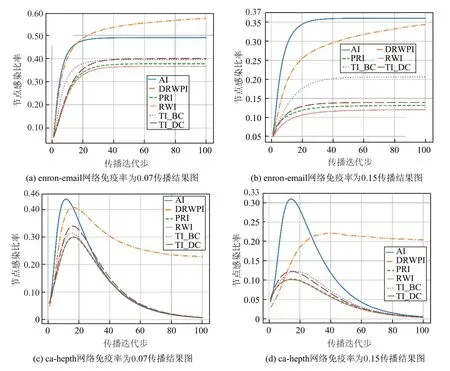
图3 真实网络中不同免疫率的传播结果Fig.3 The results of propagation experiment in different immune rates in real networks
上述两种不同特性的网络进行传播免疫实验结果对比表明,RWI算法在具有小世界特性的网络数据集中的免疫效果要显著优于无标度网络。这是由于无标度网络的结构所致,其网络度值更集中于少部分节点,度分布的差异性对随机游走算法的影响更明显,因此筛选出的节点与目标免疫方法的节点高度一致。而在小世界特性的网络中,它们分化出不同的社区,连接社区间的节点度值差异不明显,通过RWI在真实网络中更容易筛选出社区边缘节点与枢纽。正是由于在不同特性网络中的这种差异,使得RWI算法的有效性不会仅局限于理论,在实际应用中更加能体现其价值所在。
图4为RWI与TI_BC两种方法在不同数据集下运行时间对比。如前文所述,TI_BC的时间复杂度为O(n3),从图4可看出RWI的时间消耗占比明显更少;随着网络节点数量递增,两种方法运行时间的差异更加明显。从图4还可以看出,RWI相较于TI_BC在具有小世界网络特性的数据集中具有明显更低的时间占比,说明其对小世界网络特性的网络结构具有更好的适应性。
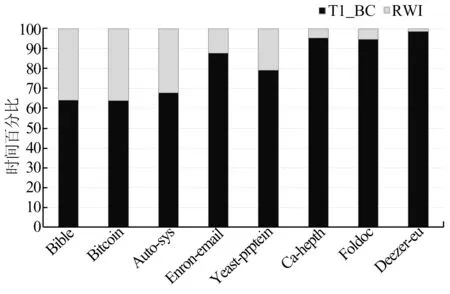
图4 RWI与TI_BC在不同网络运行时间百分比堆积图Fig.4 RWIand T I_BC in different network running time percentage stacking chart
3 结语
本文利用节点排序思想,通过结合多粒子随机游走的方式,识别关键传播路径上的节点,利用粒子累计游走数量作为节点的排序依据,通过对比多种经典免疫算法证实了RWI算法的有效性。
综合考虑节点度中心性以及位置信息对传播范围与传播爆发的时间影响,根据RWI算法在不同网络模型、不同传播模型进行实验的结果证实:
1)在无向无权网络中,由于真实网络的结构特性差异,对于社区化明显的网络,其社区边缘的节点对于网络传播具有重要作用,通过对网络中此类节点采取免疫能够有效抑制网络社区间的传播,说明RWI算法对控制现实传播具有指导意义;
2)由多粒子的随机游走实验结果可知,受传播机制与网络结构影响,节点的度中心性和所处网络位置存在一定差异,从侧面可以反映出节点传播能力并不只受节点度值的影响,在控制网络的传播问题时,也应充分考虑节点的位置信息,基于节点的随机游走算法对于找出此类节点具有更高的准确性;
3)相比于其他基于网络连边进行的随机游走算法以及基于介数中心性中节点对流量控制能力排序的算法,RWI具有更低的时间复杂度以及更广泛的使用范围。
综上可知,本文提出的RWI算法在不同类型不同大小的网络上均表现了较好的结果,在不同的真实数据集中,免疫资源有限的情况下,RWI被证明是优于现有的经典免疫策略。本文创新性地结合随机游走思想的免疫算法为后续的复杂网络传播控制提供了新的思路,针对多种不同的真实数据集传播实验,证明了算法在多种应用场景的有效性。
