垂荡式波浪能装置与风机平台集成系统水动力性能研究
2022-07-09朱良生周斌珍
高 琅,朱良生,王 磊,周斌珍
(华南理工大学土木与交通学院,广州510640)
1 前言
随着石化燃料日益消耗,可再生能源开发日渐紧迫,海上风机开发成为新的风能利用趋势。目前海上风机技术已相对成熟,波浪能装置也有丰富的研究与试验,但两者结合仍处于概念阶段。两者结合既可共享发电和系泊系统,降低经济成本,又可利用深海丰富的波浪能。因此,研究浮式风机平台与波浪能装置集成系统,在理论研究和工程应用上都具有较高的价值。
Peiffer等提出了将圆球型浮子加入WindFloat半潜式平台的概念,并通过试验验证数值模型,但未考虑粘性修正;波能浮子一般在共振周期附近工作,粘性作用不可忽略。Muliawan等提出了将垂荡式波浪能装置与SPAR平台相结合的概念,论述了集成系统可以增加经济效益。胡俭俭等通过数值方法研究了多个垂荡浮子与平台集成系统的总发电功率和平台受力。
目前集成系统的研究普遍将PTO阻尼理想化,处理成固定值或由给定参数控制的函数,未考虑使用最优PTO阻尼提高发电效率。
本文基于考虑粘性修正的势流理论软件AQWA,建立了阵列式垂荡波浪能浮子与浮式风机平台集成系统模型,研究其在规则波作用下的时域运动规律及波浪能装置发电功率,有望为实际工程中波浪能浮子设计与利用提供参考数据。
2 数学模型基本原理
2.1 运动方程
与单平台相比,垂荡式波浪能浮子加入浮式平台后平台受到的外力除波浪力与系泊力外,还包括粘性力和PTO阻尼力,其时域运动方程为:
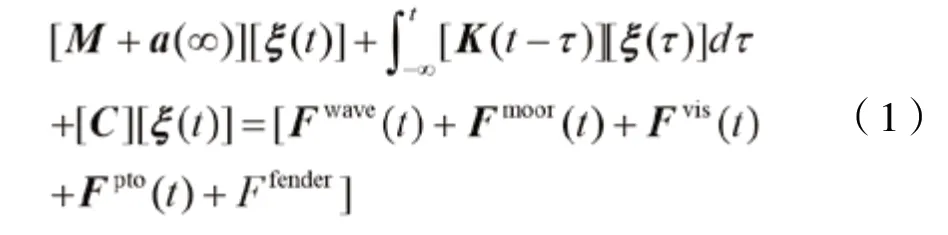
式中:为质量矩阵;为附加质量矩阵;、、分别为物体位移、速度和加速度;K(-)为迟滞函数;为恢复力矩阵;F为波浪力;F为系泊力;F为粘性作用力;F为PTO发电产生的阻尼力;F为浮子与平台间约束作用力。
浮子与平台运动方程相似,仅无系泊力。
2.2 浮子设计
本文基于无量纲方法设计的浮子尺寸,使其垂荡固有周期为给定海域周期。圆球底部形状浮子(图1),由圆柱与等直径半球底组成,圆柱水上部分固定为2 m,水下部分及半径r和总吃水d由下述推导确定。出于布置考虑,浮子中心需要直径= 1.7 m的开孔以设置约束。经数值分析,开孔对固有周期影响不明显。
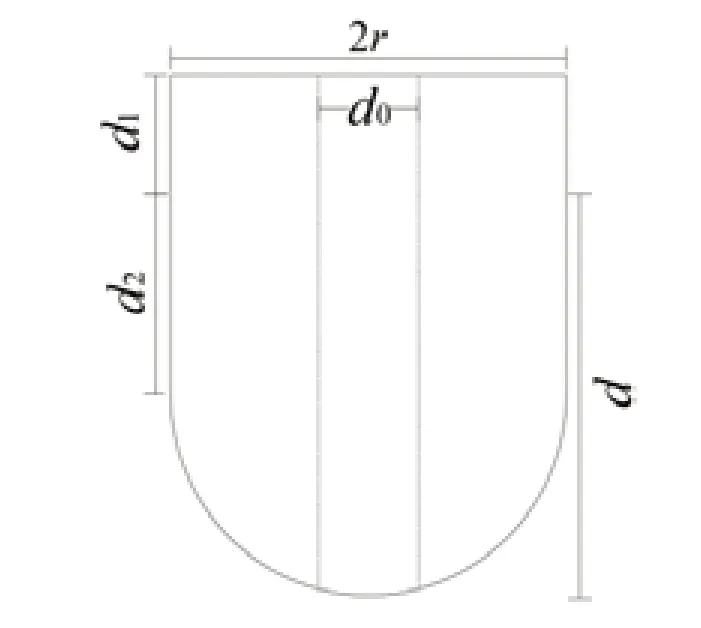
图1 浮子示意图
不考虑系泊下浮子垂荡方向的单自由度,运动共振周期为:
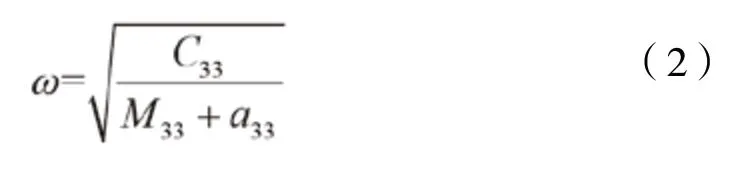
式中:为附加质量;恢复力与质量分别为
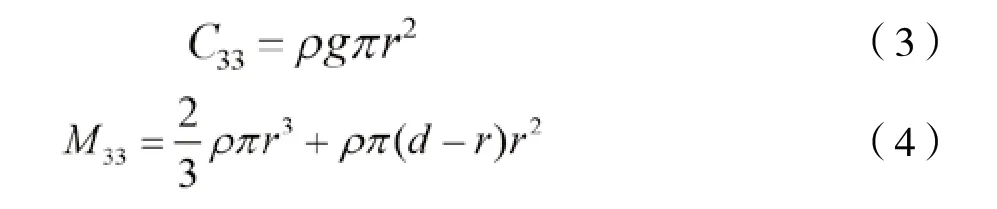
为海水密度;g为重力加速度。
不同尺寸浮子的附加质量与恢复力不同,可变换成显式迭代,引入无量纲参数:
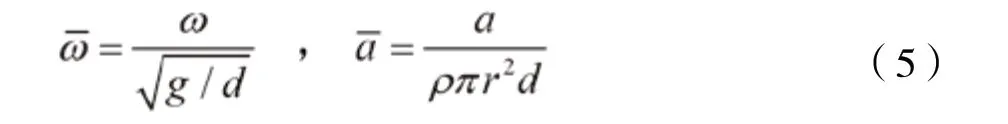
联立上述公式可得:

由此,可得到给定波浪周期与直径吃水比下浮子尺寸公式:首先赋予某一直径吃水比下的浮子初值,由软件获得该浮子附加质量,即可由公式(6)得出实际吃水与直径,两次迭代差值若小于1%即满足精度要求。
2.3 浮子最优PTO阻尼与粘性修正
考虑垂荡方向各周期下的最优阻尼系数:
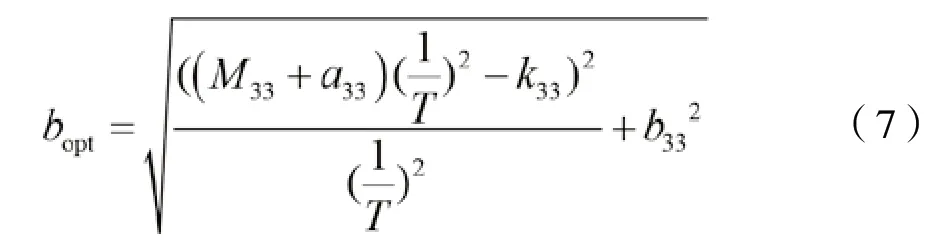
式中:为垂荡方向辐射阻尼;为垂荡方向刚度,取PTO刚度、系泊刚度和恢复力刚度之和。
平台在垂荡、纵摇、纵荡方向各添加8%临界阻尼考虑粘性影响:浮子垂荡方向受粘性影响较大,纵摇和纵荡方向由于受平台约束,自身粘性忽略不计。因此,仅对浮子垂荡方向使用自由衰减曲线法进行修正。
临界阻尼公式为:

式中:M为对应自由度共振周期处质量矩阵与附加质量之和;K为刚度矩阵。粘性修正值,见表1。
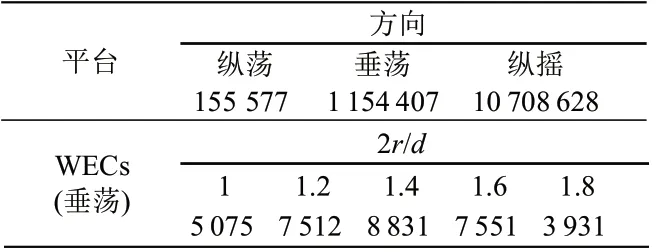
表1 平台与浮子粘性修正值N·m/(°/s)
3 数值模型
3.1 研究对象
本文以OC4风机平台(图2)为研究对象。该平台主体由三个浮筒、垂荡板和一个中心柱组成,横撑沿圆柱浮筒中心连线布置。
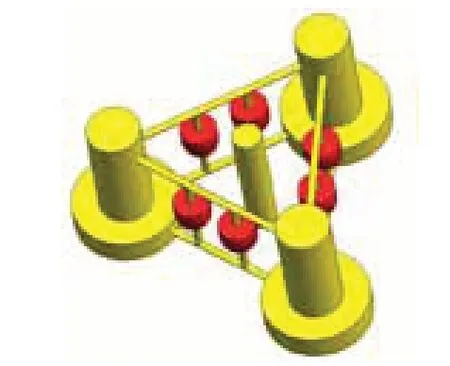
图2 平台示意图
3.2 浮子尺寸
以南海某海域的特征波周期T=5.3 s为目标周期,按照上述无量纲原则设计浮子主尺度,重心G设为水下部分型心,浮子布置如图3所示。浮子间距L=4,L=(L-4)/2,主要参数见表2。
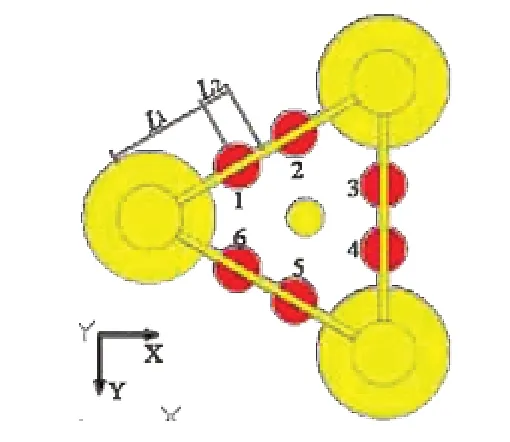
图3 浮子布置图
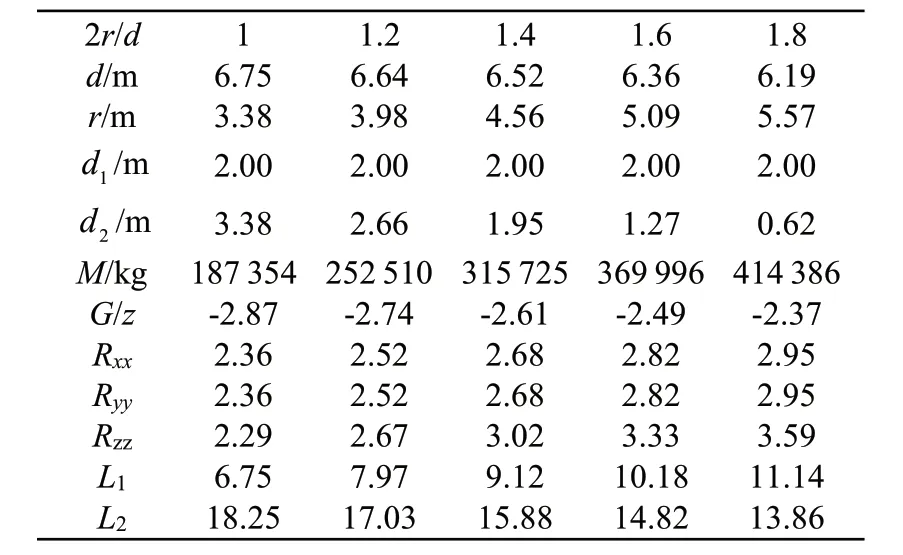
表2 浮子主尺度
3.3 水动力计算设置
水深设置为500 m,波浪沿X正向入射;利用AQWA的fender约束与用户自定义模块模拟PTO发电过程;在每个浮子与平台间隙沿X方向设置上下两对fender,强迫浮子在与平台纵荡和纵摇方向运动保持一致的同时,不影响其垂荡运动;Fender尺寸为0.05 m,受力方向为X方向,弹性系数A为10N/m,摩擦系数与阻尼系数设为0;浮子发电产生的阻尼力以函数F=B的形式定义,并编译成实时调用的dll文件来考虑PTO的阻尼力。
OC4采用三根悬链线系泊系统,系泊线夹角为120°,平台导缆点位于立柱上,导缆孔可活动范围为0.1 m、系泊布置和系缆参数见文献。
4 模型验证
4.1 数值方法验证
本文以Kelley给出的数据进行验证。考虑到Workbench AQWA在时域分析中积分到瞬时湿表面,WEC-Sim浮子的扁平形状使结果受波幅影响显著,设定波幅0.01 m,时间步长0.01 s、网格数13 248。
图4中浮子与平台相对运动的最大误差为3%,与Kelley结果吻合良好,验证了数值模型的准确性。
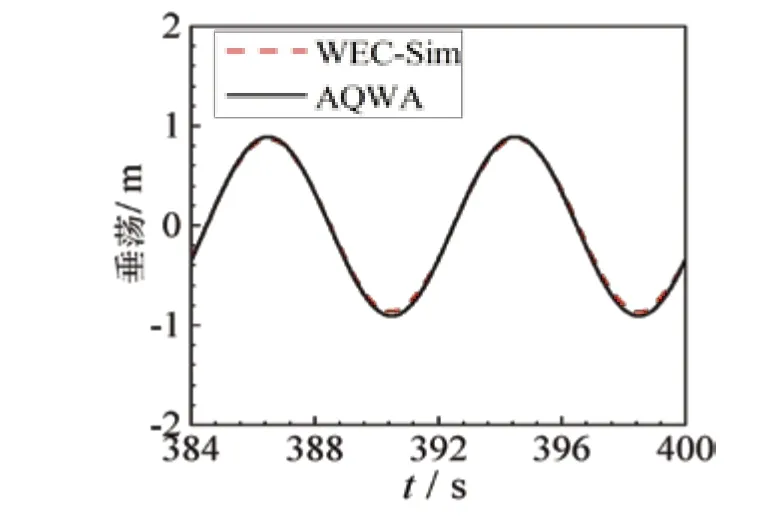
图4 浮子与平台相对垂荡运动对比
4.2 网格收敛性与时间步长无关性验证
使用Workbench AQWA中网格划分工具划分三种网格尺寸,验证水动力系数是否收敛;对于开孔结构,采用局部尺寸可以获得良好的网格。三种网格尺寸划分,见表3。

表3 网格尺寸划分
图5给出了浮子1垂荡方向附加质量,说明网格2已经收敛,其它方向及平台水动力系数结论相同。
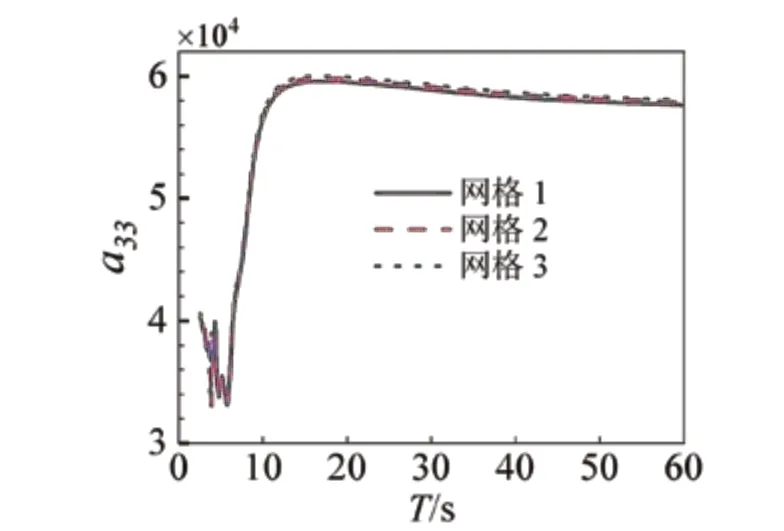
图5 不同网格下浮子1垂荡方向附加质量
选取网格2的尺寸进行时间步长无关性验证。入射波高H=0.2 m、波浪周期T=8 s、浮子与平台间阻尼B=2.54×10kN·s/m;
选择时间步长分别为0.005 、0.01 、0.02 s ,进行总时长为300 s的模拟计算。图6为三种时间步长下的纵摇时历曲线,t=0.01 s与t=0.005 s曲线的最大误差小于1%,本文选定0.01 s作为后续计算的时间步长。
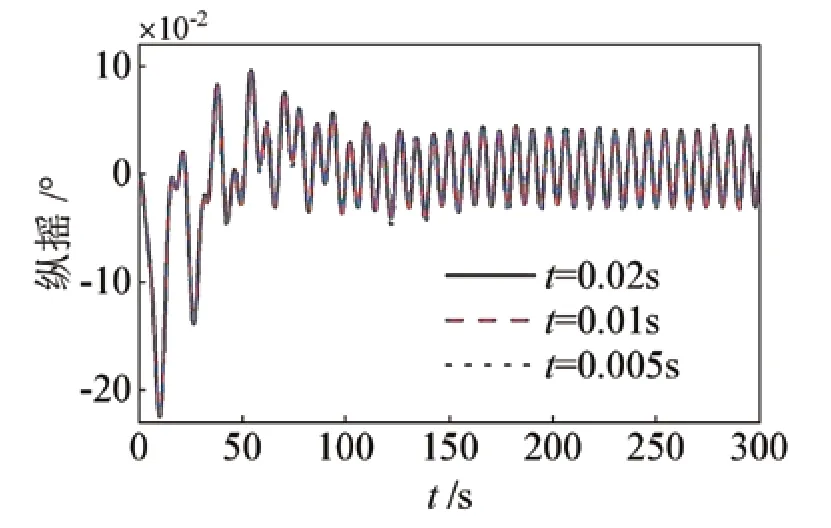
图6 不同时间步长下平台纵摇时历曲线
5 结果与讨论
5.1 浮子对平台运动响应影响
波浪能浮子的加入改变了平台周围的波浪场分布,并且因为PTO装置的相对运动而施加相互作用力。图7给出了单位波幅下,不同直径吃水比浮子加入后,平台的纵荡、垂荡和纵摇随波浪周期变化的运动幅值。
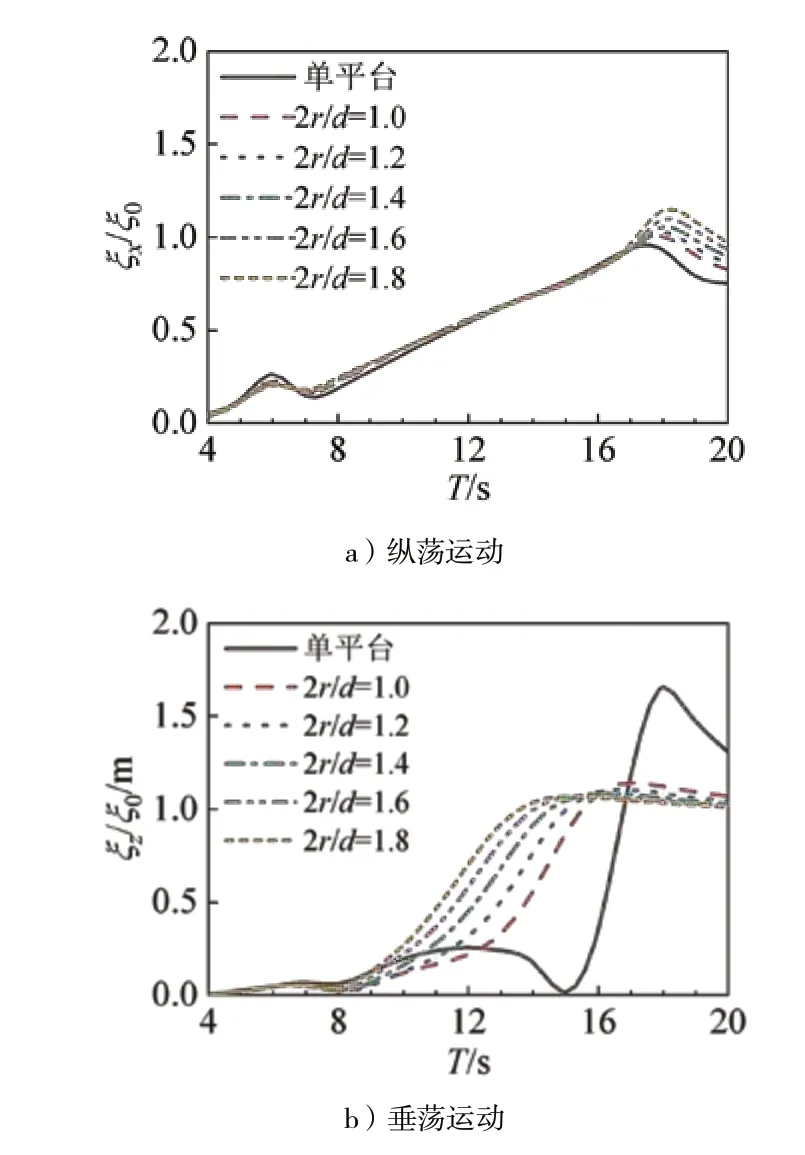
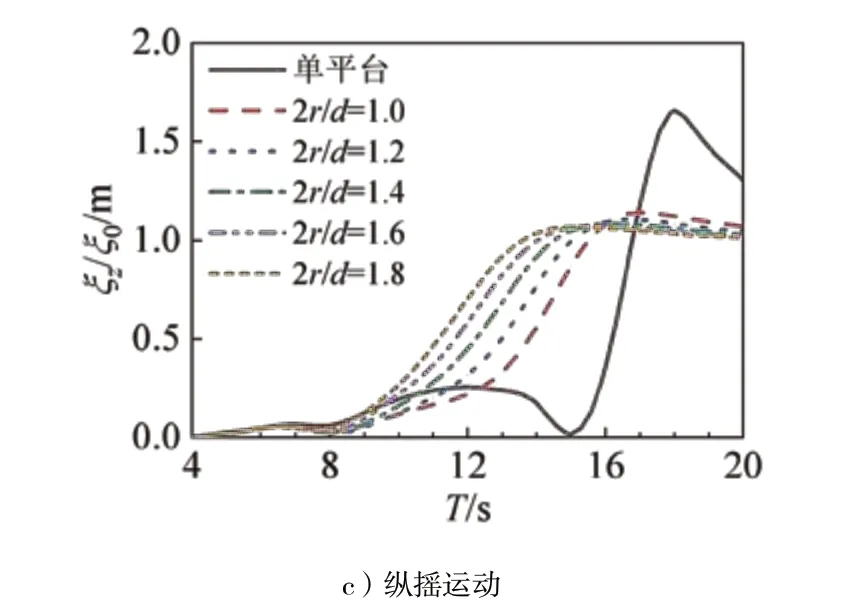
图7 平台各周期下三自由度运动幅值
由图7 a)可知,波浪能浮子对平台纵荡影响不大;对整个系统来说,浮子的加入增大了恢复力,相当于增加了平台纵荡固有周期(T=17 s),因此在T=18 s时运动峰值才达到最大。
由图7 b)、图7 c)可知,浮子对平台垂荡和纵荡的影响较为明显,且随直径吃水比的增大呈明显的规律性;浮子尺寸越大,对垂荡运动抑制越明显,但会增大纵摇运动。引起平台这两个方向运动变化的原因相同,为PTO装置施加的系统内力和内力矩;PTO阻尼随周期的增大而增大,平台所受波浪力在非共振周期处较小,共振周期处较大,PTO阻尼力表现为阻碍运动,因此在波浪力较小时增大运动、波浪力较大时减小运动。
5.2 浮子总发电功率规律
波能浮子一个周期T0内的发电功率为:

式中:V为浮子与平台的相对速度;P为浮子发电功率P之和:

图8给出了各尺寸发电功率随波浪周期变化结果,直径吃水比越大的浮子,总发电功率越大;不同浮子总发电功率变化趋势相同,先随波浪周期的增大而增大至峰值(此时T=7 s),随后逐渐降低;总发电功率峰值对应的周期,滞后于目标海况T=5.3 s,这是因为浮子发电功率由相对速度和PTO阻尼两个因素决定,在共振周期处浮子运动达到最大值,但PTO阻尼较小(图9),而后PTO阻尼随周期增大,对发电功率的贡献大于运动速度下降的影响,从而使得发电峰值对应周期大于海况周期。
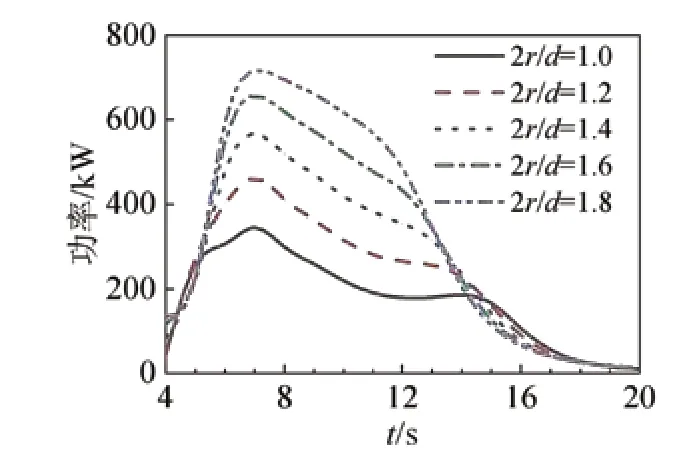
图8 浮子总发电功率
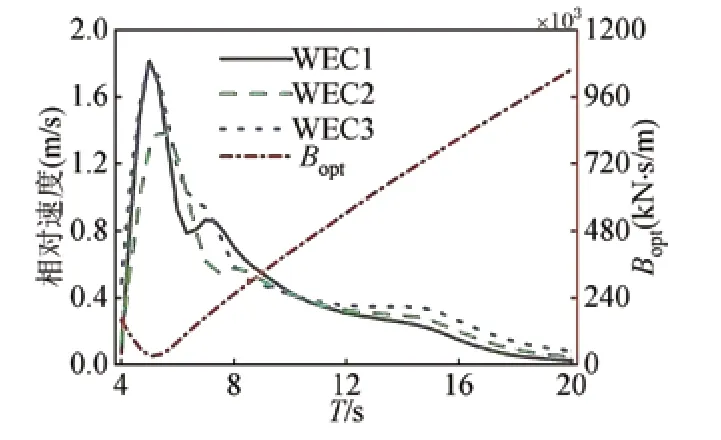
图9 浮子与平台垂荡相对速度与最优阻尼Bopt
集成系统每个浮子最优阻尼难以确定,本文按公式(7)计算,得到的各周期下单个浮子最优PTO阻尼并非实际最优阻尼。以直径吃水比2r/d=1.0的集成系统为研究对象,分析各波浪周期下等比例改变B值对浮子发电功率的影响。
由图10可知,实际最优阻尼略小于公式计算的单个浮子最优阻尼,根据周期的不同对应最佳值分布在0.75~0.8倍之间不等,发电峰值约提高10%。

图10 Bpto对发电功率的影响
5.3 Bpto对浮子发电量的影响
6 结论
本文针对垂荡式波浪能浮子阵列与浮式平台耦合运动及发电功率进行研究,得出以下结论:
(1)波浪能浮子的加入,可以降低平台的垂荡和纵摇峰值,但会增大非共振周期下的运动幅值;浮子对平台的纵荡影响不明显;
(2)浮子总发电功率峰值会滞后于运动峰值;
(3)波浪能浮子与浮式平台集成系统中浮子总发电峰值对应的最优PTO阻尼,低于单个浮子最优PTO阻尼,B为0.75~0.8倍B时,总发电功率最大。
本文研究结果,可为波浪能装置在浮式平台上的应用提供理论参考。
