基于密度峰值聚类并行麻雀搜索算法的食品机器人路径规划

郝 杰 唐叶剑

(1. 江苏旅游职业学院，江苏 扬州 225000；2. 安徽师范大学皖江学院，安徽 芜湖 241008)

随着食品工业化进程的不断加速推进，食品机器人在食品生产、加工等相关领域发挥的作用越来越大[1-2]，中国也相继在国家科技重大专项、国家髙技术研究发展计划等重大战略规划中提出了机器人研发课题[3]。移动机器人路径规划是当前机器人技术研究的热点之一，同时也涌现出了大量研究成果[4-6]，而机器人在食品分拣领域中的应用研究则相对较少。徐翔斌等[7]对移动机器人拣货系统进行了综合论述，并指出基于移动机器人的拣货系统能够大幅度提高物品拣选效率。刘芙等[8]以移动最短距离为评价指标，建立了食品拣取机器人双层路径规划模型，并采用改进的鸡群优化算法对模型进行求解，得到了总移动距离最优规划路径，但是该模型并未考虑路径的平滑度等因素，路径可行性需要进一步论证。张好剑等[9]以工位食品拣取顺序为优化目标，提出了一种基于遗传算法的并联机器人分拣路径优化方法，有效缩短了分拣行程，但是该算法需要充分考虑算法的运算速度以满足分拣实时性要求。余晓兰等[10]、赵相博等[11]、韦洪新等[12]则对食品拣取机器人涉及的视觉伺服控制、运动学基础和抓取臂空间建模等技术进行了论证研究，这些研究成果进一步推动了拣取机器人在食品领域中的实际应用。

研究拟对多点位食品拣取机器人移动路径规划问题进行探索，提出基于密度峰值聚类并行麻雀搜索算法的食品拣取机器人路径规划方法，并设计具有较高收敛精度和较快收敛速度的改进麻雀搜索算法[13-14]对模型进行求解，并通过仿真试验验证所提方法的可行性。

1 问题描述与模型建立

1.1 问题描述

在某食品生产企业仓库内，企业根据生产负荷、所需原材料种类、机器人装载量等因素，对仓库点位满载量、点位原材料放置种类利用RFID[15]进行信息识别优化，并将M个食品原材料存放点位划分为多个原材料拣取区域，每个区域包含N个点位，这N个点位存放的原材料能够满足生产一批食品所需物质，而且拣取机器人在一个工作周期内能够拣取完所有点位上的原材料。以单个原材料拣取区域为例，用序列(1,2,…,N)依次对N个点位进行标注，食品拣取机器人路径规划问题可以转化为：通过对机器人访问点位顺序以及点位间移动路径进行优化，使得拣取机器人在确保移动安全的同时，移动距离达到最优且移动路径更加平滑。

1.2 多点位路径规划模型建立

由于点位xi(i=1,…,N)的上、下、左、右4个方向都是潜在的机器人拣取位置，为了便于问题描述，取点位四周的中心位置为潜在拣取位置，并描述为xi,1、xi,2、xi,3和xi,4，显然拣取位置选取不同，点位间的移动路径也就不同，因此，食品拣取机器人路径规划问题不能简单认为是旅行商问题(TSP)[16]，其包含3层待优化问题：

(1) 访问点位顺序优化。机器人起始点xstar确定，当游历完所有点位后得到访问点位顺序集合X1(xstar,x1,…，xi,…,xN,xstar)，其中，xi为机器人访问的第i个点位的标号，显然访问点位顺序不同，得到的移动路径也就不同。

图1 潜在拣取位置确定示意图

(3) 点位间移动路径优化。设点位xi-1、xi的拣取位置为xi-1,a、xi,b，在xi-1,a与xi,b连线空间内找到n个点y1,…,yn，依次连接这些点得到点位间路径节点集合X3(xi-1,a,y1,…,yn,xi,b)，此时节点间路径距离di-1,i为：

(1)

定义xi-1,a与xi,b间路径平滑度φi-1,i：

(2)

φi-1,i值越小，表明路径越平滑。设机器人移动空间内存在m个障碍物，障碍物j最小安全距离为dsafe,j，则定义安全度S：

(3)

式中：

dj——机器人到障碍物j中心的距离，m。

对点位间移动路径优化的目的是在确保移动安全的同时，使得点位间路径更短和更加平滑。综上3层优化问题，建立基于总移动距离D(X1,X2,X3)、点位间路径平滑度φ(X1,X2,X3)和移动安全度S为评价指标的食品拣取机器人路径规划模型，目标优化函数为：

minf=S×[ω1D(X1,X2,X3)+ω2φ(X1,X2,X3)]，

(4)

(5)

0<ω1,ω2<1,ω1+ω1=1，

(6)

式中：

d(xstar,x1)、φ(xstar,x1)——起始点到第1个访问点位的路径距离(m)和路径平滑度(°)；

d(xN,xstar)、φ(xN,xstar)——最后1个访问点位到起始点的路径距离(m)和路径平滑度(°)。

从食品拣取机器人多点位路径规划目标优化函数可以看出，机器人拣取路径与点位访问顺序X1、点位拣取位置X2以及点位间路径节点集合X3息息相关，采用改进的麻雀搜索算法对模型进行求解，从而获取最优路径规划。

2 多点位路径规划模型求解

2.1 麻雀搜索算法

麻雀搜索算法(SSA)[17]是最近才被提出的一种新型群体智能优化算法，其通过模拟麻雀种群群体觅食行为，以实现对优化问题的求解。对于具有Q个体的麻雀种群，SSA算法根据麻雀个体目标函数值f(·)优劣，将麻雀分为发现者XDis、跟随者XFol和警戒者XVig，并赋予不同的更新进化机制(以最小优化问题为例)，t时刻(最大迭代次数设定为Tmax)有：

(7)

(8)

(9)

式中：

ξ∈(0,1)——均匀分布随机数；

q——服从正态分布的随机数；

L——单位向量；

R2——预警值；

ST——安全值；

A——由1、-1组成的向量；

β——控制系数；

ξ——极小常数。

SSA算法有一定的随机性和盲目性，SSA算法在迭代进化过程中，只选择种群最优解或者最差解进行学习，虽然加速了算法收敛速度，但是也导致算法种群多样性降低，容易陷入局部最优。为此设计密度峰值聚类优化麻雀搜索算法(DSSA)，利用改进的密度峰值聚类算法对麻雀种群进行聚类分析，根据聚类结果划分不同子族群，并重新定义麻雀迭代进化机制和编码方式。

2.2 DSSA种群聚类分析与迭代进化方式改进

密度峰值聚类算法(DPC)[18]认为，若数据点Xi的局部密度ρi高于附近点，且与具有更高局部密度数据点的距离δi较大，则Xi为可能的聚类中心，人为设定数据点截断距离dc，则ρi、δi计算公式为：

(10)

式中：

dij——Xi与附近数据点的距离，m。

定义聚类中心判定指标γi=ρiδi，DPC选取γi较大的点为聚类中心。从DPC实现过程可以看出，其参数设置简单，对数据具有良好的普适性[19]。由于DPC采用欧式距离进行数据点间距离度量，忽略了数据相关性对聚类结果的影响，因此采用协方差距离dD替代传统欧式距离度量：

(11)

(12)

采用改进的DPC(IDPC)对麻雀种群进行聚类分析，得到C个聚类，每个麻雀个体Xi被划分到某一分类中，用cXi进行描述(c∈[1,…,C]表示Xi所在分类)，此时同一类个体间具有更多的相似性，不同类个体具有更多的差异性，选取每个分类中目标函数最优的前K个个体组成发现者子族群，最差的U个个体组成警戒者子族群，其余个体为跟随者子族群。对3个子族群内个体按照目标函数值优劣进行排序，并重新定义进化机制。

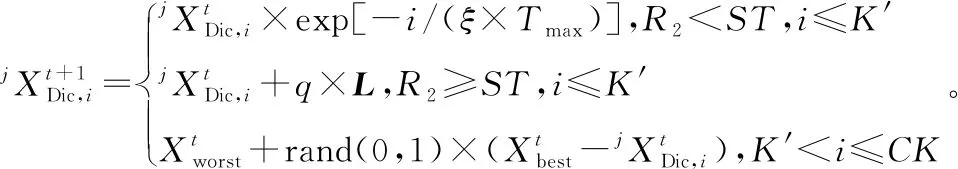
(13)

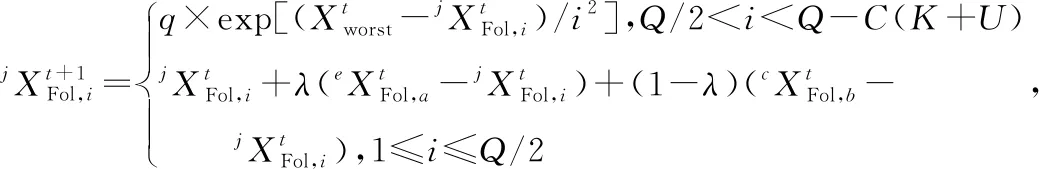
(14)

式中：

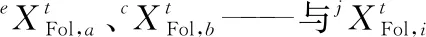
警戒者子族群内个体执行基本SSA警戒者更新操作。

2.3 DSSA求解多点位路径规划模型实现

(15)

式中：

(x1,…,xN)——机器人访问点位顺序集合；

(x1,a1,…,xi,ai,…,xN,ai)——点位拣取位置集合。

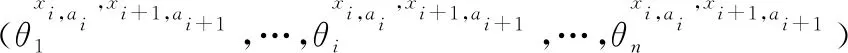
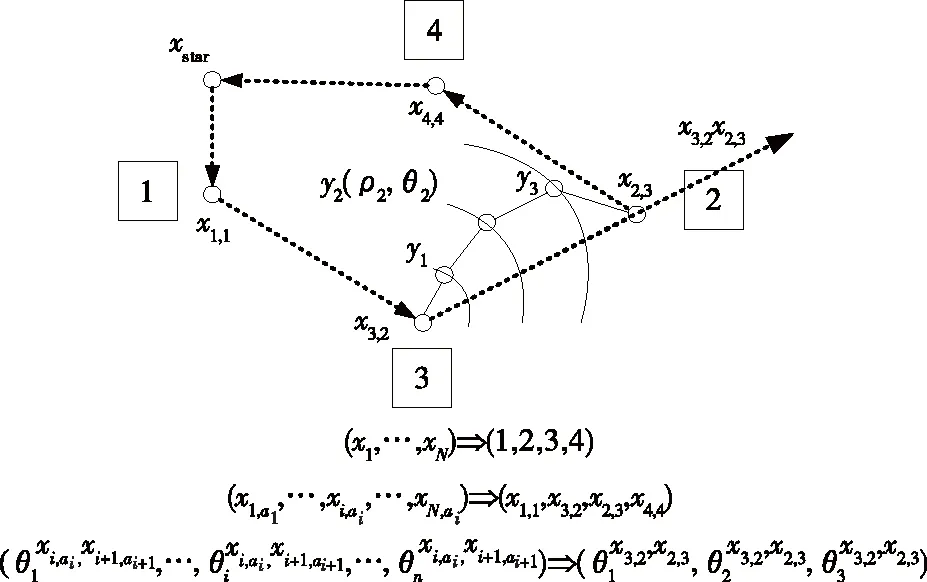
图2 麻雀编码含义示意图

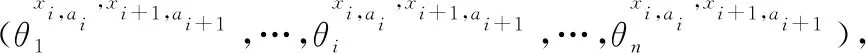
2.3.2 路径规划模型求解实现 对于食品拣取机器人多点位路径规划问题，采用改进的麻雀搜索算法进行求解，定义目标函数f(X)为：

(16)

(17)

麻雀种群根据编码定义式(15)，在解空间内随机产生Q个初始解，每个个体代表问题的一个解，即每个个体编码确定了机器人点位访问顺序、点位拣取位置以及点位间移动路径节点。在进化过程中，麻雀个体首先根据(x1,…,xN)、(x1,a1,…,xi,ai,…,xN,ai)信息，迭代进化求解出所有节点间当前最佳移动路径，然后更新种群信息，并对离散编码进行更新操作，如此反复最终实现最优解求解，从而得到食品拣取机器人移动路径。由于算法在每次迭代过程中都需要对Q个点位间路径以及从起始点出发到回归起始点路径进行优化求解，需要消耗大量运算时间，为此搭建MPI并行运算架构，每个线程执行一个节点间路径节点优化操作，以提升算法运算效率。图3给出了DSSA优化食品拣取机器人多点位路径规划问题实现流程图。

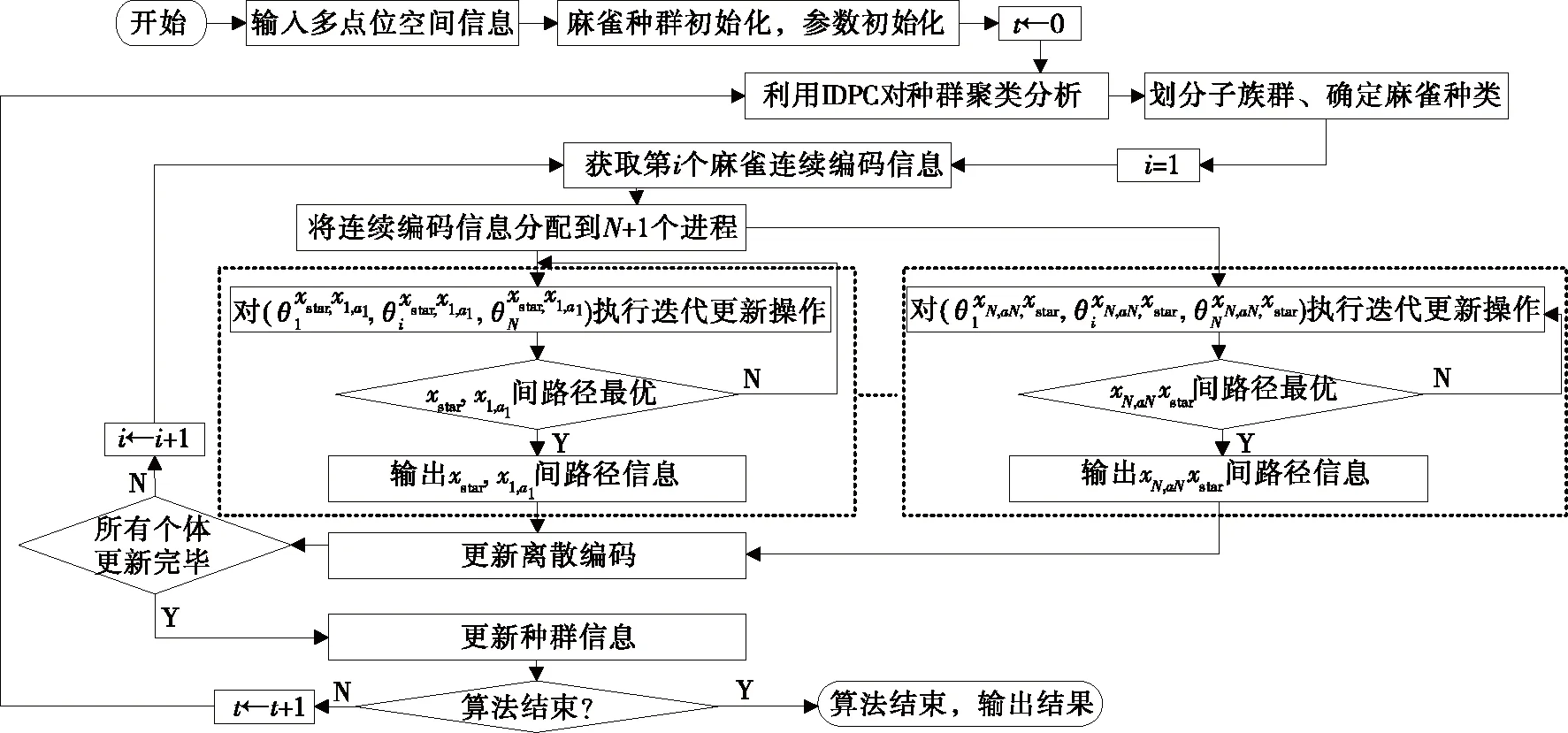
图3 DSSA优化食品拣取机器人多点位路径规划问题实现流程图

3 仿真试验与结果分析

3.1 DSSA性能验证

从图4、表1可以看出，在收敛精度上，对于函数f1、f3、f4和f5，DSSA都能以100%的成功率收敛于全局最优解，收敛精度明显好于其他3种算法；对于函数f3，DA、SSA算法的求解成功率只有91.6%和94.2%，低于其他2种算法；对于函数f4，DA、SSA算法的求解成功率更低，只有37.2%和40.1%，而SSA基本上找不到全局最优解；对于复杂病态函数f2，DSSA求解成功率达到了84.2%，而其他3种算法基本上无法实现全局最优解求解，表明DSSA具有更高的收敛精度。在算法运算时间上，由于DSSA在每次迭代过程中需要利用IDPC对种群进行聚类分析，增加了算法复杂度，因此DSSA算法需要消耗更多的运算时间。DSSA算法之所以具有较高的收敛精度，是因为在每次迭代过程中，都对种群多样性进行聚类分析，并根据聚类结果选取学习对象进行更新，从而使得算法具有较强的全局搜索能力，收敛精度更高。

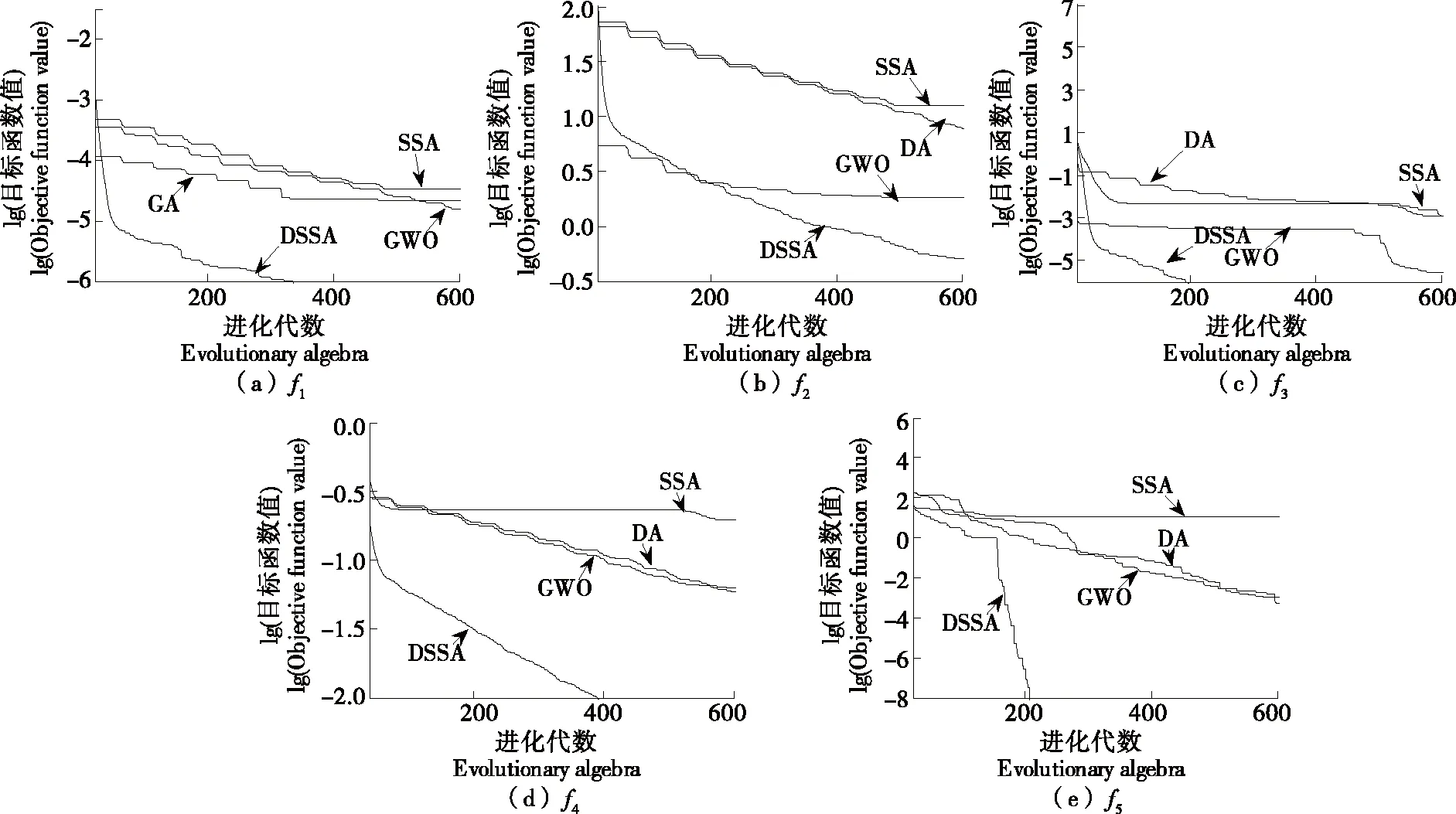
图4 4种算法函数收敛曲线

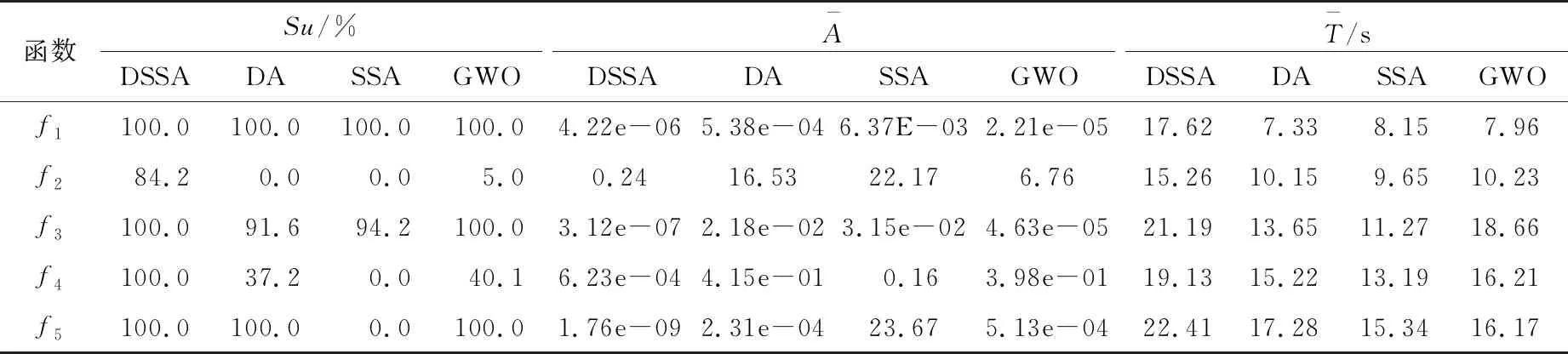
表1 不同评价指标对比结果

3.2 路径规划验证

3.2.1 实例仿真 某食品生产企业仓库为40 m×40 m的方形区域，该企业对食品原材料存放点位实行网格化管理，即将仓库划分为边长20 m的网格，因此共有16个点位，每个网格中心40 m×40 m的区域为食品原材料存放点位，距离每个点位边缘1 m中央处为潜在拣取位置，此外仓库共有9根半径为1 m的圆柱。某生产周期内，共有8个点位存放原材料，见图5(a)；移动机器人从(10,40)处出发，拣取8个点位存放的原材料，采用文中提出的路径规划方案进行求解，最终规划路径见图5(b)。表2 给出了规划结果。

从图5、表2可以看出，文中提出的基于密度峰值聚类并行麻雀搜索算法的食品机器人路径规划方法能够给出合理的路径规划方案，点位间移动路径曲线较为平滑，有效避开了圆立柱等障碍物，实现了对所有点位的有秩序访问。说明基于访问点位顺序、潜在拣取位置、点位间移动路径优化3层路径规划的模型，很好地反映了实际应用问题，而且采用DSSA对模型求解，能够找到合理的规划路径方案。

表2 食品拣取机器人路径规划结果

图5 食品拣取机器人路径规划图

3.2.2 对比试验 为进一步验证所提方法的性能，采用文献[8]提出的路径规划方法、GWO算法(GWO算法的编码方式以及并行计算架构参考DSSA)进行对比试验，仓库区域设定为100 m×100 m的方形区域，网格大小为20 m×20 m，每个网格的4个角放置半径为1 m的圆柱。随机模拟产生3种食品拣取应用场景：① 场景一，随机选取每列2个网格为放置原材料点位，共计10个待拣取点位；② 场景二，随机选取每列3个网格为放置原材料点位，共计15个待拣取点位；③ 场景三，随机选取每列4个网格为放置原材料点位，共计20个待拣取点位。每种算法独立运行10次，试验结果取均值，表3给出了对比结果。

从表3可以看出，对于4类应用场景，无论是移动路径总长度、平滑度还是移动时间，试验方法得到的优化结果都要优于其他2种算法，路径总长度缩短了约7.3%～39.2%，移动时间缩短了约26.7%～50.1%，而基于GWO算法得到的结果最差，表明试验方法得到的食品拣取机器人路径更优，这是因为：

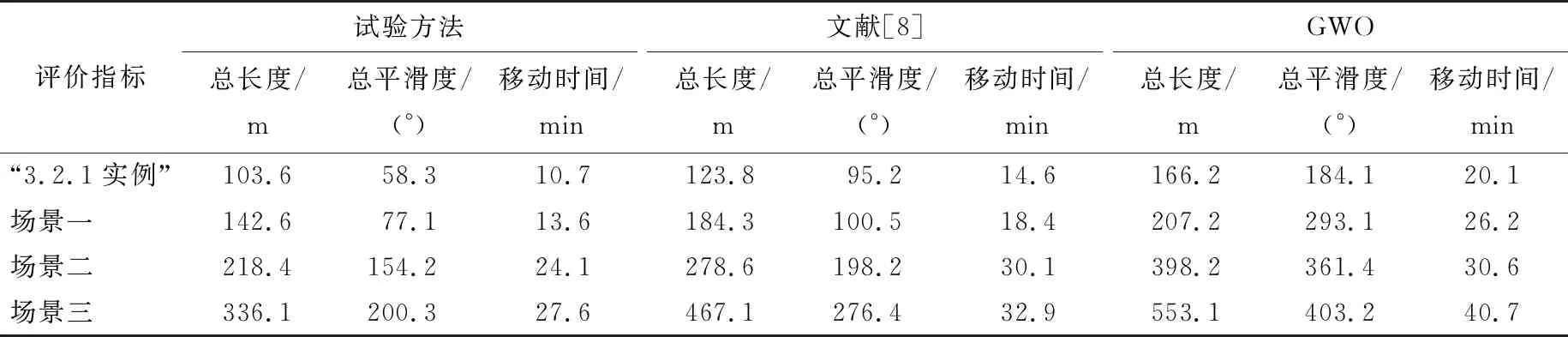
表3 不同方法路径规划结果对比

(1) 文中构建的规划模型更符合实际问题。文献[8]在路径规划过程中，先确定点位访问顺序，再依次确定两两点位间的移动路径，这种方法得到总移动路径不一定最优，而试验方法将3层优化问题统筹考虑，每次迭代过程中同时更新点位访问顺序、点位拣取位置和点位间移动路径，从而保证了在获取最优访问顺序的同时，节点间路径也是最优的。

(2) 文中提出的DSSA具有更优的全局寻优能力。采用IDPC对种群聚类分析，使得麻雀个体在选取进化对象时更有针对性，能够选择空间差异性更大的个体进行学习，保证了算法能够在更广的空间内进行搜索，提高了算法收敛精度。

(3) 文中设计的路径模型求解流程效率更高。针对基于3层优化问题建立的路径规划模型，重新设计了麻雀个体编码方式，并将MPI并行运行架构应用于求解过程，更符合模型优化流程，进一步改善了求解结果精度。

4 结束语

对多点位食品拣取机器人路径规划问题进行研究，提出了基于密度峰值聚类并行麻雀搜索算法的路径规划方法，建立了融合3层优化问题的路径规划模型，并采用改进的麻雀搜索算法进行求解，通过引入密度峰值聚类、改进个体更新机制、重新定义编码方式和搭建并行运行架构，使得获得规划路径总长度更短、更加平滑，具有一定的应用推广价值。