类比法和模型法在预测房地产开发建设项目水土流失量中的比较初探——以成都平原15个房地产建设项目为例

杨 易，张 雄

(四川水利职业技术学院水利工程系，四川 崇州，611231)

开发房地产是我国近年来推进城镇化建设的迫切要求，但房地产建设造成的水土流失业已成为城镇水土流失中不可忽视的重要组成部分。水土流失预测方法是否科学，预测量是否准确，不仅直接关系到水土保持措施的布设和水土保持投资的大小，还关系到能否为水土保持监测和水土保持工程验收提供科学合理的依据[1]，故其一直为水土保持方案编制的重难点。本文收集了15个成都平原房地产建设项目的基本资料，分别以类比分析法和数学模型法预测了其施工期的水土流失量，并对结果加以分析比较，以期为同类项目提供参考。

1 房地产开发建设项目水土流失量预测方法及特点

目前在生产建设项目中常用的水土流失量预测方法主要有：数学模型法、类比分析法、实地测试法、流失系数法、侵蚀倍率法[2]等。

数学模型法，蒋坤富等认为是一种完全经验性模型，实际应用中需要大量实验数据支撑，参数较难准确确定，还需要时间对实测数据进行修正[1]。

类比分析法是在邻近类似工程实测水土流失量数据的基础上确定预测项目的扰动后土壤侵蚀模数，故类比项目的选择及其实测数据的精度是影响预测精度的关键所在[1]。

实地测试法是最具说服力和最科学的方法，但房地产水土保持方案编制的周期一般较短，难以实现长时间的观测，再者，许多项目都没有真正开展水土保持监测工作[4]，因此，很难得到实测数据。

流失系数法一般用于弃土、弃渣流失量的预测，但其需要系统的调研和试验研究，且流失系数未考虑其位置与形态，取值任意性较大，常导致弃土、弃渣新增流失量的计算存在较大偏差[5]。

加速侵蚀倍率法为扰动后的土壤侵蚀模数与扰动前的土壤侵蚀模数的比值，徐永年认为该值与扰动前后地表相对裸露度、土体不稳定系数、土体相对密实度以及土地利用变化有关[2]，并提出了计算公式，但房地产项目几乎没有进行相关因子的测算，故可行性较低。

以往实际中房地产水土保持方案的编制多采用类比分析法进行预测，数学模型法由《生产建设项目土壤流失量测算导则》(SL773-2018)(以下简称《导则》)提出并加以推广，故本文拟采用这两种方法分别对成都平原15个房地产项目的水土流失量进行预测，并对结果进行比较和分析，以供方案编制人员参考。

2 水土流失量预测实例分析

城市房地产水土流失主要包括建筑拆迁及挖方产生的弃渣的堆弃、运输流失和因场地开挖造成的新增水土流失[3]。近年来成都市由于城市扩张，房地产改建项目较少，主要为新建项目，故水土流失以场地开挖所致的流失为主。为简化分析计算，本文仅计算比较施工期的新增水土流失量，且不计算永久弃渣的运输和堆弃流失量。

2.1 房地产开发建设项目概况

本文收集的15个房地产建设样本项目均位于成都平原，属中亚热带润湿季风气候区，具有春早、夏热、秋凉、冬暖的特点，年平均气温16.2℃，雨量充沛，日照较少，年平均降雨量在920mm左右，降雨多集中在6-9月，土壤类型主要以水稻土、紫色土为主。项目区属以水力侵蚀为主的西南紫色土区(按全国水土保持区划标准)，容许土壤流失量为500t/km2·a。15个房地产建设项目占地、建设周期、原地貌土壤侵蚀模数、降雨侵蚀力因子、扰动后土壤可蚀性因子等如表1所示。

2.2 水土流失量预测

2.2.1 类比分析法

根据《生产建设项目水土保持技术标准》(GB 50433-2018)，土壤流失量预测按照下式计算[6]：

式中：W——土壤流失量，t；

j——预测时段，1，2，即指施工期(含施工准备期)和自然恢复期两个时段；

i——预测单元，1，2，3，…，n-1，n；

Fji——第j个预测时段、第i预测单元的流失面积，km2；

Mji——第j个预测时段、第i预测单元的土壤侵蚀模数，t/km2·a；

Tji——第j个预测时段、第i预测单元的预测时段长，a。

本文根据每个样本工程的建设内容、施工工艺、施工时序、扰动方式和扰动强度、地面物质的组成，选择邻近在建或已建在水土流失强度、规律等实际情况相似的项目作为各个样本项目的类比工程。经走访调查，收集各个类比工程施工期间的水土流失监测数据，计算出其各防治分区扰动后的土壤侵蚀模数，并经修正得到样本工程占地各分区扰动后土壤侵蚀模数，其取值见表2。

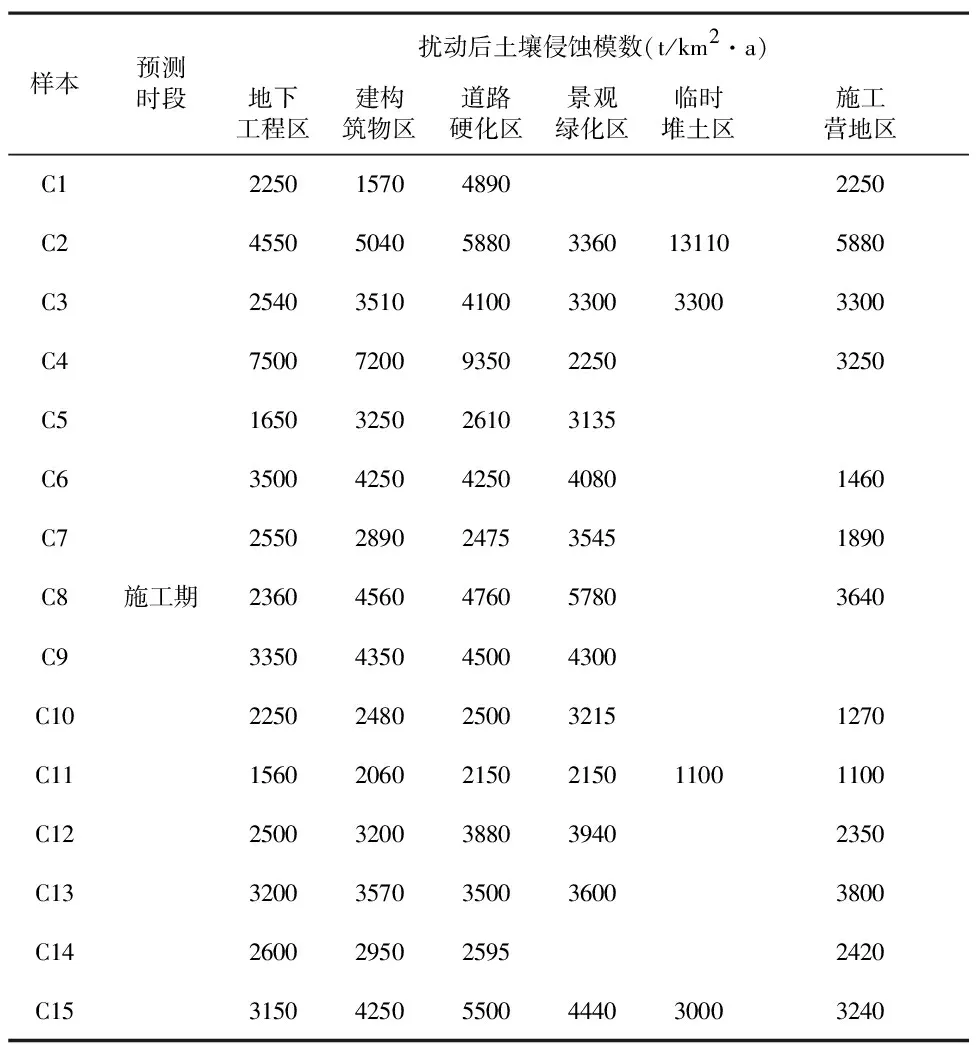
表2 15个房地产建设项目的水土流失防治分区扰动后土壤侵蚀模数统计

2.2.2 数学模型法

根据《导则》，扰动后的土壤侵蚀模数采用数学模型法确定，成都市所在区域生产建设项目主要为水力作用下的土壤侵蚀，该15个房地产开发建设样本项目各单元主要范围及扰动类型见表3。

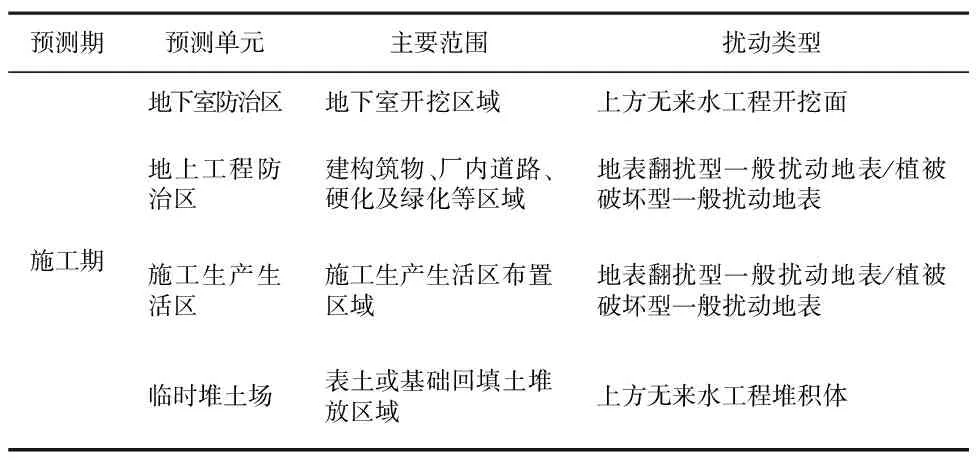
表3 土壤流失量预测单元扰动类型

扰动后各侵蚀单元的水土流失量计算如下[7]：

(1)上方无来水工程开挖面计算单元土壤流失量测算公式：

Mkw=RGkwLkwSkwA

式中：Mkw——上方无来水工程开挖面计算单元土壤流失量，t；

R——降雨侵蚀力因子，MJ·mm/(hm2·h)；

Gkw——上方无来水工程开挖面土质因子，t·hm2·h/(hm2·MJ)；

Lkw——上方无来水工程开挖面坡长因子；

Skw——上方无来水工程开挖面坡度因子；

A——计算单元的水平投影面积，hm2。

(2)地表翻扰型一般扰动地表计算单元土壤流失量测算公式：

Myd=RKydLySyBETA

Kyd=NK

式中：Myd——地表翻扰型一般扰动地表计算土壤流失量，t；

R——降雨侵蚀力因子，MJ·mm/(hm2·h)；

Kyd——地表翻扰后土壤可蚀性因子，t·hm2·h/(hm2·MJ·mm)；

N——地表翻扰后土壤可蚀性因子增大系数；

Ly——坡长因子；

Sy——为坡度因子；

B——植被覆盖因子；

E——工程措施因子；

T——耕作措施因子；

A——计算单元的水平投影面积，hm2。

(3)植被破坏型一般扰动地表计算单元土壤流失量测算公式：

Mkz=RKLySyBETA

式中：Mkz——植被破坏型一般扰动地表计算土壤流失量，t；

R——降雨侵蚀力因子，MJ·mm/(hm2·h)；

K——土壤可蚀性因子，t·hm2·h/(hm2·MJ·mm)；

Ly——坡长因子；

Sy——为坡度因子；

B——植被覆盖因子；

E——工程措施因子；

T——耕作措施因子；

A——计算单元的水平投影面积，hm2。

(4)上方无来水工程堆积体计算单元土壤流失量测算公式：

Mdw=XRGdwLdwSdwA

式中：Mdw——上方无来水工程堆积体计算单元土壤流失量，t；

X——工程堆积体形态因子；

R——降雨侵蚀力因子，MJ·mm/(hm2·h)；

Gdw——上方无来水工程堆积体土石质因子，t·hm2·h/(hm2·MJ·mm)；

Ldw——上方无来水工程堆积体坡长因子；

Sdw——上方无来水工程堆积体坡度因子；

A——计算单元的水平投影面积，hm2[8]。

由上，本文所述15个房地产开发建设样本项目降雨侵蚀力因子R和扰动后土壤可蚀性因子K取值见表1，地表翻扰后土壤可蚀性因子增大系数N取2.13，工程堆积体形态因子X一般取0.92，其余相关因子按测算导则计算或按实际情况选取[8]。

2.3 类比法和数学模型法比较

由以上数据，分别以类比分析法和数学模型法预测了上述15个房地产建设样本项目施工期的水土流失总量及新增水土流失量。结果见表4。

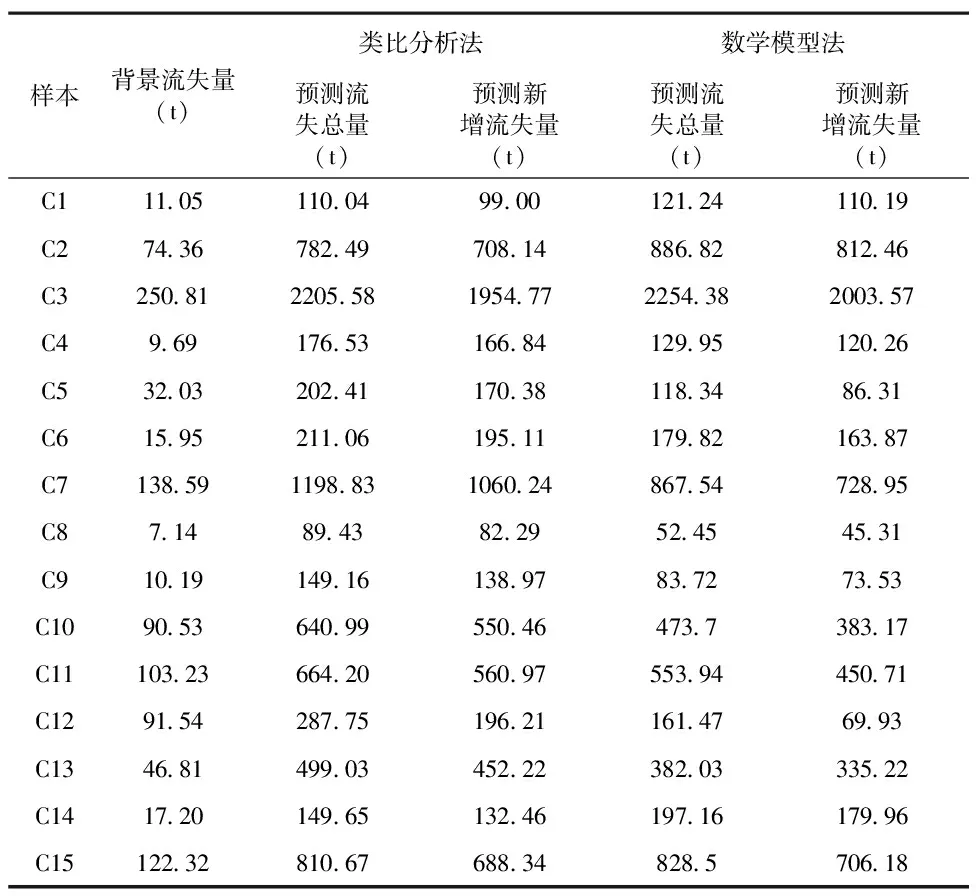
表4 类比分析法和数学模型法水土流失量预测结果

图1 类比分析法和数学模型法预测水土流失量对比

由计算结果和对比图可知，15个样本房地产建设项目中，仅5个项目通过数学模型法计算出的施工期水土流失量数据偏大，可知使用类比分析法时预测水土流失量会更多，结果倾向于更偏保守。

另由于：①每个样本的数据采集互不影响，符合使用方差分析的样本独立性前提；②水土流失是自然问题，符合使用方差分析的正态分布前提[9]，因此，可对各项目水土流失总量和新增流失量利用变差系数分析其离散程度：

计算可得：类比分析法水土流失总量Cv=1.037，新增流失量Cv=1.050；数学模型法水土流失总量Cv=1.178，新增流失量Cv=1.222。由此可见数学模型法计算的数值离散程度更大，笔者认为这是由于按测算导则计算或实际情况选取相关因子时，每一个项目的自身特点都能在其中得到一定程度的反映，更能体现不同项目的差异性，因此此方法比类比分析法所得出的数据更为准确。

3 结论

房地产建设项目的水土保持工作虽然开展了很多年，水土流失预测一直是这项工作中的重难点，一直没有很好的方法解决预测中的精度问题。以往实际中多采用类比分析法进行预测，但类比项目的选择及其实测水土流失量数据的精度都极易影响预测精度，编制人员计算时往往偏于保守。《导则》提出并推广使用数学模型法，但土质因子、坡度因子、坡长因子等相关因子涉及大量参数和较为复杂的计算，有较严格的适用条件且有赖于实验数据支撑，参数较难准确确定。笔者通过使用这两种方法对成都平原15个房地产建设项目的施工期水土流失量进行了预测，发现类比分析法预测的水土流失量往往更多，数学模型法更能反映各个项目内在的特点，数据更为准确。