达州市区洪水预测模型研究及应用

余世明，胡秀峰

(四川省达州市大型水利工程建设管理中心，四川 达州，635000)

2004年达州发生“9.3”特大洪灾后，达州市委领导高度重视，为了减轻洪水灾害造成的经济损失，时任市长亲自找国家防总有关专家建立了基于降雨量、洪峰流量、流域面积等为基本要素的达州洪水预测模型，并在2005年再次发生的“7.8”特大洪灾中对达州市区洪峰水位进行了科学预报，并提前通知灾区人民做好撤退防灾准备，减少了6.095亿元的经济损失[1]。可见，科学准确的洪水预报对防灾减灾工作是非常重要的。本文避开降雨量、洪峰流量、流域面积等因素，用洪峰水位资料，运用多元线性回归法[2]对达州市区水文站及上游宣汉县毛坝水文站、南坝水文站、黄金水文站2009-2018年实测洪峰水位资料进行分析，建立了达州市区洪峰水位一元、三元线性回归方程，作为达州市另一种洪水预报模型，以期能为达州市洪水预测预报提供更多的参考。本文重点对该模型的建立过程进行分析说明和验证。

1 基本原理推导

1.1 多元回归一般表达式

设多元回归一般表达式如下：

Y=a+b1X1+b2X2+……bnXn

(1)

设第i组实测值为Yi，有：

Yi=a+b1X1i+b2X2i+……bnXni+ei

(2)

式中：i=1，2……m为资料年数；ei为第i组理论值与实测值之间的差值。

则第i组实测值可表示为：

(3)

第i组估算值可表示为：

(4)

由(3)-(4)得：

(5)

1.2 推求回归方程中的a及bk值

要使实测值与估算值之间的平方和为最小，即：

(6)

从k中区分出j，其中k为横行脚标，j为纵列脚标。

1.3 建立多元线性回归方程组

利用bk·Skj=Sk0，当k=j=1，2……n时，利用k、j的任意组合，求出各Ski和Sk0之值，代入下列方程组：

(7)

求解以上方程组得各bk值，然后代入(6)式得a值，并将所求的a及bk值代入(1)式，便得多元线性回归方程式。

1.4 回归方程精度可靠性判断

判断回归方程是否可信，一般情况下，有复相关系数R，标准差△，相对误差振幅W等，其含义见表1。

表1 复相关系数、标准差、振幅公式及意义

2 洪峰水位线性回归方程建立

2.1 水文统计资料

达州市城区水文站及宣汉县毛坝水文站、南坝水文站、黄金水文站2009-2018年最大洪峰水位统计资料见表2。

表2 各水文站年最高洪峰水位时间～水位统计

2.2 建立线性回归方程

在统计表2中，达州市城区水文站与上游宣汉县境内的三个水文站洪峰水位发生时间跨度在2d以内的，认定为同一次洪峰水位发生时间。因此，达州城区水文站与宣汉县毛坝水文站、黄金水文站最大洪峰水位分别在2014年、2017年、2018年与2014年、2016年、2017年非同一次洪峰水位发生时间无相关关系，不能进行相关分析。

由于达州市区水文站与宣汉县毛坝水文站洪峰水位数据均以吴淞口海拔高程为准，而宣汉县南坝水文站、黄金水文站则以别的参照高程为准，这些水位高程不仅参照系不统一，而且与洪峰水位变化无关，在建模过程中将严重影响洪水预测模型的预测精度。为了减少对所建模型的精度影响，在建模前将各站统计资料减去同一水文站各年最高洪峰水位中的最小数据整数项，余数再建立线性回归方程。根据这一原则，各站减去洪峰水位高程分别为：达州市区水文站各年度最高洪峰水位减去270m、毛坝水文站各年度最高洪峰水位减去350m、南坝水文站各年度最高洪峰水位减去40m、黄金水文站各年度最高洪峰水位减去30m，整理后的水位数据见表3。

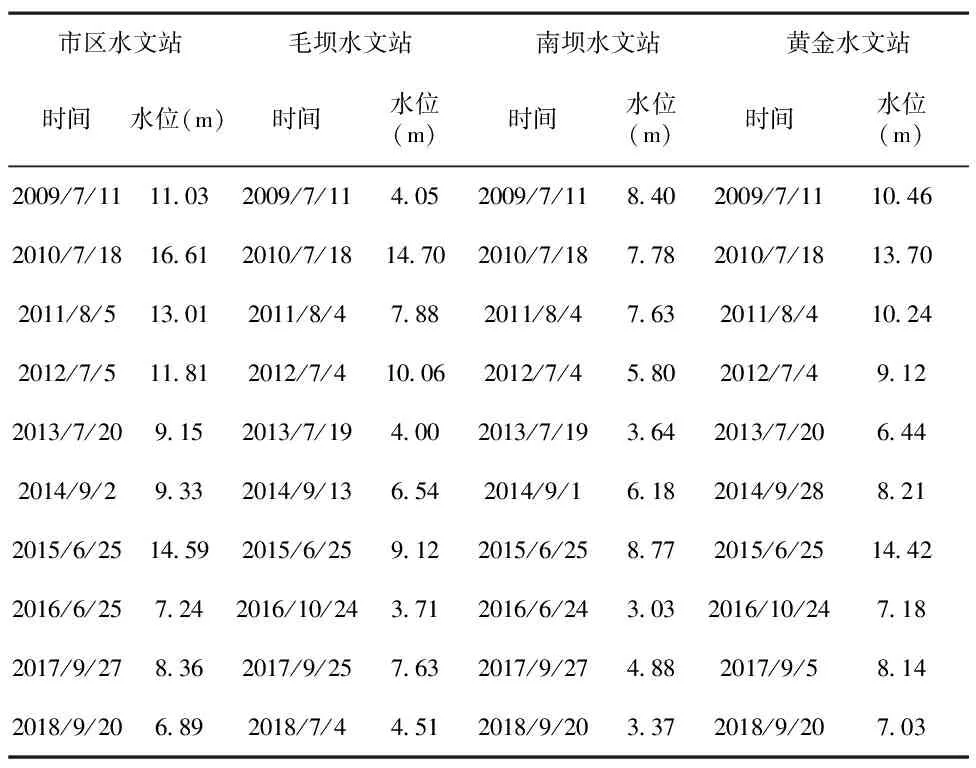
表3 各水文站最高洪峰水位数据整理

2.2.1 建立一元线性回归方程

设达州市区最高洪峰水位函数为Y1i、Y2i、Y3i，分别对应的宣汉县毛坝水文站最高洪峰水位H1i、南坝水文站最高洪峰水位H2i、黄金水文站最高洪峰水位H3i，根据回归方程原理，得达州市区水文站与宣汉县各对应水文站最高洪峰水位一元线性回归方程(见表4)。

表4 各站一元线性回归方程、相关系数、标准差、振幅

2.2.2 建立三元线性回归方程

由于线性回归方程预测精度随回归元递增而增高的规律，因此，在分析过程中未对上游三个水文站进行任意两站组合建立二元线性回归方程进行比较，而是直接将上游三个水文站最高洪峰水位有效数据同时纳入三元线性回归计算，建立三元线性回归方程。

从表2得知，在2014年、2016年、2017年、2018年，达州市区水文站最高洪峰水位发生时间与宣汉县三个水文站最高洪峰水位发生时间不是同一次洪峰水位发生时间，因此，建模时应将这4年的资料剔除。建立三元线性回归方程的有效数据见表5。

表5 四个水文站有效数据 单位：m

设达州市区水文站各年最高洪峰水位函数为Yi，宣汉县各水文站各年最高洪峰水位分别为毛坝站H1i、南坝站H2i、黄金站H3i，根据线性回归方程建模原理，利用表5数据，求得三元线性回归方程如下：

Yi=6.791+0.2663H1i+0.2146H2i+0.2047H3i

将宣汉县上游毛坝水文站、南坝水文站、黄金水文站各年最高洪峰水位资料代入上式三元线性回归方程计算、比较，检验结果见表6。

表6 三元线性回归方程预测值与实测值对比

经计算，复相关系数R=0.92；标准差Δ=7.3%。

从表6得知，三元线性回归方程预测值与实测值相对误差振幅W在-8.85%～8.6%之间，而一元线性回归方程预测值与实测值相对误差振幅W在-43.1%～21.1%之间，因此，在进行达州市城区洪峰水位预测时，利用三元线性回归方程进行计算。求得达州市区洪峰水位预测值后，再加上建模前减去的基数270m，得达州市城区洪峰水位(见表7)。

表7 实测值与预测值数据恢复 单位：m

2.2.3 成果验算

应用达州市水旱灾害防御中心提供的2021年8月29日洪峰水位(数据资料见表8)对建立三元线性回归方程进行验算。

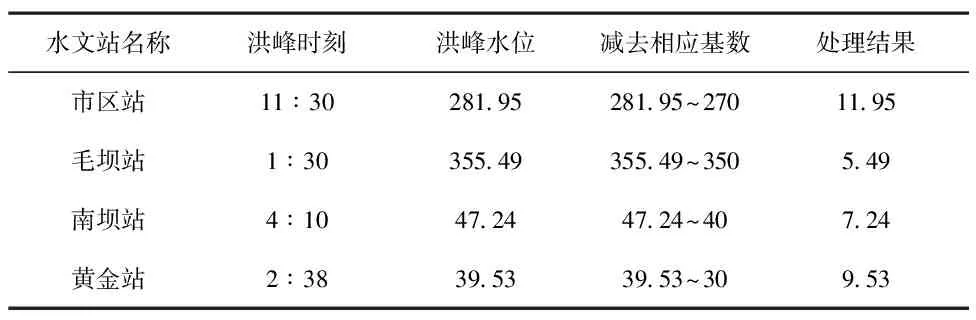
表8 2021年8月29日洪峰水位时刻及处理数据表 单位：m

将以上三个站处理后的数据带入三元线性回归预测模型验算：

Y=6.791+0.2663×5.49+0.2147×7.24+0.2047×9.53=11.7582(m)

所以，实际预测值为11.7582+270=281.7582(m)。

预测值与实测值绝对误差为：281.7582-281.95=-0.1918(m)。

数据处理后相对误差：-0.1918÷11.95=-1.61%；预测精度：98.39%。

数据恢复后相对误差：-0.1918÷281.95=-0.07%；预测精度：99.93%。

上游距达州市区最近的水文站为宣汉县南坝水文站，其洪峰水位发生时刻为4∶10，达州市区洪峰发生时刻为11∶30，两站相差7h20min。通过两站洪峰水位的时间差来通知灾区人民撤退搬迁，减少了经济损失。

3 结语

通过对达州市区水文站及宣汉县毛坝水文站、南坝水文站、黄金水文站洪峰水位资料进行线性回归分析，发现利用三个水文站的洪峰水位资料建立的三元线性回归方程理论值与实测值相对误差振幅W在-8.85%～8.6%之间，具有较高的可信度。应用2021年8月29日四个水文站洪峰水位数据进行验算，达州市区洪峰水位偏差19.18cm，数据处理后预测值与实测值相对误差-1.61%，精准度达98.39%；数据恢复后预测值与实测值相对误差-0.07%，预测精准度达99.93%。因此，运用三元线性回归方程，可以精准地预测达州市区洪峰水位，为达州城市防洪提供科学的决策依据。如果该方法在全国推广，每年可以减少上千亿元的经济损失，为国家作出积极贡献。

致谢：本文在研究过程中，达州市水旱灾害防御中心唐印主任、达州水文局高级工程师牟伦武科长提供了宝贵的实测洪峰水位资料，在此一并表示谢意。