Salp Swarm Algorithm for Solving Optimal Power Flow Problem with Thyristor-Controlled Series Capacitor

Balasubbareddy Mallala | Divyanshi Dwivedi

Abstract—In this paper, a salp swarm algorithm (SSA) is proposed for solving the optimal power flow (OPF)problem of a power system with the incorporation of the thyristor-controlled series capacitor (TCSC).The proposed methodology is implemented for determining the optimal setting of control variables for the OPF problem, which includes the real power of generators buses, voltages of generator buses, reactive power injected by shunt compensators, and tap changing transformer ratios.The performance of the proposed approach is validated and tested on the standard IEEE-30 bus system and single-objective functions, including transmission line losses.The severity factor has been minimized and the result obtained is compared with the existing algorithms.Simulation results achieved with the proposed SSA approach demonstrate that it results in an effective and better solution for the OPF problem.

1.lntroduction

The optimal power flow (OPF) is considered to be an imperative problem for energy management in power systems.In simple terms, OPF optimally adjusts the control variables of the power systems to optimize the objective functions, including the transmission line loss and severity factor, while considering both the equality and inequality constraints[1],[2].

In recent years, a number of classical and metaheuristic optimization algorithms have been developed by researchers to resolve the OPF problem.The conventional techniques used in [3] to [8] include quadratic programming, the Newton method, interior-point methods, gradient methods, and linear and nonlinear programming.However, as observed, these approaches cannot be implemented for large power systems and do not lead to global optimum solutions.Thus, the development of metaheuristic techniques has been undertaken by researchers to overcome the problems faced with the conventional techniques.These metaheuristic optimization techniques include the genetic algorithm (GA)[9], particle swarm optimization(PSO)[10], biogeography-based optimization (BBO)[11], gravitational search algorithm (GSA)[12], simulated annealing (SA)[13], Tabu search algorithm[14], and gray wolf optimizer[15], and are currently being implemented in power systems to resolve the OPF problem.

The current issues related to energy saving, energy utilization, environmental conditions, and increasing prices have created obstacles in constructing new generating units and transmission networks.So more efficient usage of the present transmission networks is demanded.This can be achieved by the incorporation of flexible alternating current transmission system (FACTS) devices, such as thyristor-controlled series capacitors (TCSCs) within the power systems.Detailed explanations of these devices were provided in [16] to[18]; in simple terms, FACTS devices readjust the power in the lines and bus voltages, and hence, enhance the usage of the present transmission networks.

In this paper, the salp swarm algorithm (SSA) proposed by Mirjaliliet al.[19]is employed to resolve the OPF problem in power systems by incorporating TCSCs.The standard IEEE-30 bus test system is adopted and the OPF problem is resolved in terms of different objectives, including the transmission line loss and severity factor minimization, under the consideration of constraints which include the power balances, real and reactive power generation, voltages, transmission lines, and physical limits of TCSCs.The optimal location of TCSCs is considered according to that recorded in the existing literature.The obtained results are compared with those of other metaheuristic algorithms to demonstrate the effectiveness and robustness of SSA in terms of resolving the OPF problem.

2.Steady-State Modeling of TCSC

In TCSCs, a controllable reactance is inserted in series with the considered transmission line.Fig.1shows a model of a transmission line with one TCSC placed between busmand busn.Under steadystate conditions, TCSC can be represented by a constant reactance, whereas in the power flow equations, the controllable reactanceis directly considered as a control variable.

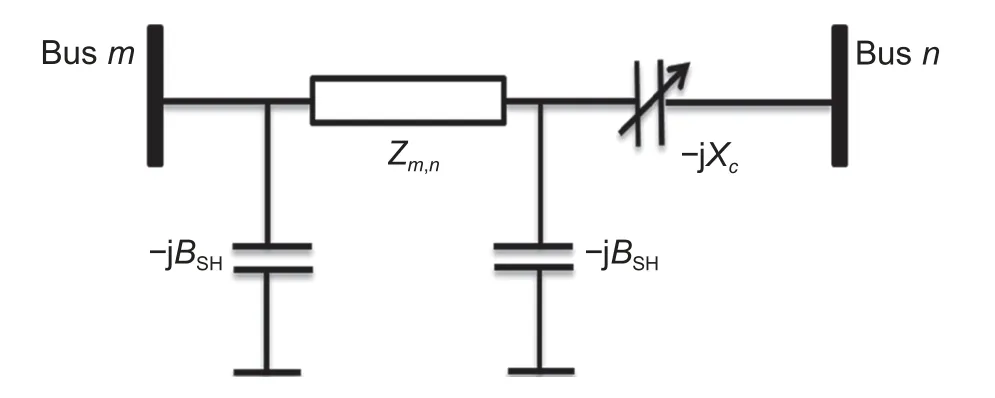
Fig.1.TCSC between bus m and bus n.

The modified real power (P) and reactive power (Q) flows from busmand busnare as follows:

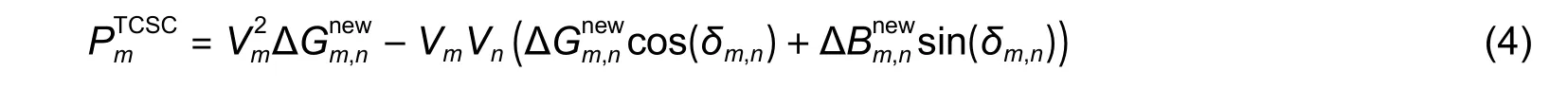
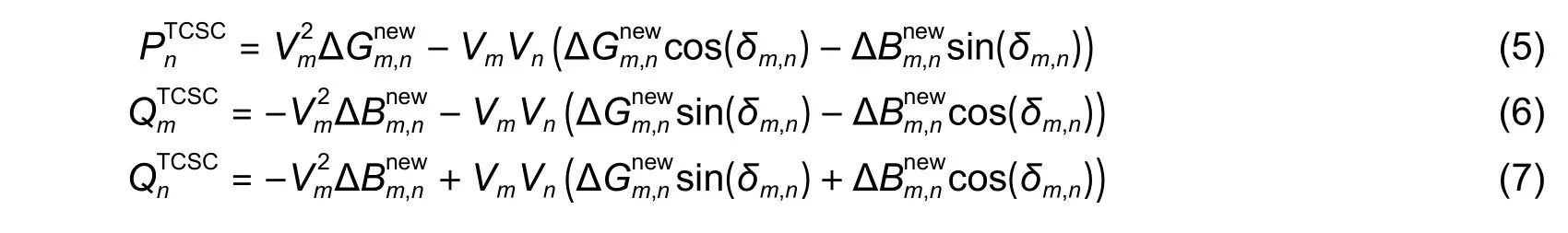
whereVmandVnare the voltages at busmand busn, respectively;δm,nis the phase angle between busmand busn;can be expressed as

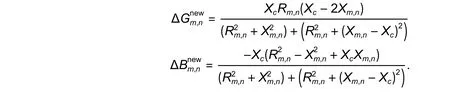
3.Problem Formulation

OPF helps in optimizing the steady-state performance of power systems in terms of specific objective functions with the equality, inequality, and device constraints.Mathematically, the OPF problem can be expressed as follows:

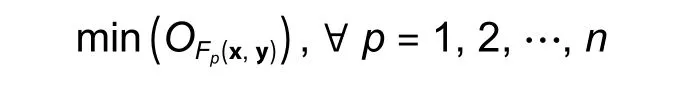
subject to

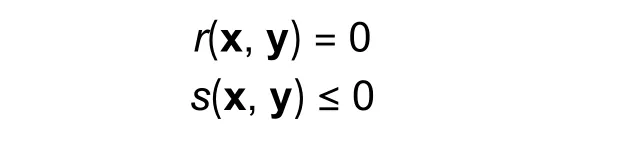
whereFp(x,y) is the various optimal power flow functions, such as the transmission line loss and severity factor;randsare the equality and inequality constraints, respectively;xandyare the vectors of the dependent and control variables of the system, respectively;nis the total number of objective functions.

The state vector can be represented as follows:

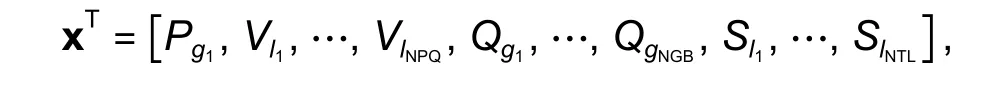
meanwhile, the control vector can be represented by

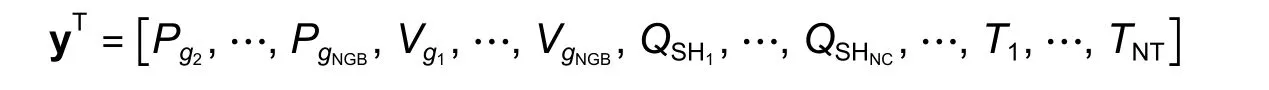
wherePg1is the real power of generator 1,Pg2is the real power of bus 2,Vl1is the voltage of load bus 1,Vg1is the generator voltage of the slack bus,Qg1is the reactive power of generator 1,QSH1is the reactive power generated by shunt capacitor 1,Sl1is the apparent power of generator 1, andT1is the tapping setting of transformer.And NPQ is the number of load buses, NGB is the number of generator bus, NTL is the number of transmission lines, NC is the number of shunt compensators, and NT is the number of off-nominal tap transformers.

3.1.Objective Functions

In this paper, two single objective functions are minimized, which are mathematically expressed below:

i) Minimization of the transmission line loss.

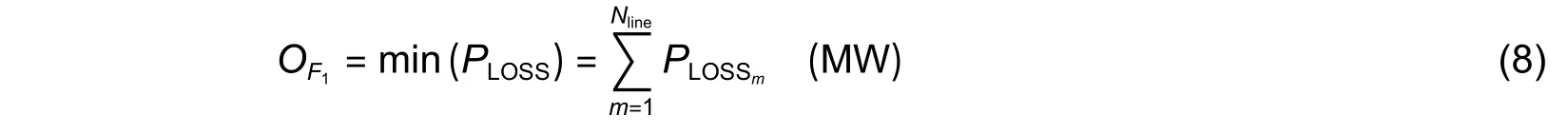
wherePLOSSmis the real power loss in themth transmission line.

ii) Severity function

3.2.Constraints

The equality and inequality constraints can be expressed as follows:

i) Equality constraints

wherePgmis the real power of busm,PDis the real power demand, andPLis the real power loss;Qgmis the reactive power of busm,QDis the reactive power demand, andQLis the reactive power loss.

ii) Inequality constraints

• Generators constraints

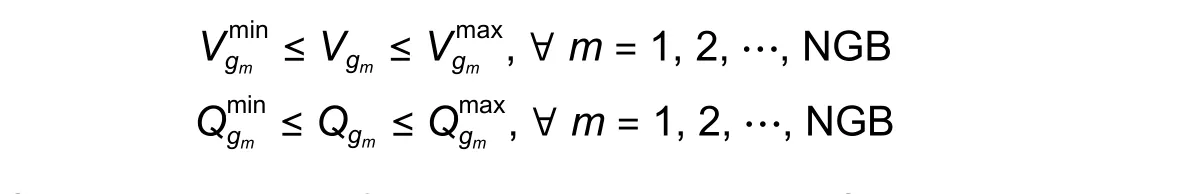
whereVgmis the voltage of generatormandQgmis the reactive power of generatorm.

• Constraints for voltages at buses and discrete transformer tap settings

whereVmis the voltage of busmandTmis the tapping setting of the transformer of busm.

• Real power generation limits

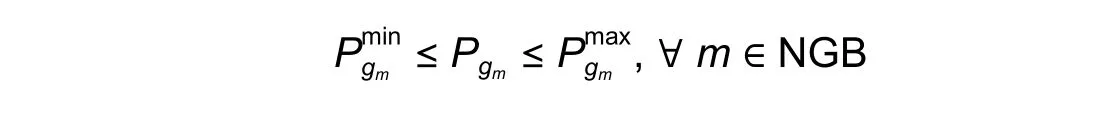
wherePgmis the real power generated by generatorm.

• Constraints for the reactive power supply from the capacitor banks:

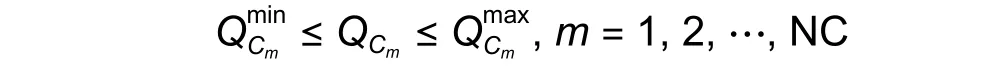
whereQCmis the reactive power supply from capacitor bankm.

• Constraints for transmission line loads:

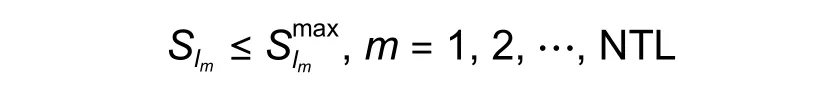
whereSlmis the line loading of transmission linem.

iii) TCSC constraints

4.SSA

Salps belong to the Salpidae family and have a similar structure and movement style as a jellyfish, i.e., by contracting, water is pumped through the body to move them forward[19].The salps shown inFig.2(a) form swarms known as “salp chains” (Fig.2(b)) which allow them to change the coordinates for foraging.Basically, the salp swarm optimization algorithm is inspired by the navigation and foraging behaviors of salps in their natural habitats.

Mathematically, salp chains can be modeled by initially dividing the population into two groups, a leader and followers, where a leader is a salp that presents at the creation of the chain and leads the movement, which is then followed by the followers.Heremstores the position of the salps in two dimensions andFis the food source targeted by the salps.The position of the leader can be updated using the following equations:

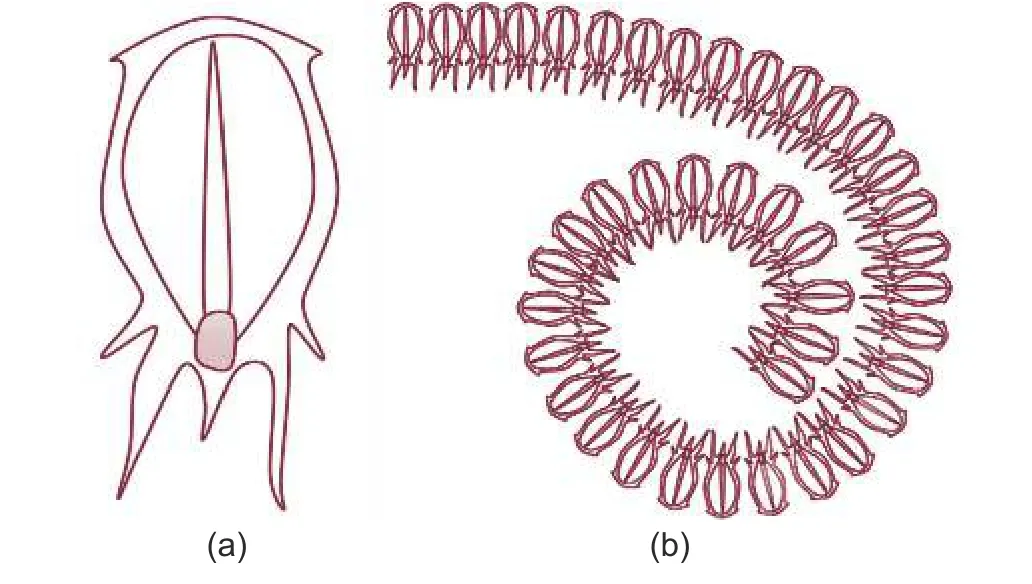
Fig.2.Salp and salp chain: (a) single salp and (b) salp chain.

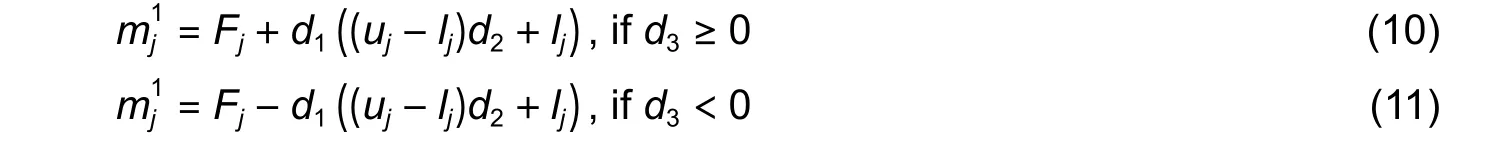
where,Fj,lj, andujare the positions of the leader, the food source, and the lower and upper bounds in thejth dimension, respectively, whereasd1,d2, andd3are random numbers, andd1maintains a balance between exploration and exploitation, which can be defined as follows:

wheretandTrepresent the current and maximum numbers of iterations, respectively.Thereafter, the position of the followers can be updated using the following equation:

wherei≥2 andis the position of theith follower in thejth dimension.By using (10),(11), and (13), salp chains can be simulated.The pseudo code of SSA is shown asTable 1.The flowchart of SSA is shown inFig.3.

Table 1: SSA

5.Results and Analysis

5.1.lllustrative Example 1

The proposed SSA is aimed at resolving the OPF problem.To test the effectiveness of the proposed algorithm within a power system, it is evaluated based on the standard IEEE-30 bus system.Generally, the IEEE-30 bus system consists of six generators placed on buses 1,2, 5, 8, 11, and 13; four off-nominal tap ratio transformers placed between buses (6-9), (6-10), (4-12), and(27-28); and two shunt capacitors placed at buses 10 and 24.For each objective, the proposed algorithm performed up to 100 iterations.The system data, including bus data, line data, and generator data, are adopted from [20].

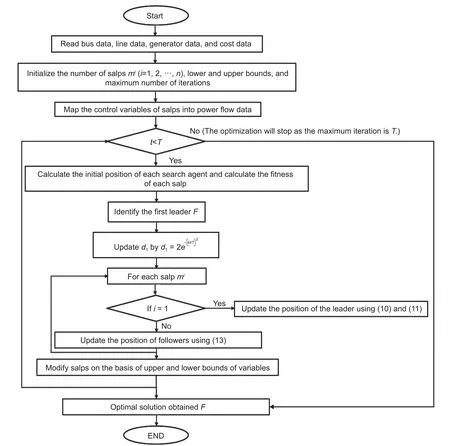
Fig.3.Flowchart of SSA.

The transmission line is validated using the SSA method, and the results are compared with those using the existing methods, such as the artificial bee colony algorithm (ABC).The OPF results for the minimization of the transmission line loss is tabulated inTable 2.It is evident that the transmission line loss are minimized using the SSA method in comparison with the existing methods.The convergence characteristics of the proposed method are also compared with those of the existing methods, as shown inFig.4.It can be observed that the proposed method achieves a better value for the objective functions in question, with an effective convergence obtained with fewer iterations.

5.2.lncorporation of TCSC

More analysis is then performed for the transmission line loss and the severity factor with the incorporation of TCSC.In accordance with the existing literature, TCSC was placed between buses (3-4).The results obtained for the considered objectives are presented inTable 3.It is clear that without any FACTS device, the transmission line loss is 2.962 MW and the initial severity factor is 1.436, which are minimized to 2.916 MW and 1.344, respectively, with the incorporation of TCSC.Thus, it can be concluded that the performance of the power system is improved with the incorporation of TCSC.The convergence curves for both the objective functions are shown inFigs.5and6.The effectiveness and improved performance of the proposed algorithm with the incorporation of TCSC can be clearly observed.

Table 2: OPF results for the minimization of the transmission line loss in the IEEE-30 bus system

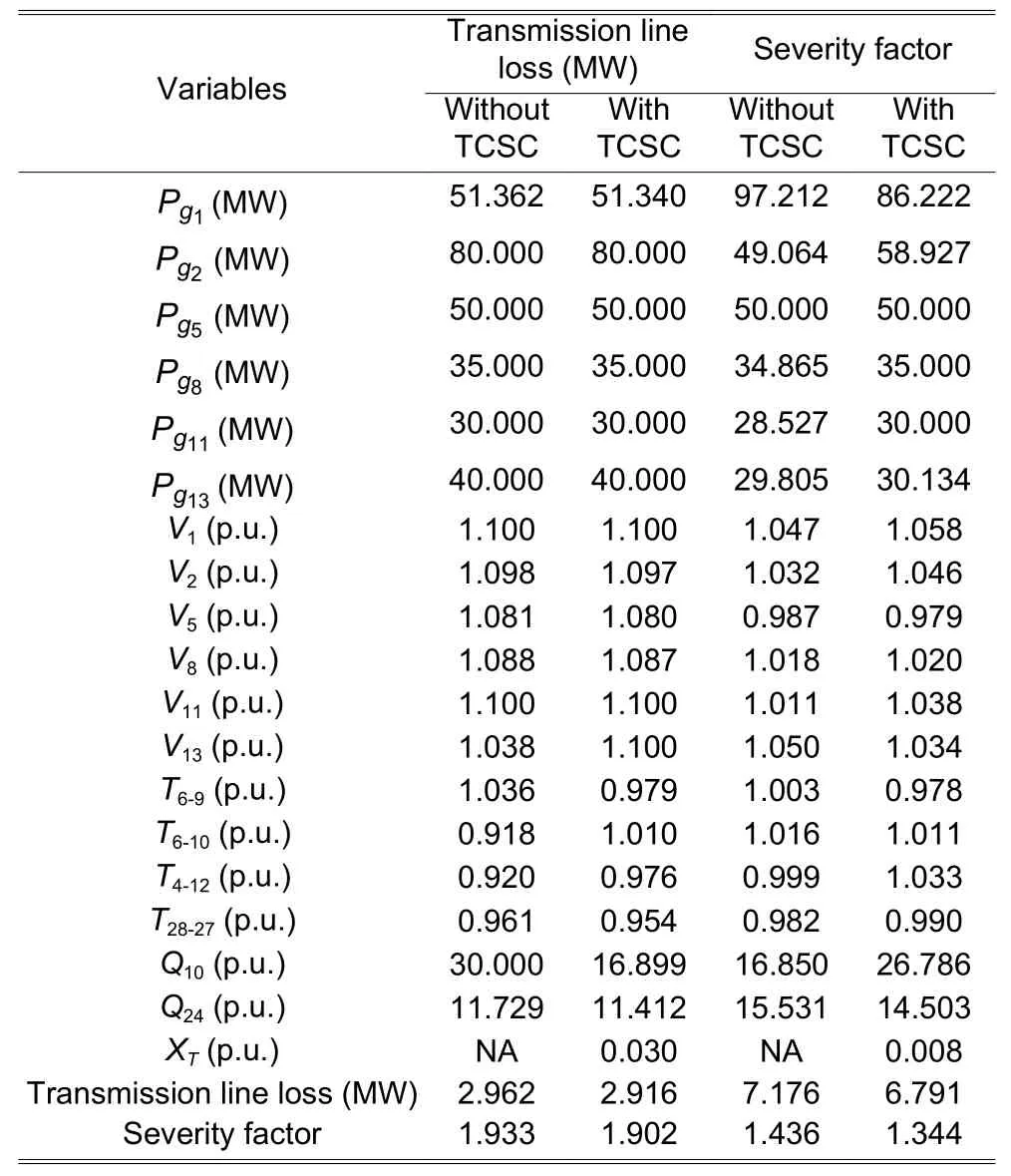
Table 3: OPF results for the transmission line loss and severity factor with and without TCSC

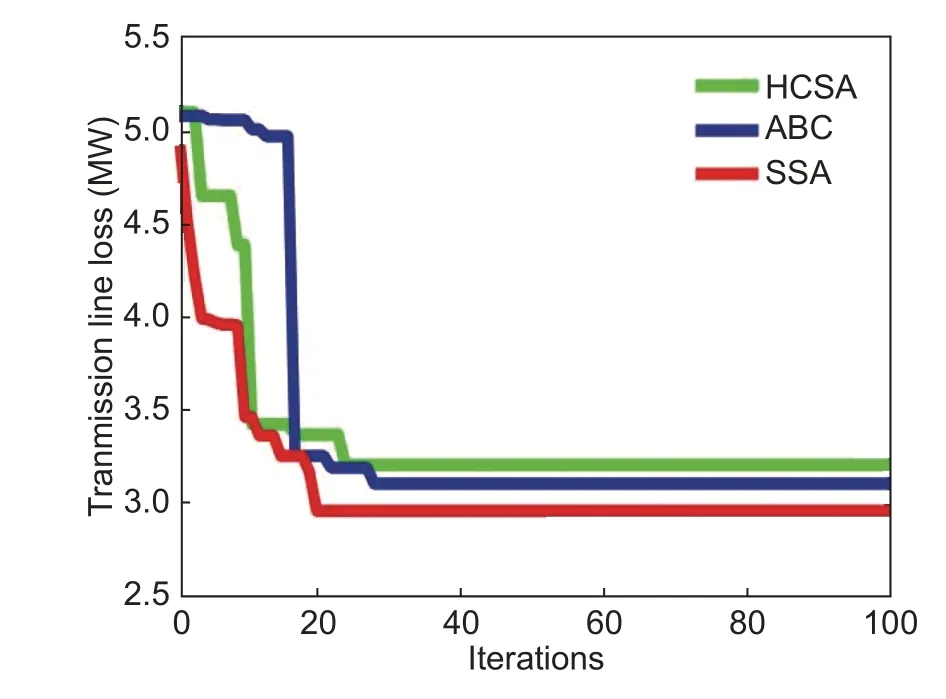
Fig.4.Convergence curve for transmission line loss.

Fig.5.Convergence curve for transmission line loss with and without TCSC.

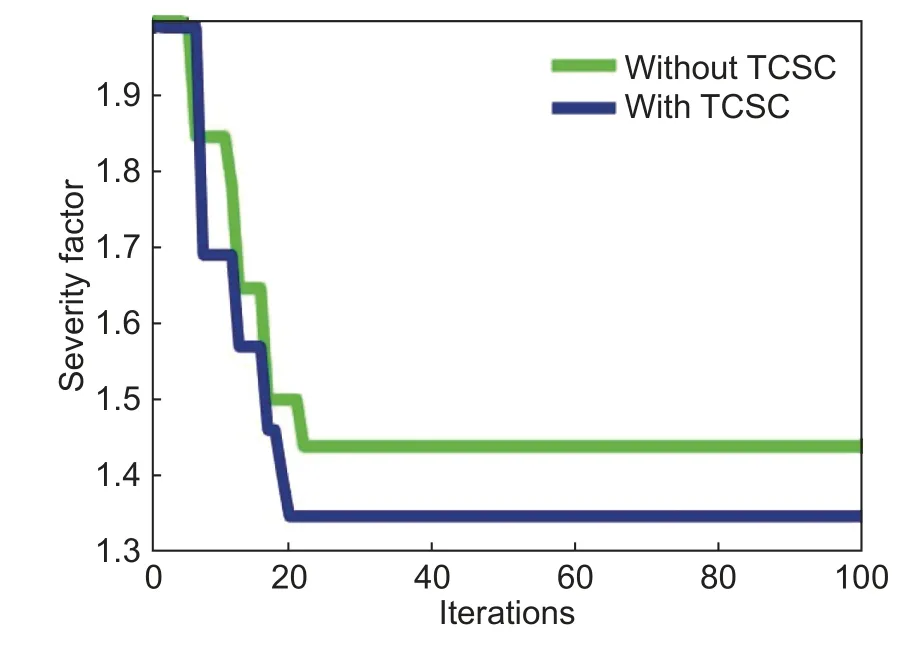
Fig.6.Convergence curve for severity factor with and without TCSC.

6.Conclusion

This paper demonstrated the application of SSA for resolving the OPF problem of power systems with some equality and inequality constraints.It was shown that SSA effectively optimized the transmission line loss and severity factor compared with the existing algorithms and that it also maintained an excellent balance between exploration and exploitation.Following the validation of SSA,TCSC was incorporated within the power system.And it was observed that the considered objective functions were further minimized, which demonstrates that the implementation of SSA with the incorporation of TCSC will provide a better solution for the OPF problem.In the future, multi-objective SSA (MSSA) could be used to resolve the multi-objective problems in power systems.

Disclosures

The authors declare no conflicts of interest.