万米AUV 下潜深度估算研究

汪明星，常津铖，任 翀，陈朝晖，*

（1.中国海洋大学海洋高等研究院 物理海洋教育部重点实验室，山东 青岛 266100；2.青岛海洋科学与技术试点国家实验室，山东 青岛 266237）

深渊海沟通常是指深度在6 000 m 以下的海沟区域[1]，主要分布在太平洋、大西洋及印度洋，是地球上未被人类全面系统感知和利用的地理空间之一，被誉为21 世纪人类可持续发展的战略“新疆域”。深渊海沟环境以高压、低温、无光黑暗、构造活跃、地震密集、生命奇特为特点，蕴含着复杂的海洋动力、地质、生物和化学等过程，它们彼此之间相互作用构成了复杂的海沟深渊过程，与地球深部之间存在着广泛的物质和能量交换，构成了地球系统中独特的组成部分[2-3]。深渊海沟是海洋科学研究的前沿领域，通过前期观测研究表明，与开阔大洋相比，深渊海沟具有更加丰富的物质输运过程[4]，深海物质输运和能量交换调控机制亟待揭示。深渊海沟具有特殊的微生物种群结构和异养代谢过程[5-6]，在驱动深海生物地球化学循环中可能发挥独特的作用[7]，对研究全球气候变暖、全球碳循环都有重要作用[8]，亟需明确海沟生命过程和生源要素之间的相互作用关系。同时在地球上最深的海沟中发现了严重的污染现象，在马里亚纳海沟和克马德克海沟调查中发现，端足类动物的脂肪组织中含有大量的持久性有机污染物（Persistent Organic Pollutants，POP），包括常用作电解液的多氯联苯（Polychlorinated Biphenyls，PCB），以及常用作阻燃剂的多溴二苯醚（Polybrominated Diphenyl Ether，PBDE）等[9]，严重地危害了全球深渊生态系统。针对上述科学问题，亟需加强对深渊海沟的系统观测，提升对深渊科学的认知水平。

由于对深海观测技术的高度依赖，深渊海沟是目前海洋科学中研究最为薄弱的环节，深渊观测的先进技术和基础设施是未来开展深渊研究的基本保证。然而，上万米的深度带来了巨大的静水压强，对深渊观测技术提出了极大挑战。迄今为止，能够开展全水深深渊探索的方式主要有海洋科考船和潜水器两种。科考船能够同时为传感器供应电力、通讯、定位、计时等，是最常用的观测平台之一。随着技术的进步，目前的科考船观测能力已经得到了极大提高。船上搭载的万米高精度温盐深仪（Conductivity-Temperature-Depth，CTD） 可开展深渊水文观测，船载多波束可开展水深探测，船载多学科调查仪器可以对水体和生物进行采样[10]。随着自治技术在海洋观测中的应用和发展[11]，潜水器在安全性、经济性和操作性方面的优势使其逐渐成为深渊探索的利器，其主要分为载人型和无人型。载人型潜水器（Human Occupied Vehicle，HOV）从20世纪60 年代开始发展[12]，国际上最大下潜深度可达10 928 m[13]；随着深远海战略的实施，我国深海技术研发和科学研究能力得到了极大提升，HOV更是经历了近20 年的跨越式发展，7 000 m 级“蛟龙”号、万米级“奋斗者”号等HOV 相继问世，提升了我国深海观测能力。水下无人潜水器（Underwater Unmanned Vehicle，UUV）又可分为遥控潜水器（Remote Operated Vehicle，ROV）、自主潜水器（Autonomous Underwater Vehicle，AUV） 和混合型潜水器等。受到各种条件限制，直到最近十年，我国深海远程遥控潜水器技术才取得了长足进步，紧跟世界先进水平，先后研制成功“海星”系列、“海马”号、“深海科考”型、“海龙”号等ROV[14]，“海斗”号、“海神6000”号等系列深海AUV，以及以“海燕”为代表的万米水下滑翔机等[15]。

马里亚纳海沟是由太平洋板块自东向西俯冲于菲律宾板块之下而形成的一条近南北延伸的深沟[16]，最大水深超过10 000 m，是世界上最深的海域[5]。海沟南段呈现出近东西延伸的特征，被称为“挑战者深渊”[17]。随着系列关键技术的攻关，国内外多款万米级潜水器先后在此开展海上试验，获取了系列科学数据，马里亚纳海沟就此成为理想的天然试验场。

对于AUV、水下滑翔机等无人无缆潜水器的下潜深度估算，一般都在其上或内部搭载调查仪器（CTD 等），通过仪器获取的温度、电导及压强数据，进行数据校正及深度数据求解[15]。常用的深度计算依据包括1980 年发布的海水热力学方程（International Equation of State of Seawater，EOS-80）、2010 年最新发布的海水热力学方程（International Thermodynamic Equationof Seawater 2010，TEOS-10）。前人研究表明，由于EOS-80 采用了多次近似，在压强直接转换深度时，其测算深度偏差会大于TEOS-10 结果[15]。通过WOA09 气候态多年平均数据研究表明，新旧方程计算的密度之差，在全球大多数海域可超过10-2kg/m3[18]，在赤道以北的太平洋海域，尤其是本文关注的马里亚纳海沟区域，该差别更为显著，对于精度要求较高的研究中必须予以考虑。TEOS-10 通过首次提出绝对盐度，对密度进行修正，弥补了实用盐标的缺陷[19]。

本文以青岛海洋科学与技术试点国家实验室研制的万米级AUV 样机在马里亚纳海沟开展的下潜试验为例，通过AUV 搭载的CTD，获取并分析本次下潜的温盐数据，对CTD 设备性能进行了校准检验，在确保数据质量可信、CTD 设备性能可靠的基础上，采用精度更高的TEOS-10 静压近似方法，对实际下潜深度进行估算，并与EOS-80 传统方法计算结果进行对比，给出本次AUV 下潜的最大深度范围，为万米无人深潜器下潜深度科学测算提供一定参考。

1 AUV 海上试验

2021 年10 月4 日，青岛海洋科学与技术试点国家实验室搭载“东方红3”船西太重大研究计划NORC2021-582 航次，在（11˚19.536′N，142˚ 9.882′E） 对自主研制的全海深无人自主潜水器（AUV）开展了万米级海试（图1、表1、图2）。该海域位于马里亚纳海沟“挑战者深渊”西南方位，由10 500 m 等深线圈闭，最深处可达10 878 m。海试期间（图2），AUV 搭载CTD（型号：SBE16 Plus，序列号：50294，最大允许下潜深度10 500 m）记录温盐数据；按照设定程序开启推进器低速助推，螺旋下潜至设定深度后启动一级抛载装置，随后按照设定方位航行；14 时49 分，AUV 下潜到最大深度，推进器停止工作，AUV 自由上浮出水。AUV 按预设程序完成全部动作，成功获取了完整的万米温盐深数据及万米深海影像资料。

图2 海试现场照片

表1 AUV 海上试验概况

图1 作业站位附近的海底地形图

2 CTD 数据分析

本文主要研究万米无人深潜器的深度估算方法，以使深度估算结果更具科学性和可信度。为保障后续深度估算的顺利开展，需要先对本次试验CTD 获取的数据质量进行评估，对CTD 数据质量进行分析，并与前人在相关海域获取的温盐数据特征进行对比分析。将CTD 剖面数据经过低通滤波、热通量订正、逆压消除等操作[20]，得到质量控制后的下降及上升剖面的温度、电导率及压强数据（图3），图3（a）、图3（b）、图3（c）分别表示温度随时间变化、电导率随时间变化、压强随时间变化。由于下降、上升剖面在水平方向相距百米以内（表1），所以空间因素造成的温盐差异很小。由于上升期间压力传感器存在回程误差，后续数据分析均取用下降时的剖面数据。

图3 CTD 的下降/上升温盐剖面图

海水在混合层的温度为29.860~29.880 ℃（图4），该范围在混合层内保持相对稳定；在温跃层的海水温度迅速降低到20.880~29.082 ℃，这是由于多种海洋动力过程的共同调制作用导致；在温跃层以下，压强3 000~5 000 dbar 范围处，海水的温度逐渐降低至1.470~1.650 ℃，海洋温场的长周期变化占据主导作用；当压强继续增大时，底层10 000~10 196 dbar 处，海水的温度可升至2.234~2.270 ℃，这是由于绝热压缩导致海水温度缓慢升高[21]。温度对电导率的作用远大于盐度，因此电导率的变化趋势与温度相似，随着温度在深层变得相对稳定，盐度对电导率的贡献变大。海水在混合层的实用盐度在从34.354 0 PSU 增加到34.395 3 PSU；在温跃层中，海水实用盐度继续从34.410 5 PSU 增加到34.907 5 PSU；中层海水3 000~5 000 dbar 到底层10 196 dbar，海水的盐度增加范围为0.000 9~0.029 7 PSU。

图4 温盐剖面图

通过上述数据分析，本次试验所获取的CTD数据与前人在相近区域中的研究结果基本相符[15]，数据质量基本可信。

3 CTD 传感器校准检测

为对AUV 下潜深度做精确估算，还需要评估本次试验所用CTD 的设备性能情况，鉴于此，本文进一步对用于获取温盐数据的CTD 传感器进行了性能校准检测。按照JJG 763—2019《温盐深测量仪计量检定规程》要求，结合国际一流检定校准体系，对CTD 进行实验室校准测试，以确保符合性能指标要求。此款CTD 性能指标参见表2，其温度测量范围在-5~35 ℃，初始精度±0.005 ℃，每月漂移0.000 2 ℃；电导测量范围在0~9 S/m，初始精度±0.000 5 S/m，每月漂移0.000 3 S/m。对CTD 进行温度、电导校准，通过测定的示值误差和重复性来表征传感器性能。

表2 CTD 性能指标

3.1 温度示值误差和温度测量重复性检测

CTD 校准检测过程需要保持恒温恒湿环境，将环境温度设为21.4 ℃，湿度设为60%。按照CTD性能指标要求，在1~32 ℃之间取10 个温度点，进行温度试验。先将恒温水槽温度控制在32 ℃，恒温保持，同时将标准铂电阻温度计和CTD 置于恒温水槽中，标准铂电阻温度计尽量靠近CTD 温度传感器位置；待校准点上的温度稳定后，测温电桥与CTD 同时测量3 min，获取不少于10 组读数，取对应温度读数的算术平均值分别作为该校准点上的标准温度值和CTD 温度示值，作差得到该温度点示值误差。选取温度测量重复性的校准点为16 ℃，待校准点上温度稳定后，重复上述操作，完成至少6 次测量。

在选取的10 个温度点中，CTD 温度传感器示值误差在±0.005 ℃上下波动，结合传感器每月漂移参数，判定温度传感器性能基本符合传感器精度要求；CTD 温度传感器在16 ℃时的测量重复性为0.000 4 ℃，符合一级CTD 温度传感器测量重复性要求。

3.2 电导示值误差和电导测量重复性检测

电导校准时环境压强为1 021.79 hPa，盐度计设定温度为24 ℃，电导示值误差与温度示值误差同时在恒温水槽中进行。待校准点上的温度稳定后，CTD 电导率测量3 min，获取不少于10 组读数，同时用取样管取海水样品1 瓶，盖紧瓶盖并编号待用；以IAPSO（International Association for the Physical Sciences of the Ocean）标准海水为参照，用盐度计测量海水样品，每瓶海水样品测量3 次，取其算数平均值作为该校准点的电导率值。电导率测量重复性与温度测量重复性同时在恒温水槽中进行，完成至少6 次测量。

根据标准温度、标准电导值、CTD 电导传感器电导值，计算得到电导示值误差在-8.50×10-4~4.25×10-3S/m 之间，结合传感器每月漂移参数，符合CTD 电导传感器指标要求；电导传感器在16 ℃时的测量重复性为0.000 3 S/m，符合一级CTD 电导传感器测量重复性要求。

根据以上校准检测试验，确认参与本次试验的CTD 温度、电导传感器均符合技术指标要求，CTD设备性能良好。本次海试在CTD 设备指标范围内开展，CTD 设备性能可靠。在分析数据质量可信、检测CTD 设备性能可靠之后，对下潜深度的估算才更加严谨。

4 下潜深度估算

对于下潜深度估算，目前常用的两种海水热力学方程包括：1980 年认可的国际海水状态方程EOS-80，以及2009 年由联合国教科文组织政府间海洋学委员会（UNESCO-IOC）第25 次大会决议通过的最新版本国际海水热力学方程TEOS-10。与EOS-80 相比，TEOS-10 最明显的变化是采用绝对盐度代替实用盐度，其显著优点是引入Gibbs 函数，并第一次能够系统地考虑海水成分的空间变化，这种变化对开放大洋中的水平密度梯度影响不可忽略。本文分别基于EOS-80 传统方法和TEOS-10 静压近似方法开展下潜深度估算，并对估算结果进行分析讨论。

4.1 EOS-80 传统方法估算

1976 年，SAUNDERS P M 等[22]提出了一个压强和深度转换的函数关系，见式（1）。为了阐述得更为简单一致，1981 年，SAUNDERS P M 基于“国际海水状态方程（EOS-80）”开发了一个更简单，但精度却较低的二次深度公式。

式中，g0（φ）表示海表面重力，是纬度的函数；γ是重力的平均垂直梯度；V是比容；ΔD是位势异常。

上述精确公式涉及四阶压强最小二乘多项式，不便于常规应用，为进一步简化，将四阶压强最小二乘多项式拟合到从精确公式计算出的0~12 000 dbar范围内的数值表中，参见式（2）。

式中，c1= 9.726 59；c2= -2.251 2×10-5；c3=2.279×10-10；c4=-1.82×10-15。

最小二乘公式消除了计算对数的需要，完整的公式形式参见式（3）[22]。

式中，z是深度；p是压强；g（φ）是随纬度φ变化的重力加速度；γ′是修正的重力加速度的垂向梯度；ΔD是位势异常。Gibbs 软件库（Gibbs-SeaWater library of computer software， GSW） 中gsw_z_from_p（p，lat） 函数使用的即为EOS-80 传统方法，通过调用此函数，不考虑压力传感器误差时，计算得到深度为9 911.5 m；将压力传感器误差计算在内（可允许最大误差为±0.1%FS），每循环一次使用一个随机误差，取300 组随机误差循环，估算深度范围为9 901.5~9 921.4 m，由于每次循环所取随机数不同，计算结果会有极小波动，计算结果呈均一性分布，如图5 所示。

图5 考虑仪器误差采用EOS-80 传统方法估算得到的下潜深度范围

4.2 TEOS-10 静压近似方法估算

EOS-80 传统方法仅是下潜最深处压强p和随纬度变化的重力加速度g（φ）的函数，未将重力加速度随压强变化考虑在内，也未考虑整个剖面温盐分布情况，估算精度有待提高。为了准确评估此次AUV 样机性能，需要精确计算其下潜深度，本文采用国际上最新的海水热力学方程TEOS-10 静压近似方法对深度进行估算。CTD 每10 s 采样一次，每10 s 下放的水体视为一个流体微团，每一个流体微团的压强用p表示，对其进行全剖面积分，参见式（4）。在估算过程中，将密度ρ（SA，t，p）、重力加速度g（φ，p）及仪器误差等因素充分考虑在内，得到更为精确的下潜深度值及深度范围。

使用差分法，将每10 s 下放的水体视为一个流体微团，将全剖面深度进行划分，默认第i个水柱的ρigi与第i-1 个水柱的ρi-1gi-1近似相等，则可得第i个水柱的深度，参见式（5）。

4.2.1 密度

海水密度ρ是绝对盐度SA、实测温度t、实测压强p的函数，函数关系可表示为式（6），使用GSW中的gsw_rho（SA，t，p） 函数即可实现此运算。温度t、压强p均可通过CTD 实测得到，绝对盐度SA的计算引入Gibbs 函数，通过实用盐度推导得出，参见式（6）。

式中，g为Gibbs 函数。

（1）绝对盐度SA求解

绝对盐度SA习惯上被定义为海水中溶解物质的质量分数。在一系列研究中发现[23-26]，通过海水样本密度的精确测量值，以及这些样品的实用盐度，可以计算出世界大洋中大多数海盆中δSA=SASR的值。这个方法首先通过TEOS-10 状态方程，将基准盐度作为盐度变量，计算得到“基准密度”。利用实测密度和基准密度之间的差异来计算绝对盐度偏差δSA=SA-SR[27]。MCDOUGALL T 等[28]算法是基于SA-SR数据与海水样本中硅酸盐浓度[27]之间的相关关系计算得到，硅酸盐则由世界图集[29]差值得到。计算绝对盐度采用的公式最终表述如下，调用GSW 中的gsw_SA_from_SP 函数即可实现此计算。绝对盐度SA是关于实用盐度Sp的函数，见式（7）。

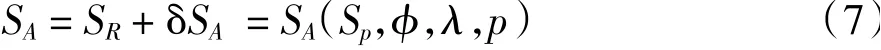
式中，Sp为实用盐度；φ是纬度（北纬为正）；λ是经度（东经算起，范围是0˚~360˚）；p是海水压强（dbar）。

（2）实用盐度Sp求解

实用盐度Sp是关于电导率的函数。电导率比定义见式（8）。

式中，C（35，15，0）是实用盐度35 PSU、温度15 ℃、大气压条件下的电导率。通过转化，R可分为3 个部分，详见式（9）。

式中，Rp和rt均可通过计算得到；Rt为海水在标准温度值下的电导比值。

根据PSS-78，实用盐度可由以下方程进行计算，该方程在-2~35 ℃，实用盐度2~43 PSU 范围内都适用，建立Rt与实际盐度的函数关系，见式（10）。

式中，系数k=0.016 2；ai和bi都是可查得的已知系数。

通过此函数关系调用GSW 中的gsw_sp_from_c函数，计算得到实用盐度Sp。

4.2.2 重力加速度

TEOS-10 采用热力学势描述海水、冰和湿空气属性，可以比EOS-80 导出更多的热力学属性。本文优先参照TEOS-10 静压近似方法，重力加速度与纬度、压强/深度的函数关系可以表述如下（详见http：//teos-10.org/pubs/gsw/pdf/grav.pdf）。

式中，g为重力加速度；φ是纬度（北纬为正）；p是海水压强（dbar）。

运用以上函数关系，通过GSW 中的gsw_grav函数实现由压强到重力加速度的求解。

4.2.3 仪器误差

CTD 本身存在仪器误差，温度为±0.005 ℃，电导为±0.000 5 S/m，压强为0.10%FS，并伴有每月漂移。电导率通过影响绝对盐度，从而影响密度计算，温度影响密度计算，压强则直接影响深度求解。

4.2.4 计算结果

为深入探究密度、重力加速度和仪器误差对本次AUV 试验的下潜深度影响，得到更为精确的下潜深度值及深度范围，将以上因素全部考虑在内，采用TEOS-10 静压近似方法计算得到结果如下。

（1）为将TEOS-10 静压近似方法与EOS-80 传统方法计算结果直接对比，直接取实测温度、电导、压强值，取g（φ）为随纬度φ变化的重力加速度，进行计算，得下潜深度为9 930.2 m。

（2）采用TEOS-10，运用静压近似法计算，取实测温度、电导、压强值，取g（φ，p）为重力加速度；φ是纬度（北纬为正）；p是海水压强（dbar），求得下潜深度为9 919.0 m。

（3）采用TEOS-10，运用静压近似法，考虑仪器误差，取g（φ，p）为重力加速度计算；φ是纬度（北纬为正）；p是海水压强（dbar）。其中，仪器误差通过以下方式获取：CTD 每10 s 采样一次，由于仪器误差的存在，CTD 每次采样，其温度传感器读数会在±0.005 ℃范围内随机改变，电导传感器读数会在±0.000 5 S/m 范围内随机改变，每个计算剖面固定一个随机压强误差（±0.1%FS），每循环一次使用一个随机压强误差，取300 组随机误差循环，求得下潜深度范围为9 908.9~9 929.0 m，由于每次循环所取随机数不同，计算结果会有极小波动，深度结果在此区间内呈均一性分布（图6）。由于充分考虑海水成分的空间变化、重力加速度随海水压强变化和仪器误差等多种影响要素，认为由此思路下求取的结果置信度最高。相比较EOS-80 传统方法求得的深度结果9 901.5~9 921.4 m，TEOS-10 静压近似方法求取结果平均比传统方法求取的深度范围差7~8 m。

图6 考虑仪器误差时采用TEOS-10 静压近似方法循环运算300 组得到的深度范围分布

对TEOS-10 静压近似方法与EOS-80 传统方法估算结果进行比较（图7），蓝色曲线a 表示采用TEOS-10 方程使用静压近似方法，由温度、电导、压强实测值、g（φ，p）计算求解得到的深度值（左侧纵坐标表征）；橙色曲线b 表示采用EOS-80 传统计算方法，由温度、电导、压强实测值、g（φ）计算得到与a 的深度差（右侧纵坐标表征）。对比发现，随着海水压强增大，重力加速度随压强变化明显，其对深度估算的影响逐渐从0 m 增加到11 m 以上，所以在深渊观测中，不可忽略重力加速度随压强增大的影响。本次AUV 的精确下潜深度为9 919.1 m，并在9 908.9~9 929.0 m 内置信度最高。

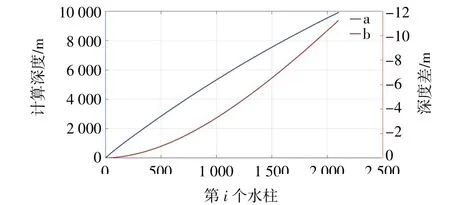
图7 TEOS-10 静压近似方法与EOS-80 传统方法计算结果比对

4.2.5 密度、重力加速度、仪器误差等要素对深度估算的影响分析

在TEOS-10 静压近似方法计算中，（1）密度对深度估算的影响：通过将每10 s 下放的水体视为一个流体微团，每一个流体微团的密度单独计算，后对其进行全剖面积分，得到的下潜深度为9 930.2 m，与EOS-80 传统方法计算结果9 911.5 m 相比，计算深度增加18.7 m；（2）重力加速度对深度估算的影响：重力加速度是纬度和压强/深度的函数，EOS-80 传统方法中仅考虑纬度对重力加速度的影响，这在浅层海水中影响并不大，但是在万米无人深潜中，万米水深对重力加速度的影响会非常明显，考虑重力加速度的影响后，下潜深度的计算结果由9 930.2 m 修正为9 919.0 m，这主要是由于随着压力/水深增加，重力加速度变大导致；（3）仪器误差对深度估算的影响：在仪器允许误差范围内，对温度和电导的测量误差，通过影响实用盐度、绝对盐度计算结果，从而影响密度的求解，合并压力测量误差后，综合影响深度求解，在仪器允许误差范围内，下潜深度得到一个估算范围为9 908.9~9 929.0 m。

5 结 论

本文以2021 年青岛海洋科学与技术试点国家实验室研制的万米级AUV 样机在马里亚纳海沟开展的下潜试验为例，通过AUV 搭载的温盐深仪（CTD），分析了本次下潜获取的温盐数据，并对搭载的CTD 性能进行了校准检验，在确保数据质量可信、CTD 设备性能可靠的基础上，分别采用EOS-80 传统方法及TEOS-10 静压近似方法，对实际下潜深度进行计了估算讨论，为万米无人深潜器下潜深度科学测算提供一定参考。EOS-80 传统方法和TEOS-10 静压近似方法对比如下。

使用EOS-80 传统方法：不考虑压力传感器误差时，计算得到深度为9 911.5 m；考虑压力传感器误差时，求得深度范围为9 901.5~9 921.4 m。使用TEOS-10 静压近似方法：取重力加速度仅随纬度变化，计算得到下潜深度为9 930.2 m；取重力加速度为纬度与海水压强的函数，求得下潜深度为9 919.0 m；取重力加速度为纬度与海水压强的函数，考虑仪器误差，求得下潜深度范围为9 908.9~9 929.0 m。由于EOS-80 传统方法经过多次近似，在实际计算中，只需最深处压力值和所在经纬度下的重力加速度，即可计算得到最大下潜深度，所以在追求计算效率、同时对计算精度要求不高的情况下，可以优先选用EOS-80 传统方法；然而如果在对精度要求更高的研究中，尤其是万米下潜时，密度、重力加速度等要素影响不可忽略时，使用TEOS-10 静压近似方法则更为准确。

通过以上估算发现，TEOS-10 静压近似方法将重力加速度、海水密度、仪器误差等要素均考虑在内，计算结果更为精确。本次试验中AUV 的最大下潜深度为9 919.0 m，置信范围为9 908.9~9 929.0 m，为万米无人深潜器下潜深度科学测算提供一定参考。