线性Poisson-Boltzmann方程基于L2投影的虚单元方法

陈键铧， 阳 莺

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

Poisson-Boltzmann equation(PBE)是用来描述电荷密度分布和离子浓度的偏微分方程，广泛应用于物理、生物和化学等[1]领域。PBE是一类带有分片常数和奇性的问题，常用的求解方法有有限差分法[2-3]和有限元法[4-5]等。在实际问题中，有限差分法和有限元法对于求解不规则界面时效果不佳。虚单元法由于使用多边形网格，更适合求解不规则界面问题。

近年来，虚单元方法被广泛应用于各种偏微分方程的数值求解，最初在2012年由Brezzi等[6]提出，起初被应用于Poisson方程，后来被推广到其他方程[7-8]。虚单元方法对于网格方面的要求较低，可以比较灵活地应用于不规则的多边形网格，包括非凸多边形网格。虚单元法的核心是虚单元空间中试探函数和检验函数无显式表达式，事实上，虚单元法只需局部离散函数空间的多项式子空间的知识来提供稳定和精确的数值方法。通过引入合适的投影算子，将虚单元空间的函数及其梯度映射到多项式上，从而实现投影算子仅使用虚单元空间的自由度即可计算，而刚度矩阵便是通过自由度来进行计算的。

针对线性 PBE，利用L2投影算子，设计了一种虚单元离散格式，给出了在多边形网格上的虚单元求解，并给出H1误差分析。数值实验结果验证了理论结果的正确性。

1 预备知识

考虑如下一类线性PBE：

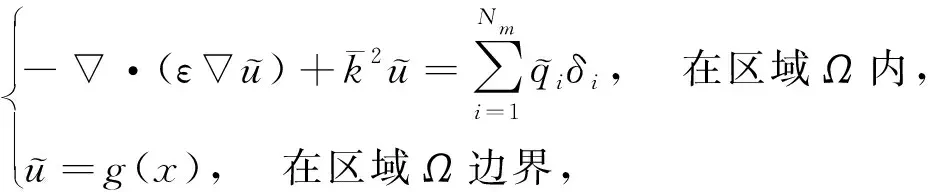
(1)

其中：

Ωm为分子区域，Ωs为溶剂区域，εs=80，εm=2，k2为Debye-Huckel参数。

其中：kB为Boltzmann常数；T为温度；qi为第i中离子的电荷量；ec为单位电荷。δi(x)=δ(x-xi)为xi处的Dirac分布。

方程(1)具有奇性，为了避免求解奇性问题， 根据文献[4]作如下分解：

(2)

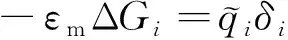
将式(2)代入式(1)，得到以下PBE：

(3)

方程(3)的弱解为u∈H1(Ω)，满足

(4)

其中：

a(u,v)=(εu,v)；

(5)

(6)

(f,v)=(·((ε-εm)G),v)。

(7)

2 虚单元空间

对任意h和E∈Γh，假设存在一个正常数λ，满足[6,10]：

1)单元E相对于半径为λhE的球是星型；

2)单元E每条边的长度大于或等于λhE。

考虑一阶的虚单元空间，首先定义E上的局部空间。对∀E∈Γh，

Δv|E∈P-1(E)},P-1(E)={0},

(8)

对应的全局空间为

(9)

2个投影算子的定义为

(Π0vh-vh，p1)E=0,∀p1∈P1(E)；

(10)

((Πvh)-vh,p1)E=0,

∀p1∈P1(E)。

(11)

双线性形式a(u,v)在单元E上的表示为

并满足如下连续性和正定性：

∀u,v∈H1(Ω)。

(12)

在单元E∈Γh上的内积形式定义[11]为

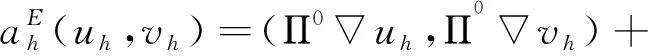
SE((I-Π)uh,(I-Π)vh),

(13)

(14)

(15)

其中，对于SE，假设存在2个正常数α*和α*，满足

α*aE(v,v)≤SE(v,v)≤α*aE(v,v),

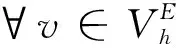
对于任意的uh,vh∈Vh, 定义

方程(3)的虚单元法离散格式：存在uh∈Vh，使得

ah(uh,vh)+bG,h(uh,vh)=(fh,vh),∀vh∈Vh。

(16)

引理1[11]对任意E∈Γh和单元E上任意函数φ，存在一个正常数C，满足

m、s∈N,m≤s≤k+1,s≥1；|φ-φI‖m,E≤

引理2[11]对任意的v∈Vh，任意整数k≥1，有

ah(v,v)≥

(17)

引理3[11]双线性形式ah(·,·)在Vh×Vh上是连续的，即

ah(uh,vh)≤C‖uh‖1‖vh‖1,uh,vh∈Vh,

(18)

其中常数C不依赖于h。

引理4[11]对任意的u∈H2(Ω)和vh∈Vh， 有

∀E∈Γh。

(19)

3 误差估计

定理1假设u∈H2(E)∩W1,∞(E)是式(4)的解，f∈H1(E)，uh∈Vh是式(16)的解，则有

‖u-uh‖1≤C(h+‖u-uh‖0),

(20)

其中C为与h无关的常数。

证明将误差e拆写成2部分，

e=u-uh=u-uI+uI-uh,

记eh=uh-uI。对式(17)运用庞加莱不等式，有

(fh,eh)-bG,h(uh,eh)-ah(uI,eh),

(21)

-ah(uI,eh)=ah(Π0u-uI,eh)-ah(Π0u,eh)=

ah(Π0u-uI,eh)-ah(Π0u,eh)+

a(Π0u,eh)+a(u-Π0u,eh)-a(u,eh)。

(22)

将式(22)中的a(u,eh)用式(4)替换，再将式(22)代入式(21)，得

bG,h(uh,eh))+(a(Π0u,eh)-ah(Π0u,eh))+

ah(Π0u-uI,eh)+a(u-Π0u,eh)=

H1+H2+H3+H4+H5。

(23)

由式(15)，有以下近似：

(24)

由式(14)，有以下估计：

H2=bG(u,eh)-bG,h(uh,eh)=

I1+I2+I3,

(25)

C‖u-Π0u‖0‖eh‖0≤Ch‖u‖1‖eh‖。

(26)

由文献[3]，u∈L∞(Ω),G∈C∞(Ωs)，有

(27)

对于I3估计，有

C‖Π0u-Π0uh‖0‖Π0eh‖0≤

C‖u-uh‖0‖eh‖1。

(28)

将式(26)～(28)代入式(25)，可得

H2≤C(h(‖u‖1+1)+‖u-uh‖0)‖eh‖1≤

C(h+‖u-uh‖0)‖eh‖1。

(29)

由式(19)可得

H3=a(Π0u,eh)-ah(Π0u,eh)=

(30)

由式(18)得

H4=ah(Π0u-uI,eh)≤

‖Π0u-uI‖1‖eh‖1≤Ch‖eh‖1。

(31)

由式(12)，有

H5=a(u-Π0u,eh)≤

‖u-Π0u‖1‖eh‖1≤Ch‖eh‖1。

(32)

将式(24)、(29)～(32)代入式(23)， 可推得式(20)成立。证毕。

4 数值实验

用数值例子验证虚单元法的有效性，基于文献[12-13]代码进行计算。

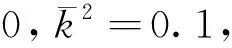
图1为三角形四边形五边形混合的多边形网格。图 2、3为虚单元法在图1网格上的解与数值解的L2和H1模误差图像，该图像在对数尺度下给出。根据文献[14]，分别给出L2、H1模定义：

‖Πu*-Πuh‖0，|Πu*-Πuh|1。

从图2、3可看出，L2模误差达到二阶，H1模误差达到一阶，与理论相符。由于问题(4)的解很小，图2、3给出的数据是原问题的1018倍。

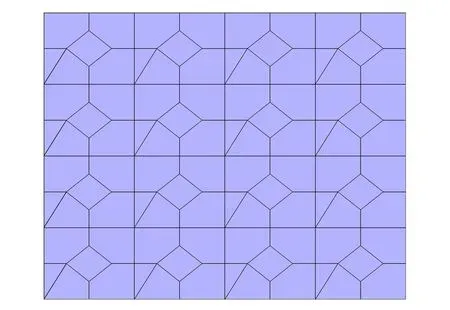
图1 三角形、四边形及五边形组成的混合多边形网格

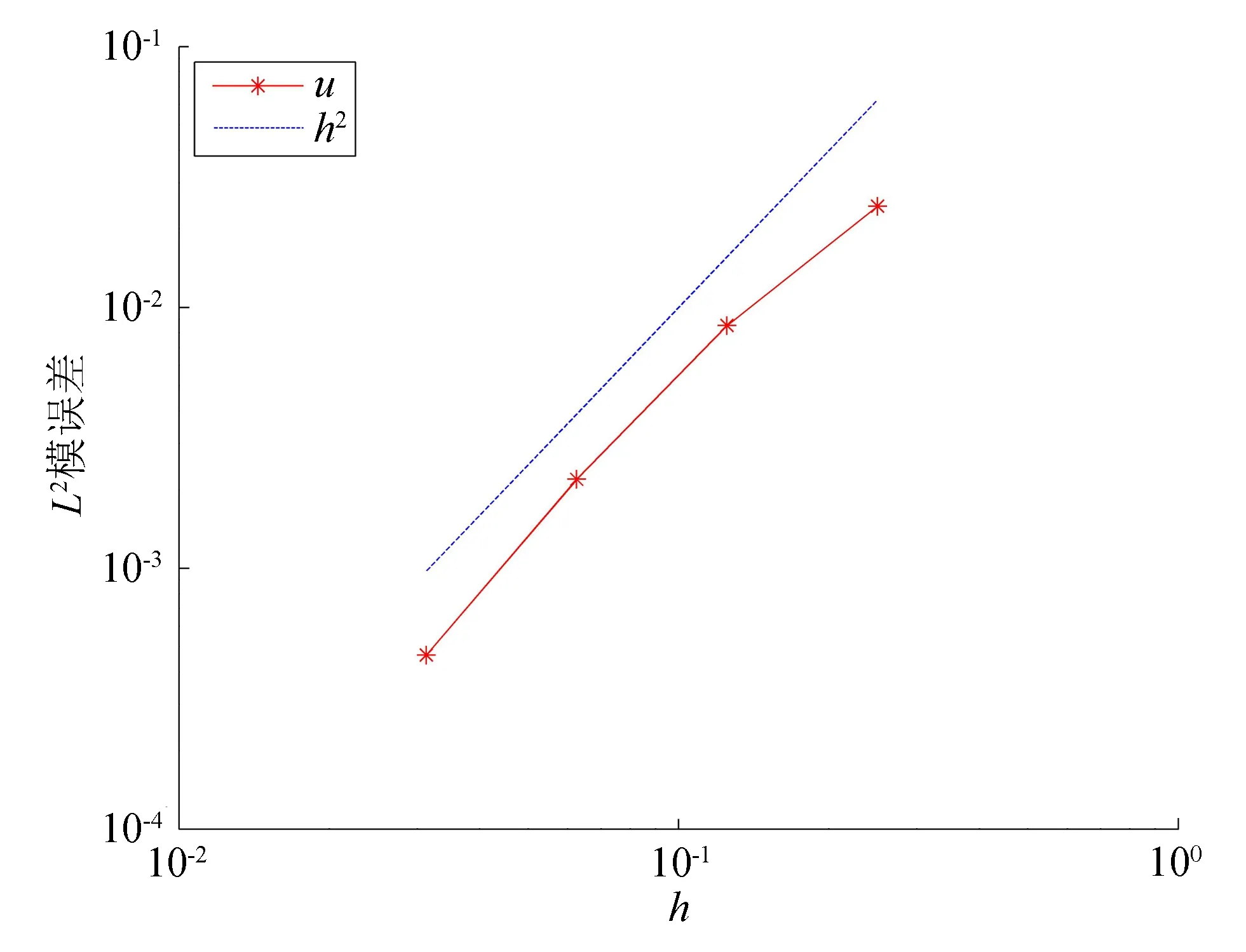
图2 L2模误差

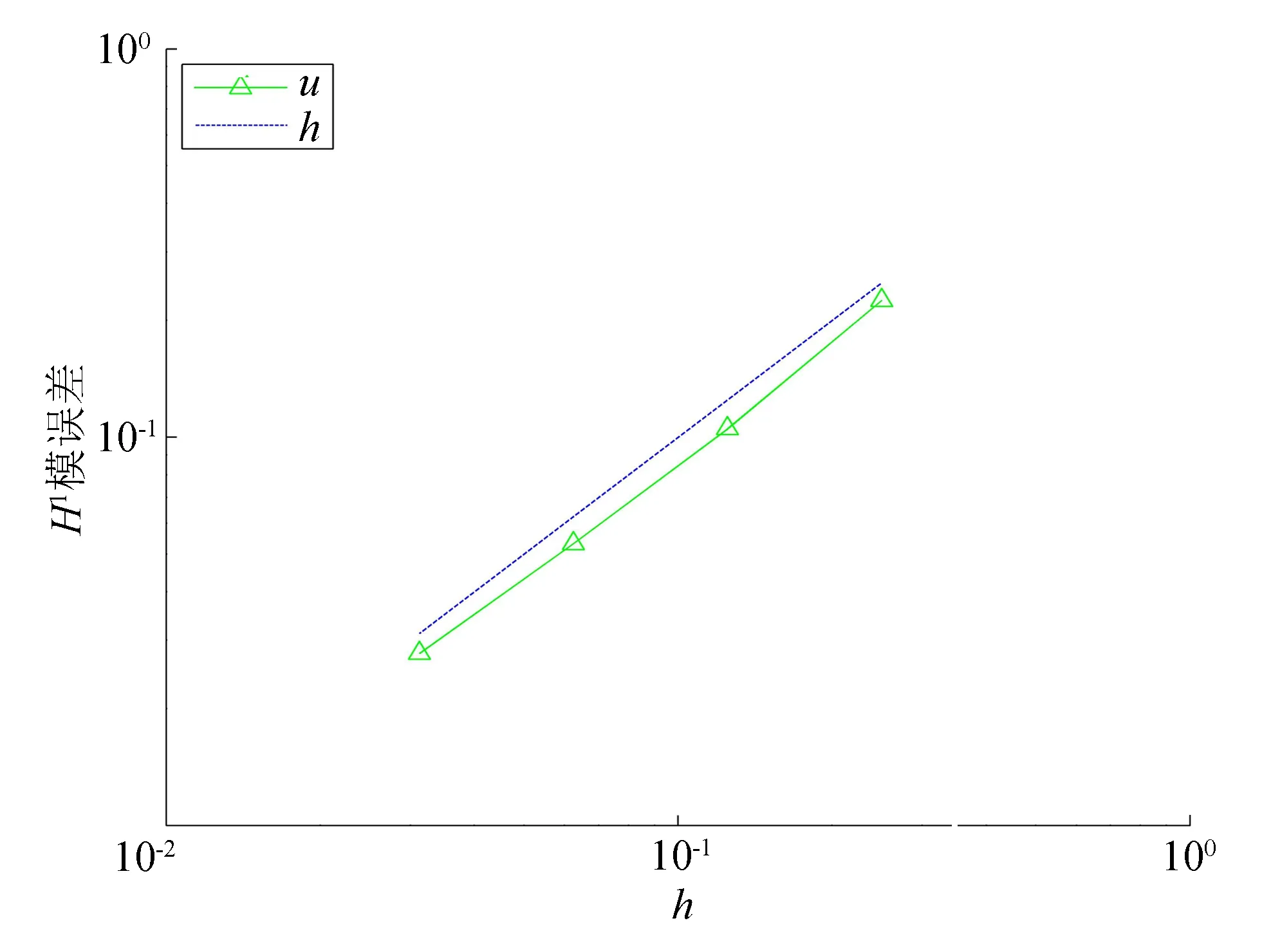
图3 H1模误差

5 结束语

针对线性PBE，利用L2投影算子，设计了一种虚单元离散格式，给出了H1范数的误差分析。数值实验结果表明了虚单元法的有效性。这一方法可进一步推广到求解非线性PBE问题中。