基于双隐含层的AGA_BP偏好课程预测模型

洪 雅 敏

(闽西职业技术学院 信息与网络中心， 福建 龙岩 364021)

0 前 言

线上线下混合教学模式是当今教育的主流。根据学习者的学习偏好，进行在线学习资源个性化推荐是实现自适应学习、提高线上学习效率的前提条件[1]。近年来，学习推荐系统[2]的研究内容主要包括学习者建模[3]、学习资源建模[4]和推荐算法等 3个方面。学习者建模主要基于不同学习者的学习偏好、学习风格、知识掌握程度和知识文化基础等特征[5]。学习资源主要包括习题、教师授课课件、教学音视频等，这些都包含在每门在线课程中。本次研究根据学习者连续14 d的学习风格，构建了一个具有双隐含层的AGA_BP偏好课程预测模型[6-8]来预测学习者的课程偏好。

1 预测模型的构建

1.1 BP模型的构建

1.1.1 样本数据

样本数据来源于368名学习者14 d(2021年 3月1日 — 14日)的在线学习记录，共6 186条数据，涉及68门课程。模型输入参数包括姓名、课程名称，以及反映学习者风格的视频观看进度、任务完成数、当天视频观看时长和当天章节学习次数等(见表1)。例如，第6 186条数据显示，个人理财规划课程共有32个任务和32个课程视频，截至3月14日秦*越已完成4个任务、已观看4个课程视频，其中3月14日当天观看课程视频 79 min、完成章节学习3次。为了进行模型训练并测试训练效果，将样本数据分为训练集、测试集和验证集，并按8∶1∶1的比例随机抽取。

1.1.2 数据预处理

在线教学平台中，学习者的学习记录包括姓名、学号、学校、专业、班级、入学年份等基本信息，以及反映学习者学习风格的课程名称、视频观看进度、任务完成数、当天视频观看时长、 当天章节学习次数、章节测验分数、讨论数等。对于新用户，章节测验分数和讨论数的数据较少。因此，通过数据预处理[9]进行数据清洗，只保留姓名、课程名称、视频观看进度、任务完成数、当天视频观看时长和当天章节学习次数等6个指标，选取后4个指标作为特征值并进行归一化处理，如式(1)所示：

(1)

式中：x—— 归一化后的特征值；

x′ —— 初始特征值；

xmax—— 特征值最大值。

由于预测结果为学习者的偏好课程，属于非数值型数据，因此对其进行one-hot编码处理。

1.1.3 BP模型结构

根据教育大数据的特点，构建一个包含2个隐含层的BP神经网络，如图1所示。在线教学平台有68门课程，体现学习者在线学习风格的指标有4个。因此，模型的输入层节点数为272个，输出层节点数为68个，而中间2个隐含层的神经元个数通过经验法和试凑法来确定。最终确定的BP神经网络模型结构为272-204-136-68。模型包括前向传播和反向传播等2个过程。

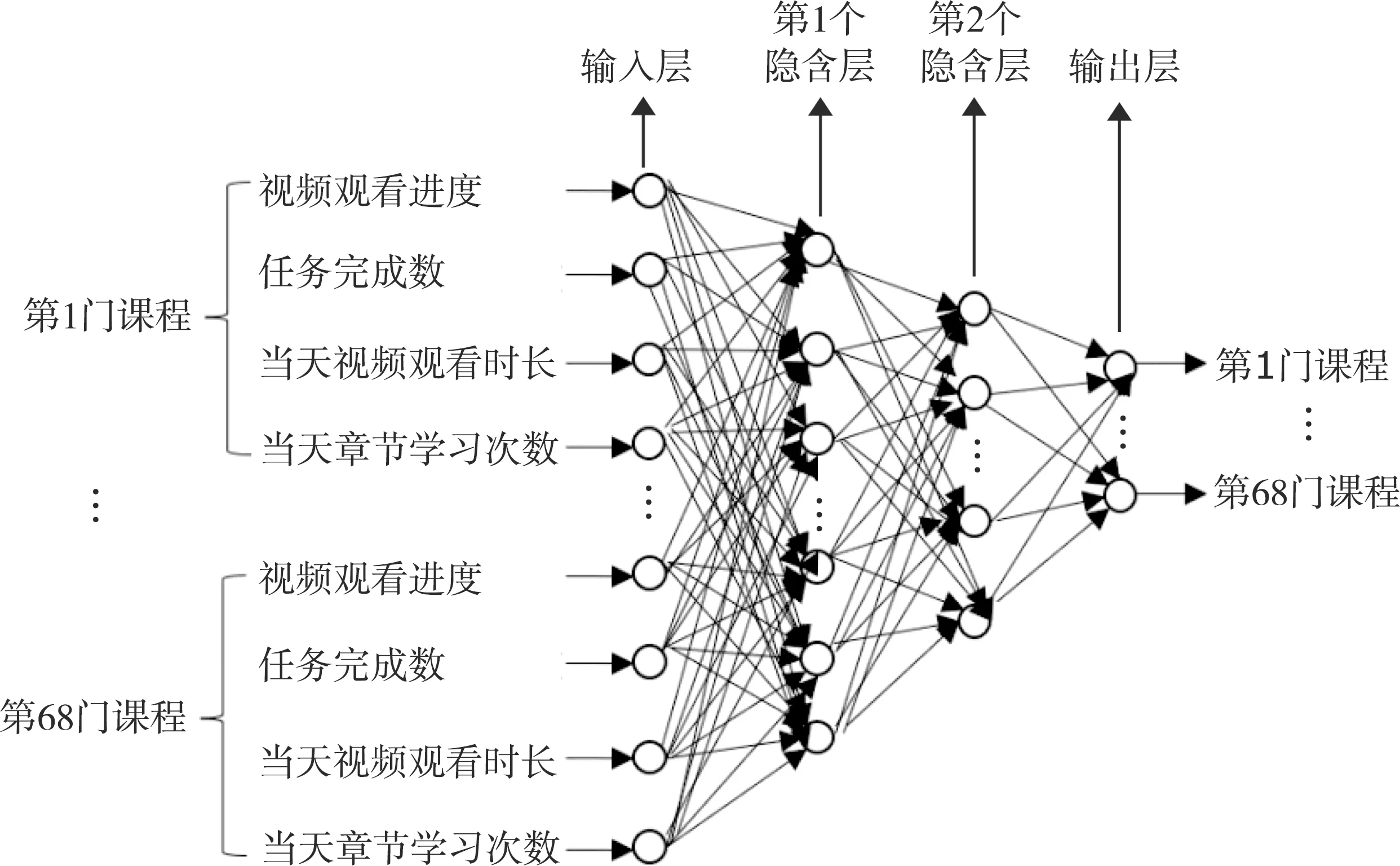
图1 BP预测模型结构

(1) 前向传播。采用ReLU激活函数，如式(2)所示：

f(x)=max(0,x)

(2)

第1个隐含层的前向传播函数如式(3)所示：

H1=Xω1+B1

(3)

式中：H1—— 第1个隐含层的输入矩阵；

X—— 预处理后的课程特征值矩阵；

ω1—— 输入层与第1个隐含层间的权值矩阵；

B1—— 输入层与第1个隐含层间的阈值矩阵。

第2个隐含层和输出层的前向传播函数如式(4)所示：

Hi=ReLU(ωiHi-1+Bi)

(4)

式中i为2或3：当i=2时，H2表示第2个隐含层的输入矩阵，ω2表示第1个隐含层与第2个隐含层间的权值矩阵，B2表示第1个隐含层与第2个隐含层间的阈值矩阵；当i=3时，H3表示输出层的输入矩阵，ω3表示第2个隐含层与输出层间的权值矩阵，B3表示第2个隐含层与输出层间的阈值矩阵。

(2) 反向传播。目前，很多深度学习框架(如PyTorch和Tensorflow等)都自带求导功能[10]。本次研究使用自适应学习速率SGD优化算法对损失函数进行迭代优化。学习率α的取值为0～1。根据多次调试，确定α=0.01。但是，固定的学习率会影响BP神经网络的收敛速度，使其陷入局部震荡，影响模型预测精度。因此，在BP神经网络模型中引入动量因子，不仅能够加快收敛速度，而且能够保证算法始终向着收敛的方向进行。BP神经网络模型如式(5)所示：

(5)

式中：Δx(k) —— 第k次迭代时，网络模型各层权值和阈值的修正量；

x(k) —— 第k次迭代时，网络模型各层的权值和阈值；

α—— 学习率，α=0.01；

η—— 动量因子，取值范围为0～1，经过多次实验确定其最佳值为0.9；

E(k) —— 均方误差。

其中，均方误差E(k)如式(6)所示：

(6)

式中：n—— 样本数量；

xi—— 第i个个体的预测值；

yi—— 第i个个体的实际值。

1.2 BP模型的缺陷

在BP模型中通过调整权值和阈值使预测误差缩小至预定值，这是一个不断迭代训练的过程。训练结束后，使用测试样本对模型进行测试，以判断模型的准确率。将BP模型的权值和阈值存储于N维向量C中，其中N为BP模型中权值和阈值的总数。每次运行BP模型都要在向量C中随机选取数值作为初始权值和阈值，这会影响模型的预测速度。而且，网络对初始权值非常敏感，取值不当容易导致模型迟迟不能收敛至全局最优，因此，在BP模型中引入遗传算法，基于“优胜劣汰”的进化论，全局寻求最优权值和阈值，以提高预测的精度和速度。

2 遗传算法对模型初始参数的优化

遗传算法是计算数学中用于找出最优解的搜索算法，是进化算法的一种，包括自然选择、杂交和变异等[11]。具体步骤如下：

(1) 参数初始化。对种群进行初始化，设最大迭代次数为600次，种群规模为100个。

(2) 个体编码。将每个个体编码成实数串，使每个个体都包含模型各层的权值和阈值。

(3) 确定适应度函数。将适应度函数设为实际输出与预测输出间均方误差的倒数，误差越小，个体适应度越高，其关系如式(7)所示：

(7)

式中：f(j) —— 适应度函数；

m—— 种群规模，m=100；

zj—— 第j个神经元节点的实际值，即训练标签；

oj—— 第j个神经元节点的预测值；

γ—— 调节系数，取值为0～1。

(4) 选择运算。选出适应度最大的个体，对其进行解码之后得到模型的初始权值和阈值。如果该初始权值和阈值能够让模型得到最优解，则保存该初始权值和阈值，停止计算；如果不能，则通过遗传算法中的轮盘赌选择算子，适应度越大的个体被选择的概率越大，如式(8)所示：

(8)

式中：Pr(j) —— 第j个神经元节点的选择概率。

(5) 交叉变异运算。将选择出来的个体随机进行两两搭配放在交配池里，按照交叉概率(Pc)进行单点交叉，生成下一代个体，形成新的种群，而没有参与交配的个体则作为老个体加入到新种群中。新种群中的个体按照变异概率(Pm)发生单点突变，即个体中的单个基因进行变异，生成第3代个体。

标准遗传算法采用的是固定的Pc和Pm，Pc为0.90～0.97，Pm为0.001～0.005。Pc取值过大易变为随机算法，失去交叉的意义；Pc取值过小会影响收敛速度。因此，采用自适应方法，根据个体和种群的适应度确定Pc和Pm。当个体适应度小于种群平均适应度时，Pc达到最大值Pmax=0.97，此时最有可能变异。个体的适应度越大，Pc越小，优秀的个体就越能得到保留。Pc的计算公式如式(9)所示：

(9)

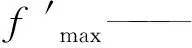
favg—— 种群平均适应度；

fmax—— 种群适应度最大值；

Pmin——Pc的最小值，Pmin=0.90。

(6) 交叉变异后产生的新种群进入步骤(4)，直到找到适应度最大的个体(即得出最优权值和阈值)方可结束运算。

3 实验设计

AGA_BP模型在PyCharm环境下通过Python语言实现，采用PyTorch深度学习框架。

预测模型的评价指标有准确率、均方误差、F1分数、AUC、召回率等。本次研究选取准确率、均方误差和F1分数等3个指标，对BP、GA_BP和AGA_BP模型进行对比分析。由BP、GA_BP和AGA_BP模型准确率的对比结果(见图2)可知，AGA_BP模型的准确率最高为89%，GA_BP模型的准确率最高为81%，BP模型的准确率最高仅为60%，AGA_BP模型的准确率最高，且其收敛速度最快。

由BP、GA_BP和AGA_BP模型均方误差的对比结果(见表2)可知，GA_BP模型的均方误差平均值比BP模型减少了28.72%，AGA_BP模型的均方误差平均值比GA_BP模型减少了27.61%。由BP、GA_BP和AGA_BP模型F1分数的对比结果(见表3)可知，AGA_BP模型的F1分数明显高于BP和GA_BP模型。

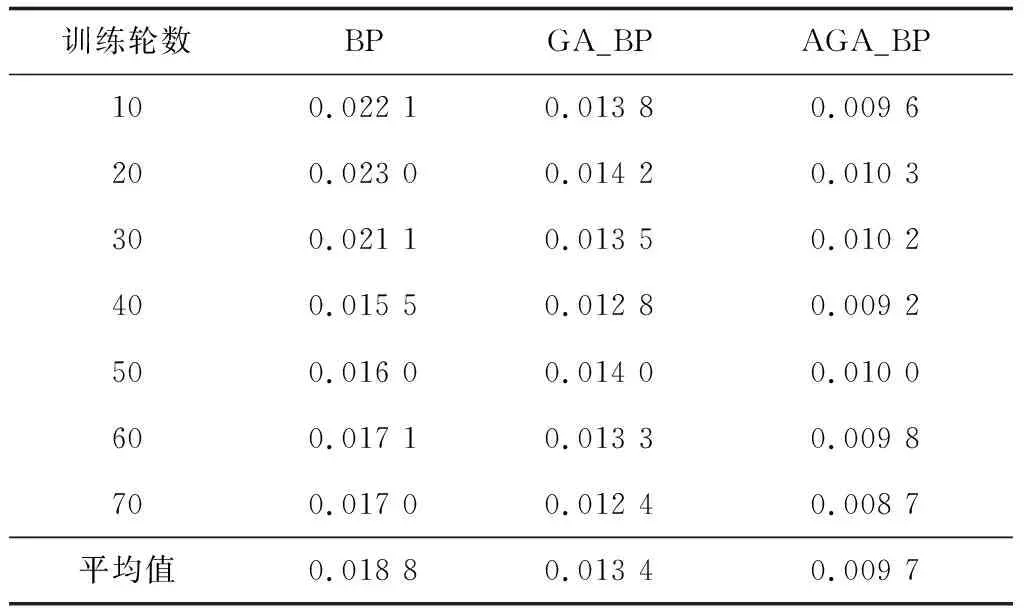
表2 BP、GA_BP和AGA_BP模型均方误差的对比

表3 BP、GA_BP和AGA_BP模型F1分数的对比

4 结 语

通过学习记录分析学习者的学习风格，预测学习者在网络教学平台中的课程偏好，是平台向学习者推荐学习资源的前提，也是帮助学习者实现自适应学习的基础。为此，构建一个具有双隐含层的AGA_BP偏好课程预测模型。与典型的BP和GA_BP 模型相比，AGA_BP模型具有更高的准确率和F1分数，以及更快的收敛速度。今后的研究中，可以在AGA_BP模型的基础上结合CB学习算法[12]的最近邻方法，根据偏好课程的关键字、难易程度等特征，推荐平台中相似度最高的多个课程给学习者，使其获得需要的学习资源。