基于区间二型模糊集的多属性三支决策

王宁

（北京邮电大学理学院，北京 100876）

0 引言

1982 年，波兰学者PAWLAK[1]提出了粗糙集理论，为处理不确定性提供了一个有效的工具。为了完善粗糙集理论，YAO[2]提出了决策理论粗糙集的概念。基于决策理论粗糙集，YAO[2]进一步提出了三支决策的理论。该理论将决策论域划分为三个互不相交的域，并给出了对应的解释。即用接受，拒绝和不做承诺三个决策行动来解释粗糙集的三个域。目前，三支决策已经成功应用到很多领域并取得了很好的结果[3]。

目前，很多三支决策模型都是基于一型模糊集并取得了很好的结果，但随着决策环境不断地变复杂，一型模糊集已经不能满足决策的需求。二型模糊集作为一型模糊集的推广[4-6]，能更好地描述不确定信息。故Xiao 等[7]提出了基于二型模糊集的三支决策。考虑到决策者的行动可能会受到不同风险态度的影响，Wang 等[8]提出了一个区间二型模糊环境下基于后悔理论的三支决策模型[7]。在实际的决策问题中，往往涉及多个属性而不是单一的属性，所以多属性三支决策受到了很多学者的关注。区间二型模糊集在表达和计算上更加的简洁，因此我们将多属性三支决策推广到区间二型模糊集的环境下，来提高模型处理不确定信息的能力。

1 预备知识

1.1 区间二型模糊集

定义1 假设U 是一个论域，˜A 是一个二型模糊集可以表示为：

1.2 决策理论粗糙集和三支决策

由决策理论粗糙集的定义可知，一个模糊概念的上下近似可以通过条件概率和阈值来确定。在决策理论粗糙集中通常包含两个状态和三个行动，分别记作Ω={C，┒C}，D={aP，aB，aN}。C 和┒C 分别表示对象属于和不属于C。aP表示对象x∈pos（C），即接受决策；aN表示对象x∈neg（C），即拒绝决策；aB表示对象x∈bn（C），即拒绝决策；aB表示对象x∈bn(C)，即延迟决策。每个行动的损失函数如表1 所示，其中λPP，λBP，λNP分别表示对象x 属于状态C 时执行行动aP，aB，aN所产生的损失，λPN，λBN，λNN分别表示对象x 不属于状态C 时执行行动aP，aB，aN所产生的损失。假设P（C│[x]）是对象属于[x]的情况下属于C 的概率，然后通过一对阈值0≤β≤α≤1，可以得到如下的决策规则：

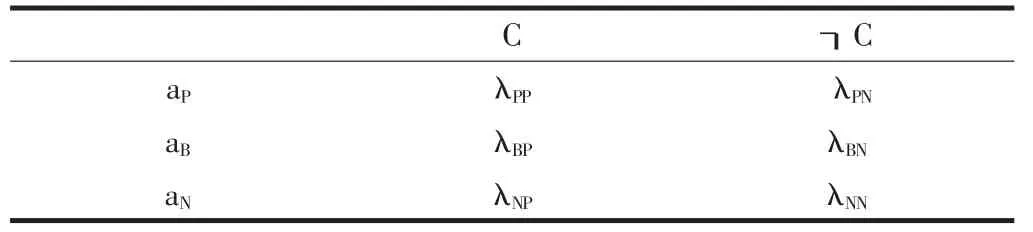
表1 损失函数的矩阵

接受：pos（C）={xi∈U│P（C│[x]）≥α}，

不做承诺：bn（C）={xi∈U│β＜P（C│[x]）＜α}，

拒绝：neg（C）={xi∈U│P（C│[x]）≤β}。

根据贝叶斯决策理论和最小风险原则，我们可以用式（4）至式（6）计算出阈值参数α，β，γ，其中0≤β≤γ≤α≤1：

2 基于区间二型模糊集的多属性三支决策

当决策环境更加复杂时，使用一型模糊集有时不能很好的表达决策对象的评价信息。区间二型模糊集作为一型模糊集的拓展，在表达不确定信息上优于一型模糊集，所以我们提出了一个区间二型模糊环境下的多属性三支决策模型。

虽然区间二型模糊集在表达不确定信息上比一型模糊集更有优势，但在表达形式和计算上会更加的复杂。当得到这些模糊评价信息时，为了便于比较和计算，我们首先要对这些区间二型模糊信息进行处理，将区间二型模糊信息转化为数值的形式并得到一个数值的信息表。因此我们需要提出一个函数将区间二型模糊信息转换为数值。

通过定义2 提出的函数，我们可以将所有的区间二型模糊信息转化为数值，下文将用一个案例来说明该定义的计算过程。

一所学校需要对一个学生进行评估，假设V={1，2，…，10}，班主任对该学生的评价为˜A =[（5，7，8，9；1，0.9），（6，7，7，8；0.8，0.8）]，其中˜A 是V 上的一个区间二型模糊集。 假设V={1，2，…，10}，˜A =[（5，7，8，9；1，0.9），（6，7，7，8；0.8，0.8）] 是V 上的一个区间二型模糊集。利用函数T 我们可以计算出：

相当于班主任对这个学生的评价可以近似为0.635。

处理完区间二型模糊信息，则需要考虑三支决策的两个关键因素：条件概率和阈值。首先，考虑到不同的属性的重要程度可能是不同的，如果将各个属性的权重设为一样的，那么得到的决策结果可能会有偏差，因此我们将权重加入条件概率的公式之中，并给出了加权的条件概率的定义。

利用条件概率的公式计算出条件概率后，则需要考虑三支决策的另一个关键因素：阈值参数。阈值参数可以通过贝叶斯风险决策理论和最小风险原则计算得到，为了减小模型的计算量，本文的阈值参数是根据经验直接给出的。给定一对阈值α 和β（0≤β≤α≤1），如下的三支决策规则被给出：

接受：pos（C）={xi∈U│P（C│xi）≥α}，

不做承诺：bn（C）={xi∈U│β＜P（C│xi）＜α}，

拒绝：neg（C）={xi∈U│P（C│xi）≤β}。

通过以上讨论，我们建立了一个基于区间二型模糊集的多属性三支决策模型。

3 算例分析

本节中笔者将通过一个数值的例子来验证所提出的基于区间二型模糊集的多属性三支决策的有效性和合理性。

假设一个科技公司需要招聘后端开发工程师，一共有3 名求职者U={x1，x2，x3}通过了笔试的筛选进入了面试的流程，面试官将通过专业知识、实践经验和综合分析能力三个方面对应聘者进行评估。这三个属性的权重分别为（0.3，0.3，0.4），基本集V={1，2，…，10}，状态集Ω={C，┒C}，其中状态C 表示通过面试。得到的信息如表2 所示。

表2 一个关于面试的区间二型模糊信息表

首先，我们利用定义2 中的函数T 对得到的区间二型模糊信息进行处理，将所有的区间二型模糊信息转化为数值，得到的信息如表3 所示。

表3 一个关于面试的数值信息

然后，通过定义3 给出的条件概率的计算公式，得到各个求职者的条件概率如下：

P（C│x1）=0.601，

P（C│x2）=0.747，

P（C│x3）=0.450。

根据以往的经验，我们设阈值α=0.7 和β=0.4，根据推导出的三支决策规则可以得到：

接受：pos（C）={xi∈U│P（C│xi）≥0.7}={x2}，

不做承诺：bn（C）={xi∈U│0.4＜P（C│xi）＜0.7}={x1，x3}，

拒绝：neg（C）={xi∈U│P（C│xi）≤0.4}=ø。

通过上面的决策结果，我们可以知道求职者x2通过了面试，得到了该科技公司的工作；针对求职者x1和x3，该科技公司没有给出正面的评价，需要增加面试的次数再进一步考虑是否录用，决策的结果如图1 所示。

图1 决策结果

4 结语

本文给出了一个基于区间二型模糊集的多属性三支决策模型。与基于一型模糊集的三支决策模型相比，该模型在表达模糊信息上更有优势。且能够处理更多的模糊信息和决策问题。条件概率和阈值是三支决策的两个关键因素，本文给出了条件概率的计算公式，但阈值是根据经验直接给定的。为了完善我们的模型，在未来将研究区间二型模糊环境下阈值的确定方法。另外，随着决策环境不断地变复杂，决策过程中往往涉及多个决策者，所以我们还将研究基于区间二型模糊集的多属性群三支决策。