基于高斯金字塔与新粒子群的印刷电路板装配模板匹配算法

闫 河，李晓玲，谢 敏，赵其峰，刘伦宇

(1.重庆理工大学 计算机科学与工程学院，重庆 400054；2.重庆理工大学 两江人工智能学院，重庆 401135)

0 引言

随着电子技术的进步，印刷电路板装配(Printed Circuit Board Assembly, PCBA)趋于微型化、密集化，导致元器件的装配定位、尺寸测量和分割等工作非常困难，其中元器件目标区域检测是定位、测量和分割的首要问题。目标区域检测的准确性直接影响后续定位、测量和分割精度；准确性低容易出现错检、漏检情况，导致定位、测量和分割结果偏差较大。提高目标定位、测量和分割精度及计算实时性，是PCBA产线非常重要的任务。

机器视觉检测系统通常采用模板匹配方法检测目标区。模板匹配方法是在源图像中找到与模板图像相关性最大的位置，因此可以根据相关性建立一个全局优化问题，采用优化技术找到最优匹配位置。近年来，有许多学者将粒子群优化(Particle Swarm Optimization, PSO)算法应用于模板匹配领域[1-2]。TAVARES等[3]采用PSO算法搜寻最佳匹配位置，利用PSO算法概率搜索特性减少匹配次数，降低相关性计算量，从而缩短匹配时间；MAOGUO等[4]考虑到PSO算法参数少、收敛速度较快，将其用于高阶图匹配。然而，经典PSO算法容易过早收敛而陷入局部解[5-6]，匹配准确性不高。因此有学者对影响粒子群优化的参数、位置和速度进行改进。SHI等[7]提出线性调整权重的PSO算法，平衡了算法搜索能力；姜建国等[8]采用自适应学习因子在不同搜索阶段自动调整合适的学习因子，使粒子能更好地学习靠近最优解；冯浩等[9]通过引入活力因子提出一种名为自适应变异粒子群优化算法(Adaptive Mutation Particle Swarm Optimization, AMPSO)算法的改进PSO算法，其能有效激发失活粒子跳出局部最优解，从而提升算法的全局寻优能力；杨延西等[10]引入混沌映射，提出混沌粒子群优化(Chaos Particle Swarm Optimization, CPSO)算法，增加了粒子群的多样性，使算法全局寻优能力得到进一步提升。

虽然改进的PSO算法性能都有提升，但是匹配的准确性和实时性仍然较低。考虑到图像高斯金字塔变换(Gaussian Pyramid Transformation, GPT)匹配算法[11]采用遍历匹配方法保证了匹配的准确性，但是耗时较长，PSO算法准确性较低，但运算时间较短，而实际应用中对PCBA目标区域检测的准确性和实时性都有较高要求，可以结合两种算法进行互补。因此，本文提出一种GPT与新PSO算法结合的PCBA模板匹配算法，该算法结合GPT与新PSO算法，利用图像GPT匹配算法的遍历匹配方法提高匹配准确性，利用新PSO算法改变搜索策略进一步缩短匹配时间。实验表明，本文算法能较好地满足PCBA视觉检测的要求。

1 标准粒子群优化算法

PSO算法是群体智能优化算法中的一种，是通过模拟鸟群捕食的信息传递行为提出的优化算法[12]，该算法具有群体智能的局部和全局搜索能力且参数较少。

假设在一个K维空间中，粒子数为m，根据式(1)和式(2)初始化粒子群的位置和移动速度：

Xi=LX×rand；

(1)

Vi=LV×rand。

(2)

式中：LX和LV分别为粒子群的位置和移动速度的边界值；rand为均匀分布的随机数。

进行到t次迭代时，第i个粒子在空间中的位置表示为Xi(t)=(xi1,xi2,…,xiK)，飞行速度表示为Vi(t)=(vi1,vi2,…,viK),适应度值表示为Pi(t)=(pi1,pi2,…,piK)，其中i=1,2,3,…,m。根据适应度值选择粒子个体中的最大值作为最优解Pbest(t)，将群体中搜索到的最优解记为gbest(t)，根据如下速度和位置动态调整公式对粒子进行更新：

Vi(t+1)=ωVi+c1r1(Pbest(t)-Xi(t))

+c2r2(gbest(t)-Xi(t))；

(3)

Xi(t+1)=Xi(t)+Vi(t+1)；

(4)

Pbest(t)=max{Pi(j)|1≤j≤t}；

(5)

gbest(t)=max{Pbest(j)|1≤j≤t}。

(6)

式中：ω为惯性权重；t和T分别为第t次迭代和最大迭代次数；c1为个体学习因子，c2为群体学习因子，一般取值为2；r1和r2均为属于[0,1]范围内互不干扰的随机数。

2 高斯金字塔变换与新粒子群优化算法结合的匹配算法

2.1 新粒子群优化算法

虽然PSO算法参数少、简单易用，但是容易陷入局部最优，且粒子寻优能力与参数变化密切相关[13]。因此，本文对标准参数变化提出以下改进，从而提出一种新PSO算法。

2.1.1 惯性权重

惯性权重是粒子移动的重要影响因子之一。对于PSO算法，惯性权重较大时全局寻优能力强，惯性权重较小时局部寻优能力强。SHI等[7]对惯性权重采用线性递减的方式调整，虽然有效提高了算法性能，但是算法迭代前期惯性权重值递减速度较快，容易使算法陷入局部最优。针对该问题，采用黄洋等[14]提出的倒Sigmod函数衰减方式进行调整，使惯性权值在前期和后期缓慢变化。具体公式为

(7)

式中：ωmax和ωmin为惯性权重的最大值和最小值；a和b表示非线性调整系数，a=3.4，b=0.07；t为迭代次数。这种变换方法可以让惯性权值在算法迭代前期和后期能用较长时间取得较大值和较小值来平衡全局和局部搜索能力，但是粒子群依赖个体竞争与群体协作寻优，仅调整惯性权值不能更好地发挥搜索性能。

2.1.2 自适应学习因子

学习因子c1，c2的变化分别影响个体和群体粒子向最优解靠近。迭代前期较大概率依赖粒子个体的移动经验进行全局搜索，迭代后期主要依赖群体的移动经验进行局部搜索。传统PSO算法采用固定的学习因子，无法在不同阶段更好地引导个体和群体向最优解靠近。因此根据PSO算法的特性，PSO算法在迭代前期学习因子c1取较大值、c2取较小值能增强全局搜索能力，后期c1取较小值、c2取较大值能增强局部搜索能力。为了在不同阶段更好地发挥全局和局部搜索能力，采用自适应的学习因子，关系如下：

(8)

(9)

2.1.3 随机动量因子

虽然对参数影响因子进行动态调整能有效提高寻优能力，但是无法完全避免过早收敛陷入局部解。方差能够表现数据离散程度的特性，判别粒子是否收敛陷入局部解，如式(10)所示；为了使粒子扩大搜索范围并跳出局部解，引入随机动量因子λ进行扰动，如式(11)所示。

(10)

Xi(t)=λLX。

(11)

2.2 高斯金字塔变换与新粒子群优化结合算法

图像匹配通常采用由粗到精的方式来保证匹配的准确性，将图像GPT匹配算法由粗到精的分层匹配思想和新PSO算法结合可以进一步提高匹配效果。在不同图像层采用由粗到精的匹配方式能够弥补新PSO算法准确性不高的问题，而新PSO算法可以替代图像GPT的遍历式匹配，进一步加快计算速度，两种算法相辅相成，可以达到较好的效果。本文算法首先对待匹配图像和模板子图进行高斯金字塔变换，在变换后的待匹配图像顶层子图中采用新PSO算法搜索粗匹配区域，在后续层的邻域范围内进行逐像素精匹配，其中GPT通过图像与高斯函数多次卷积后获得图像的低通滤波，然后进行二次下采样产生不同尺寸的图像塔，详细构造过程参见文献[15]。本文算法具体步骤如下：

步骤1设置金字塔层数为L，分别对待匹配图像和模板图像进行高斯金字塔变换。

步骤2在待匹配图像变换后的L层子图中采用新PSO算法搜索粗匹配区域，新PSO算法搜索的详细过程如下：

(1)初始化PSO算法参数，即种群个数m、空间维度K、迭代次数T。

(2)根据式(1)和式(2)初始化粒子群的位置和移动速度，将NCC系数[16]作为适应度值Pi，然后根据式(5)和式(6)找出个体和群体的初始最优值。

(3)根据式(3)～式(11)更新粒子的移动速度、位置、个体最优值和群体最优值。

(4)若t=T，则算法运行结束，将群体最优值反变换传入L-1层;否则执行(3)。

步骤3设置邻域大小为n×n，在邻域范围内将相同层的模板子图与待匹配子图逐像素匹配，找到最佳匹配位置。

步骤4若L=0，则算法结束，输出匹配区域；否则执行步骤3。

3 实验结果及分析

为了验证本文算法(对比试验中简称Our Proposed)的有效性，将上述方法与PSO算法[7]、AMPSO算法[9]、CPSO算法[10]、GPT算法[11]进行比较。实验环境为：Intel(R)Core(TM)i5=8300H CPU、8 G内存、Windows 10操作系统、MATLAB R2018a。

3.1 运行时间比较

图1所示为测试图像，其中：图1a为待匹配图像，尺寸为484×800；图1b为模板图像，尺寸为95×95。保持图1b左上角坐标不变，按照10个像素递增另取4种大小分别为105×105，115×115，125×125，135×135的模板图像，在每种尺寸下分别进行20次实验来比较5种算法的平均运行时间。本文算法参数设置为粒子数m=80、最大迭代次数T=80，L=4，K=2，n=5，实验结果如表1所示。

表1 运行时间比较 s

由表1可见，相同尺寸下，本文算法的运行时间明显低于其他算法。随着尺寸的增大，PSO和AMPSO算法时间的增幅在0.17 s～0.28 s内，CPSO算法时间的增幅在0.37 s～0.55 s内，GPT算法时间的增幅在0.1 s～0.38 s内，本文算法时间的增幅在0 s～0.01 s内，验证了本文算法的实时性。

3.2 匹配准确性比较

匹配准确性通常采用模板图像和待匹配图像的重叠率[17]衡量。分别采用3.1节的5种算法在测试图像的5种尺寸下进行50次试验，比较匹配的准确性。实验结果如图2、图3和表2所示。

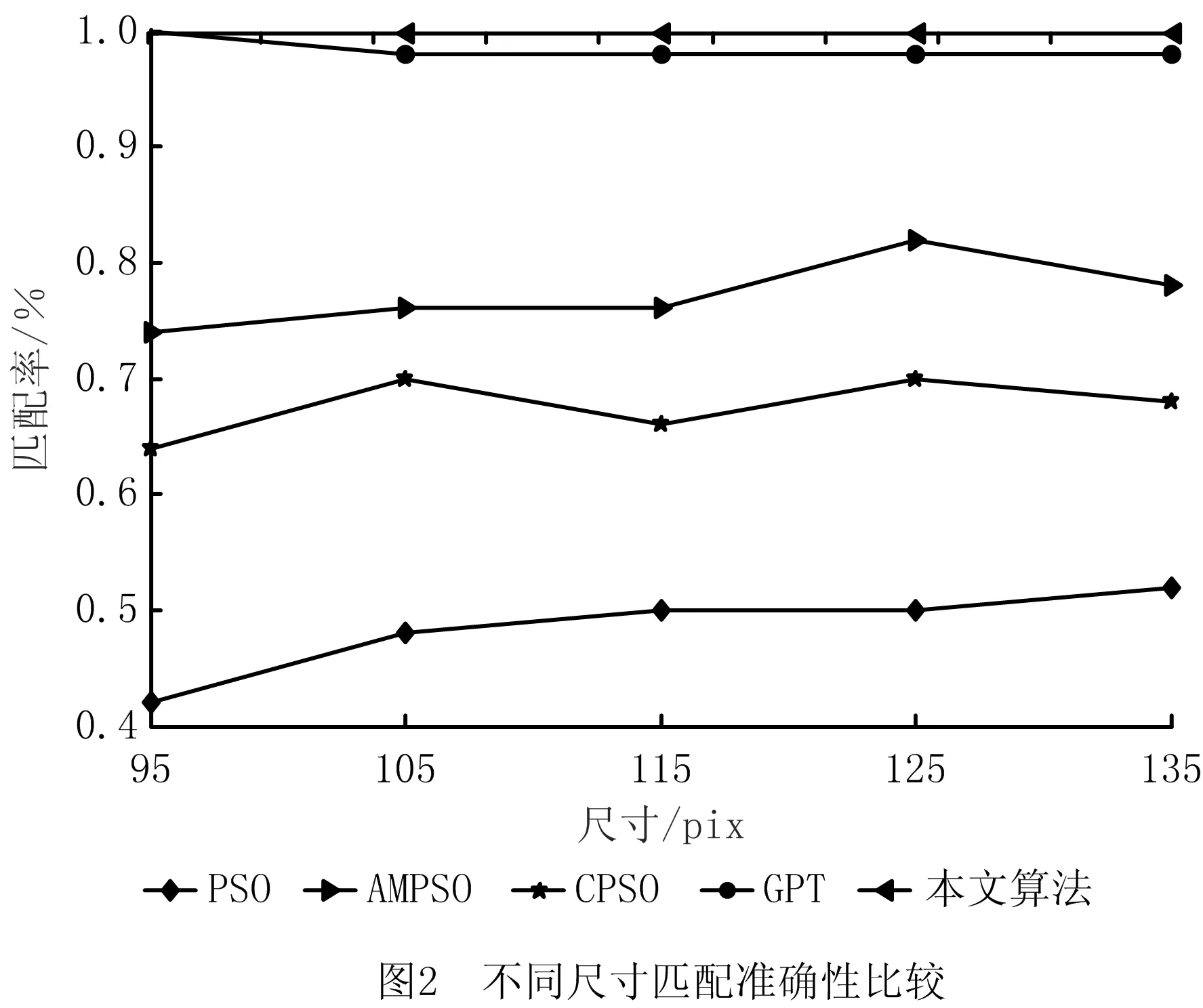
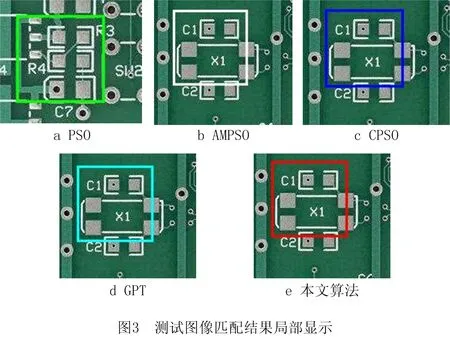
表2 准确性比较

由图2可见，本文算法的准确性明显高于其他4种算法。表2所示为不同算法的准确性比较，可见在无噪声干扰下，AMPSO算法和CPSO算法的匹配率比传统PSO算法提升了28.8%和19.2%，本文算法比AMPSO算法、CPSO算法、GPT算法提升了22.8%，32.4%，1.6%，验证了本文算法在保证实时性的情况下，比其他算法的匹配准确性更高。

3.3 鲁棒性比较

为了验证本文算法在保证匹配准确性和实时性的情况下还具有鲁棒性，在3.1节5种测试图像中加入方差为0.01～0.1的高斯白噪声，分别对5种算法在不同尺寸下进行30次实验，比较每种尺寸加入10级噪声后的平均匹配率，实验结果如图4所示。对比实验结果可知，在添加不同程度的高斯白噪声下，本文算法的平均匹配准确率为99.58%，明显高于其他4种算法，表明该方法同时具有鲁棒性。

4 结束语

为提高PCBA中目标区域检测的准确性和实时性，提出GPT与新PSO算法结合的PCBA模板匹配算法，不仅可以提高PCBA检测的准确性，还能加快运行速度、保证实时性，同时具有较好的鲁棒性。本文提出一种新的PSO算法，该算法采用倒Sigmod函数调整粒子群惯性权值，分别构建个体和群体的自适应学习因子模型，同时提出粒子是否陷入局部解的自适应判据并对粒子采用随机动量因子进行调整，然后与高斯金字塔相结合，在不同层采用由粗到精的匹配方式，不但提高了匹配准确性和实时性，而且具有较好的鲁棒性。实验表明，本文算法在计算速度、匹配准确性或鲁棒性的任一方面，均比经典PSO算法、相关改进算法和图像金字塔算法有显著提升，验证了本文算法应用在PCBA目标区域检测中的有效性。考虑到多目标区域检测的情况，后续将对本文算法进行进一步改善，以提升算法性能和适用性，使算法能更好应用于PCBA目标区域检测。