基于三角网格模型的自由曲面自适应测点规划

郭润琪，盛步云+，陆辛成

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.湖北省数字制造重点实验室，湖北 武汉 430070)

0 引言

随着现代制造技术的发展，为追求某些特殊功能需求或外观形态，自由曲面越来越广泛地应用于航空航天、汽车、模具和造船等领域，数字化检测已经成为保障自由曲面加工精度的重要操作之一。同时，随着计算机图形学的发展，用于描述三角网格模型的STL(stereolithography)文件格式成为计算机辅助设计/计算机辅助制造(Computer Aided Design/Computer Aided Manufacturing, CAD/CAM)系统的一类标准接口文件格式，其不但可以满足模型信息在不同软件系统之间高效、及时传输的需求，而且占用的储存空间较少。因此，研究一种面向自由曲面三角网格模型的测点自适应分布算法非常必要。

来新民等[1]、何改云等[2]和张安社等[3]根据曲率推导测点基于曲率分布的函数，通过曲率控制测点疏密来实现测点的自适应分布；SUN等[4]借助加工误差模型优化了根据Hammersley序列分布的测点，以保证在偏差可能性高的区域分布更多测点。这类方法主要基于曲率规划测点，根据曲率大小确定测点的疏密度，使测点能够较好地描述曲面，然而该方法没有分析曲率与测点密度之间的关系，不利于精简测点数量。陈岳坪等[5]和张现东等[6]根据“曲面—曲线—点集—测点集”的策略规划测点，借助几何分解降维的思想将二维曲线的布点方法运用到三维曲面，实现了测点自适应分布，然而该方法需要逐一确定截面间距和测点分布的步长，加大了布点的工作量。YU等[7]和喻明让等[8]采用初始测点重构曲面，然后将重构曲面与原始曲面比较，在误差最大处增加测点，如此循环迭代直至满足条件。这类方法能够保持较高的采样精度，然而所分布的测点大多杂乱，且过多依赖于相应的加工误差模型和曲面拟合算法的精度，方法迭代次数较多。RAMAN等[9]根据平均高斯曲率将曲面分割为多个子曲面,然后在各子曲面的高斯曲率特征值处进行初始布点，并将初始测点重构曲面与原始曲面比较，在偏差较大处增加测点，对初始测点进行优化。这类方法通过划分曲面和减小偏差来实现测点的自适应分布，而且简化了测点坐标的求取过程，然而其对曲面的划分不够细致，无法精简测点数量。大多数曲面自适应采样策略均通过用曲率表征曲面复杂度[10]来分布测点，再根据加工误差或拟合误差优化测点。

综上所述，本文基于自由曲面的三角网格模型，借助曲面分片加工的思想[11-12]将自由曲面划分为测点密度大致相等的若干子曲面，在不同子曲面用其对应的测点密度进行均匀布点，实现测点的自适应分布。首先，制定测点密度判断原则生成测点密度集，进而训练神经网络构建测点密度预测模型，用该模型预测机床加工精度、公差、测量精度既定的自由曲面在不同平均曲率处所对应的测点密度，以精简测点的数量；然后，将自由曲面划分为测点密度大致相等的子曲面，并在各子曲面均匀布点，避免根据曲率不同而迭代计算各测点的分布位置，同时实现了测点的自适应分布；最后，根据拟合误差和公差要求优化曲面整体测点分布，进一步保证采样精度。

1 测点自适应规划算法流程

规划自由曲面测点时，因为其曲率变化范围大且大小不确定，曲面各部分的测点密度不同[12]，所以本文划分自由曲面，使子曲面的测点密度大致相同，可采用均匀布点方式在各子曲面进行局部布点。本文算法流程如图1所示，其中输入为自由曲面三角网格模型(称为输入模型)，输出为自适应规划的测点集(称为输出测点集)。具体步骤如下：

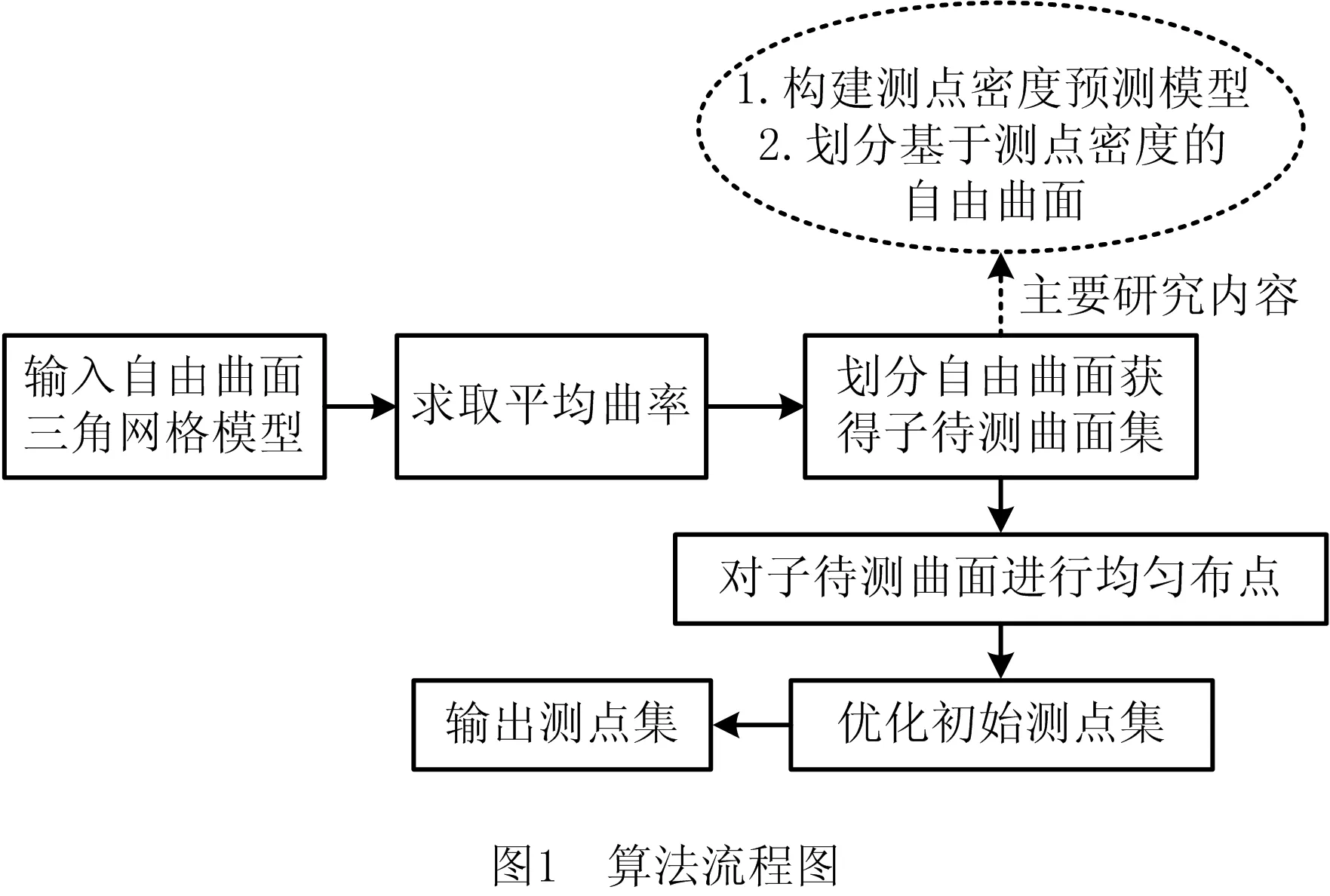
(1)求取平均曲率 采用相关算法求取自由曲面三角网格模型各三角面片顶点处的平均曲率。

(2)划分子曲面 根据测点密度预测模型获取输入模型各处对应的测点密度，将输入模型划分为测点密度大致相等的子曲面集(称为子待测面集)。

(3)分布测点 遍历子待测面集，根据各子待测面对应的测点密度，在子待测面上均匀分布测点，获得初始测点集。

(4)优化初始测点集 拟合初始测点集，比较其与输入模型的误差，在误差大于公差要求处增加测点，获得输出测点集。

本文主要研究构建所划分自由曲面的测点密度预测模型和基于测点密度的自由曲面划分方法，进而实现自由曲面测点自适应分布。

2 测点密度预测模型

待测面的轮廓评定结果受测量误差影响，测点密度是其重要的影响因素，而测点密度主要受机床加工精度、公差、测量精度和曲率影响[13-15]。相同半径球面上的平均曲率相同，本文算法所划分的子曲面的平均曲率在各处也大致相同，而且任何足够小的曲面都可以近似为球面[16]，因此针对球面的测点密度进行研究与分析。测点密度预测模型的输入变量(机床加工精度x1、公差要求x2、测量精度x3、平均曲率x4)和输出变量(测点密度t1)构成一个4输入1输出的非线性函数，难以用传统方法建立精确的数学模型，而且利用单一神经网络构建的测点密度预测模型精度不高，因此本文分别用样本数据训练BP(back propagation)神经网络、径向基函数(Radial Basis Function, RBF)神经网络、广义回归神经网络(General Regression Neural Network, GRNN)，再用遗传算法求解权值组合，使预测误差的平方和最小，即满足式(1)，从而得到组合模型(如图2)，对测点密度进行预测。

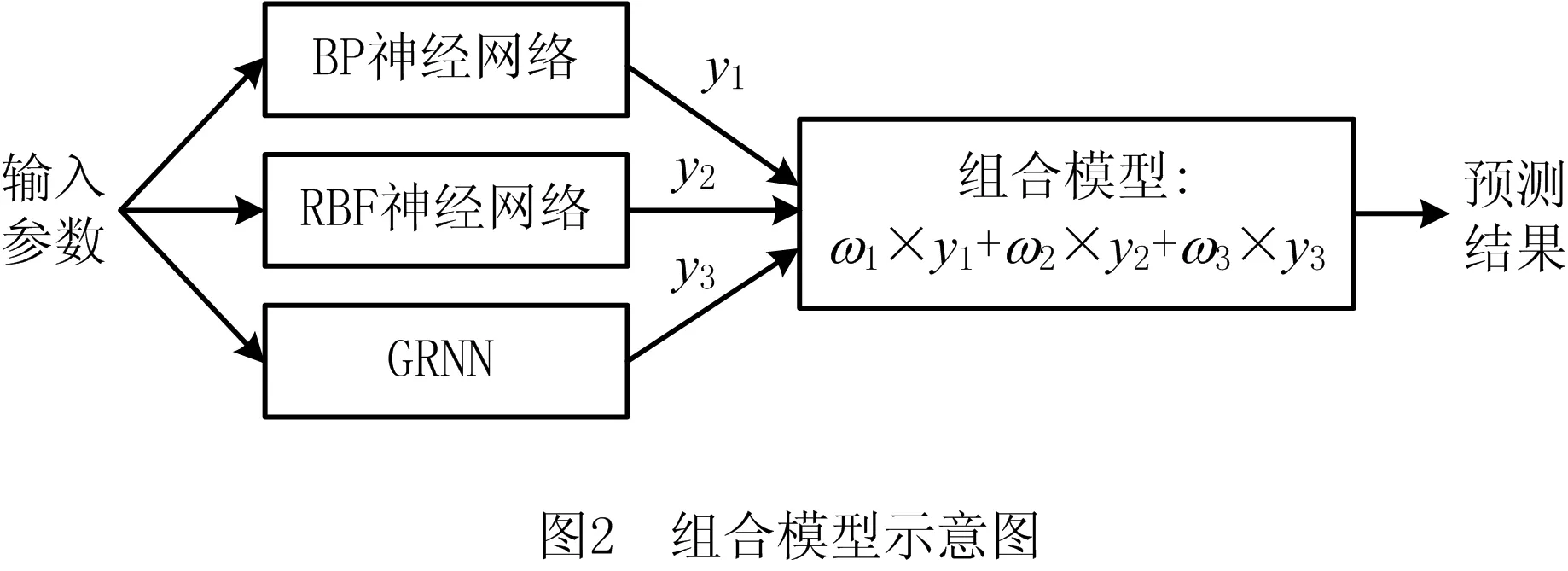
ω1,ω2,ω3>0,ω1+ω2+ω3=1。

(1)

式中：n为预测值的个数；y1i，y2i，y3i分别为BP神经网络、RBF神经网络、GRNN的第i个预测值，y0i为第i个实际值；ω1，ω2，ω3分别为BP神经网络、RBF神经网络、GRNN的权值。

2.1 最佳测点密度判定方法

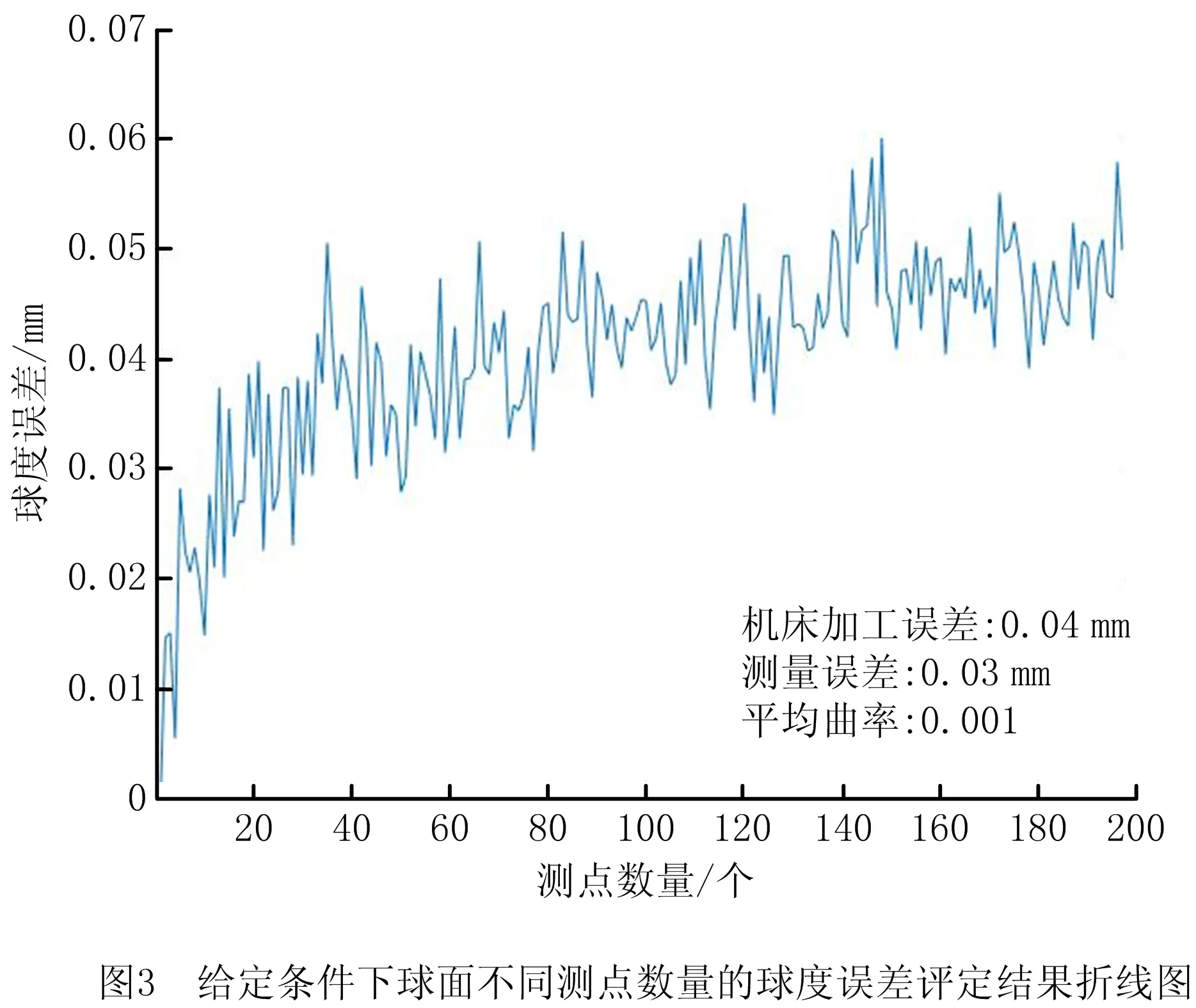
本文根据不同测点数量在球面上采用均匀布点规则采集测点，考虑到实际加工和测量过程中存在误差，将根据给定的机床加工精度和测量精度随机对测点按照球面的径向添加加工误差值和测量误差值，并通过最小包容区域法对不同数量的测点进行球度评定[17]，评定结果如图3所示。从试验结果看,随着测点数量的增加，球度评定结果先呈上升的趋势,上升到某个值后，在其附近上下波动。由此可以推断，随着测点数量的增加，测量数据逐渐逼近加工球面的实际情况，而且其球度评定结果应在某个值附近上下波动。一般情况下，测量误差应不超过设定公差值的1/3～1/10[18]。因此，本文设计的给定条件下的最佳测点密度判定方法为：取给定机床加工精度、公差、测量精度和平均曲率的球面，评定不同测点数量对应的球度误差；根据给定公差范围，设置测点数量右侧球度误差的波动范围小于公差值1/3的条件，选取满足这一条件的测量数量中的最小值，用该最小值除以给定的面积，即为在给定条件下的最佳测点密度。

2.2 训练样本、调优样本和测试样本的构建

分析自由曲面零件的机床加工精度[19]、公差要求[20]、测量精度、平均曲率的主要变化范围，设定样本输入量。根据本文制定的最佳测点密度判定方法获取相应输入条件下的测点密度，即样本输出量。删除部分加工精度、测量精度不适用于相关公差要求的样本组合，共生成5 775组样本数据，部分数据如表1所示。本文采用的样本集较小，为保证调优样本和测试样本的大小，本文选用常用的6∶2∶2的比例划分样本集，从样本中随机选取60%作为训练样本，20%作为调优样本，剩余样本作为测试样本。

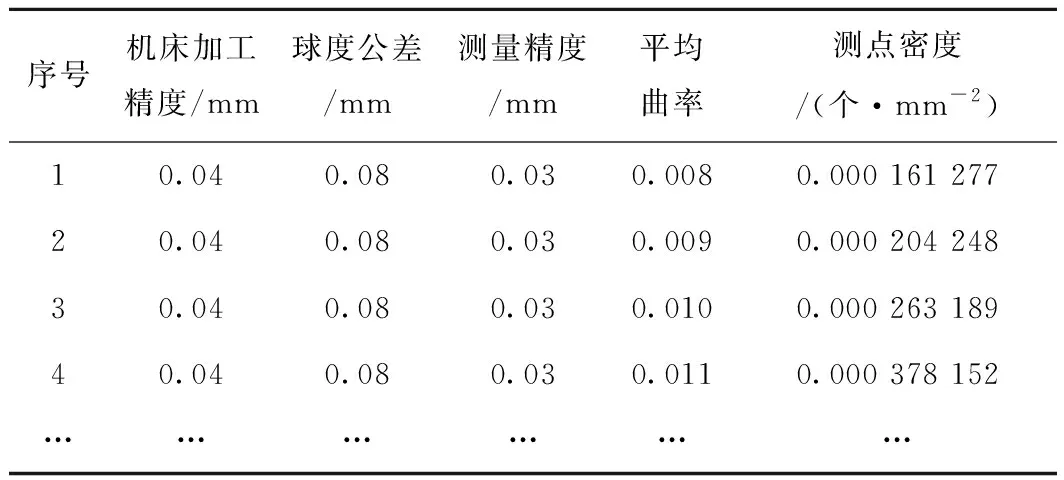
表1 部分样本数据

2.3 基于组合模型的测点数量预测模型的构建

(1)BP神经网络模型的构建

本文基于BP神经网络构建的测点密度预测模型结构为：4-10-1(用经验公式确定隐藏层节点个数)，输入层的4个神经元分别对应加工精度、公差、测量精度、平均曲率，输出层的神经元对应测点密度；采用粒子群优化算法求取使调优样本拟合值与实际值均方差最小的相关参数组合，对BP模型进行优化，优化后的迭代次数为91 277，学习率为0.704 5，目标误差为0.000 470 63；隐含层函数采用logsig，输出层函数采用purelin，训练函数采用traingdx。基于BP神经网络构建的测点密度预测模型的预测结果如图4所示。

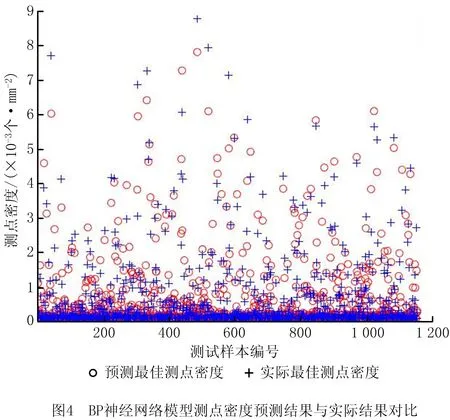
(2)RBF神经网络模型的构建

本文基于RBF神经网络构建的测点密度预测模型的输入层、输出层确定方法同BP神经网络，调用MATLAB神经网络工具确定RBF的拓展速度，本文用粒子群算法优化RBF神经网络的相关参数。RBF的拓展速度为1，此时调优样本的RBF模型拟合值与实际值的均方差最小。基于RBF神经网络构建的测点密度预测模型的预测结果如图5所示。

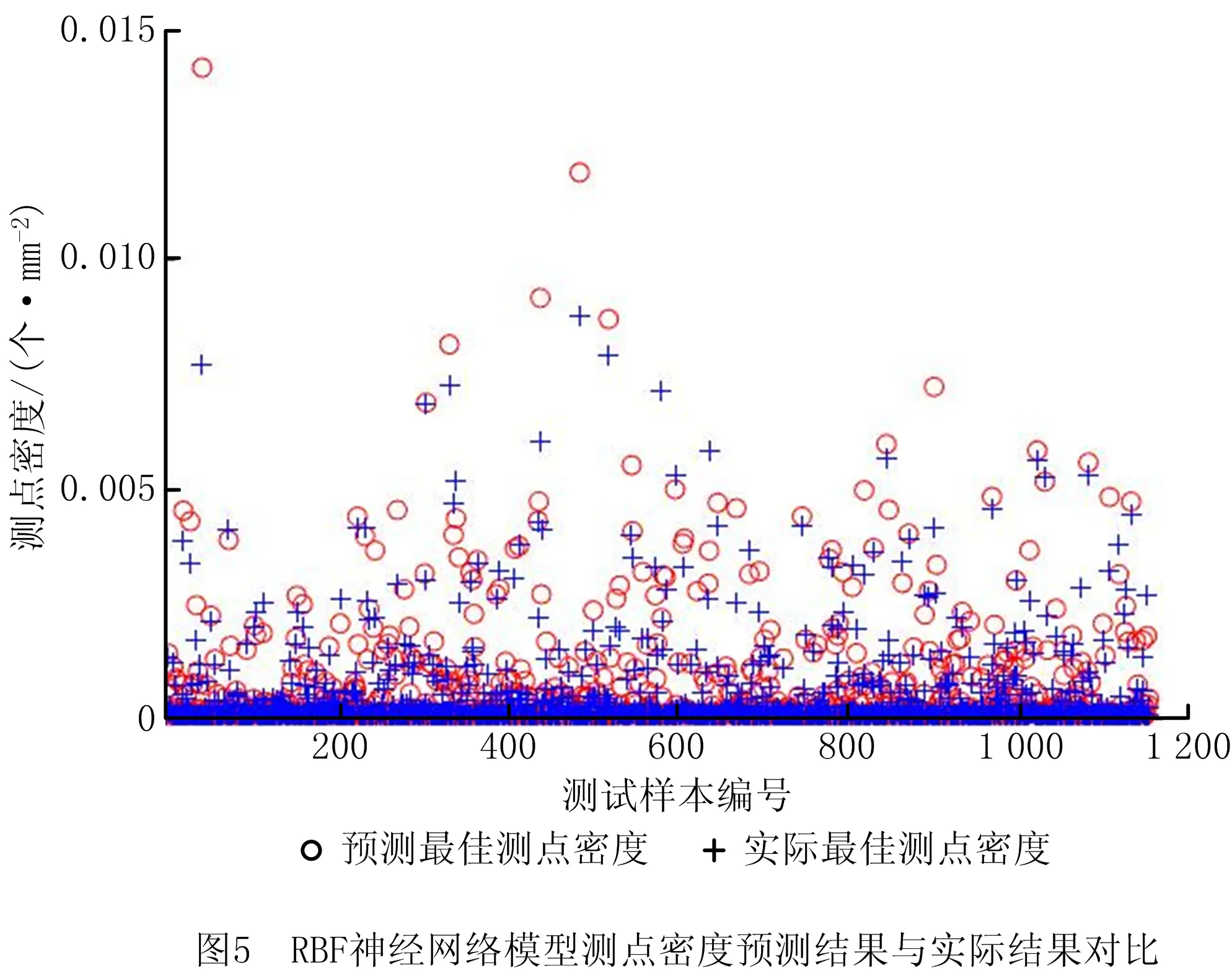
(3)GRNN模型的构建

本文基于GRNN构建的测点密度预测模型的输入层、输出层确定方法同BP神经网络，调用MATLAB神经网络工具确定光滑因子，本文用粒子群算法优化GRNN神经网络的相关参数。光滑因子为0.107 9，此时调优样本的GRNN模型拟合值与实际值的均方差最小。基于GRNN构建的测点密度预测模型的预测结果如图6所示。

(4)组合模型

根据上述3种神经网络模型的预测结果，按照式(1)建立方程组，采用遗传算法求解方程组可得：BP神经网络模型加权系数为0.500 0，RBF神经网络模型的加权系数为0.166 7，GRNN模型的加权系数为0.333 3。按照该加权系数进行组合预测，可得基于组合模型构建的测点密度预测模型的预测结果如图7所示。根据测试样本对各预测模型的评估如表2所示，在4个预测模型中，组合预测模型的均方误差(Mean Square Error, MSE)和平均绝对比例误差(Mean Absolute Percentage Error, MAPE)最小，表明其预测值最接近实际值；组合预测模型的R值最接近1，表明其模型拟合度最高。因此本文采用基于组合模型构建测点密度预测模型。

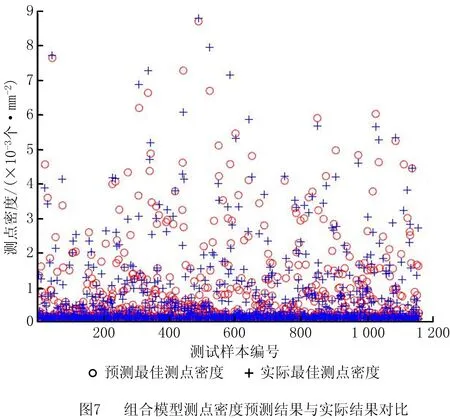
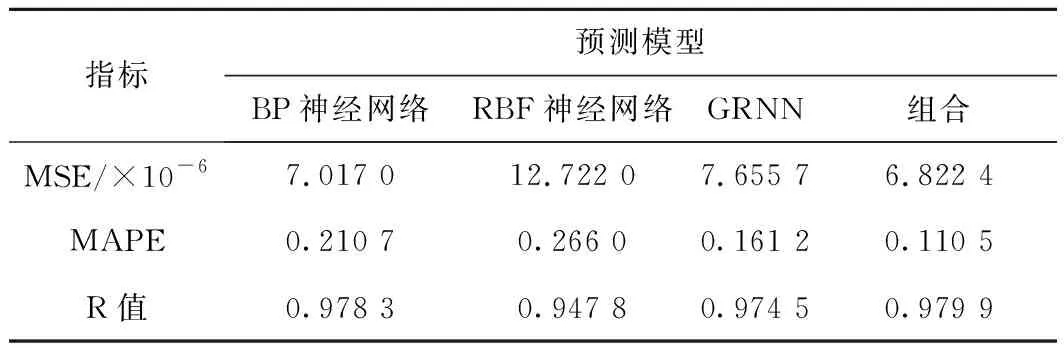
表2 模型性能与精度评估

3 基于测点密度的自由曲面划分

针对机床加工精度、公差、测量精度既定的自由曲面，其测点密度随曲面各处曲率的增加而增大。为实现测点的自适应分布，采用本文构建的测点密度预测模型计算各三角面片所需的测点密度，在聚类算法的基础上，结合区域生长算法，采用二次划分技术基于测点密度划分自由曲面。

3.1 计算三角面片测点密度

给定机床加工精度、公差和测量精度，采用本文构建的测点密度预测模型求取曲面各点处的曲率来预测该点处的测点密度。由于组成自由曲面三角网格模型的三角面片较小，其上各点对应的平均曲率接近，为简化计算，本文用各三角面片顶点平均曲率的算术平均值近似代替该面片上各点对应的平均曲率，即

Hi=(Hi1+Hi2+Hi3)/3。

(2)

式中：Hi为第i个三角面片上各点对应的平均曲率；Hi1，Hi2，Hi3为第i个三角面片上3个顶点对应的平均曲率。

3.2 基于聚类算法的一次划分

在获取各三角面片所需的测点密度后，采用聚类算法将自由曲面模型的三角面片划分为测点密度近似的三角面片集，进行曲面的一次划分，从而减少之后二次划分所需遍历的三角面片数量，提高算法速率。

为保证各面片集的测点密度趋于一致，本文根据给定的阈值，分析以各三角面片为聚类中心的三角面片集的测点密度均值，选取均值最接近其测点密度的三角面片为此时的聚类中心，并从整体三角面片集中删除该聚类中心以及属于该中心的其余三角面片，重复上述步骤，直到所有三角面片均有所属面片集。算法的具体流程如下：

(1)计算以各三角面片为聚类中心的三角面片集的测点密度均值

设定测点密度阈值α=0.001 个/mm2，则以各三角面片为中心，三角面片集的测点密度均值为

(3)

式中：δi为以第i个三角面片为中心的三角面片集的测点密度均值；ρj为第j个三角面片对应的测点密度值；函数

(4)

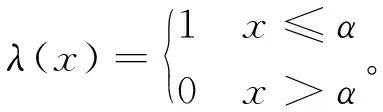
(5)

(2)求取聚类中心

计算以三角面片i为中心的三角面片集的测点密度均值与三角面片i的测点密度的残差的绝对值，以最小残差绝对值对应的三角面片为聚类中心对各三角面片进行聚类。

(3)获取测点密度大致相同的三角面片集

反复执行(1)和(2)，直到所有三角面片均有归属的三角面片集为止，用各三角面片集的测点密度均值表征该三角面片集的测点密度。基于聚类算法的一次划分获取的三角面片集如图8所示。

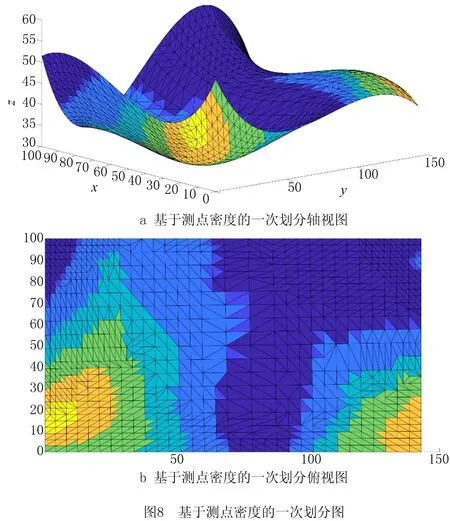
3.3 基于区域生长算法的二次划分

在对自由曲面进行一次划分并获得测点密度大致相同的三角面片集后，采用区域生长算法将其划分为相连通的子曲面，具体流程如下：

(1)建立三角面片的拓扑关系

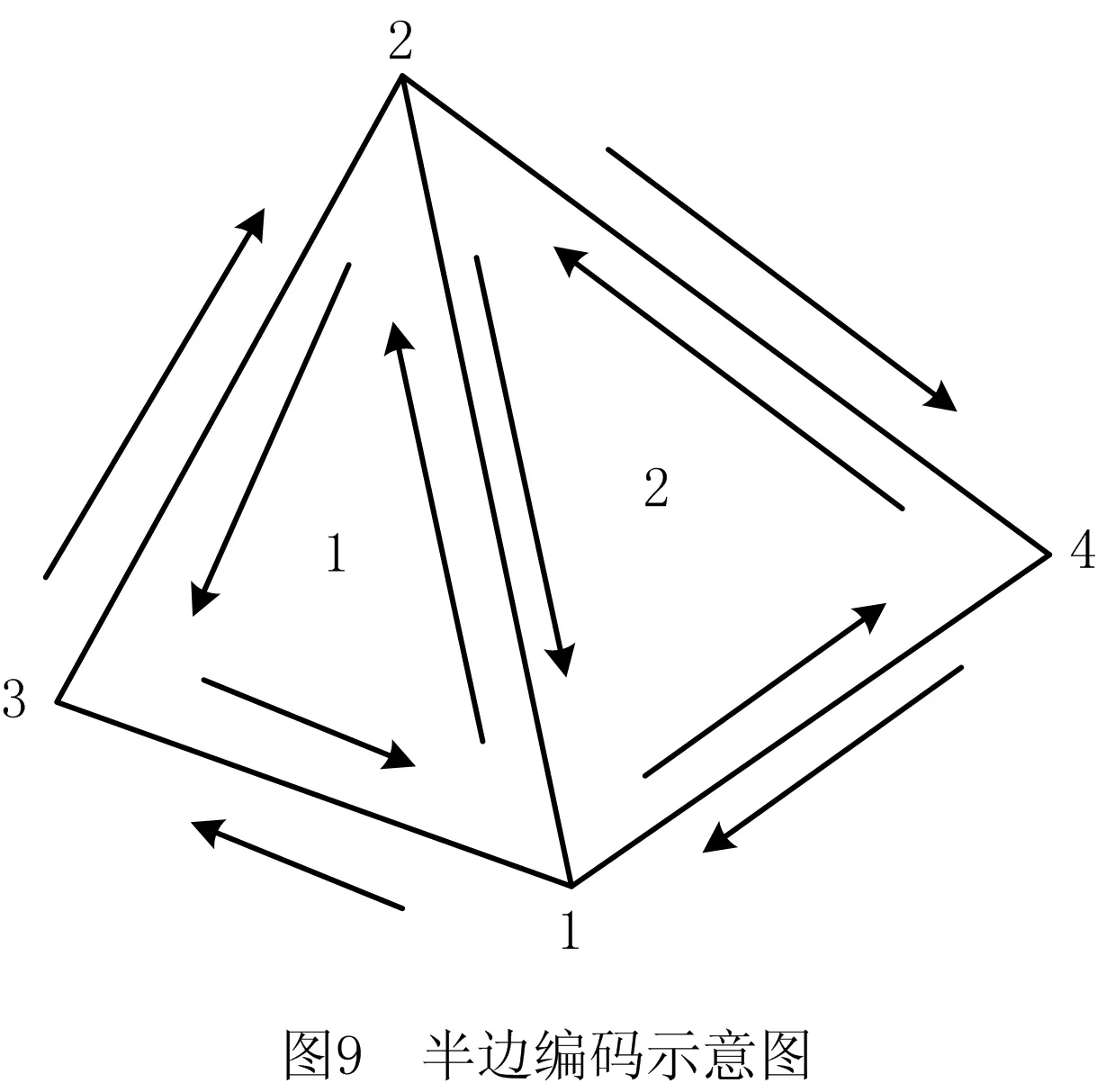
为提高区域生长算法效率，用半边编码思想对输入模型的三角面片建立拓扑关系[21]，以便查询面片的一环邻域。本文根据STL文件的特点获取各三角面片信息，生成一维数组F[i]=[P1,P2,P3]，其中：F为存储三角面片信息的数组；i表示第i个三角面片；P1，P2，P3为第i个三角面片各顶点的编号，且P1，P2，P3对应的点逆时针环绕构成第i个三角形。用半边编码思想建立二维数组B[P1][P2]=i，其中：B为存储半边所属三角面片信息的数组；P1，P2为构成半边的端点的编号；i为半边所属三角面片的编号(当半边不属于任何三角面片时i=0)。如图9所示，针对第1个三角面片，三角面片信息为F[1]=[1,2,3]，半边所属三角面片信息为B[1][2]=1，B[2][3]=1，B[3][1]=1；针对第2个三角面片，三面片信息为F[2]=[1,4,2]，半边所属三角面片信息为B[1][4]=2，B[4][2]=2，B[2][1]=2，同时B[1][3]=0，B[3][2]=0，B[2][4]=0，B[4][1]=0。若需查找第1个三角面片的一环邻域，则根据F[1]的值，按照1→3，3→2，2→1的顺序(该三角形顶点的顺时针环绕顺序)查找B数组中相应的信息，可得B[1][3]=0，B[3][2]=0，B[2][1]=2，此时第1个三角面片的一环邻域中只有第2个三角面片。

(2)根节点选取和生长准则设定

基于区域生长的二次划分主要为保证子曲面的连贯性，因此在测点数量密度大致相同的三角面片集中任意选取一个未进行二次划分的三角面片作为根节点，生长准则设定为在面片的一环邻域中、没有归属于子曲面的面片。

(3)获取相连通的子曲面

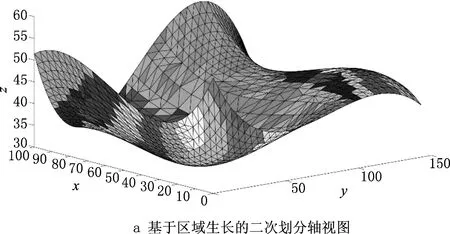
借助树状结构，首先在测点数量密度大致相同的三角面片集中选取根节点；然后从根节点开始，根据生长准则向外延展，当无法再向外延展时重新选择根节点，如此循环，直到所有三角面片均有归属的子曲面为止。基于区域生长算法的二次划分获取的子曲面如图10所示。

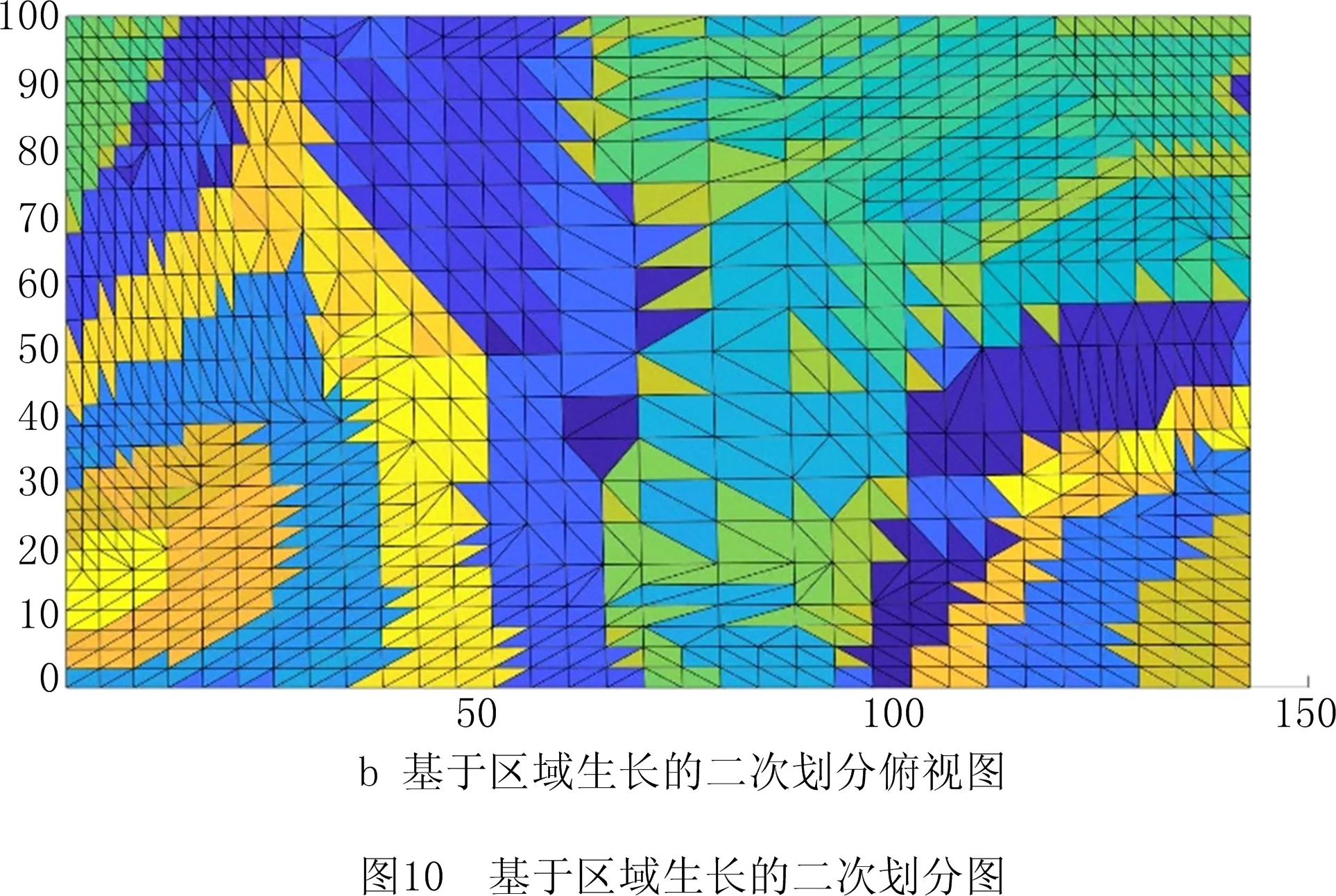
4 实验验证

4.1 自由曲面自适应测点规划实例

针对机床加工精度为0.04 mm、测量精度为

0.03 mm、公差要求为0.08 mm的自由曲面(曲面模型如图11a)，根据本文设计的自适应测点分布算法进行布点。首先，在内存中建立存储测点坐标的数据集(称为数据集A)；其次，按照本文设计的基于测点密度的自由曲面划分方法将待测曲面分割为测点密度大致相同的子曲面，并记录其对应的测点密度，如图11b所示；然后，针对每个子曲面，根据其面积和对应的测点密度计算所需分布的测点数量，再求取能够包围子曲面在xoy平面投影的最小矩形，根据矩形的长宽和所需分布的测点数量计算均匀布点所需截面的间距和测点间的步长，在截面与子曲面的截交线上根据所求步长求取各测点坐标存入数据集A，生成初始测点集，如图11c所示；最后，根据初始测点集拟合曲面，在法向偏差大于公差要求处增加测点并存入数据集A，生成输出测点集，如图11d所示。

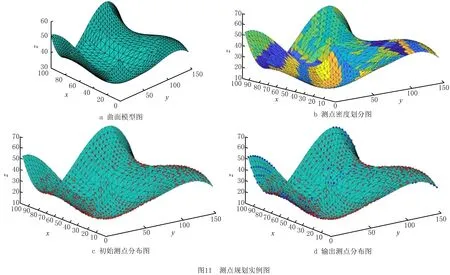
4.2 算法精度和效率对比实验

分别利用本文算法、迭代重构算法、均匀布点算法对如图12所示的曲面进行测点规划，并在牧野机床V56i上进行在线测量，以验证本文算法的精度。

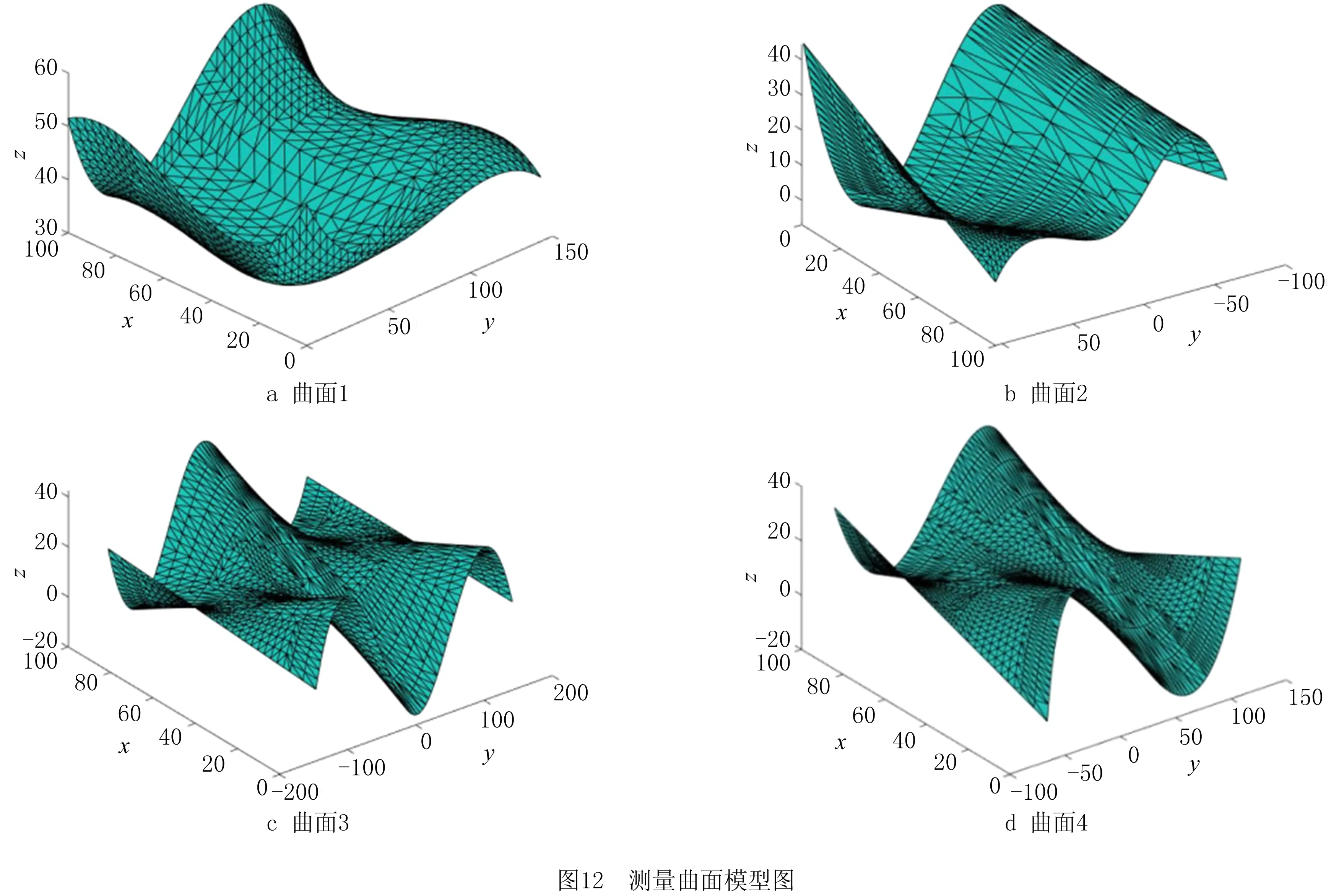
在曲面上随机分布1 200个测点并进行在线测量，获取相应测点坐标来拟合待测面的实际状态并求取相应偏差，将这些偏差值作为参照组。根据不同算法规划的测点求得的偏差值如表3所示。本文算法和迭代重构算法的误差结果均与参照组接近，但本文所需的测点数小于迭代重构算法，即采用本文算法规划测点，测量时探头所需遍历的测点数较少，测量效率较高；在相同测点数下，与均匀布点算法相比，本文算法的误差更接近参照组，即本文算法规划的测点能更详细地描述曲面。

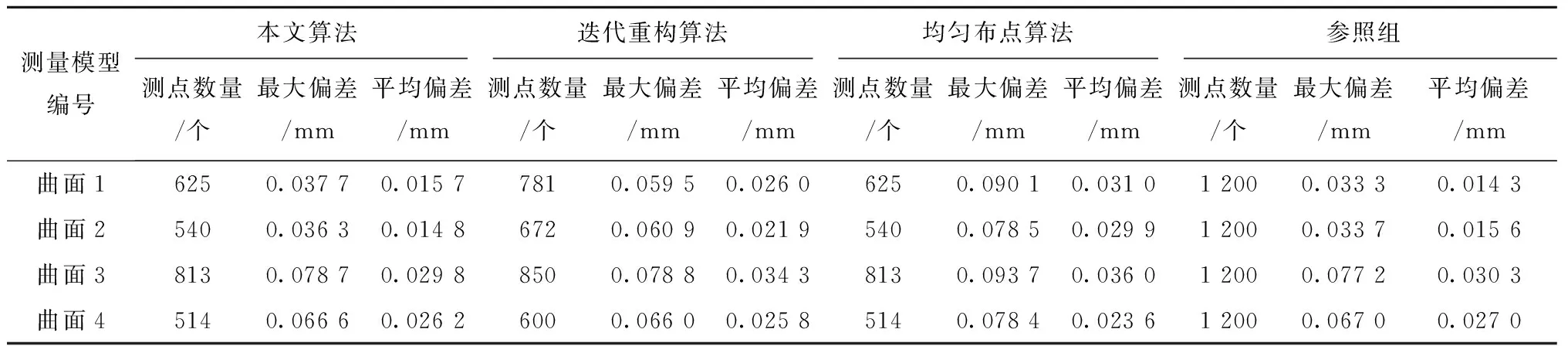
表3 不同测点规划算法误差对比表

5 结束语

本文重点研究自由曲面的三角网格模型自适应测点规划问题。首先基于机床加工精度、公差要求、测量精度、平均曲率构建测点密度预测模型；然后设定测点密度阈值，自适应获取聚类中心，将自由曲面划分为测点密度大致相同的子曲面；最后针对测点密度大致相同的子曲面均匀布点，并对测点集进行优化，从而实现三角网格模型自由曲面测点的自适应分布。本文方法的优点如下：

(1)通过曲面划分的思想，采用本文设计的测点密度预测模型精简了测点数量，并能在提高测量效率的同时保证较高的测量精度。

(2)测点密度由曲率控制，针对同一加工曲面，其机床加工精度、公差要求、测量精度近似，测点密度主要受平均曲率影响，因此本文分布的测点可反映曲面的形状信息。

(3)局部测点分布较规则，有利于测量路径规划。