基于UWB的井下人员定位算法研究

贺磊， 魏明生， 仇欣宇， 唐守锋， 李文帅， 张旭

（1. 江苏师范大学 物理与电子工程学院，江苏 徐州 221116；2. 中国矿业大学 信息与控制工程学院，江苏 徐州 221008）

0 引言

瓦斯爆炸、塌方等灾难严重威胁井下人员的生命安全，因此有必要建立有效的井下人员精确定位方案，当发生矿难时，施救人员可对矿工进行精准定位并展开营救[1]。当前井下定位技术种类较多，如RFID、ZigBee、WiFi、蓝牙等[2]。这几种定位技术基本可满足井下定位要求，但仍存在信号传输距离短、定位精度较低、功耗较高、易受外界干扰等缺陷[3-5]。超宽带（Ultra Wide Band，UWB）定位技术采用纳秒级别的脉冲信号进行通信，具有较高的时间分辨率，适用于非视距环境下的定位，且定位精度较高，与其他几种定位技术相比具有明显优势。

UWB定位基于测距原理，常用的测距算法包括单边双向测距（Single-Sided Two-Way Ranging，SS-TWR）和双边双向测距（Double-Sided Two-Way Ranging，DS-TWR）。其中SS-TWR因受时钟偏移的影响，误差较大[6-7]。DS-TWR在测距双方之间发送多条信息，获得多个时间戳，通过加长测量周期来提高测量精度[8]。井下人员定位对精度要求较高，因此适宜采用DS-TWR测距算法[9]。根据测距信息，通过位置解算算法可得到定位标签的坐标。本文通过静态实验和动态实验对加权最小二乘（Weighted Least Squares，WLS）算法[10]和CHAN[11]两种位置解算算法进行对比分析，并通过均方根误差和误差累计分布函数（Cumulative Distribution Function，CDF）综合评估定位精度。

1 DS-TWR测距模型

DS-TWR测距模型如图1所示，其中Tprop为UWB信号在定位基站与定位标签之间的传播时间，可利用定位基站和标签的时钟系统记录的时间戳T1-T3，-来计算；Tround1为基站开始发送信号到基站接收到标签信号的时间；Treply1为标签接收到基站信号到标签开始回复基站的时间；Tround2为标签开始回复基站到标签再次接收到基站信号的时间；Treply2为基站接收到标签的回复信号到基站再次发送信号的时间；Tm1，Tm2分别为定位基站和标签的系统时钟。

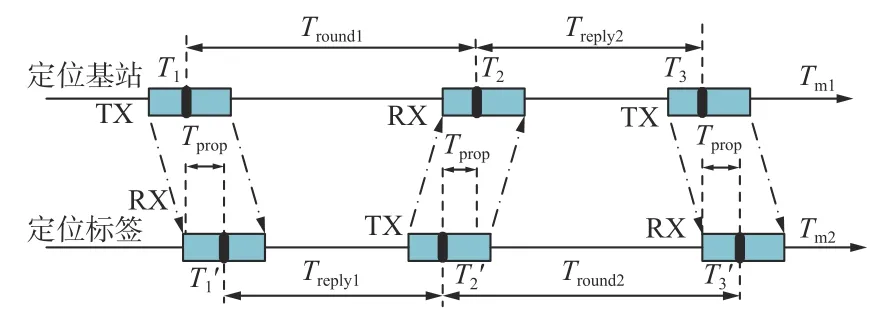
图1 矿井DS-TWR测距模型Fig. 1 Mine DS-TWR ranging model

由图1可得

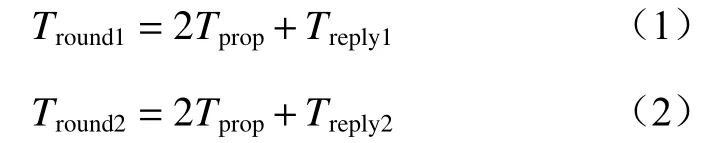
将式（1）和式（2）相乘后移项可得

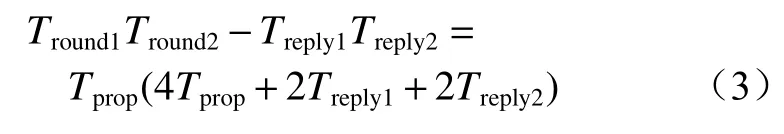
将式（1）和式（2）代入式（3）可得

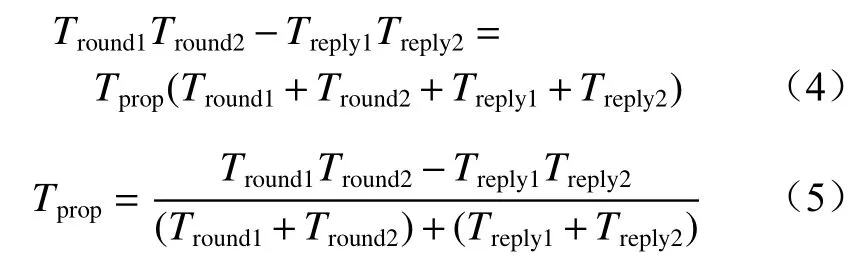
由式（5）可计算出电磁波在定位标签与定位基站之间的传播时间，结合信号传播速度可计算出传播距离。获得定位基站与定位标签之间的距离后，再通过位置解算算法计算定位标签的坐标[12]。

2 位置解算算法

2.1 WLS算法

设4个基站的坐标为（xi，yi），i=1，2，3，4，待测定位标签的坐标为（x，y），定位标签到基站的真实距离为ri，测量距离为，根据最小二乘算法可得

求解式（6）即可得到定位标签坐标的最优估计值（x,y）。

普通最小二乘算法适用于各个误差项相等的情况，由于井下UWB定位环境复杂，为了提高定位标签位置解算精度，在普通最小二乘算法中引入加权矩阵W。设定位标签到第i个 基站的测距误差为βi，则有

用测量距离与真实距离的平方差表示误差矢量：

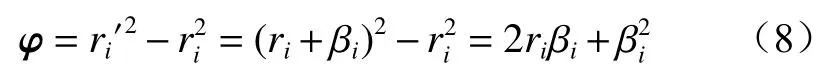
在实际应用中，测量误差远小于测量的距离，因此式（8）中的项可以忽略不计；由于不方便测量定位标签到基站的真实距离，通常利用代替真实距离ri进行近似计算。误差矢量可以进一步表示为

误差矢量φ的协方差矩阵为

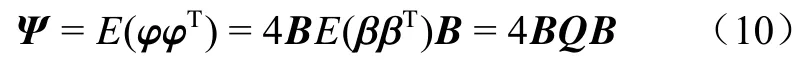
式中E为期望函数。

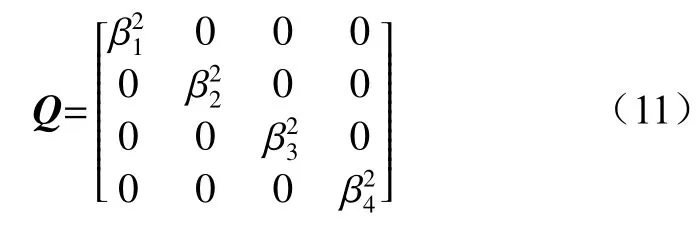
最后对Ψ求逆矩阵，得到加权矩阵W：

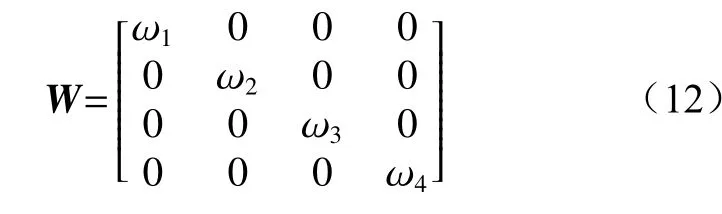
结合式（6）得到WLS算法计算公式：

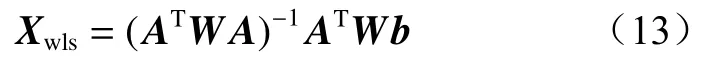
上述推导是针对4个定位基站的情况，当基站数量为4个以上时可在此基础上类推。

2.2 CHAN算法

在求解二维平面中的位置坐标时，若定位基站的数量大于3，则会有冗余测距信息，可得到2个以上非线性方程。在CHAN算法求解过程中，首先使用WLS算法估计定位标签的初始位置坐标，然后结合已知约束条件再次应用WLS算法，得到最终位置坐标估计值。

仍以4个基站为例对CHAN算法进行推导，设z=[x,y,r1]T，根据文献[13]可得

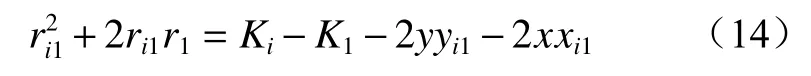
式中：ri1为定位标签到第i个基站与到第1个基站之间的距离差；；xi1，yi1分别为第i个基站与第1个基站的横坐标之差和纵坐标之差。

将式（14）改写为

当矩阵Ga可逆时z的最大似然估计值za为

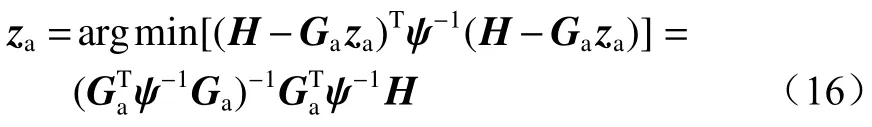
式中ψ=c2BQB，c为信号传播速度。

在实际应用中通常用Q代替ψ，则式（16）可改写为

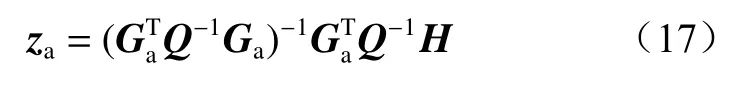
根据定位基站与定位标签之间的距离约束关系得到误差矢量：

φ1的协方差矩阵为

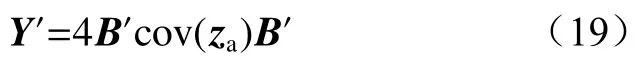
采用WLS算法对式（18）进行求解，得

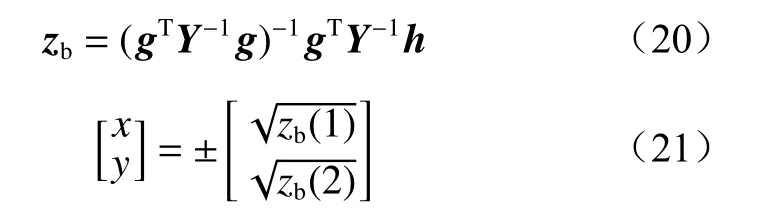
最后根据先验条件可以求得定位标签坐标估计值。

3 实验分析

为了对比分析WLS算法和CHAN算法的效果，在实验室模拟井下环境，采用4个定位基站进行实验，如图2所示。设4个定位基站BS1-BS4的坐标分别为（0，0），（560 cm，0），（560 cm，800 cm），（0，720 cm），实验设备数据更新频率为1 Hz。

图2 实验环境与自制定位设备Fig. 2 Experimental environment and self-made positioning equipment

3.1 静态实验分析

实验开始时，将定位标签放置在坐标（320 cm，400 cm）处，采集测距信息，并利用2种算法进行定位，结果如图3所示。

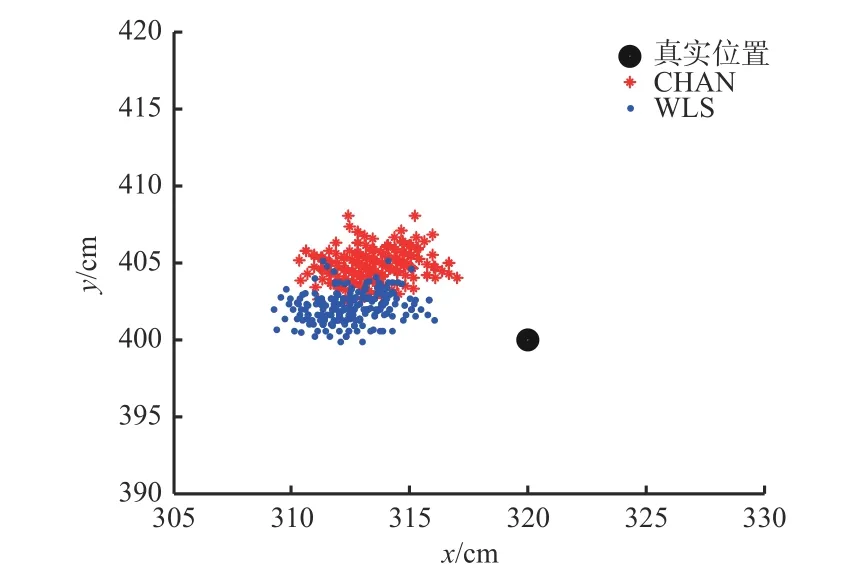
图3 CHAN与WLS算法定位结果（静态实验）Fig. 3 Positioning results of CHAN and WLS algorithms （static experiment）

计算定位标签估算位置与真实位置的欧氏距离，并绘制误差曲线，如图4所示。可看出，定位标签为静态时，CHAN算法的定位误差小于WLS算法。经计算，CHAN算法和WLS算法的均方根误差分别为5.878 6，8.007 4 cm，CHAN算法的均方根误差比WLS算法低26.59%。

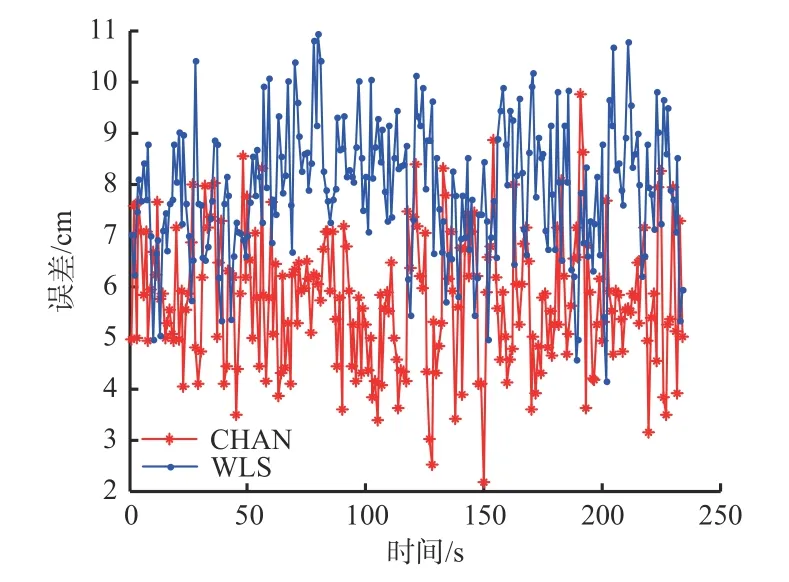
图4 CHAN与WLS算法误差对比（静态实验）Fig. 4 Comparison of errors between CHAN and WLS algorithms（static experiment）

CHAN算法和WLS算法的误差CDF曲线如图5所示。可看出，CHAN算法的误差CDF曲线在WLS算法的左上方，在设置同一误差门限值的条件下，CHAN算法的误差在门限值以内的概率较高。例如，当误差门限值取7 cm时，CHAN算法的误差在7 cm以内的概率约为80%，WLS算法的误差在7 cm以内的概率约为25%。

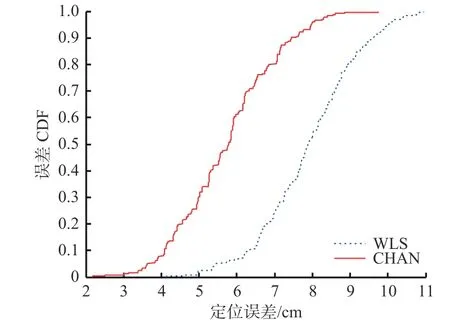
图5 CHAN与WLS算法的误差CDF曲线（静态实验）Fig. 5 Error CDF curves of CHAN and WLS algorithms（static experiment）

3.2 动态实验分析

利用移动小车搭载定位标签，模拟井下携带定位标签的作业人员。定位标签起始点坐标为（160 cm，400 cm），结束点坐标为（480 cm，400 cm），小车匀速行驶。利用CHAN和WLS算法得到的定位结果如图6所示。可看出，用CHAN算法得到的轨迹更加接近真实轨迹。

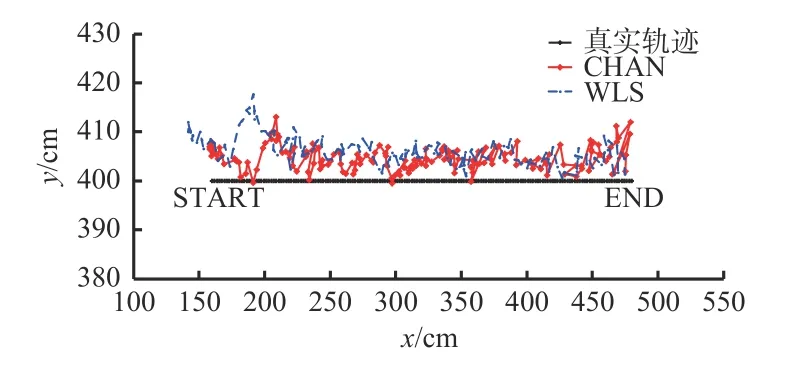
图6 CHAN与WLS算法定位结果（动态实验）Fig. 6 Positioning results of CHAN and WLS algorithms （dynamic experiment）

计算不同时刻定位标签估算位置与真实位置的欧氏距离，并绘制误差曲线，如图7所示。可看出，定位标签为动态时，CHAN算法的定位误差小于WLS算法。经计算，CHAN算法和WLS算法的均方根误差分别为12.292 3，21.180 9 cm，CHAN算法的均方根误差比WLS算法低41.97%。

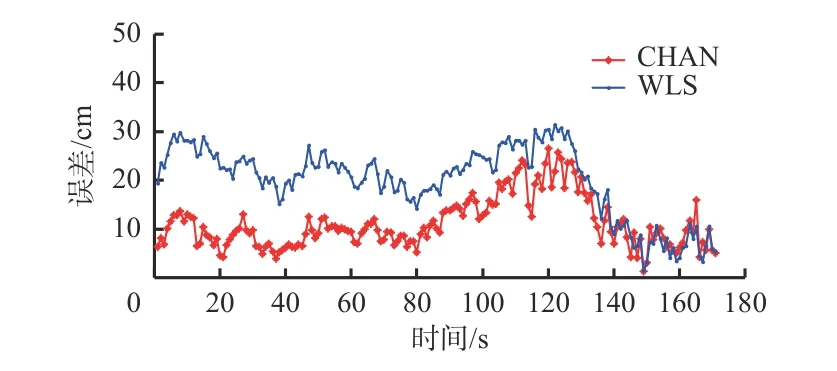
图7 CHAN与WLS算法误差对比（动态实验）Fig. 7 Comparison of errors between CHAN and WLS algorithms（dynamic experiment）

CHAN算法和WLS算法的误差CDF曲线如图8所示。

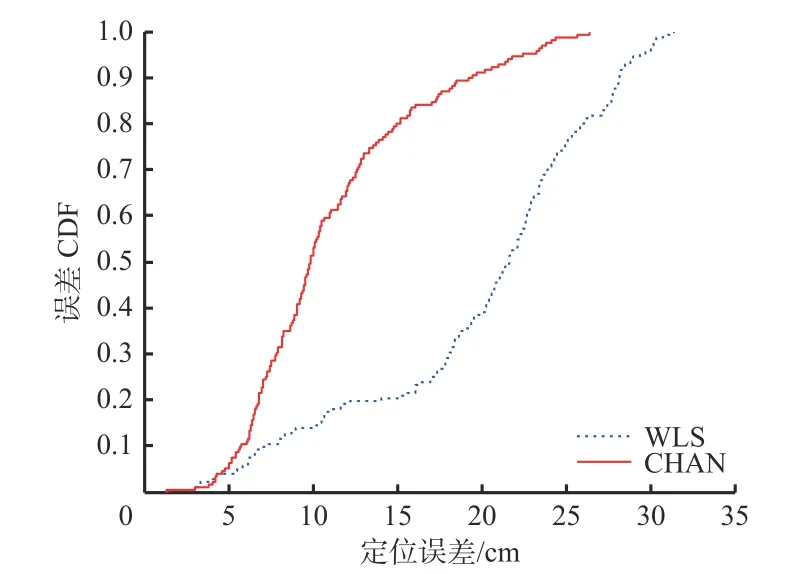
图8 CHAN与WLS算法的误差CDF曲线（动态实验）Fig. 8 Error CDF curves of CHAN and WLS algorithms（dynamic experiment）

从图8可看出，CHAN算法的误差CDF曲线基本在WLS算法的上方，说明在动态实验中CHAN算法的定位精度高于WLS算法。

4 结语

研究了基于UWB的井下人员定位算法。采用DS-TWR方式测量定位基站与定位标签的距离，利用WLS算法和CHAN算法对静态测距信息和动态测距信息进行解算，最后通过均方根误差和误差CDF综合评估2种算法的定位性能。实验结果表明：静态实验时，CHAN算法和WLS算法的均方根误差分别为5.878 6，8.007 4 cm，CHAN算法的均方根误差比WLS算法低26.59%；动态实验时，CHAN算法和WLS算法的均方根误差分别为12.292 3，21.180 9 cm，CHAN算法的均方根误差比WLS算法低41.97%；CHAN算法的定位精度高于WLS算法，更加适用于煤矿井下人员定位。