孔压静力触探在砂土液化评价中的应用研究
2022-07-07邓义龙
邓义龙
(武汉市勘察设计有限公司,湖北 武汉 430022)
0 引 言
地震液化是由于地震震动或其他动荷载导致土层强度和刚度降低甚至丧失的现象,在饱和粉细砂和粉土中尤为明显[1,2]。土层的地震液化在世界范围内都是一个严重的地质灾害问题,引起巨大破坏,常见液化表现包括“砂沸”、地表沉降、建筑物倾斜或倾覆、陡坡溜滑、土层侧向挤出等。目前学界对于地震液化的研究还处于初步阶段,这与天然地质体的复杂程度有关,也与计算方法及实际地震的重复验证性差有关[3]。
尽管如此,对砂土的液化势评价方法可以归结为两大类。其一为确定性计算方法,Seed等[4]利用定量方法推导出目前最为公认的液化评价公式,另一种方法是概率计算方法,Juang[5]和Moss[2]等利用统计学理论建立了大量的估算液化的概率模型。
本文基于上述两种计算方法,依托于某跨长江公路连接工程的静力触探数据进行砂土液化判别,分析两种方法的计算适用性和精确度。
1 基于孔压静力触探的砂土液化基本原理
1.1 确定性计算方法
确定性方法评价砂土液化的主要思想是比较给定深度处的土体的循环抗力比(CRR)与地震诱发的循环应力比(CSR)。在地震震级为7.5时,如公式(1)所示:
(1)
式中:amax为地震峰值水平加速度;g为重力加速度;σv0为初始垂直总应力;σ′v0为初始垂直有效应力;rd为应力折减系数;MFS为震级比例因子。
循环抗力比CRR采用孔压静力触探数据进行计算,如公式(2)、公式(3)所示。
CRRc=0.833[(qc1,N)cs/1000]+0.05 (qc1,N)cs<50
(2)
CRRc=93[(qc1,N)cs/1000]3+0.08 50≤(qc1,N)cs<160
(3)
式中:(qc1,N)cs为针对细粒含量的标准锥尖阻力修正。
因此,联合公式(1)~公式(3),按公式(4)计算安全系数Fs进行液化势判别:
Fs=CRR/CSR
(4)
1.2 概率计算方法
循环应力比CSR的计算仍采用公式(1),循环抗力比CRR和液化概率分别按公式(5)和公式(6)计算:

(5)
(6)
式中:Φ(PL)为累积正态分布;Φ-1(PL)为逆累积正态分布。
qc1=Cqqc
(7)
(8)
式中:Cq为锥尖归一化系数;c为归一化指数,如公式(9)所示。
(9)
其中:
(10)
2 工程概况
某跨长江公路连接工程起于洪湖市乌林镇,起点桩号为K20+700,止于赤壁市沧湖开发区,终点里程为K31+900,拟订方案线路全长13.263 km,其中长江大桥总长5.572 km(主桥长1 380 m)。
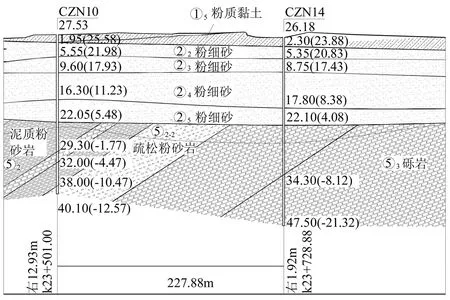
图1 场区地质纵断面
研究区段的上覆土层主要为①5粉质黏土、②2粉细砂、②3粉细砂、②4粉细砂、②5粉细砂。各砂土层分布稳定,厚度均匀。在颗粒组成上,各粉细砂层的颗粒大小含量差异较大,对于大于0.075 mm且小于0.25 mm的颗粒含量平均值,②2层粉细砂的最小,为60%,②5层粉细砂的最大,为80.8%,②3层粉细砂与②4层粉细砂的相近,分别为72.6%、77.1%。②2层粉细砂与②3层粉细砂的黏粒含量平均值相近,分别为3.8%、4.6%,②4层的黏粒含量平均值最大,为16.3%,②5层的黏粒含量平均值最小,为1.5%。
3 测试成果分析
图2~图4分别为孔压静力触探实测锥尖阻力qc、侧摩阻力fs、孔隙水压力u2随深度变化曲线。
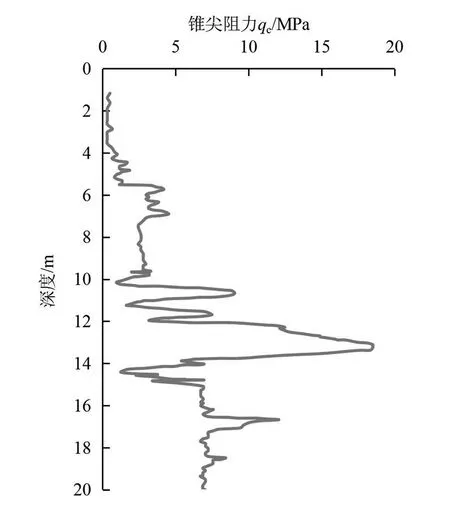
图2 锥尖阻力随深度变化曲线
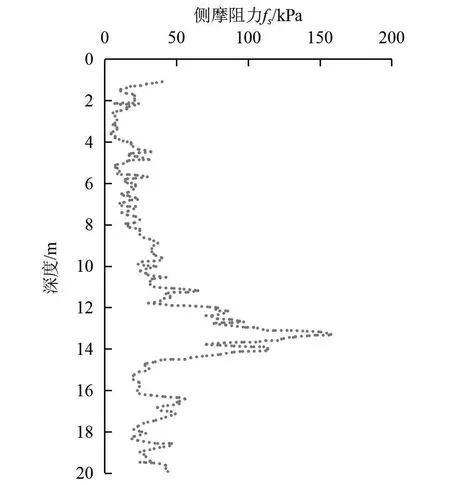
图3 侧摩阻力随深度变化曲线
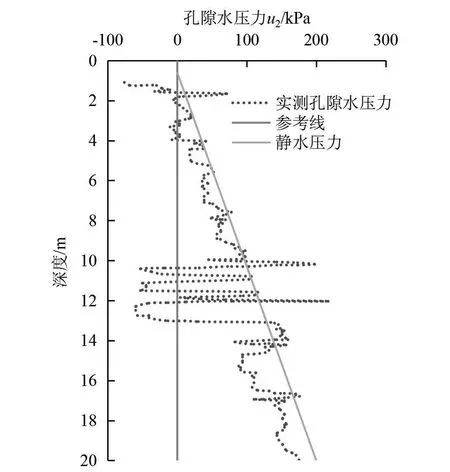
图4 孔隙水压力随深度变化曲线
在如图1所示的钻探揭示地层条件下,在孔压静力触探试验位置处地层分别为:0~2.00 m为①5层粉质黏土、2.0~5.50 m为②2层粉细砂、5.50~9.50 m为②3层粉细砂、9.50~15.00 m为②4层粉细砂、15.00~22.00 m为②5层粉细砂。从图2、图3中可以看出,锥尖阻力与侧摩阻力能够准确地反映各地层的力学特性,不同土层的锥尖阻力曲线呈现不同的斜率和数值大小变化,连续测试的数据能够对地层起到精确的划分,各土层的平均锥尖阻力和平均侧摩阻力见表1。从图4中可以看出,各砂层的孔隙水压力与静水压力相近,在10.0~13.00 m范围内波动较大,这与该段的黏粒含量较大有关,总体上表明各砂层的含黏粒较少,透水性好。

表1 各层锥尖阻力与侧摩阻力平均值
图5、图6分别为安全系数Fs与液化概率PL随深度的变化。
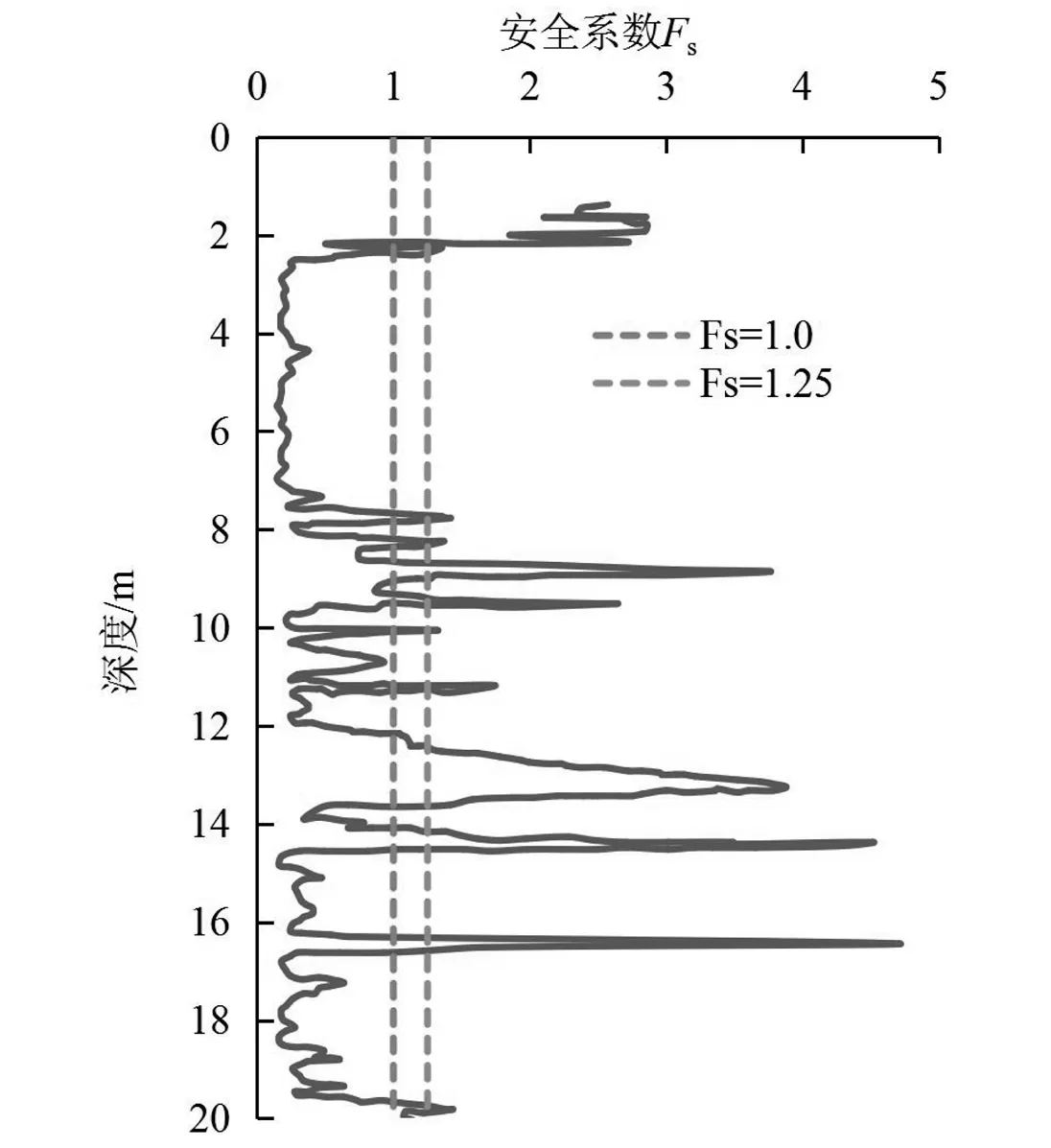
图5 安全系数随深度变化曲线

图6 液化概率随深度变化曲线
从图中可以看出,无论是利用何种判别方式,把①5层粉质黏土判定为不液化土层,都与事实是相符合的,同时也表明,两种判别方式不仅适用于砂土也适用于一般的土层判别。从图5中可以看出,②2层粉细砂其安全系数皆小于1.0,且数值起伏波动较小,而②3层粉细砂、②5层粉细砂的黏粒含量与②2层粉细砂相近,但颗粒大小组成不同,②3层粉细砂、②5层粉细砂的安全系数都呈现不同程度的起伏波动,安全系数基本小于1.00,少部分介于1.00和1.25之间,而②3层粉细砂与②5层粉细砂的黏粒含量相近,但各砂层颗粒组成相差较大,小于0.075 mm的颗粒含量平均值按②2层粉细砂、②3层粉细砂、②5层粉细砂依次减小,②3层粉细砂比②5层粉细砂的安全系数离散性更大。由此表明,砂土的颗粒成分组成对砂土的液化势影响显著,小于0.075 mm的颗粒含量越大,其具有液化的可能性也越大。另一方面,对比②3层粉细砂、②4层粉细砂可知,两者的颗粒成分组成相近,而黏粒含量前者明显小于后者,导致后者的安全系数曲线波动更大,Fs最大值为3.51,最小值为0.28,因此黏粒含量也是影响砂土液化势的重要因素,黏粒含量越低,液化可能性越大。类似地,从图6中也可以得到相似结果。
对比图5和图6可知,两种方法对②2层粉细砂的判别基本一致,而对于②5层粉细砂,采用确定性计算法,安全系数Fs基本小于1.0,判别结果为敏感度高,而采用概率计算方法,则在(0.65,0.85),(0.65,0.85)区间都有,判别结果分别为可能液化和液化,因此,采用概率计算方法的计算结果更为精细。对比②4层粉细砂、②5层粉细砂,两者的颗粒成分组成相近,而黏粒含量前者明显大于后者,概率计算方法对黏粒含量更为敏感。
进一步地对比两种计算方法的精确度,将概率计算方法构建为传统的概率曲线等高线,并将确定性计算的安全系数Fs=1.0等高线也显示在图中,如图7所示。
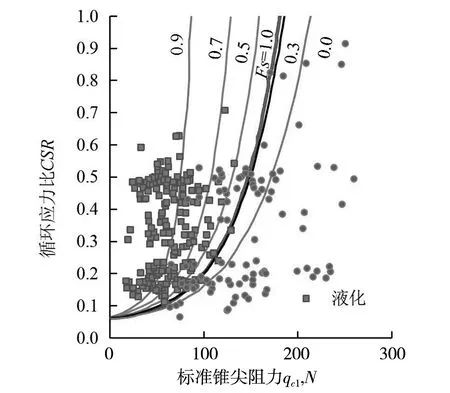
图7 不同方法计算结果对比
从图7中可以看出,安全系数Fs=1.0等高线与液化概率PL=0.3相近,安全系数对于Fs的判定结果更为保守。
4 结 论
本文依托某跨长江公路连接工程的静力触探数据进行砂土液化判别,分析两种方法的计算适用性和精确度,得出以下结论:
(1)采用孔压静力触探测试获得的锥尖阻力与侧摩阻力能够准确地反映各地层的力学特性,连续测试的数据为两种液化势判别方法提供了良好的计算基础。
(2)两种计算方法皆表明,砂土的颗粒成分组成和黏粒含量对砂土的液化势影响显著,细颗粒含量越大,黏粒含量越少,其具有液化的可能性也越大。
(3)两种判别方式不仅适用于砂土,也适用于一般的土层判别,相比于确定性计算方法,概率计算方法对黏粒含量更为敏感,且计算结果更为精细,前者计算结果更为保守。
