一种基于稳定平台的复合控制模型研究
2022-07-07沈佳琪
沈佳琪,姚 力
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225001)
1 工作原理
控制系统的本质是由各功能模块进行相互数据链接并形成反馈系统[1],核心是数据处理和反馈校正流程,按照功能特性可分为五个部分:数据采集、信号处理、反馈控制、部件响应和通信模块。数据采集指控制系统中的传感器通过各自不同的特性进行数据感知、解析和汇总,将采集的数据经通信总线进行传递;信号处理指控制系统核心处理单元对数据进行判定和适用的过程,输出端为反馈控制模块;反馈控制指通过控制算法的应用对系统组件进行控制操作,将输出信号PWM传送给驱动器,控制稳定平台电机响应;部件响应为电机控制运作;而通信模块为各组件之间数据传输的桥梁。本文将重点对反馈控制模块进行研究,对控制方式和控制算法进行推导,建立完整的复合控制模型,达到稳定平台精准控制的工程实用价值的目的。
2 控制方式
反馈控制模块通过控制流程和控制算法完成正反馈和负反馈,其中控制流程中完善的控制方式和合理的组件搭配是提高控制精确性的主要途经,本节将对控制方式中的稳定回路、跟随回路和校正回路原理进行分析。
(1)稳定回路。稳定回路是最快速的反应回路,也是稳定平台控制的中枢回路[2],可在最短的时间内保持平台的稳定状态,由电流环和速率环为核心组成部件,采用感应电阻和陀螺对控制环进行数据采集和信息反馈,对其数据采集信息进行实时校正。电流环属于快速微调稳定环,而速率环则是稳定控制的基准调节环,通常处于基准平衡调节状态,二者配合可快速对控制系统进行精准的稳定控制。
(2)跟随回路。跟随回路是控制系统的主动任务执行机构,编码器位移环为核心组成部件,是稳定平台性能状态的主要体现,通常采用较为精准的编码器作为数据采集部件,执行步骤分为数据采集、位移扫描和反馈修正,通过编码器的位移锁定可确定当前位移状态,通过编码器位移转换可进行目标位移跟随和正向反馈数据响应。
(3)校正回路。校正回路的本质是通过图像比对器或图像跟踪器对目标进行定位、跟踪、校正的控制回路,以图像位移环为核心组成部件,主要依据图像脱靶量和像素匹配点进行控制,采用图像比对器对控制环进行数据采集和信息反馈,是控制系统的被动任务执行机构。
3 控制算法
提高控制系统的精度除了采取优化控制系统的控制方式,还有一种方法则是选择控制精度更高的算法加强系统控制黏性。本节通过研究各控制算法的原理特性和优缺特点,设计了一种复合控制算法,提高控制系统的控制精度和稳定性。
(1)传统PID控制算法。此算法是经典控制算法,其核心是直接对控制采用PID等效措施,通过比例、积分、微分的方式调整模型的控制阈值和当前状态值,进行范围、正负反馈数值变换,快速适应后续任务的控制要求。优点是逻辑简单、方式直接,可快速完成控制措施;缺点是控制的变化幅度较大,稳定性较差,在临界值会造成控制抖动和反转的错误控制状态。
(2)自适应控制算法。自适应控制算法是一种通过冗余数据的辨识和修正,不断对预期值进行数据归拢和训练,以决策方式进行数据判定和界定,通过规则的适用性不断改进状态参数,以达到满足一定要求控制变量的控制算法。其核心设计为决策机构、修正机构和辨识策略的自适应判别。
自适应控制算法优点是数据控制平滑、数据延展性和鲁棒性较好、数据控制期望值较高;缺点是数据完整性较差,数据突变性减弱,大范围变化会导致控制部分缺失,控制反应较慢。
(3)模糊控制算法。模糊控制算法又称仿生控制算法,依托先验信息进行一定范围的数据推导并形成模糊规则,将控制变量和处理数据进行隶属分类模糊化,进行最直接的控制范围确认,最终通过反变化得到解模糊后的控制数据,核心是模糊推理和模糊量类比区分,原理如图1所示。

图1 模糊控制算法流程图
设模糊量E的输入集合为,量化分类参数为,则:

知识库即为先验信息,在一定的模糊化数据解析过程中,将变量数据进行推理换算,同时加入量化分类参数对其进行模糊区分,本文选择较为常用的加权平均法和累加乘积方式进行解模糊变化,对量化分类参数进行精确量确认,设精确量U的输出集合为,则:

模糊控制算法的优点是通过先验信息快速、有效地对控制量变化进行判断和修正,在先验信息准确的情况下数据跳变状态较为平稳;缺点是在模糊化和解模糊化时不在模糊隶属参数规定范围内的数据将丢失,需要进行数据补偿和模糊量化参数的修正和扩展。
(4)复合控制算法。复合控制算法的本质是一种将各单源控制算法的优点处理方式进行综合,采取直接进行PID控制,自适应调整并修正配置参数,以模糊控制算法为流程设计的方式对各控制算法进行有机的数据融合策略的综合控制算法。在控制数据处理过程中,对量化参数、隶属数据集配比参数、模糊先验信息置信度参数等进行自适应控制和修正,以模糊推理进行模糊规则确定,采用模糊化和解模糊化的方式对PID控制数值进行精确性控制。在复合控制算法的实际操作中,主要分为四部分流程:第一,对实际受控输入数据按照模糊控制机理进行模糊化,并在先验信息中进行模糊推理,确定模糊规则;第二,对控制变量和控制参数按照自适应辨识策略要求进行数值匹配,调整PID控制参数,对补偿数据和过调数据进行判定和修正,加载冗余信息和隶属函数范围量;第三,对自适应期望值进行更新,对置信参数进行调整,按照解模糊化流程对PID控制量值进行数据处理;第四,将调整后的PID控制量值输出,并将调整量值反馈到模糊控制规则中,进行参数校准和阈值控制。得到的PID精控制量值计算公式如下:

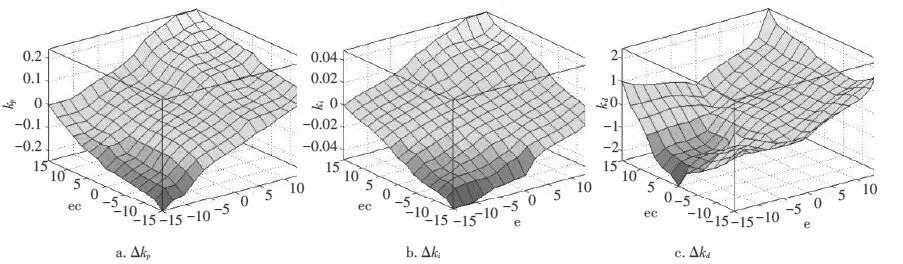
图2 变量的模糊控制隶属范围模型图
4 算法仿真
本节在同一数学模型的基础上,通过类比的方式对复合控制算法的状态和优势进行实际的算法仿真测试,采用直观性较强的阶跃信号进行控制算法效果对比试验,设置俯仰角为静止标校零位,通过突变在数据记录时间位产生偏移量为1°的阶跃响应,产生时长为3 s,依次将各控制算法和复合控制算法进行软件编程并烧录进控制器中,将数据存储单元的数据通过通信总线导出,在仿真软件中对数据进行复验和多点描绘,按10 ms的频率周期进行点位串联,可得到不同算法的仿真实验图如图3所示。

图3 阶跃响应算法类比试验图
由图3可知,从阶跃响应时间记录点开始,真实偏移是一个持续3000 ms的1°偏移曲线,传统PID控制算法响应迅速,但由于其控制精度差,所以在阶跃响应时产生了较为明显的跳变反应;模糊控制算法虽受模糊的反变化效应很好地降低了跳变冲量,但由于其控制是建立在去除范围之外数据集的基础上进行的,所以数据量不完整,随着时间的延续和先验信息的不完整,稳定度较低,控制量将会不断振荡;复合控制算法较好的规避了前两者的控制问题,反应迅速,收敛性强,且无跳变反应,由于自适应的不断修正,随着时间的延续控制量趋于期望值,控制精度高,达到了控制算法研究的预期测试目标。
5 环路测试
环路测试选取稳定平台的俯仰轴进行实际控制环路测试,保证双框架其余转向角的共振要求,平衡速率回路和位移回路的偏移量影响,将稳定回路设置为一阶惯性测量环节,无过频变量和超调变量干扰,关闭校正系统的数据截取,选取最大范围的数据集作为稳定测量数据集。本文只针对俯仰轴的稳定回路进行复合控制算法环路测试,不考虑其他模型影响,研究并分析稳定平台的稳定精度。设置稳定平台俯仰轴以正弦波的方式进行振动,振动的频率为1 Hz,持续振动5 s,偏移弧度值为8×10-4rad,将振动期间的控制输出值进行数据采集,按照数据采集原点进行数据记录,可得指向精度数据记录如图4所示。
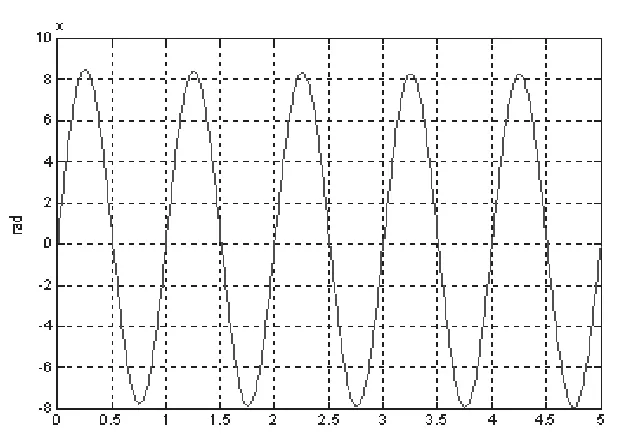
图4 控制稳定指向精度示意图
同时,在俯仰轴进行稳定控制时,确定其相频特性可知,在1 Hz的振动干扰下,控制变量较实际量值有时序差,但不影响修正变量的幅值特性,在带宽为118 Hz的稳定环控制过程中,其增益功率为-2.97 dB,指向精度的范围不超过实际测量值的85%,则稳定平台的俯仰轴稳定回路频率特性分析如图5所示。

图5 频域拐点特性示意图
由图4和图5可知,环路测试在时域和频域过程中满足复合稳定平台的稳定精度,证明了复合控制算法的精确性和复合控制模型的适用性。
6 结束语
本文从整体阐述了复合控制模型的工作原理和控制方式,采用一种新型的复合控制算法提高了控制模型的实际控制精度和稳定性,通过算法仿真和环路测试证明了算法和模型结构的正确性和适用性,具有较高的工程实用价值。■
