基于遗传算法的工业机器人定位参数误差研究

王文博，李 岸

影响工业机器人绝对定位精度的因素有很多，大致可以分为三个因素：负载、参数和环境，其中参数的影响因素占到机器人定位误差的80%以上。因此，为了提高工业机器人的定位精度，必须尽可能得出准确的运动学参数。目前广泛认可的方法有最小二乘法、Levenberg-Marquardt 算法[1]、扩展卡尔曼滤波法、最陡梯度搜索算法等经典算法，但都受限于计算量大[2]，忽略的误差因素过多等而不能有效减小机器人的定位误差。本文采用遗传算法识别机器人的参数误差，利用遗传算法的进化搜索特性，可以对机器人参数值进行较准确辨识，满足机器人的工作要求。

1 运动学建模与建立误差模型

本文研究对象为KUKA KR270R2700 型机器人（见图1）。

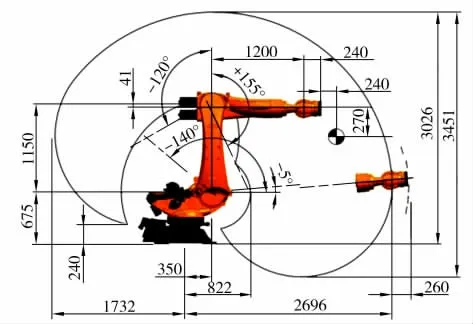
图1 机器人外形尺寸和运动范围

设定机器人两两相邻连杆坐标系的运动学变换参数，以ai-1表示连杆的长度，以αi-1表示两个相邻坐标系中两z 轴的夹角，以连杆偏置di表示两连杆间的最短距离，以关节转角θi表示连杆坐标系两个x 轴的夹角（见表1）。

表1 机器人D-H 参数

本文分析对象为六自由度机器人，则机器人末端连杆相对于固定基座的转换矩阵可以表示为：

2 基于遗传算法的误差参数辨识仿真

图2 遗传算法运算流程

交叉算子 选用算数交叉方式可以更好地适应浮点数编码。

变异算子 本文选用高斯变异方式以改善算法的局限性。

将遗传算法通过matlab 软件实现，设置种群内个体数目N=100，因为六自由度机器人所需辨识的参数有24 个，所以种群内染色体数目为24，初始交叉率为0.6，初始变异率为0.2，种群优化迭代最大次数为1 000 代。

笔者对工业机器人进行预先设定几何模型参数的误差值（见表2）。

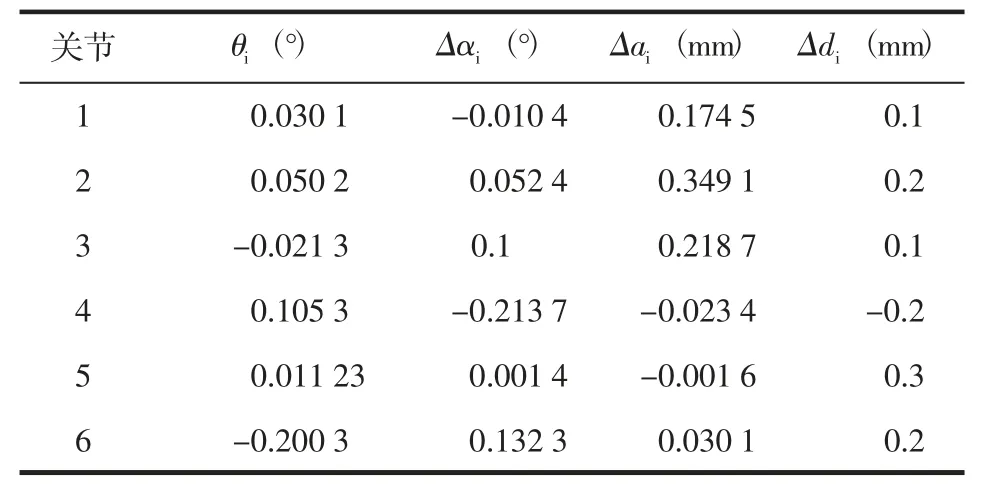
表2 预设参数误差值

笔者选择机器人运动空间中的几组关节角，将表2 中的预设误差值与表（1） 中的D-H 参数值相加作为机器人实际运动学参数代入式（1） 和式（2），求解出这几组关节角分别对应的机器人末端所到达的位置作为实际运动位置。

在运行遗传算法时，尽可能使适应度函数趋近于0，使理想位置趋近于实际位置，将识别出来的参数误差值与预设误差值相比较即可验证算法的正确性[5]。

由迭代图可知遗传算法在迭代到200 代左右时适应度函数就已经趋近于0（见图3），采用遗传算法识别得到的机器人运动学参数误差（见表3）。

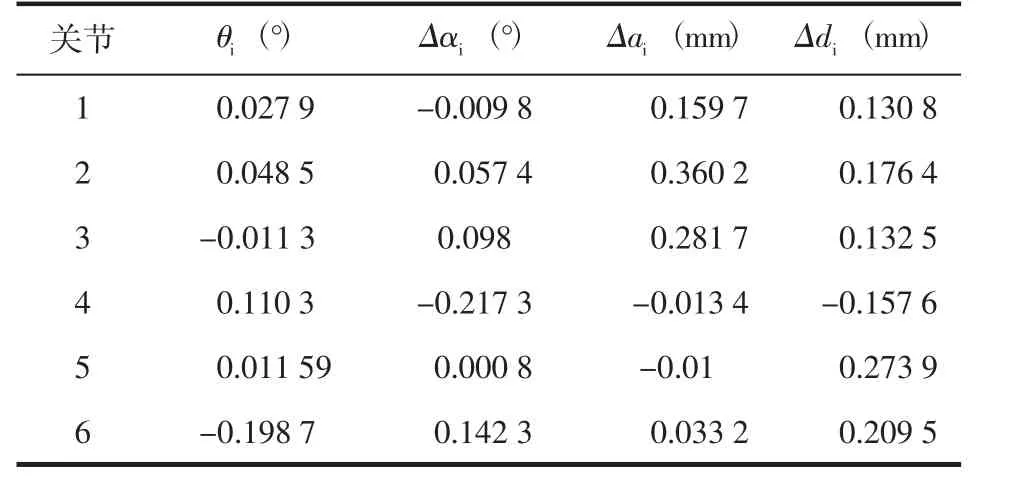
表3 遗传算法识别出的误差值

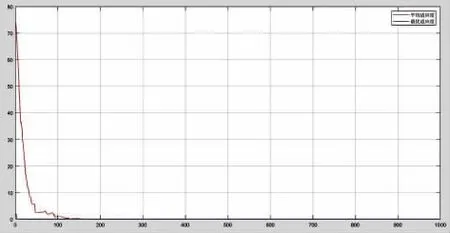
图3 迭代结果

可知，由遗传算法辨识得到的结果可以使机器人末端位姿趋近于实际位姿，而且遗传算法辨识出的参数误差值与预设参数误差值基本一致，证明使用遗传算法在本课题求解的可行性。

3 结 语

本文通过仿真验证所建立机器人运动学模型的准确性，使用遗传算法对推导得到的机器人运动学参数误差值进行计算。结果表明，采用遗传算法对机器人进行参数辨识是可行的。