经典Marr-Hildreth边缘检测的量子实现
2022-07-07鲍华良
鲍华良, 赵 娅
(东北石油大学 计算机与信息技术学院, 黑龙江 大庆 163318)
量子图像处理是融合数学、 量子计算、 量子信息、 图像处理等形成的交叉学科[1], 其包括量子图像描述模型和量子图像处理算法两方面. 量子图像描述模型主要包括量子栅格描述[2-3]、 实矢量(real ket)描述[4]、 灵活的量子图像描述(flexible representation of quantum images, FRQI)[5]、 新的增强量子图像描述(a novel enhanced quantum representation, NEQR)[6]、 对数极坐标图像的量子描述[7]等. 量子图像处理主要包括图像置乱[8-9]、 图像加密[10]、 图像隐藏[11]、 图像水印[12-13]、 量子电影[14]、 量子音频[15]、 图像匹配[16]、 图像定位[17]、 几何变换[18]、 颜色处理[19]、 特征提取[20]、 边缘提取[21]、 边缘检测[22]和图像分割[23]等. 在量子图像边缘检测方面, 目前文献报道相对较少.
在经典的边缘检测中, 一些算子(如Gauss-Laplace滤波(LoG))涉及大量的有理数乘法运算, 而如何设计这些算子的量子线路目前文献报道较少. 文献[24]提出了基于Laplace算子和零交叉法的量子图像边缘提取方法, 具有较强的指导意义. 但文献[24]在下列两点上有进一步的改进空间: 第一, 因为Laplace算子本质上是一种锐化滤波器, 而不是平滑滤波器, 所以使用Laplace算子对原始图像进行平滑处理并不理想; 第二, 文献[24]未给出零交叉提取的算子线路设计方法.
本文研究经典Marr-Hildreth边缘检测对应的量子实现方法, 该方法包括两个核心过程: Gauss-Laplace滤波和零交叉提取. 通过设计这两个核心过程及若干辅助算子的量子线路, 利用量子计算的并行性, 该方法可实现对经典方法的指数级加速. 经典计算机上的仿真实验验证了该方法的有效性.
1 预备知识
1.1 经典Marr-Hildreth边缘检测
Marr-Hildreth边缘检测是经典图像边缘检测的一种重要方法. 该方法的核心是Gauss-Laplace滤波器2G, 可表示为

(1)
经典图像处理中的Marr-Hildreth边缘检测方法, 先对一张图像f(x,y)采用LoG滤波器实施卷积, 表示为
g(x,y)=[2G(x,y)]*f(x,y),
(2)
然后寻找g(x,y)的零交叉点, 从而确定f(x,y)的边缘位置.
在任意像素p处的零交叉表示至少有两个相邻像素的符号不同, 共有4种情况需要测试: 左/右、 上/下以及两个对角线.实施时通常先设置一个阈值, 当且仅当相邻像素灰度值差的绝对值大于该阈值时, 像素p才为一个零交叉像素.
1.2 NEQR模型
对于一张2n×2n的灰度图像, NEQR模型采用(2n+q)个量子比特描述, 其中q个量子比特描述像素灰度值, 2n个量子比特描述像素位置, 表示为

(3)


图1 2×2的灰度图像及对应的NEQR表示Fig.1 Gray-scale image of 2×2 and its NEQR representation
1.3 补码定义
LoG滤波罩通过对式(1)采样生成, 所以采样数据有符号分数, 为便于运算, 本文采用补码表示. 下面给出补码定义.
设x为一个(n+1)位的二进制数, 包括1个符号位(0表示“+”, 1表示“-”),m个整数位xm-1,xm-2,…,x0以及(n-m)个小数位x-1,x-2,…,xm-n.x的补码[x]c定义为

(4)


(5)
在本文设计的各种模块中, 所有与像素灰度值有关的数据都将用二进制补码表示.
1.4 量子比较器
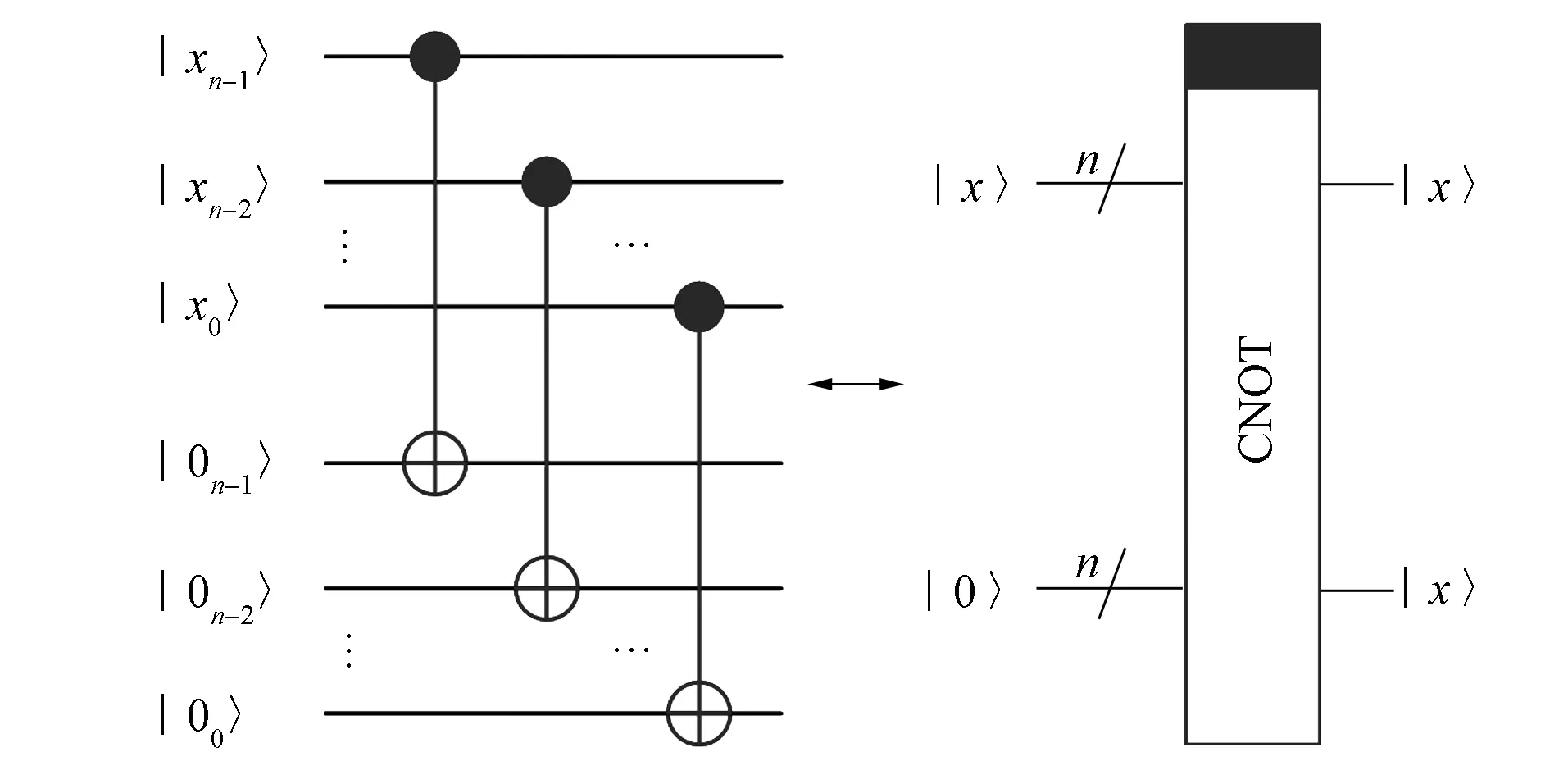
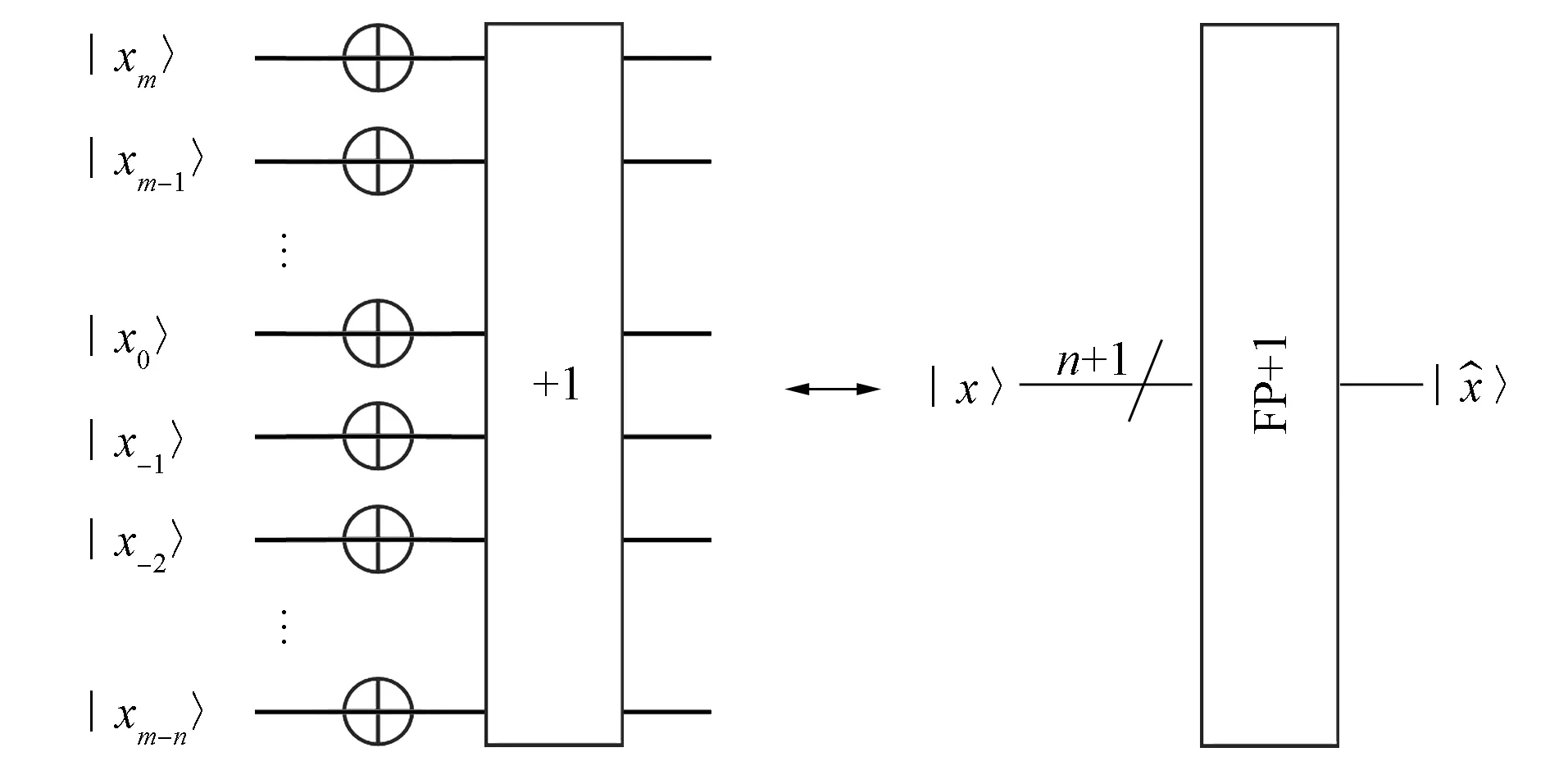
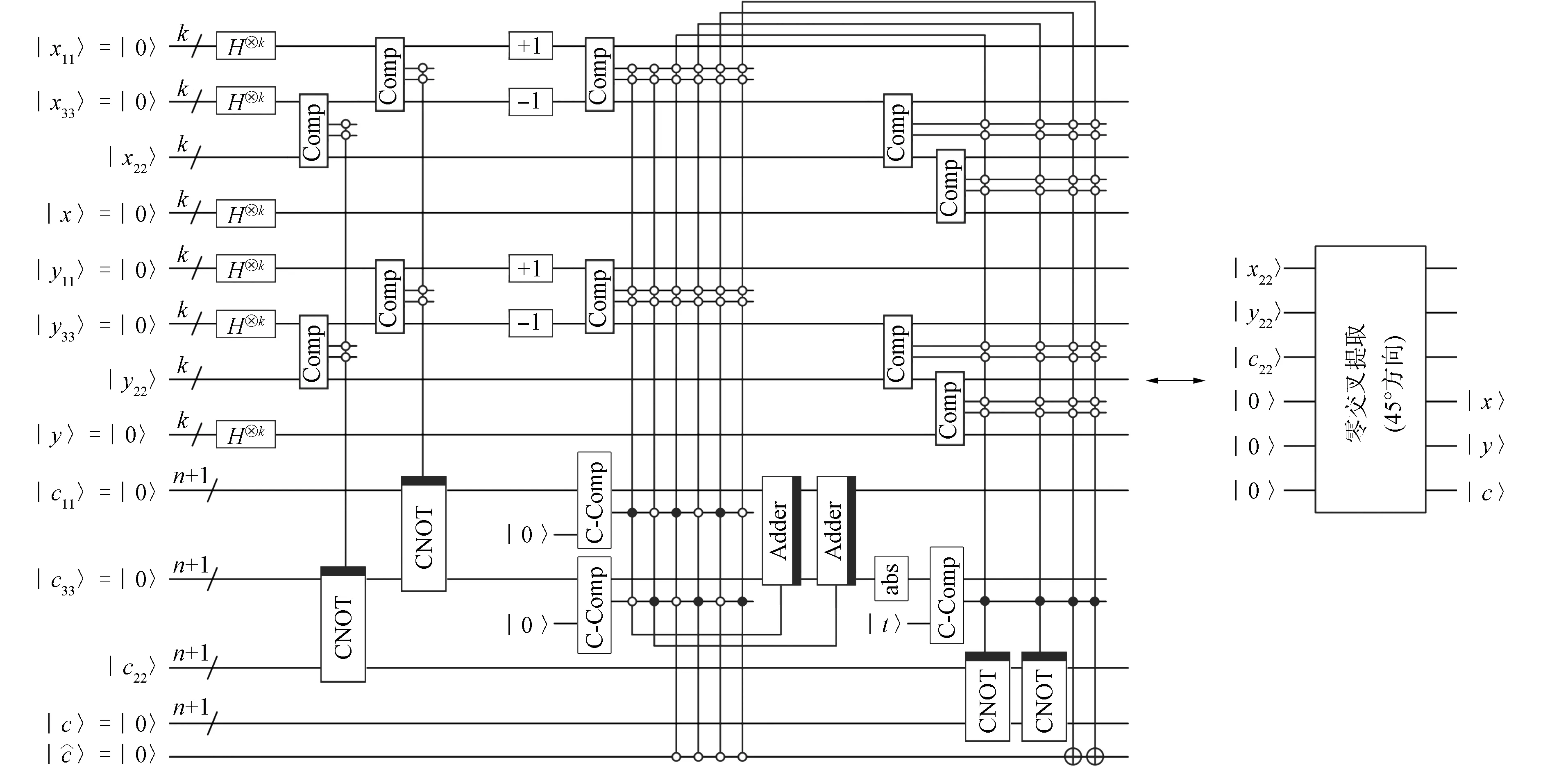
比较器在量子Marr-Hildreth边缘检测中具有重要作用, 其用于比较不同图像之间的像素位置, 具体量子线路可参见文献[26], 为简便, 本文采用如图2(A)所示的模块符号表示, 其中x和y是两个nbit输入数,e1e0是输出比特.若e1e0=10, 则x>y; 若e1e0=01, 则x 图2 比较器、 模加1和模减1量子线路的模块符号Fig.2 Module symbols of quantum circuits of comparator, modulo plus 1 and minus 1 本文所用的两个循环移位模块, 对于n位无符号整数x, 分别实现模加1和模减1.对(n+1)位的有符号数x=xm,xm-1…x0.x-1…xm-n, 分别实现x+2m-nmod 2m以及x-2m-nmod 2m.这两个模块的符号分别如图2(B)和图2(C)所示, 具体量子线路设计可参见文献[27]. 2.1.1 复制模块 该模块的功能是将一个nbit量子态复制到另一个nbit量子态|0〉⊗n, 显然可以用n个受控非门实现.具体的量子线路如图3所示.由图3可见, 在该模块的符号中, 不变的输入和输出用实心条标注.该模块将用于LoG滤波和零交叉提取. 图3 复制模块的量子线路Fig.3 Quantum circuits of copy module 2.1.2 翻转加1模块 该模块计算(n+1)位有符号数的相反数.设x=xm,xm-1…x0.x-1…xm-n为(n+1)位有符号数, 该模块首先对x中的所有量子比特进行翻转, 然后对翻转后的量子比特实施模加1.量子线路如图4所示.该模块将用于设计补码比较器和补码乘法器. 图4 翻转加1模块的量子线路Fig.4 Quantum circuits of flip and plus 1 2.1.3 右移模块 该模块将1个(n+1)位有符数x=xm,xm-1…x0.x-1…xm-n向右移动1个比特位, 使其成为(n+2)位的有符号数: (6) 由式(6)可知, 该模块也可称为减半模块, 该模块在两个有符号数的乘法线路设计中具有重要作用, 其量子线路如图5所示. 图5 右移模块量子线路Fig.5 Quantum circuits of right shift module 2.1.4 绝对值模块 该模块计算绝对值|x|, 其中x=xm,xm-1…x0.x-1…xm-n,xm是符号位, 该模块在零交叉提取中具有重要作用, 其量子线路如图6所示. 图6 绝对值模块量子线路Fig.6 Quantum circuits of absolute value module 2.1.5 模加法器模块 加法包括模加法和非模加法, 如果加法的结果小于模, 则这两种加法等价.对于两个(n+1)位有符号数的加法, 如果加法的结果超过模, 则通过使用(n+2)位表示这两个数, 这两个加法仍然等价.设两个(n+1)位有符号数分别为x=xm,xm-1…x0.x-1…xm-n,y=ym,ym-1…y0.y-1…ym-n, 且|x|<2m-1, |y|<2m-1.模加法量子线路如图7所示.该模块在LoG滤波和零交叉提取中具有重要作用. 图7 量子模加法器的量子线路Fig.7 Quantum circuits of quantum modulo adder 2.1.6 补码比较器模块 图2(A)中的比较器只能比较两个无符号的整数, 对于两个(n+1)位有符号数的比较, 可使用补码比较器, 其量子线路如图8所示.由图8可见, 首先, 利用复制模块将|y〉复制给辅助比特, 并应用翻转加1模块将其转换为|-y〉; 然后, 将|x〉和|-y〉提交给模加法器的输入, 在其输出端可得到; 最后, 检查辅助比特|e〉的状态, 当e=1时,x≥y, 否则x 图8 补码比较器的量子线路Fig.8 Quantum circuits of complement comparator 2.1.7 补码乘法器模块 补码乘法器是以基本的量子加法器等为基础, 设计快速高效的乘法器具有重要意义[28].设x=xm,xm-1…x0.x-1…xm-n,y=ym,ym-1…y0.y-1…ym-n为两个(n+1)位有符号数的补码描述, 实现x×y的量子线路如图9所示.在该线路中, 乘积采用(2n+1)个比特描述, 包括1个符号位, 2m个整数位和2(n-m)个小数位.该模块在LoG滤波中具有重要作用. 图9 两个有符号数补码乘法器的量子线路Fig.9 Quantum circuits of complement multiplier for two signed numbers 2.2 Marr-Hildreth边缘检测的量子线路设计 与经典的数字图像处理类似, 量子Marr-Hildreth边缘检测包括输入图像的LoG滤波和滤波后图像的零交叉提取两个步骤. 为避免卷积运算, 本文采用一种称为“移位、 叠加、 加权求和”的方法对量子图像进行LoG滤波. 首先, 将输入的原始图像在8个方向(即上左、 上、 上右、 左、 右、 下左、 下、 下右)移位一个单位或多个单位(取决于滤波罩的大小); 其次, 将移位后的图像和原始图像按照固定的顺序进行叠加, 在这些叠加的图像中, 相同位置的像素即为原始图像中被滤波罩覆盖的像素; 最后, 以滤波罩中对应的值为权重, 计算这些位置相同像素的加权和, 该加权和即为原始图像中相应像素的滤波结果. 这种方法的优点是借助量子计算的并行性, 可同时处理叠加图像中相同位置的所有像素, 从而达到加速经典计算的目的. 2.2.1 输入图像的LoG滤波 图10 一个5×5的LoG滤波罩及输入图像在各方向上的移位Fig.10 LoG filtering mask of 5×5 and input image translation in all directions 根据“移位、 叠加、 加权求和”的原理, 本文以3×3的滤波罩为例, 设计实现LoG滤波的量子线路如图11所示. 其中|I11〉表示大小为2k×2k的输入图像, 灰度值由(n+1)位有符号数的二进制补码表示, 包括一个符号比特和n个数据比特, 整个线路可分为三部分. 第一部分如第一个虚线框中的线路所示, 用于生成与输入图像(即|I11〉)完全相同的8张图像(即|I12〉,|I13〉,|I21〉,|I22〉,|I23〉,|I31〉,|I32〉,|I33〉).第二部分如第二个虚线框的线路所示, 它将第一部分产生的8张图像分别向8个方向平移, 该操作采用模加1和模减1模块实现.第三部分如第三个虚线框中的线路所示, 它将第二部分中生成的8张移位图像进行叠加, 并进一步计算叠加图像中相同位置像素的加权和, 从而实现LoG滤波. 首先, 用16个比较器确定堆叠图像中相同位置的像素, 然后用9个补码乘法器将每个像素|cij〉(i,j=1,2,3)乘以对应的|bij〉(i,j=1,2,3), 最后通过8个加法器实现加权求和. 图11 实现LoG滤波的量子线路Fig.11 Quantum circuits for LoG filtering 2.2.2 零交叉提取 与经典方法类似, 量子零交叉提取也考察4个方向.以45°方向的零交叉提取为例, 具体的量子线路如图12所示, 其余3个方向的量子线路基本相同.下面以图12中的量子线路为例, 简述零交叉提取的执行过程.|I22〉(|x22〉,|y22〉,|c22〉)为输入图像. 图12 45°方向的零交叉提取Fig.12 Zero-crossing extraction in 45° direction 其次, 用模加1模块将图像|I11〉向右下方分别移动1个单位, 用模减1模块将图像|I33〉向左上方分别移动1个单位.此时, 在输入图像|I22〉和两个移位图像|I11〉和|I33〉中, 同一位置的3个像素恰好是|I22〉输入图像中45°方向的3个像素.然后使用补码比较器比较|I11〉和|I33〉中同一位置的像素灰度值, 如果它们的符号相反, 则使用两个模加法器进一步计算两个灰度值之和S. 图13 Marr-Hildreth边缘检测的整体框架Fig.13 General framework for Marr-Hildreth edge detection 以下分析都基于一个2k×2k的灰度图像, 共(2k+23)个比特.在量子图像处理中, 线路网络的复杂度取决于所使用的基本门数量[30], 包括非门、 Hadamard门、 受控非门以及任何2×2的酉算子, 且基本量子门的复杂度为1.通过分析各子模块的复杂度, 逐步得到整个量子线路的复杂度. 在本文设计的所有线路中, 只有比较器、 模加1和模减1模块对像素位置比特进行操作, 其复杂度取决于图像的大小.其他模块工作在灰度值上, 与图像大小无关.由文献[26]可知, 量子比较器的复杂度不超过O(k2); 由文献[20]可知, 模加1和模减1的复杂度也不超过O(k2).对于大小为S×S的LoG滤波罩, 对应线路包含2(S2-1)k个Hadamard门、 4(S2-1)个比较器, 0.5(S3-S)个模加1和模减1模块、 (S2-1)个复制模块、 (S2-1)个补码乘法器和(S2-1)个模加法器.因此, LoG滤波线路的复杂度不超过O(k2). 由图12可见, 4个零交叉提取线路中共使用了40个比较器和12个模加1和模减1模块, 故零交叉提取的复杂度为O(40k2+12k2)=O(k2).因此, 本文设计的量子Marr-Hildreth边缘检测方案的复杂度不超过O(k2).对于经典Marr-Hildreth边缘检测方案, Gauss-Laplace滤波需要计算逐个像素, 其复杂度显然不低于O(22k).因此本文方法实现了对经典方法的指数加速. 由于目前量子计算机的硬件实现尚处于理论探索阶段, 所以本文仿真只能在经典计算机上进行. 虽然不能验证量子计算的并行性, 但能验证方案的执行效果. 所有仿真均在配置Inter(R)Core(TM)i7-10700CPU@2.90 GHz, 8.00 GB内存和64位操作系统的台式计算机上进行, 软件采用MATLAB(R2014b). 实验使用的4张灰度图像如图14所示. 图14 实验采用的4张原始图像Fig.14 Four original images used in experiment 第1张图片大小为233×233, 第2张和第3张图片大小为512×512, 最后一张图片大小为1 024×1 024. 本文中图像均采用文献[6]提出的NEQR模型表示, 图像大小必须满足2n×2n. 为使第1张图像满足此要求, 分别在图像底部和右侧增加23行和23列, 将图像扩展为256×256, 并将新增加的像素值全部设为零. 图15 实验用到的两个Gauss-Laplace滤波罩Fig.15 Two Gauss-Laplace filtering masks used in experiment 为考察量子Marr-Hildreth边缘检测的处理效果, 将本文方案与经典方案及文献[24]中的方案进行对比. 为保证比较结果的公平性, 经典方案也使用图15所示的两个滤波罩. 在零交叉提取中, 将最大灰度值的5%设定为3种方案的阈值. 对于4张输入图像, 3种方案的边缘检测效果对比结果如图16所示. 由图16可见, 本文方案和经典方案的结果相似, 肉眼分辨不出差别, 但在文献[24]方案的检测结果中, 图像的边缘有轻微噪声. 产生以上实验结果的原因如下: 图16 3种检测方案的实际效果比较Fig.16 Comparison of actual effects of three detection schemes 首先, 比较本文方案和经典方案, 二者检测原理几乎相同, 仅在边界像素的处理方式上略有差异, 本文方案采用“移位和堆叠”方法, 而经典方案采用将边界像素向外扩展的方法, 即当滤波罩中心位于边界像素时, 滤波罩内缺失的像素按边界像素处理. 由于边界像素的数量远小于整个图像的数量, 所以检测结果的差异肉眼几乎无法判别. 其次, 本文方案和文献[24]方案的边缘检测原理不同, 在文献[24]方案中, 首先使用Laplace算子对图像进行滤波, 然后计算滤波后图像中每个像素上灰度值的二阶差分, 最后在二阶差分图像中寻找零交叉像素. 这两种方案的区别在于图像预处理的方法不同, 本文LoG算子是Laplace算子和Gauss算子的组合, Gauss算子的功能是对图像进行平滑处理, 有助于去除图像中的高频噪声, 获得更清晰的图像边缘. 文献[24]方案采用具有锐化作用的Laplace算子, 其对去除图像高频噪声意义不大, 因此两个方案检测的效果略有不同. 根据上述实验结果, 量子方案检测效果与经典方案接近. 但本文方案的主要贡献不是提高检测效果, 而是提高计算效率. 利用量子计算固有的并行性, 本文方案能实现对经典方案的指数级加速. 下面通过在量子图像中混入量子比特翻转噪声, 考察噪声环境下量子图像的边缘检测效果. 量子比特翻转噪声本质上是一种信道噪声, 是信息在量子信道中传输时产生的. 它与经典信道噪声相似, 即在发送0时收到1, 或在发送1时收到0. 对于在信道中传输的量子图像, 量子比特翻转噪声将量子比特的状态在|0〉和|1〉之间翻转. 本文实验将翻转概率设为0.1, 图14中4张图像的噪声版本与其边缘检测效果如图17所示. 由图17可见, 虽然噪声图像非常模糊, 但边缘检测效果在视觉上没有变化, 表明该方案对噪声不敏感. 本文方案之所以能抵抗噪声, 是因为使用的LoG滤波器本质上是Gauss滤波器和Laplace算子的融合, 而Gauss滤波器具有低通平滑的功能, 可在一定程度上滤除混入的噪声. 图17 加噪图像以及对应的边缘检测结果Fig.17 Noisy images and corresponding edge detection effects 综上所述, 本文设计了经典Marr-Hildreth边缘检测的量子版本, 给出了实现LoG滤波和零交叉提取的完整量子线路. 经典计算机上的仿真实验验证了本文方案的有效性. 尽管该方案在检测效果上与经典方案差别较小, 但该方案的优势在于其计算效率. 复杂度分析结果表明, 该方案可实现对经典方案的指数级加速. 此外, 本文方案对量子信道噪声不敏感, 从而增强了方案的鲁棒性.
1.5 模加1和模减1模块
2 量子Marr-Hildreth边缘检测方法
2.1 一些辅助模块的量子线路设计













2.3 复杂性分析
3 经典计算机上的仿真



3.1 不同边缘检测方案性能对比

3.2 量子比特翻转噪声下的边缘检测效果

