美式Kou型跳扩散期权模型的Crank-Nicolson拟合有限体积法

江忠东, 甘小艇

(楚雄师范学院 数学与计算机科学学院, 云南 楚雄 675000)

随着金融市场的不断发展和完善, 期权作为一种能有效规避风险的金融工具越来越受到投资者和研究者们的广泛关注. 研究表明, 跳扩散期权定价模型所隐含的波动率曲线与市场实际观察到的波动率微笑十分接近, 很好地克服了标准Black-Scholes定价模型的缺陷[1]. 目前, 针对跳扩散期权定价模型的核心问题, 即数值定价的研究已取得了一系列成果[2-8]. Company等[9]提出了一种指数时间差分(FF-ETD)方法; 针对非光滑收益函数的存在, Wang等[10]给出了一个具有可变空间步长和可变时间步长的隐式-显式中点公式; Boen等[11]讨论了两资产Merton跳扩散模型下彩虹期权的数值解; Chen[12]研究了求解机制转换下亚式跳扩散期权的隐式-显式(IMEX)有限差分格式; 文献[13-14]针对跳扩散期权模型的定价, 讨论了一类全离散拟合有限体积格式的求解.

文献[13]针对美式Kou型跳扩散期权讨论了拟合有限体积法的求解, 但其中Crank-Nicolson格式的构造相对复杂, 且不利于进行理论分析. 基于此, 本文主要研究美式Kou型跳扩散期权模型一种修正的Crank-Nicolson拟合有限体积法求解, 并给出其收敛性证明. 此外, 本文还设计了求解非线性代数系统的一个迭代算法, 并证明其收敛性. 最后, 通过两个数值算例验证新方法的收敛性、 稳健性和有效性.

1 Crank-Nicolson拟合有限体积格式

考虑美式Kou型跳扩散期权定价模型, 假设标的资产价格S满足如下随机微分方程[2]:

(1)

其中:μ和σ分别表示资产价格未发生跳跃时的期望收益率和波动率;W(t)表示标准的Brown运动;N(t)表示强度为λ的Poisson过程; {Vi}表示一系列独立同分布的随机变量集合, 并且服从对数双指数密度分布:

(2)

式中α1>1,p,q,α2为正常数, 且满足p+q=1.

由文献[2]可知, 假设期权函数为V(S,τ), 令τ=T-t, 其中t和T分别为当前时间和到期日, 则美式Kou型跳扩散期权定价模型可表示为如下偏积分-微分互补问题:

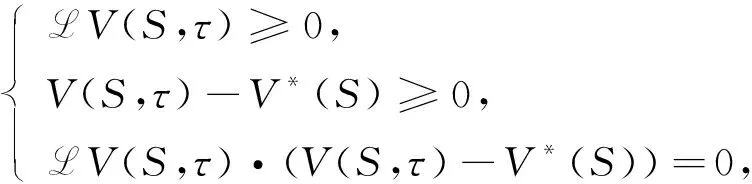
(3)

算子L满足

(4)

其中(S,τ)∈(0,+∞)×(0,T],r为无风险利率.考察美式看跌期权, 相应的初始条件为

V(S,0)=V*(S)=max{K-S,0},

(5)

边界条件为

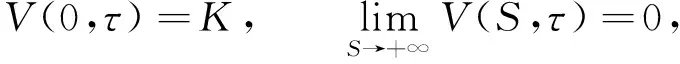
(6)

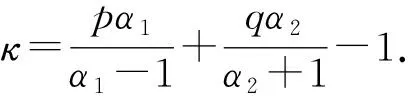
为数值求解上述期权定价问题, 需将变量S限制在有限的求解区域I=[0,Smax]上, 其中Smax的选取要足够大.此时, 边界条件(6)可变为

V(0,τ)=K,V(Smax,τ)=0.

(7)

本文采用罚方法逼近互补问题(3), 则可得如下非线性偏积分-微分方程:

LVγ(S,τ)-γ[V*-Vγ]+=0,

(8)

初始条件和边界条件分别为

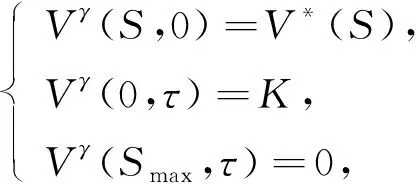
(9)

其中γ表示罚参数且γ>1, 对任何实数x满足[x]+=max{0,x}.

注1由于算子L的退化性, max{·,·}和收益函数的非光滑性和非线性性, 问题(3)和问题(8)-(9)通常没有经典的光滑解, 因此, 需寻找问题(3)和问题(8)-(9)的黏性解(有金融意义的解).为简便, 下面省略罚问题(8)-(9)的解Vγ的上标γ, 但要清楚V是问题(8)-(9)的解, 而不是问题(3)的解.

在给出离散化格式前, 先将方程(8)转换为守恒形式:

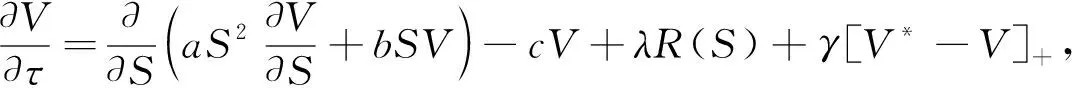
(10)

其中

拟合有限体积法的推导基于自共轭形式(10).首先, 给出区间I=[0,Smax]的两个空间分区.将I划分为J个子区间:

Ii=(Si,Si+1),i=0,1,…,J-1,

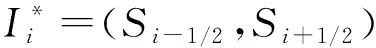
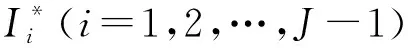
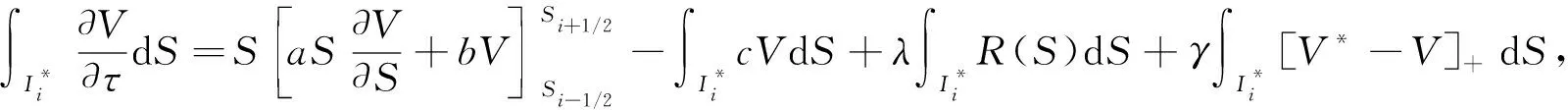
(11)

对式(11)所有的项应用矩形数值积分规则, 可得

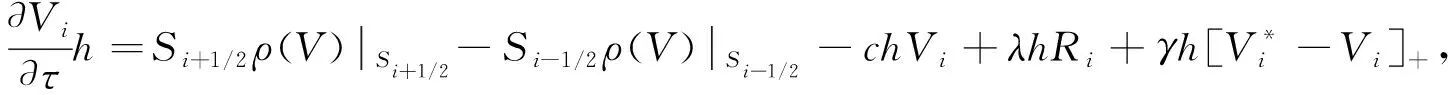
(12)

其中:Vi表示V(Si,τ)在空间离散点上的近似;ρ(V)称为连续通量, 定义为

ρ(V)∶=aSV′+bV;

(13)

Ri表示积分项R(S)在空间离散点上的逼近, 这里主要采用文献[2]中的线性插值技术和递推公式逼近积分项-λR(S), 并记所得离散矩阵为R.对R(S)的被积函数, 令y=z/S, 并对分段积分采用线性插值逼近, 则可得Ri的表达式为

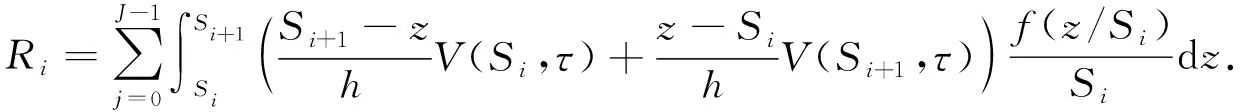
(14)

引理1[2]矩阵R+λI(λ>0)是一个具有非负对角元且对角占优的Z矩阵, 即

其中I为单位向量.

在单元Ii中点处, 关于连续通量ρ(V)的逼近参见文献[15].由文献[13]可知, 方程(10)半离散拟合有限体积法的矩阵形式为

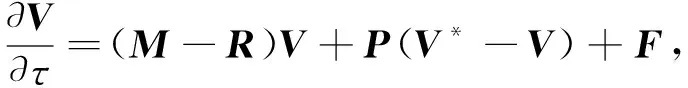
(15)

当i=1时, 有

当i=2,3,…,J-1时, 有

式中ξ=b/a,βi≥0,wi≥0,χi≤0且满足

-βi-χi-wi=r+λ>0.

(16)

下面构造方程(15)一种修正的Crank-Nicolson时间离散格式.对时间区间[0,T]做均匀网格剖分: 0=τ0<τ1<…<τN=T, 时间网格步长为Δτ=T/N, 则方程(15)修正的Crank-Nicolson拟合有限体积格式的矩阵形式为

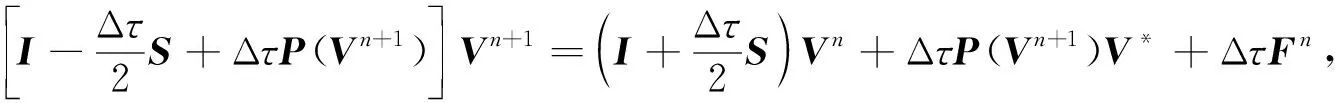
(17)

其中I为单位向量,S=M-R,V0=V*, 罚函数项对应的元素为

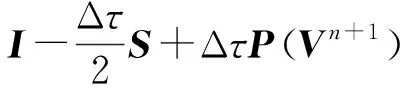
2 数值格式的收敛性

首先, 由文献[3]可知连续通量ρ(V)具有一致性, 因此显然如下结论成立.

引理2数值格式(17)是一致的.

其次, 证明数值格式(17)的稳定性.

引理3当Δτ→0时, 数值格式(17)是稳定的, 即

‖Vn‖∞≤‖V*‖∞,n=1,2,…,N.

证明: 将式(17)写成分量形式为

其中Rij≤0(i≠j).由式(18)和βi≥0,wi≥0,χi≤0, 对所有的i有

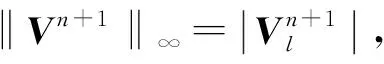
从而有

由-S的M矩阵性质及矩阵元素间的关系, 有

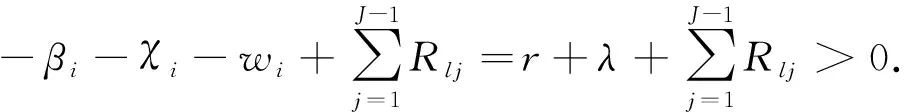
‖Vn+1‖∞≤max{‖Vn‖∞,‖V*‖∞}≤…≤max{‖V0‖∞,‖V*‖∞}=‖V*‖∞.

(20)

因此, 数值格式(17)是稳定的.证毕.

最后, 证明数值格式(17)是单调的.

引理4当Δτ→0时, 数值格式(17)是单调的, 即对任意的ε>0, 有

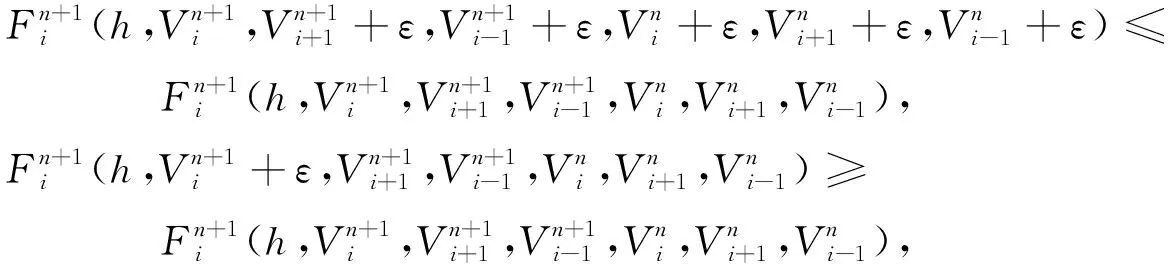
(21)

其中i=0,1,2,…,J, 数值格式(17)在每个离散点的形式为

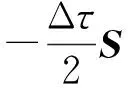
定理1当h→0时, 数值格式(17)求得的数值解收敛至罚问题(8)-(9)的黏性解.

证明: 由引理2～引理4可知, 数值格式(17)满足一致性、 稳定性和单调性, 从而由文献[16]可知, 当h→0时, 数值格式(17)求得的数值解必收敛至罚问题(8)-(9)的黏性解.证毕.

3 离散系统的迭代格式及其收敛性

由于P(Vn+1)项的存在, 因此数值格式(17)为非线性的代数系统, 为有效求解该代数系统, 下面给出相应的迭代算法并证明其收敛性.

算法1代数系统(17)的迭代算法.

步骤1) 置n=0;

步骤3) 求解

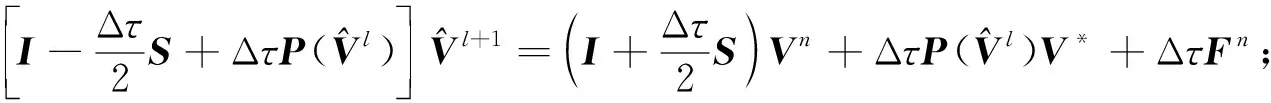
(23)

下面证明算法1的收敛性.

如引理3的证明, 式(24)可变为

采用与引理3相似的证明方法, 当Δτ→0时, 可得

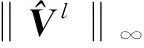
(25)

式(25)可化为

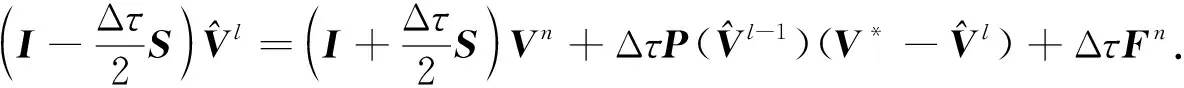
(26)

将式(23)减去式(26), 可得

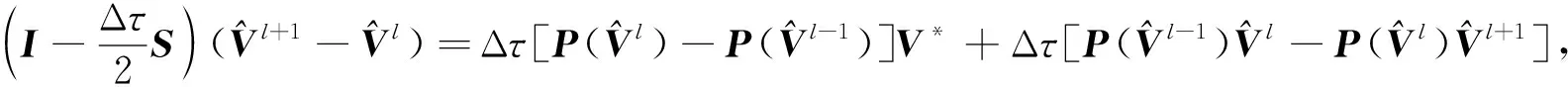
(27)

式(27)可化为

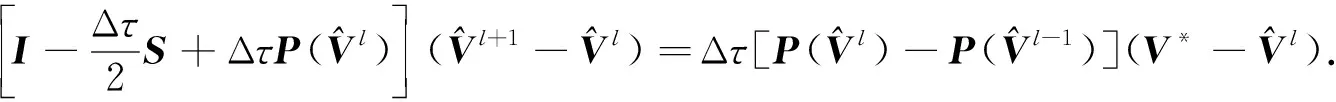
(28)

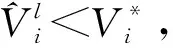
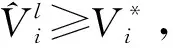
从而有

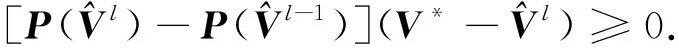
(29)

结合式(28),(29), 可得

(30)

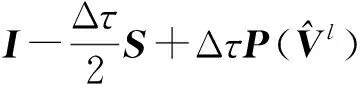
下面考察解的唯一性.假设式(23)有两个解B1和B2, 即满足

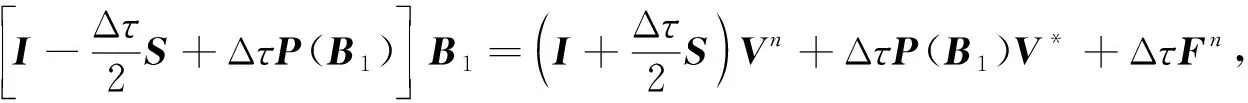
(31)

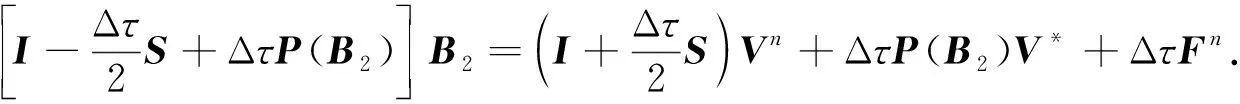
(32)

将式(31)减去式(32), 可得

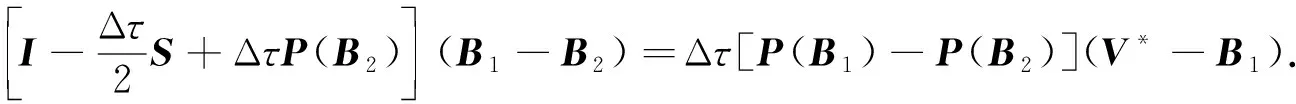
(33)

与证明式(30)成立同理, 可得

[P(B1)-P(B2)](V*-B1)≥0.

(34)

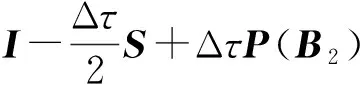
B1≥B2.

此外由对称性, 有

B2≥B1,

因此B1=B2.证毕.

注3定理2给出了算法1的解单调收敛至式(17)的唯一解.此外, 本文已证明了式(17)的解收敛到罚问题(8)-(9)的黏性解.因此, 算法1的解收敛至方程(8)-(9)的具有金融意义的解.

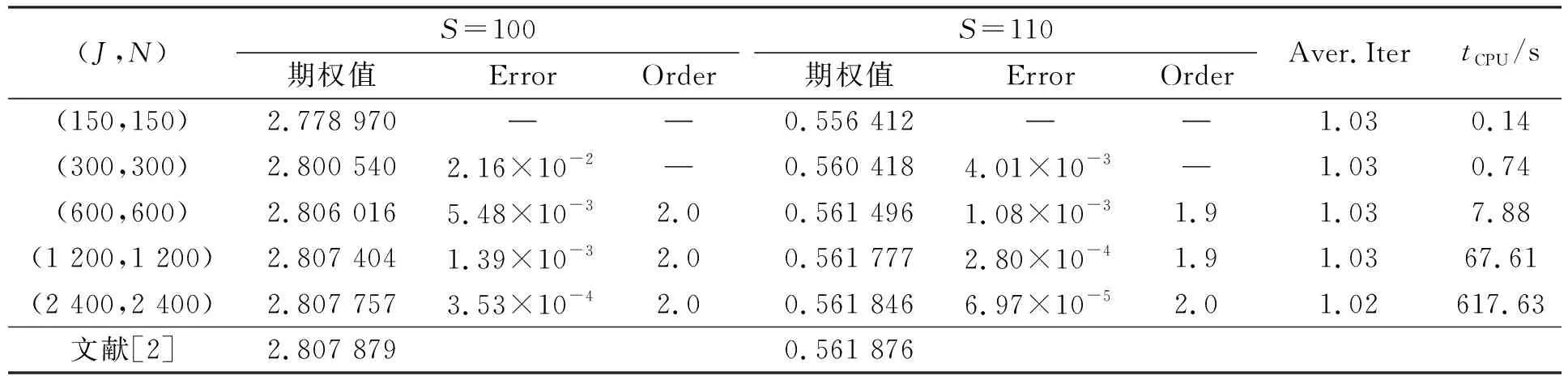
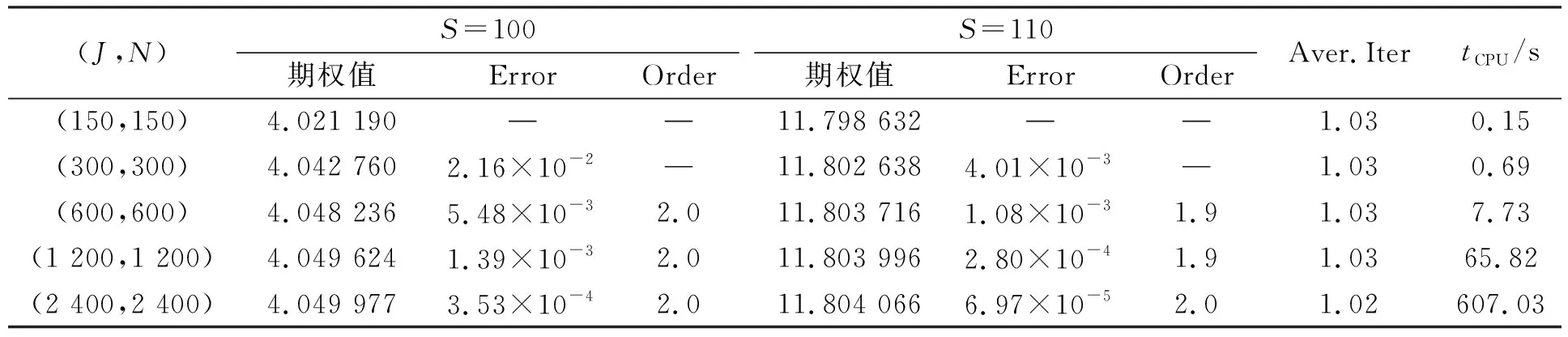
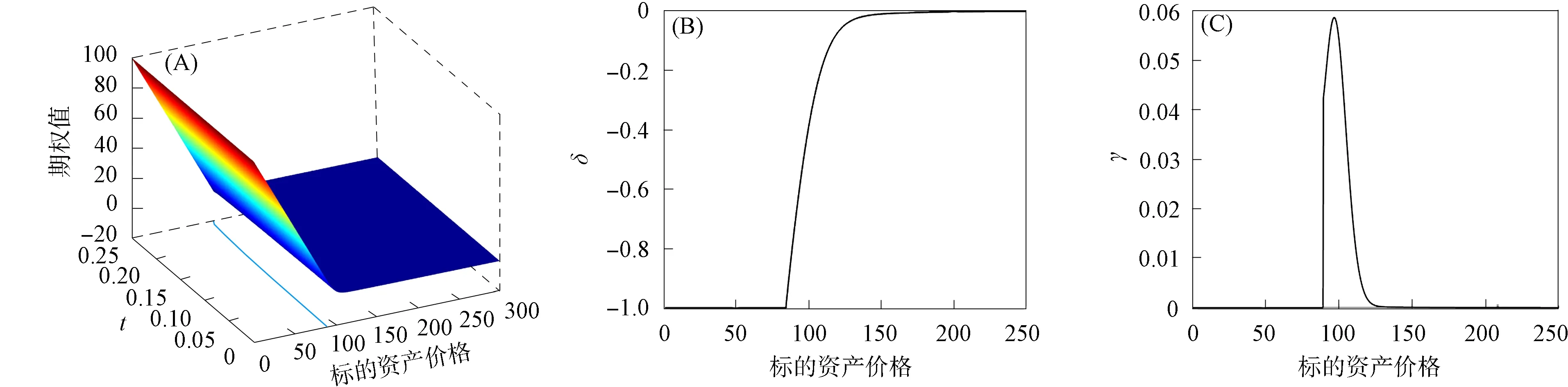
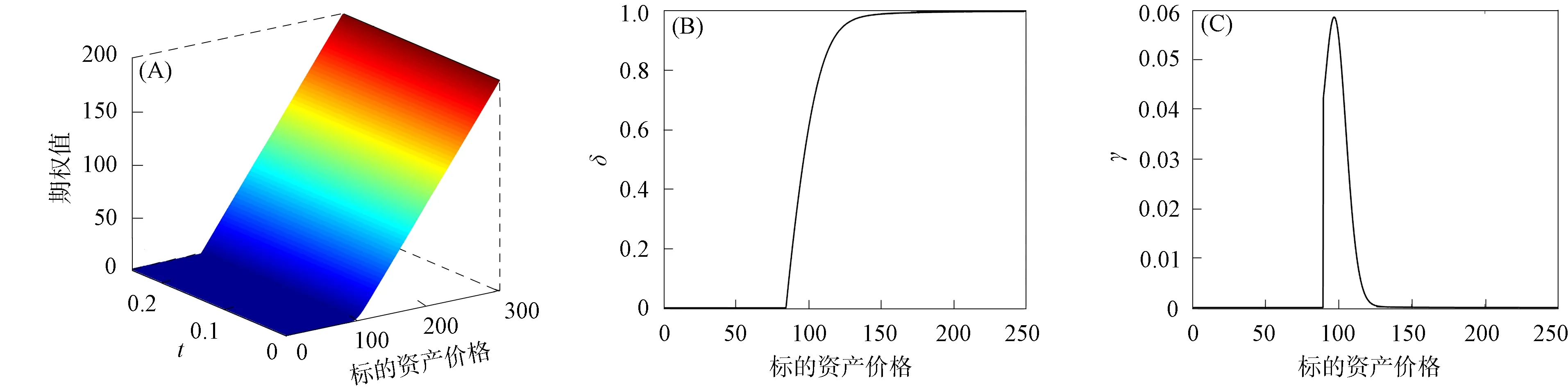
4 数值实验

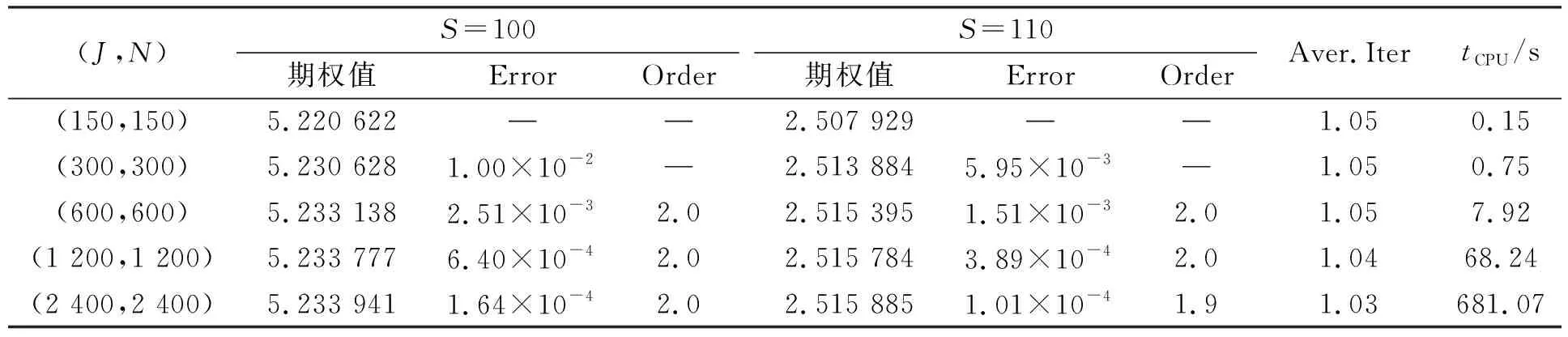
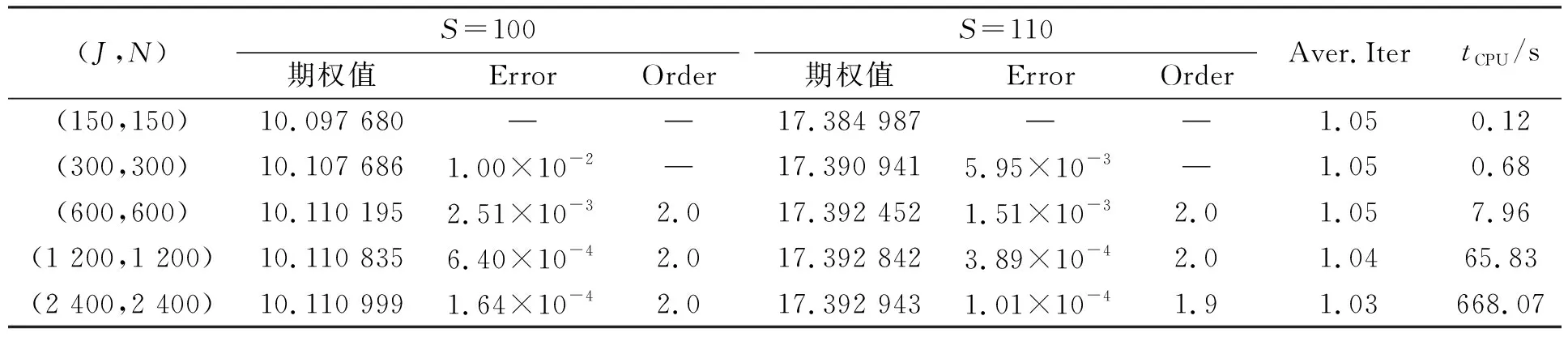
下面利用数值实验验证本文方法的有效性.实验中, 算法1中的罚参数γ和误差tolerance(tol)分别取106和10-6.为验证数值格式的收敛阶, 定义

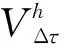
Order=log2R.

此外, 看涨期权的期权值可由如下平价公式计算得到:

Vc=Vp+S-Ke-rT,

(35)

其中Vc和Vp分别表示美式跳扩散期权在τ=T时刻的期权函数值.

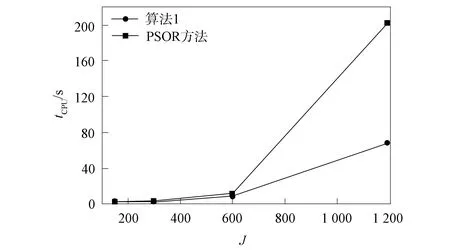
为说明本文方法的高效性, 将算法1与求解线性互补问题常用的投影超松弛迭代(projected successive overrelation, PSOR)方法[17]进行比较. 首先, 采用Crank-Nicolson拟合有限体积法离散美式Kou型跳扩散期权定价问题, 可得如下一系列时间层上的线性互补问题:

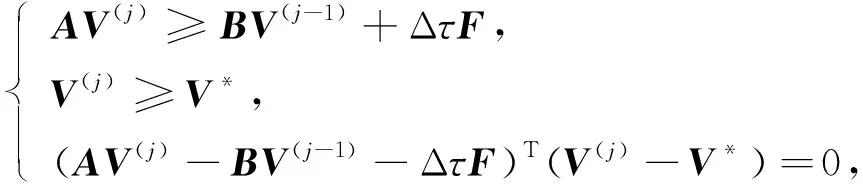
(36)

其中j=1,2,…,N, Δτ=T/N,V0=V*, 且

其次, 在线性互补问题(36)中, 令z∶=V(j)-V*,q∶=AV*-BV(j-1)-ΔτF, 则可得标准的线性互补问题(简记为LCP(q,A)):

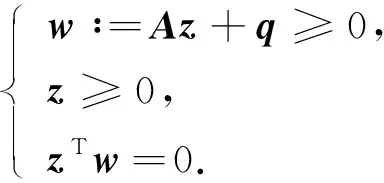
(37)

下面给出求解线性互补问题(37)的PSOR方法, 其中松弛因子α取使得CPU时间最小所对应的值, tol取10-6.

算法2PSOR方法.

步骤1) 给定J,α,tol,maxit;

步骤2) For it=1,2,…,maxit

步骤3) Fori=1,2,…,J

步骤4)k=(1,2,…,J);

步骤5)z(i)=z(i)+α(-q(i)-A(i,k)z(k))/A(i,i);

步骤6)z(i)=max{z(i),0};

步骤7) End For

步骤8) Res=‖min{Az+q,z}‖2;

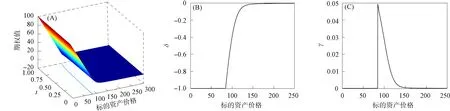
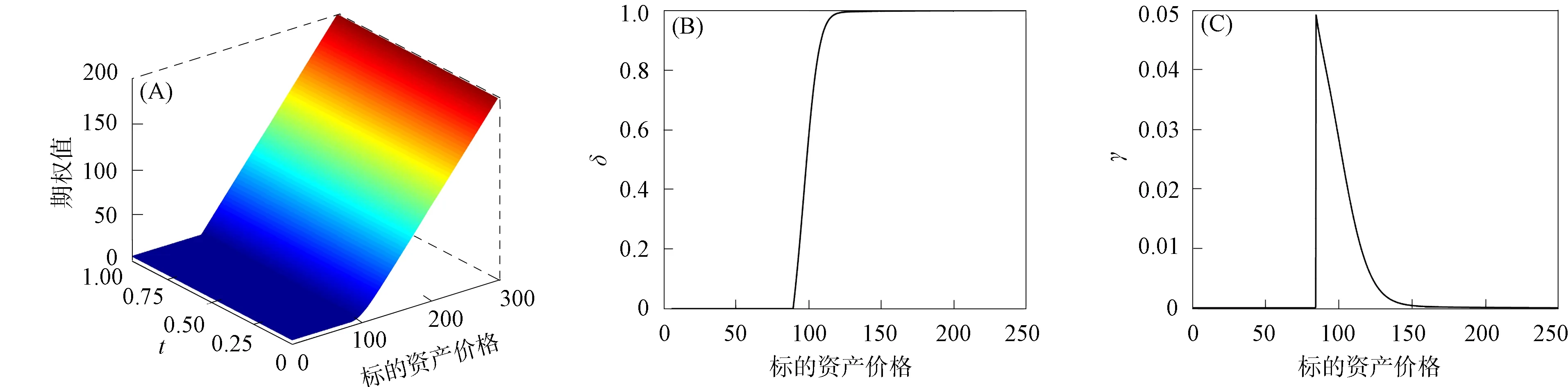
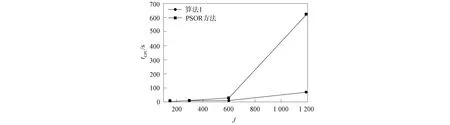
步骤9) If Res

步骤10) break;

步骤11) End If

步骤12) End For

下面所有的数值实验均在CPU为3.4 GHz、 内存为32 GB, 且编程环境为MATLAB R2015a的计算机上进行,J和N分别表示空间和时间方向的网格剖分数.

例1美式Kou型跳扩散期权的模型参数取为

σ=0.15,r=0.05,T=0.25,K=100,λ=0.1,

α1=3.046 5,α2=3.077 5,p=0.344 5,q=0.655 5,

截取Smax=3K, 则求解区域为(0,Smax)×(0,T).

例1的模型参数与文献[2,5]相同.

首先, 基于Crank-Nicolson拟合有限体积法并结合罚函数法的求解, 计算在τ=T时刻、S=100,110处美式Kou型跳扩散看跌和看涨期权的期权值、 期权值的连续变化情况(Error)、 收敛阶(Order)、 算法1下的平均迭代步数(Aver.Iter)和所需的CPU时间, 结果分别列于表1和表2. 由表1和表2可见： 所有期权值都呈现了清楚的收敛趋势, 且收敛阶为2阶(类似的验证方法可参见文献[14,18]); 在给定适当的精度水平下, 由Aver.Iter和CPU时间两列数值可见, 算法1求解非线性代数系统(17)是高效的.

表1 例1中Crank-Nicolson拟合有限体积法定价美式看跌期权的计算结果

表2 例1中Crank-Nicolson拟合有限体积法定价美式看涨期权的计算结果

其次, 基于网格剖分(J,N)=(2 400,2 400), 图1和图2分别给出了期权曲面、 最佳实施边界以及τ=T时刻的δ值和γ值. 由图1和图2可见, 数值解的性态优良, 未发生跳跃和震荡现象, 表明本文全离散格式是稳健的.

图1 例1中当网格剖分为(J,N)=(2 400,2 400)时, 看跌期权的价格曲面和最佳实施边界(A)及在τ=T时刻的δ值(B)和γ值(C)Fig.1 When grid is divided into (J,N)=(2 400,2 400), put option value surface and optimal implementation boundary (A), δ value (B) and γ value (C) at τ=T in example 1

图2 例1中当网格剖分为(J,N)=(2 400,2 400)时, 看涨期权的价格曲面和最佳实施边界(A)及在τ=T时刻的δ值(B)和γ值(C)Fig.2 When grid is divided into (J,N)=(2 400,2 400), call option value surface and optimal implementation boundary (A), δ value (B) and γ value (C) at τ=T in example 1

最后, 以看跌期权为例, 图3给出了当网格剖分为J=N时, 算法1和PSOR方法求解美式期权定价问题所需CPU时间的比较. 由图3可见, 随着网格的加密, 算法1所需的CPU时间小于PSOR方法.

图3 例1中当J=N时, 算法1与PSOR方法求解美式看跌期权的CPU时间Fig.3 CPU time of algorithm 1 and PSOR method for solving American put options when J=N in example 1

例2美式Kou型跳扩散期权的模型参数取为

σ=0.15,r=0.05,T=1,

K=100,λ=0.1,α1=3,α2=3,

p=0.333 333,q=0.666 667,

截取Smax=3K, 求解区域为(0,Smax)×(0,T).

例2的模型参数与文献[7]相同.

首先, 计算在τ=T时刻、S=100,110处美式Kou型跳扩散看跌和看涨期权的期权值、 Error、 Order、 以及算法1的Aver.Iter和CPU时间, 所得结果分别列于表3和表4. 由表3和表4可见, 期权值呈现了清晰的收敛趋势, 且数值格式的收敛阶为2阶, 该结果与通常情况下的Crank-Nicolson格式的性质相符. 此外, 由Aver.Iter和CPU时间可见, 算法1求解非线性代数系统(17)是高效的.

表3 例2中Crank-Nicolson拟合有限体积法定价美式看跌期权的计算结果

表4 例2中Crank-Nicolson拟合有限体积法定价美式看涨期权的计算结果

其次, 基于网格剖分(J,N)=(2 400,2 400), 图4和图5分别给出了期权曲面和最佳实施边界以及τ=T时刻的δ值和γ值. 由图4和图5可见, 数值解的性态十分优良, 未发生跳跃和震荡现象, 表明本文的Crank-Nicolson格式稳健.

图4 例2中当网格剖分为(J,N)=(2 400,2 400)时, 看跌期权的价格曲面 和最佳实施边界(A)及在τ=T时刻的δ值(B)和γ值(C)Fig.4 When grid is divided into (J,N)=(2 400,2 400), put option value surface and optimal implementation boundary (A), δ value (B) and γ value (C) at τ=T in example 2

图5 例2中当网格剖分为(J,N)=(2 400,2 400)时, 看涨期权的价格曲面 和最佳实施边界(A)及在τ=T时刻的δ值(B)和γ值(C)Fig.5 When grid is divided into (J,N)=(2 400,2 400), call option value surface and optimal implementation boundary (A), δ value (B) and γ value (C) at τ=T in example 2

最后, 与例1相似, 图6给出了例2中当J=N时, 算法1与PSOR方法求解美式看跌期权的CPU时间. 由图6可见, 算法1在求解美式期权定价问题所需的CPU时间远小于PSOR方法.

图6 例2中当J=N时, 算法1与PSOR方法求解美式看跌期权的CPU时间Fig.6 CPU time of algorithm 1 and PSOR method for solving American put options when J=N in example 2

综上所述, 本文研究了美式Kou型跳扩散期权定价模型的数值求解. 首先, 构造了定价方程的一种修正的Crank-Nicolson拟合有限体积格式, 并验证了其一致性、 稳定性和单调性, 因此数值格式求出的数值解收敛至相应的黏性解. 其次, 针对罚函数项离散导致的非线性代数系统数值求解困难问题, 设计了一个有效的迭代算法, 并验证了其收敛性. 最后, 给出两个数值算例验证本文方法是收敛、 高效且稳健的.