一类带p-Laplace算子的Caputo分数阶导数边值问题解的存在性
2022-07-07李小平
李 小 平
(湘南学院 数学与信息科学学院, 湖南 郴州 423000)
0 引 言
目前, 关于分数阶微积分方程的研究已取得了许多成果[1-9]. 文献[8]用单调迭代法研究了如下带p-Laplace算子分数阶微分方程四点边值问题正解的存在性:

(1)
其中:
Dα,Dβ,Dγ是标准的Riemann-Liouville分数阶导算子,f∈C([0,1]×[0,∞),[0,∞)).文献[9]利用Gronwall不等式和不动点定理, 研究了具有Riesz-Caputo导数的分数阶微分方程
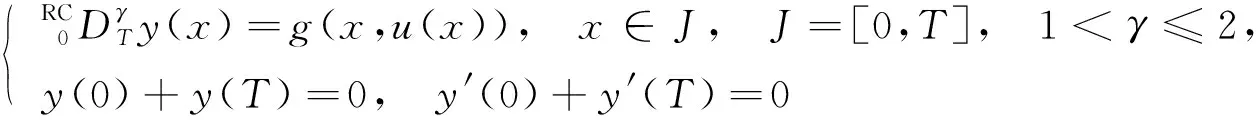
(2)

但目前关于带p-Laplace的Caputo分数阶导数的边值问题可解性研究文献报道较少, 基于此, 本文研究如下带p-Laplace的Caputo分数阶导数的边值问题解的存在性:

(3)

1 预备知识
定义1[10]函数f: (0,+∞)→的ζ>0阶Riemann-Liouville分数阶积分定义为
定义2[10]函数f: (0,+∞)→的ζ>0阶Caputo分数导数定义为
其中n=[ζ]+1, [ζ]表示实数ζ的整数部分.
引理1[10]设ζ>0,n=[ζ]+1, 则方程CDζf(t)=0的解为
f(t)=d0+d1t+d2t2+…+dn-1tn-1,
其中di∈,i=0,1,2,…,n-1.
引理2[10]设ζ>0,n=[ζ]+1, 则有
IζCDζf(t)=f(t)+d0+d1t+d2t2+…+dn-1tn-1,
其中di∈,i=0,1,2,…n-1.


(4)
的唯一解为

(5)
其中,

(6)
证明: 由引理2及方程(4), 可得
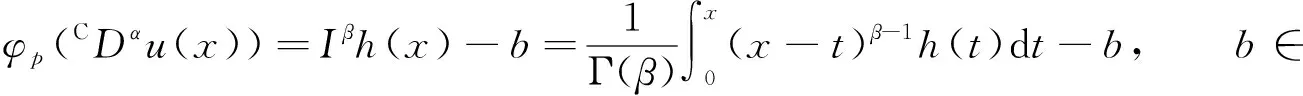
由CDαu(0)=0, 有b=0.从而有
φp(CDαu(t))=Iβh(x),
(7)

(8)
由引理2, 得等价的积分方程:
其中m1,m2,m3∈.
通过计算得
由u″(0)=0, 得m3=0.进一步由边值条件u(0)+u′(0)=0,u(1)+u′(ξ)=0, 可得
m1+m2=0,
则
所以
证毕.
引理4式(6)定义的G(x,t)满足如下性质:
1)G(x,t)∈C([0,1]×[0,1]),G(x,t)>0, ∀x,t∈(0,1);
2) 存在函数ν(t),ω(t)∈C(0,1), 使得


证明: 1) 由G(x,t)的定义易知1)成立.
2) 设
则可得
所以有

1) 当u∈K∩∂Z1时, ‖Tu‖≤‖u‖, 且u∈K∩∂Z2, ‖Tu‖≥‖u‖;
2) 当u∈K∩∂Z1时, ‖Tu‖≥‖u‖, 且u∈K∩∂Z2, ‖Tu‖≤‖u‖.


1) 当u∈K(θ,r2,r3)时, {u∈K(θ,r2,r3)|θ(u)>r2}≠0, 且θ(Tu)>r2;
2) 当u≤r1时, ‖Tu‖ 3) 当u∈K(θ,r2,r3)时, ‖Tu‖>r3,θ(Tu)>r2. 则T至少存在3个不动点u1,u2,u3, 其中‖u1‖ K={u∈X|u(x)≥0, 0≤x≤1}. 引理7算子T:K→X定义为 则算子T:K→K是全连续的. 证明: 函数G(x,t),f(x,u)是非负且连续的, 所以算子T:K→K是连续的, 由Arzela-Ascoli定理和Lebesgue控制收敛定理知算子T:K→K是全连续的. 为方便, 记 χ(h)=max{f(x,u),(x,u)∈[0,1]×[0,h]},ψ(h)=min{f(x,u),(x,u)∈[0,1]×[0,h]}. 定理1假设f: [0,1]×[0,+∞)→[0,+∞)是一个连续函数, 且存在两个正数τ1>τ2>0, 使得 χ(τ1)≤φp(τ1L),ψ(τ2)≥φp(τ2M), 则边值问题(3)至少有一个正解u满足τ2≤‖u‖≤τ1. 证明: 下面分两步进行证明. 1) 设Z1∶={u∈K|‖u‖≤τ1}.对于∀u∈∂Z1, 有‖u‖=τ1,f(x,u(x))≤χ(τ1)≤φp(τ1L), 其中(t,u)∈[0,1]×[0,τ1].则 因此, 对于∀u∈∂Z1, ‖Tu‖≤‖u‖. 2) 设Z2={u∈K|‖u‖≤τ2}.对于∀u∈∂Z2, 有‖u‖=τ2,f(x,u(x))≥ψ(τ2)≥φp(τ2M), 其中(x,u)∈[0,1]×[0,τ2].则有 定理2假设f∈C([0,1]×[0,+∞), [0,+∞)), 存在3个正数0<τ1<τ2<τ3, 使得: 1) 当(x,u)∈[0,1]×[0,τ1]时,f(x,u)≤φp(Lτ1); 2) 当(x,u)∈[1/4,3/4]×[τ2,τ3]时,f(x,u)≥φp(Mτ2); 3) 当(x,u)∈[0,1]×[0,τ3]时,f(x,u)≤φp(Lτ3). 则边值问题(3)至少有3个解u1,u2,u3, 满足: (10) (11) (12) 证明: 下面分四步证明. 且 {u∈K(θ,τ2,τ3)|θ(u)>τ2}≠Ø. 所以如果u∈K(θ,τ2,τ1), 则τ2≤u(t)≤τ3, 1/4≤t≤3/4.由假设2)知,f(x,u)≥φp(Mτ2),u∈K(θ,τ2,τ1), 从而 所以∀u∈K(θ,τ2,τ1), 有θ(Tu)>τ2, 即满足引理6的条件1). 即满足引理6的条件2). 4) 如果u∈K(θ,τ2,τ3), 则由2)有θ(Tu)>τ2, 即满足引理6的条件3). 由引理6, 边值问题(1)至少有3个非负解u1,u2,u3, 满足式(10)~(12). 例1考虑边值问题: (13) 例2考虑边值问题: (14) 其中 由定理2知, 边值问题(14)至少有3个非负解u1,u2,u3, 满足:2 主要结果









3 应用实例





