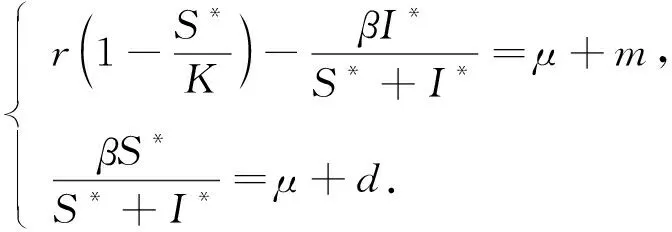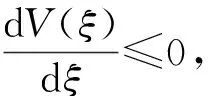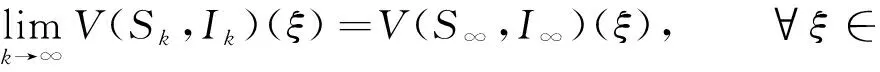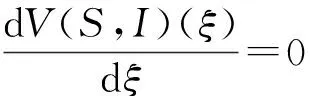不同扩散策略下SI传染病模型的行波解
2022-07-07焦战
焦 战
(山西大学 复杂系统研究所, 太原 030006)
0 引 言
传染病可通过构建数学模型提供可靠的信息, 从而进一步有效预防和控制疾病的传播. 假设一个地区内人口分为易感者和染病者, 并且在无染病者的情况下, 易感者人群的增长率通过Logistic模型表示, 因此Berezovsky等[1]提出了如下模型:
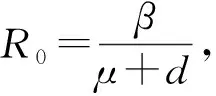
在许多情况下, 种群的空间变化在疾病传播模型中具有重要作用, 因此, 许多研究都将空间因素考虑在内[2-3].在人口生态学中, 非局部扩散比局部扩散可以更好地描述一个长期过程, 可通过积分算子描述扩散过程.但实际应用中会对易感者人群采取保护措施, 因此易感者将采用局部扩散策略, 染病者采用非局部扩散策略, 所以可得如下扩散SI传染病模型:
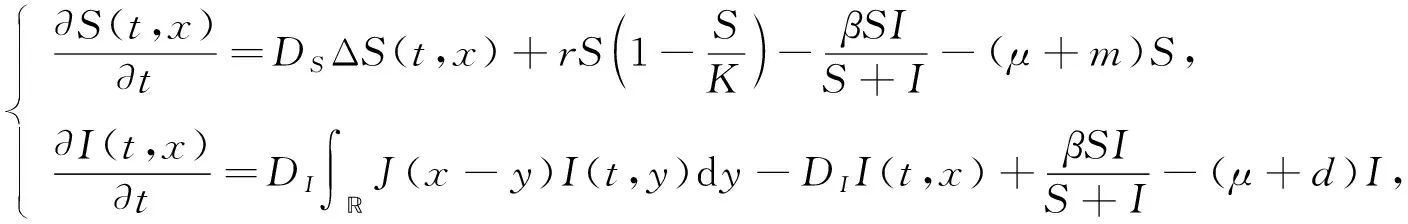
(1)
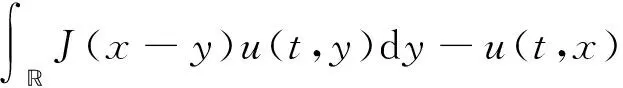
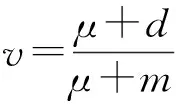
目前, 关于扩散流行病模型中行波解的研究得到广泛关注, 其可用于描述疾病以恒定速度在空间上传播的状态[5-7].在生物学背景下, 要讨论的问题之一是行波解是否存在.Diekmann[8]使用上下解方法证明了单调系统行波解的存在性; Dunbar[9]利用打靶法证明了非单调系统行波解的存在性; 文献[10-11]用Schauder不动点定理证明了非单调系统行波解的存在性; Wang等[12]使用Schauder不动点定理和Laplace变换, 研究了一类具有非局部时滞传播的扩散Kermack-Mckendrick流行病模型行波解的存在性和不存在性, 并建立了一些定理; Zhang等[13]研究河流中含对流的反应扩散捕食-食饵模型, 建立了上游和下游方向上捕食者入侵行波解, 并得到了最小波速及水文和生物因素对最小波速的影响. 本文进一步研究不同扩散策略下的SI传染病模型, 证明连接无病平衡点E0和地方病平衡点E1行波解的存在性、 有界性以及渐近行为.
1 预备知识
为研究系统(1)的行波解, 假设核函数J(x) 满足下列性质:
(H2)J(·)在中是Lipschitz连续的;
(H3)J具有紧支集.
对于系统(1)的行波解, 是指具有以下形式的特殊解:
(S(x,t),I(x,t))=(S(ξ),I(ξ)),
(2)
其中ξ=x+ct∈,c>0为波速.将式(2)代入系统(1)可得如下行波方程:

(3)
寻找系统(3)满足边界条件:
(S,I)(-∞)=(S0,I0), (S,I)(+∞)=(S*,I*)
(4)
的正解.将系统(3)的第二个方程在无病平衡点(S0,I0)处线性化可得
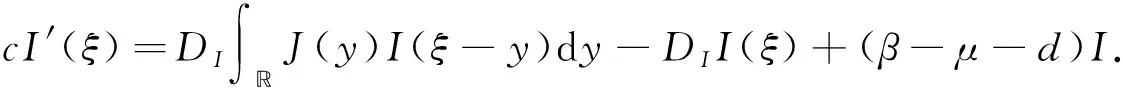
(5)
将I(ξ)=eλξ代入式(5), 可得如下特征方程:
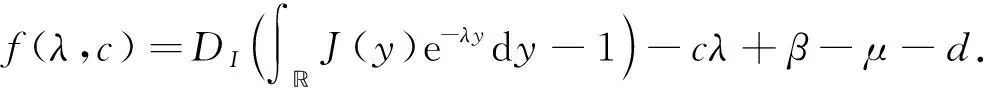
(6)
对任意的λ>0及c>0, 计算可得:
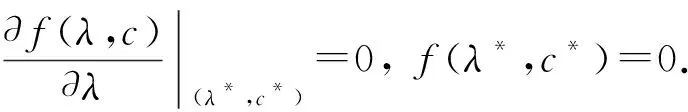
引理1假设R0>1,Rd>1, 且下列性质成立:
1) 如果c=c*, 则f(λ,c)=0有两个相同的实根λ*;
2) 如果0
3) 如果c>c*, 则f(λ,c)=0有两个不同的实根λ1(c),λ2(c), 且满足0<λ1(c)<λ*<λ2(c)<λ0, 以及
2 行波解的存在性
下面总假设R0>1,Rd>1,c>c*.定义如下连续函数:
其中σ,,η,M都是待定的正常数,λ1=λ1(c)在引理1中已给出.


(7)
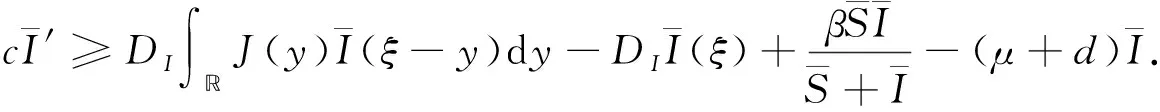
(8)
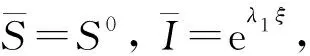
从而不等式(8)成立.证毕.
引理3对于充分小的0<函数满足
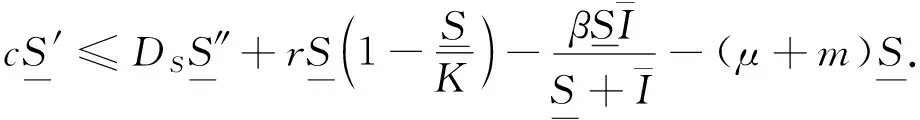
(9)
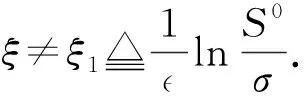
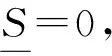
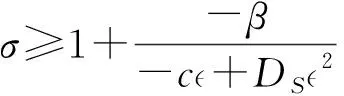
证毕.

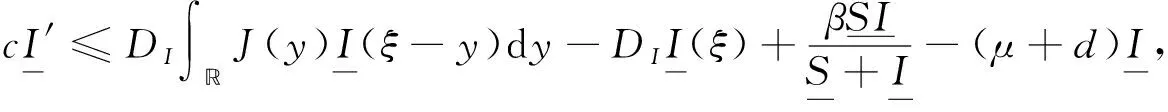
(10)
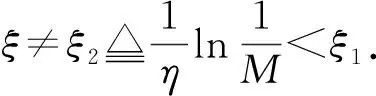
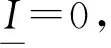
根据η<<λ1, 可得再根据引理1可知f(λ1+η,c)<0, 则
证毕.
令X>-ξ2, 定义集合
显然ΓX在C([-X,X],2)上是一个闭凸集.
对于给定的(φ(ξ),ψ(ξ))∈ΓX, 定义
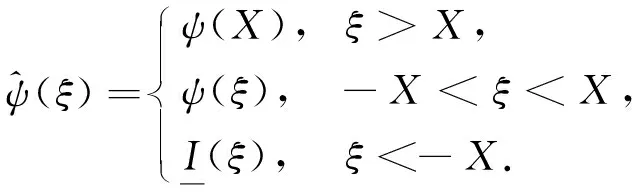
对任意的ξ∈[-X,X], 考虑下列初值问题:
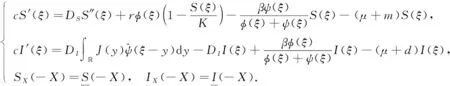
(11)
由泛函微分方程的基本理论[14]可知, 初值问题(11)有唯一解(SX(ξ),IX(ξ)), 且SX(·)∈W2,p,IX(·)∈C1([-X,X]), 其中p≥2.定义算子F=(F1,F2):ΓX→C([-X,X]), 其中
SX=F1(φ,ψ),IX=F2(φ,ψ).
引理5算子F=(F1,F2)将ΓX映射到其自身.
证明: 首先, 对∀(φ(·),ψ(·))∈ΓX, 需证
根据算子F的定义, 可得

引理6算子F=(F1,F2)是全连续的.
证明: 首先证明算子F的连续性.通过直接计算可得
其中
注意到对∀(φ1(·),ψ1(·)), (φ2(·),ψ2(·))∈ΓX, 有
从而hψ关于ψ连续, 根据式(12),(13)可知F连续.
其次证明算子F的紧性.因为
所以由标准椭圆估计、 嵌入定理可知算子F是紧的.进而可知算子F是全连续的.证毕.
应用Schauder不动点定理可知, 存在(SX,IX)∈ΓX满足
SX(ξ)=F1(SX,IX)(ξ),IX(ξ)=F2(SX,IX)(ξ), ∀ξ∈[-X,X].
为得到系统(3)行波解的存在性, 首先在下列空间中给出关于SX(·)和IX(·)的先验估计:
C1,1([-X,X])={u∈C1([-X,X])|u和u′是Lipschitz连续的},
且具有如下范数:
引理7对任意的X>-ξ2, 存在常数C(X)>0, 使得
‖SX‖C3([-X,X])≤C(X), ‖IX‖C1,1([-X,X])≤C(X).
证明: 因为(SX,IX)是算子F的不动点, 所以有
其中
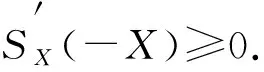
由式(16)可得
又由于
因此存在常数C1(X)>0, 使得‖SX‖C2([-X,X])≤C1(X).
令M1=max{S0,eλ1X}, 使得对∀ξ∈[-X,X], 有0≤SX(ξ)≤S0≤M1, 0≤IX(ξ)≤eλ1X≤M1, 因此
所以存在某个常数C2(X)>0, 使得‖IX‖C1([-X,X])≤C2(X).进一步有
|IX(ξ)-IX(ζ)| (17) 根据式(15)可得 由假设(H1)~(H3)知J在上具有紧支集且是Lipschitz连续的.取L为J的Lipschitz系数,R为J的支集半径, 则 且 (18) 下面证明I(ξ)在中有界. 引理8存在正常数C, 使得 所以 (19) 整理得 (20) 另一方面, 对式(19)两边同时从ξ-R0到ξ积分, 可得 因此有 W(ξ+R0)≤δ0W(ξ), (21) 进一步, 有 证毕. 引理9对于ck∈[c1,c2], 其中0 证明: 反证法.假设存在一列 {ξk}及实数>0, 使得当k→+∞时,Ik(ξk)→+∞且Sk(ξk)≥.由系统(3)中第一个方程及引理7可知, 存在正常数C4, 使得S″≤C4, 所以 (22) 对式(22)从ξ到ξk积分并应用Sk(ξk)≥, 可得 Sk(ξ)≥-δ1(ξk-ξ). 由于当k→+∞时,Ik(ξk)→+∞, 则当k→+∞时, 有 再根据系统(3)中第一个方程可知, 当k→+∞时, 有 因此存在一个k0>0, 使得当k≥k0时, 有 因为对任意的ξ∈, 均有Sk(ξ) 所以对任意的ξ∈[ηk-R,ηk+R], 有I(ξ)≥I0+1.因此[ηk-R,ηk+R]⊂[ξk,ξk+1].由系统(3)中第二个方程可得 引理11I(ξ)在中有界. 通过计算可得 由于 不妨假设对任意的k∈, 有ξk=0.选取子列{ck}k∈, 使得当k→+∞时, 有ck→c∞∈[c1,c2].则由引理8可知存在常数C6, 使得系统(3)以ck为波速的解(Sk,Ik)满足因为当k→+∞时有Ik(0)→0, 因此Ik在中局部一致收敛于0, 从而在中局部一致收敛于0.由于和局部有界, 故对于子列{ck}k∈, 当c=c∞时有0≤S∞≤S0,I∞=0, 且 (23) 令D=infS∞, 选取一列{ηk}k∈, 使得当k→+∞时有S∞(ηk)→D.抽取子列, 函数S∞(ξ+ηk)在中收敛到函数U∞, 使得在中有 对任意的k∈及ξ∈, 定义由于在L∞中有界,Zk局部有界, 所以局部有界, 再根据系统(3)中第二个方程可知也局部有界.由Arzela-Ascoli定理可知函数Zk在中收敛到Z∞(ξ), 且Z∞(ξ)满足 (24) 假设存在ξ0∈, 使得Z∞(ξ0)=0, 由式(24)有Z∞(ξ0-y)=Z∞(ξ0)=0, 表明Z∞=0恒成立, 与Z∞(0)=1矛盾.因此Z∞>0. (25) (26) 设W在ξ1∈处取得最小值, 则W′(ξ1)=0.由式(26)可得对∀y∈, 有W(ξ1-y)=W(ξ1).显然 下面给出本文的主要定理, 并应用两边夹定理、 Lyapunov泛函以及Lebesgue控制收敛定理进行证明. 定理1假设R0>1且Rd>1, 则对任意的c>c*, 系统(3)存在满足边界条件(4)的行波解(S(x+ct),I(x+ct)). 定义如下Lyapunov泛函: V(S,I)(ξ)=V1(ξ)+V21(ξ)+DII*V22(ξ), 其中 直接计算可得 由于(S*,I*)是系统(1)的平衡点, 因此有 (28) 将式(28)代入式(27)可得 此外, 有 根据文献[17]可知 (31) 且 联合式(29)~(32)可得 选取一族正的递增序列{ξk}k≥0, 满足当k→+∞时,ξk→+∞.定义 Sk(ξ)=S(ξ+ξk),Ik(ξ)=I(ξ+ξk). 假设Sk和Ik分别收敛到非负函数S∞和I∞.由于V(S,I)(ξ)是有界非增的, 所以存在一个常数C6和充分大的k, 满足 C6≤V(Sk,Ik)(ξ)=V(S,I)(ξ+ξk)≤V(S,I)(ξ), ∀ξ∈. 因此
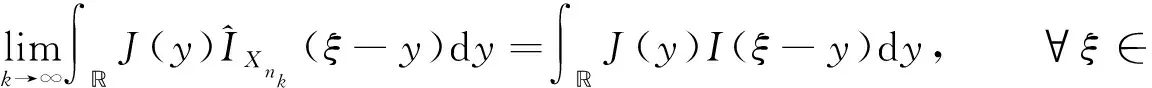

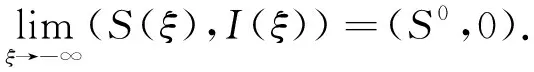
3 行波解的有界性
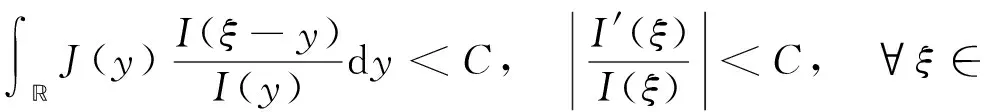

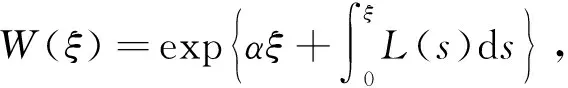


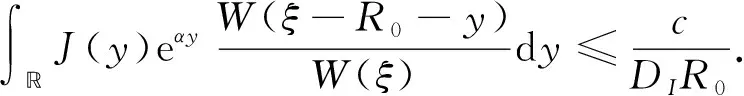
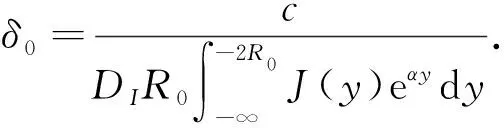
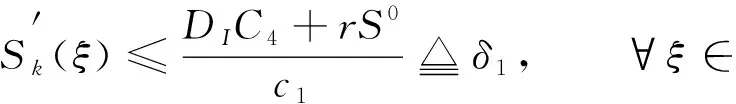
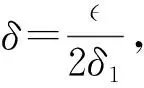
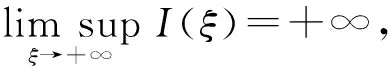
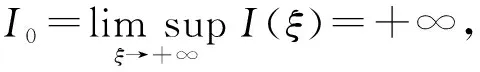
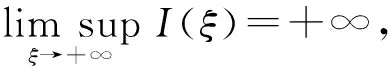
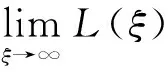
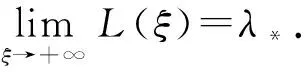
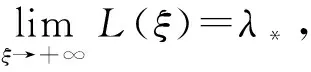
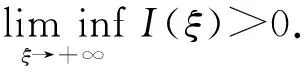
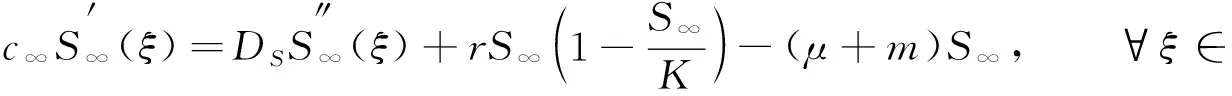


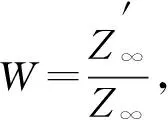
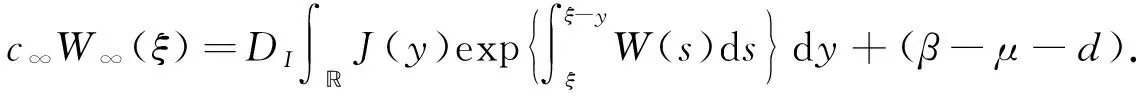
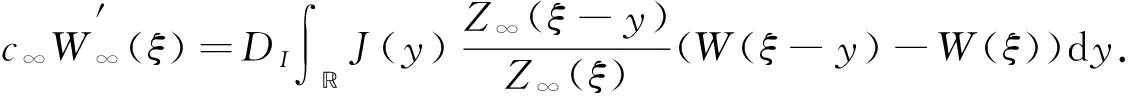
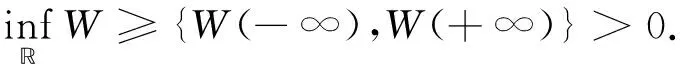
4 行波解的渐近行为