一类奇异分数阶微分方程边值问题正解的存在性
2022-07-07张彩玲
张 彩 玲
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
近年来, 由于分数阶微分方程在光学、 热学、 分数物理学、 黏弹性力学、 高分子材料的解链、 随机过程等领域的广泛应用而备受关注, 并取得了丰富的研究成果[1-10]. 文献[1]利用锥上混合单调算子的不动点定理, 考虑分数阶微分方程边值问题


受上述研究工作的启发, 本文利用Leggett-Williams不动点定理, 考虑奇异非线性分数阶微分方程边值问题

(1)

当p(t)=q(t)=1,Hu=0时, 文献[2]研究的问题即为问题(1)的特例.相比文献[1]研究的问题, 问题(1)中的非线性项多了导数项和算子项.
1 预备知识


则{E,‖·‖}为Banach空间.定义E上的锥
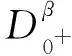

本文假设:
(H1)p,q: [0,1]→[0,+∞),K: [0,+∞)→[0,+∞)均为连续函数, 且
K(u(1))tα-1≤K(‖u‖);
(H2)f: [0,1]×(0,+∞)×[0,+∞)→[0,+∞)和g: [0,1]×(0,+∞)×(-∞,0)→[0,+∞)均连续, 存在e,v∈L1[0,1],R: [0,+∞)→[0,+∞)连续, 使得下列不等式成立:
0 定义1[11]函数y: (0,+∞)→的α(α>0)阶Riemann-Liouville分数阶积分定义为 定义2[11]函数y: (0,+∞)→的α(α>0)阶Riemann-Liouville分数阶导数定义为 定义3[11]设P是Banach空间E中的锥,ψ:P→[0,+∞)为连续函数, 若对∀x,y∈P及∀λ∈[0,1], 满足 ψ(λx+(1-λ)y)-λψ(x)-(1-λ)ψ(y)≥0(≤0), 则称ψ为P上的一个凹(凸)泛函, 记 Pr={x∈P|‖x‖ 1) 对任意的x∈P(α,a,b), {x∈P(α,a,b)|α(x)>a}≠Ø,α(Tx)>a; 2) 对任意的‖x‖ 3) 对任意的x∈P(α,a,c)且‖Tx‖>b,α(Tx)>a. 引理2[2]设h∈C[0,1], 则线性问题 (2) 有唯一解 (3) 其中 (4) 引理3[2]由式(4)定义的格林函数G(t,s)满足下列性质: 1)G: [0,1]×[0,1]→[0,+∞)是连续的; 2) 对任意的t,s∈[0,1], 有 3) 对任意的t,s∈[0,1], 有 (5) 其证明可见文献[2]中引理2.4. 因为式(1)中f,g为奇异函数, 因此要求出正解, 需先将f,g序列化和正则化.对任意的n∈, 记 (6) (7) 先考虑辅助问题: (8) 定义算子Tn:P→E为 由式(5)及定义2可知 引理4若条件(H1),(H2)成立, 则Tn:P→P为全连续算子. 证明: 令u∈P, 由条件(H1),(H2)及式(6),(7)得 0 设Ω⊂P是E中的有界集, 即u∈Ω时‖u‖≤L, 其中L为一个常数.由条件(H1),(H2)及式(9),(10)可知 故Tn(Ω)是E中的有界集. 为方便, 记 定理1令0 (i) 对所有的‖u‖∈(0,c], 有K(‖u‖) (ii) 对所有的t∈[δ,1-δ], ‖u‖∈[a,c], 有 其中δ∈(0,1/2); (iii) 对所有的‖u‖∈(0,d], 有K(‖u‖) 则辅助问题(8)至少存在3个正解u,u(1),u(2). 同理可得对所有的‖u‖∈(0,d], 满足条件(iii), 即引理1中条件2)成立. 即引理1中条件1)成立. 最后证明引理1中条件3)成立.由于Tn:P→P为全连续算子, 故存在常数δ∈(0,1/2), 使得u(t)≥δ‖u‖对∀t∈[δ,1-δ]成立.对∀u∈P(α,a,c), ‖Tu‖>b及δb>a, 有 根据引理1, 辅助问题(8)至少存在3个正解, 满足 下面考虑辅助问题(8)的解序列.由于问题(8)的3个正解u,u(1),u(2)满足的条件一致, 因此为方便以u为例进行讨论. 证明: 对所有的t∈[0,1],n∈, 有 根据式(13),(14)和条件(H1),(H2)可得 定理2设条件(H1),(H2)成立, 则边值问题(1)至少存在3个正解u,u(1),u(2). 因为{un}满足式(15), 故∃S>0, 使得‖un‖ 对∀t∈[0,1], 根据Lebesgue控制收敛定理, 得 当k→∞时, 根据 得 故u是问题(1)的正解, 同理可知u(1),u(2)也是问题(1)的正解.因此, 问题(1)至少存在3个正解u,u(1),u(2).



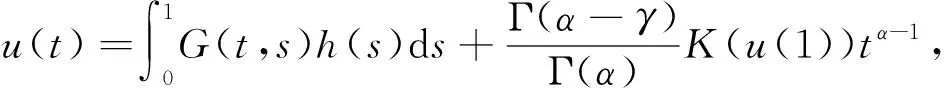








2 主要结果