基于IFLBP及空间隶属度相似性的CFFCM图像分割
2022-07-07王淑敏
兰 蓉,王淑敏
(西安邮电大学 通信与信息工程学院,陕西 西安 710121)
图像分割将图像分成互不重叠且各具特性的区域,是图像分析、识别和理解的基础。图像分割的种类繁多,基于聚类的图像分割方法一直是国内外研究的热点[1-3],而模糊C-均值[4](Fuzzy C-Means,FCM)聚类算法在图像分割中应用十分广泛。FCM算法的基本思想是通过建立目标函数,以模糊隶属度描述像素点与聚类中心之间的关系,通过循环迭代,使目标函数值达到最小,并以隶属度最大原则实现图像分割。
FCM算法具有简单、易于理解的优点,但其需要提前选择C个数据点作为初始聚类中心,在复杂数据集中,确定合适的聚类中心十分困难。基于此,Ding等[5]提出无中心模糊C-均值(Center-Free Fuzzy C-Means,CFFCM)聚类算法。该算法用样本点到类的相似度替换像素点到聚类中心的欧氏距离,适用于复杂数据集,但是其存在运行效率低,耗时长的问题。Bai等[6]对CFFCM算法进行改进并与可能性C-均值 (Possibilistic C-Means,PCM)聚类算法相结合,提高了算法抗噪性。随后,Bai等[7]又提出了直觉无中心模糊C-均值(Intuitionistic Center-Free Fuzzy C-Means,ICFFCM)聚类算法,将直觉模糊集引入到CFFCM中,并添加了局部信息项,对磁共振脑图像分割取得良好效果,但是计算复杂度较高。
CFFCM算法使用任意两点间距离计算像素点到类的相似性,因而导致算法复杂度过高。事实上,像素点对类别的归属与其局部及非局部空间像素点的关系密切,充分考虑像素点的局部或非局部空间信息,能够在一定程度上改善图像分割效果。如,肖满生等[8]提出了基于空间相关性及隶属度平滑的FCM算法(Fuzzy C-Means Based on Spatial Correlation and Membership Smoothing,SCMS_FCM)。该算法抗噪性较强,但涉及的参数较多,需要人工调整。Zhao等[9]在FCM算法中引入非局部空间信息,提出基于非局部空间信息的FCM (FCM with Non-Local Spatial information,FCM_NLS)算法,在保留图像细节信息的同时对噪声具有较强的鲁棒性。曹雪红等[10]提出基于非局部空间信息的截集式可能性 C-均值聚类(Cutset-type PCM_NLS,C-PCM_NLS)算法,构造非局部空间约束项,并引入到目标函数中,抗噪性较强,但其性能受截集门限的限制。兰蓉等[11]提出抑制式非局部空间直觉模糊C-均值(Suppressed Non-Local Spatial Intuitionistic Fuzzy C-Means,SNLS-IFCM)聚类图像分割算法,该算法能够为每个样本点对不同类别自适应地生成抑制因子,从而具有更好的鲁棒性。
针对CFFCM算法在图像分割过程中未考虑图像纹理信息以及依赖规模庞大的相似度矩阵,从而导致算法复杂度较高的问题,拟提出一种基于直觉模糊局部二值模式及空间隶属度相似性的 CFFCM (Center-Free Fuzzy C-Means Based on Intuitionistic Fuzzy Local Binary Pattern and Spatial Membership Similarity,CFFCM_IFLBPSMS)图像分割算法,对CFFCM算法在运行效率及分割效果方面进行改进。利用像素的局部及非局部空间信息,结合邻域隶属度设计一种新的衡量像素点到类的相似性的计算方法,以期提高CFFCM算法的运行效率,改善分割结果。同时,利用直觉模糊局部二值模式[12](Intuitionistic Fuzzy Local Binary Pattern,IFLBP)定义直觉模糊局部二值模式纹理特征,有效刻画图像细节中的不确定性信息,并将其引入目标函数,在一定程度上抑制光照不均匀对分割效果的影响。
1 相关研究
1.1 CFFCM算法
Ding等[5]认为在复杂数据集中可能并不存在聚类中心,因此在CFFCM算法中用样本点到类的相似度替换像素点到聚类中心的欧氏距离。设样本集X={x1,x2,…,xn},n为样本点总个数,将其划分为c类,则CFFCM算法的目标函数为
(1)
式中:m为模糊化参数(一般设为2);uki和ρki分别为第i个样本点对第k类的隶属度和相似性,ρki的计算表达式为
(2)
式中,ωei是任意两点之间的相似性,定义为
(3)
式中,dei=‖xe-xi‖为任意两点之间的欧氏距离,β为经验参数。
利用拉格朗日乘子法,可得隶属度的迭代表达式为
(4)
由此可知,CFFCM算法的聚类过程与聚类中心无关。
1.2 直觉模糊局部二值模式
将直觉模糊集引入图像纹理的局部模式表示中,可得IFLBP[12],其是模糊局部二值模式[13](Fuzzy Local Binary Pattern,FLBP)的推广。
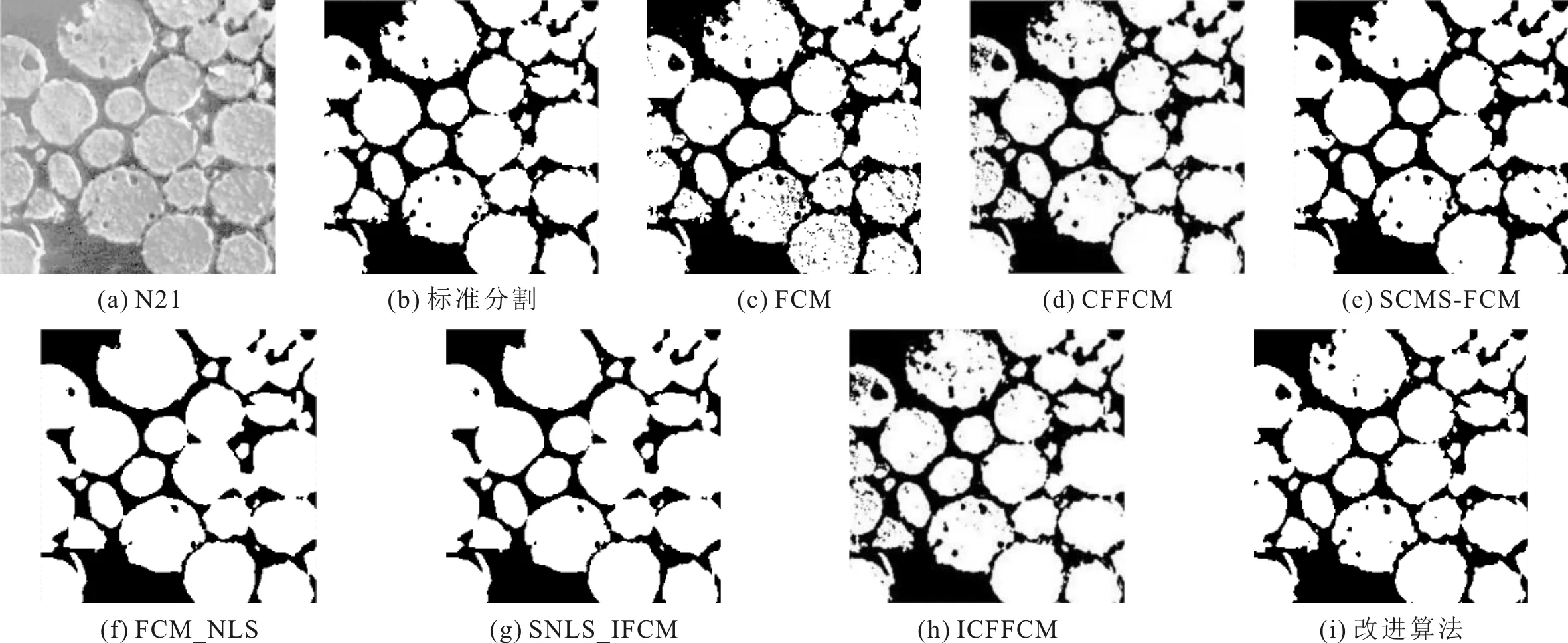
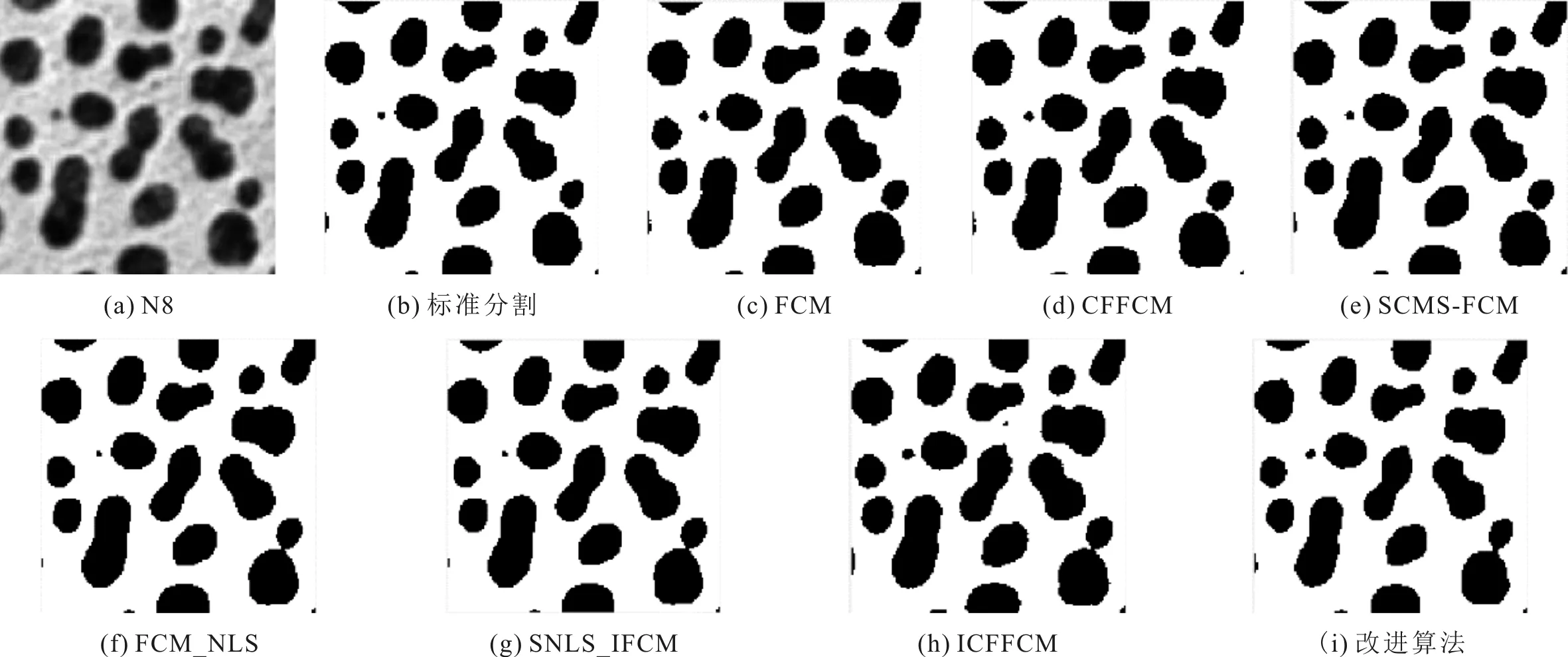
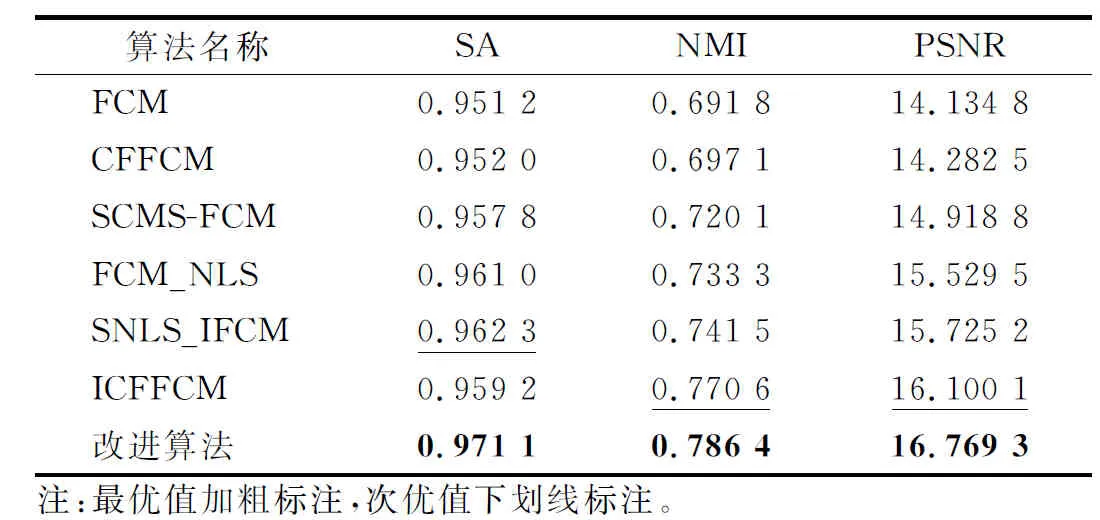
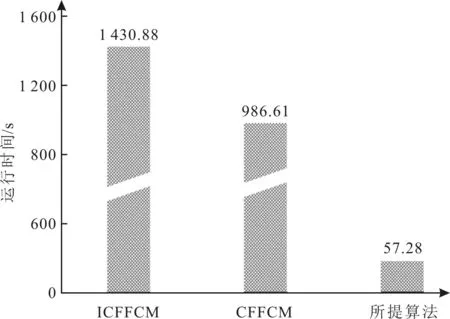
假设图像包含n个像素点,令像素邻域集为U={0,1,…,z-1},A为U中灰度值xj≥xi的所有像素的集合,B为U中灰度值xj A={[xj,μA(j),vA(j)]|xj∈U} (5) 式中,μA和vA分别表示元素的隶属度函数和非隶属度函数。μA:U→[0,1],vA:U→[0,1],且满足0≤μA(j)+vA(j)≤1,∀xj∈U。 直觉模糊集A的隶属度和非隶属度分别定义为 (6) (7) 式中:T为模糊程度控制参数,控制模糊范围;η为犹豫阈值。 对于z个邻域像素,每个模式的贡献度值由隶属度和非隶属度计算可得,定义为 (8) 其中, (9) 在每个像素邻域集U中,所有模式贡献度之和为1,即 (10) 式中:b为邻域中处于模糊状态的像素个数;2b为各像素点模式总数。 对任意中心像素xi,其局部邻域的第t个模式的唯一IFLBP编码表示为 (11) 若在局部邻域内存在b个像素的强度值介于[xi-T,xi+T]之间,则可分为2b个模式,并得到2b个IFLBP码。因此,对于3×3局部邻域至多存在256个模式。 易知,当T≠0,η=0时,IFLBP退化为FLBP;T=0,η=0时,IFLBP退化为LBP。 CFFCM算法在处理图像过程中存在计算缓慢的缺点,运行效率较低且对纹理复杂图像分割效果不佳。考虑到像素点对各类别的归属与像素点局部及非局部空间中的像素点关系密切,将设计一种新的衡量像素点到类相似性的计算方法。利用局部及非局部窗口像素灰度值计算邻域相对重要性,结合邻域隶属度获得像素点到类的相似性,节省计算耗时,并在此基础上定义IFLBP纹理特征,将图像的纹理信息引入到CFFCM算法的目标函数中,进一步提升图像分割的效果。 CFFCM算法在计算样本点到类的距离时依赖于一个庞大的相似度矩阵,该矩阵的规模与样本点数目有关,使得在分割较大图像时,算法的复杂度增加。为改善算法的运行效率,引入像素的空间信息,设计一种新的衡量像素点到类相似性的方法,即,结合空间信息的隶属度相似性。 对于待分类像素而言,其类别不仅与其自身特征有关,而且与其局部及非局部邻域像素具有较大的相关性,因此结合空间信息的隶属度相似性可表示为 (12) 式中:uki和ukj分别为像素xi及其局部邻域像素xj对第k类的隶属度;li和wi分别控制局部窗口及非局部窗口中邻域的相对重要性,定义为 (13) (14) (15) 经分析可知,h的取值与图像的受噪声影响程度成正比,当图像中的噪点较多时,h值较大,反之亦然。通过计算图像中所有像素点的邻域标准差衡量图像的受噪声影响程度,并利用所有像素点对h参数进行全局自适应选取,其计算表达式为 (16) 该部分有两点说明:1)与像素xi具有相似局部邻域结构的像素具有较小的li值;2)与像素xi具有相似非局部邻域结构的像素具有较大的wi值。 对原图像应用IFLBP算法得到纹理特征,定义可视化纹理集X′={x′1,x′2,…,x′n},对于任意的x′i∈X′,i∈{1,2,…,n},计算表达式为 (17) 对于具有丰富纹理信息的图像来说,其分割目标内部的像素点与邻域像素点相差较大,采用标准方差函数对可视化纹理集X′中所有元素的局部邻域进行处理,可以扩大目标与背景的差异。x′i局部邻域的标准差表示为 (18) 为了与像素灰度值的取值范围保持一致,将σ′i标准化到[0,255],定义为 (19) 控制参数T对可视化纹理集具有很大的影响,不恰当的选值会导致目标和背景的差异减小,从而造成误分类。为了尽量避免类别错分现象,采用均值滤波对Mσ′i进行处理,得到最终的IFLBP纹理特征,即 (20) 式中,a为滤波窗口大小,此处取3。 结合空间信息的隶属度相似性,采用IFLBP 算子提取图像的纹理特征,对 CFFCM 算法进行改进,得到 CFFCM_IFLBPSMS 图像分割算法,其目标函数表示为 (21) 式中:Ski和S′ki分别为图像像素点xi和IFLBP纹理特征x′i对第k类的相似度;参数λ控制IFLBP纹理特征的作用。 利用拉格朗日乘子法得到新的隶属度函数的计算表达式为 (22) CFFCM_IFLBPSMS图像分割算法具体实现步骤如下。 步骤1初始化参数。设置聚类数目c,模糊化参数m=2,最大迭代次数M=100,迭代终止阈值ε=10-6,迭代次数初始值y=0,局部邻域大小z=8,搜索窗大小f×f,相似窗大小s×s,控制参数λ,IFLBP纹理特征中的T和η。 步骤2提取纹理特征。利用式(17)—式(20)得到最终的IFLBP纹理特征FIFLBP。 步骤3利用传统FCM算法对原始图像及IFLBP纹理特征分别初始化隶属度矩阵。 步骤4利用式(13)和式(14)计算局部及非局部空间信息li、l′i和wi、w′i。 步骤5利用式(12)计算点到类的相似度Ski和S′ki。 步骤6利用式(22)计算隶属度函数uki并且y=y+1。 步骤7若‖U(y+1)-U(y)‖<ε或者y>M,则算法结束;否则,返回步骤5。 CFFCM_IFLBPSMS算法的时间复杂度按照复杂度分析方法[9]可分为3个部分:1)IFLBP纹理特征提取的时间复杂度为O1(nz+n2b+na2),这部分属于图像的预处理过程,可以提前计算;2)空间隶属度相似性计算的时间复杂度为O2(ns2f2+nz);3)算法迭代分割过程的时间复杂度为O3(ncy)。因此,该算法的最终时间复杂度为以上3部分之和,即O(nz+n2b+na2+ns2f2+nz+ncy)。 CFFCM算法的时间复杂度分为两个部分:第一部分为相似度矩阵计算,其时间复杂度为O(n2);第二部分为算法迭代分割过程,其时间复杂度为O(ncy)。因此,算法的时间复杂度为O(n2+ncy)。 一般的,图像大小,即像素数n远大于像素邻域操作中的相关半径参数a、s、f和z。因此,CFFCM_IFLBPSMS算法的时间复杂度远低于CFFCM算法,尤其是当图像较大时,这种差别会更加显著。由此可知,结合空间信息的隶属度相似性可提高算法的运行效率。 为了验证改进算法的有效性,选取Berkeley图库数据集[14]和文献[15]图库,分别与FCM、CFFCM[5]、SCMS-FCM[8]、FCM_NLS[9]、SNLS_IFCM[11]和ICFFCM[7]等6种算法进行性能对比实验。实验环境为Windows 10,Inter(R) Core(TM)i7-6567U,4.00G RAM,采用 Matlab R2019a 进行仿真。性能评价指标为分割准确率[16](Segmentation Accuracy,SA)、归一化互信息[17](Normalized Mutual Information,NMI)和峰值信噪比[18](Peak Signal to Noise Ratio,PSNR)。上述3个指标均为效益型指标,其值越大表明算法的分割性能越好。 在Berkeley图像数据集中选取#147091、#253036和#100007等3幅图像。参数设置为c=2、f=10、s=3、λ=0.5、T=10和η=0.5。 将3幅图像转化为灰度图,如图1(a)、图2(a)和图3(a)所示。图像#147091的分割难点在于曝光不当引起的天空四角光照不均匀且树的枝叶纹理较为复杂。图像#253036的天空右上角存在光照不均匀的情况且分割目标内部存在一些小的孔洞。图像#100007山上的雪与冰面灰度相似且面积较大,难以区分。7种算法图像分割可视化结果分别如图1至图3所示。 图1 7种算法对图像#147091的分割结果 图2 7种算法对图像#253036的分割结果 图3 7种算法对图像#100007的分割结果 参考图1至图3中(b)图即标准分割可知,受光照不均匀的影响,FCM和CFFCM算法无法准确分割出目标部分。由于融合了局部或非局部的空间信息,SCMS-FCM、FCM_NLS和SNLS_IFCM算法在处理细小孔洞或者噪声干扰方面具有一定的优势,但对天空及山体部分的分割效果不佳。ICFFCM算法解决了图像光照不均匀的问题,但对于纹理较为复杂的部分及细小的空洞存在误判。改进算法利用IFLBP提取图像的直觉模糊纹理信息,能够较为完整的分割图像#147091及#253036的树枝部分。对于光照不均匀引起的图像边角难以分割以及图像#100007山上雪不连续且大片出现的问题,改进算法中邻域隶属度及空间信息的引入可能是解决以上问题的原因。因此,改进算法对以上3幅图像的分割结果较好。 表1为7种算法的评价指标对比,可以看出,改进算法的各项指标均为最优或仅次于ICFFCM算法,说明改进算法能够有效提高图像分割的准确率。 表1 7种算法对3幅图像的评价指标对比 在文献[15]图库中选取N42、N21和N8等3幅图像。参数设置为c=2、f=10、s=3、λ=0.25、T=10和η=0.5。 3幅图像中N42存在灰度分布不均匀的现象,N21内部存在较多噪点且包含较多细节,N8目标边缘较为模糊,7种算法对3幅图像的分割结果分别如图4至图6所示。 图4 7种算法对图像N42的分割结果 图5 7种算法对图像N21的分割结果 图6 7种算法对图像N8的分割结果 由图4至图6可知:改进算法对图像N42左上部分的错分最小;去除图像N21噪声的同时能够保留细节,与标准分割最为相近;对于图像N8边界不清晰,难以精确分割的问题,改进算法对图像目标边界像素点邻域像素灰度值及隶属度的引入,对图像分割的准确率产生积极影响,使得难以分割的模糊边界得到较好的结果。 7种算法对文献[15]图库中的3幅图像评价指标对比如表2所示。可以看出,改进算法在各项指标中具有一定优势,尤其是图像N8,逼近于标准分割。 表2 7种算法对3幅图片的评价指标对比 为了客观分析算法性能,获得相对可靠的实验结论,在Berkeley图库中选取了#15088、#3096、#41004、#24063、#147091、#14037、#227046、#28083、#117025、#253036、#101027、#167062、#100007、#62096、#241004等15幅图像,用7种算法对15幅图像分别进行分割实验,并统计SA、NMI和PSNR等3种评价指标的平均值,如表3所示。 表3 7种算法相应评价指标平均值对比 由表3的统计结果可知,改进算法在15幅图像的分割实验中,各项指标平均值都是最优的。由于结合了空间信息,SCMS-FCM、FCM_NLS以及SNLS_IFCM算法对于噪声较多的图像以及目标主体内部存在细小干扰的图像,处理结果较好,各项指标值高于传统FCM及CFFCM算法。ICFFCM算法将直觉模糊集概念引入到了CFFCM算法中,能够对不精确、不确定性信息得到更好的处理结果,并且引入了空间信息项,对噪点较为鲁棒。因此,对大多数图像的分割结果较好,但对个别图像,如#3096的分割结果不佳,性能不稳定,导致ICFFCM算法的性能指标次于改进算法。而改进算法在15幅图像的分割实验中结果比较稳定,表现出较好的性能。 改进算法对CFFCM算法运算时间长的问题进行了改进,而ICFFCM算法是CFFCM算法的另一种改进算法。因此,分别选取CFFCM、ICFFCM算法与改进算法进行运行效率对比。 为客观评价CFFCM算法、ICFFCM算法以及改进算法的运行效率,分别在文献[15]图库选取图像大小为240×240、Berkeley图库中图像大小为481×321的15幅图像进行测试,3种算法的平均运行时间分别如图7和图8所示。为便于观察对比,采用截断坐标轴方式进行绘图。 图7 3种算法在文献[15]图库上分割图像的平均速度 图8 3种算法在Berkeley图库上分割图像的平均速度 由图7和图8可知,改进算法的运行时间明显少于CFFCM算法和ICFFCM算法,相较于这两种算法,改进算法快了近一个数量级,这与算法时间复杂度分析得到的结论是一致的。 事实上,计算像素点间相似性时,CFFCM算法采用枚举方式,逐点计算是造成其运行速度缓慢的重要因素。设计的结合局部及非局部空间信息的隶属度相似性计算公式,在衡量像素点到类的相似性时仅使用到了像素点局部及非局部邻域在灰度值及隶属度方面对其的影响,而非整幅图像的像素,从而能够缩短算法的运行时间。ICFFCM算法在计算像素点间相似性时,考虑了像素点间灰度关系及坐标关系,并且在目标函数中引入了空间信息项,使得算法复杂度较高,虽然在实验中分割准确率较高,但运行效率甚至低于CFFCM算法。 结合IFLBP及空间隶属度相似性改进的CFFCM算法采用空间隶属度相似性改善了原始像素点到类的相似度,利用像素点的局部及非局部空间像素灰度值以及邻域隶属度,提升了算法运行效率。同时,利用IFLBP算子定义图像IFLBP纹理特征,从而提高了算法处理纹理复杂图像的能力,提升了算法对图像的分割精度。仿真实验结果表明,改进算法相比其他6种算法,在处理纹理复杂、光照不均匀和边界不清晰的图像中均具有较好的分割结果。相较于CFFCM算法,改进算法在运行效率提高了近一个数量级。2 改进的CFFCM算法
2.1 结合空间信息的隶属度相似性
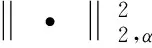
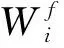

2.2 IFLBP纹理特征提取

2.3 CFFCM_IFLBPSMS图像分割算法
2.4 时间复杂度法分析
3 实验结果及分析
3.1 Berkeley图库图像分割实验

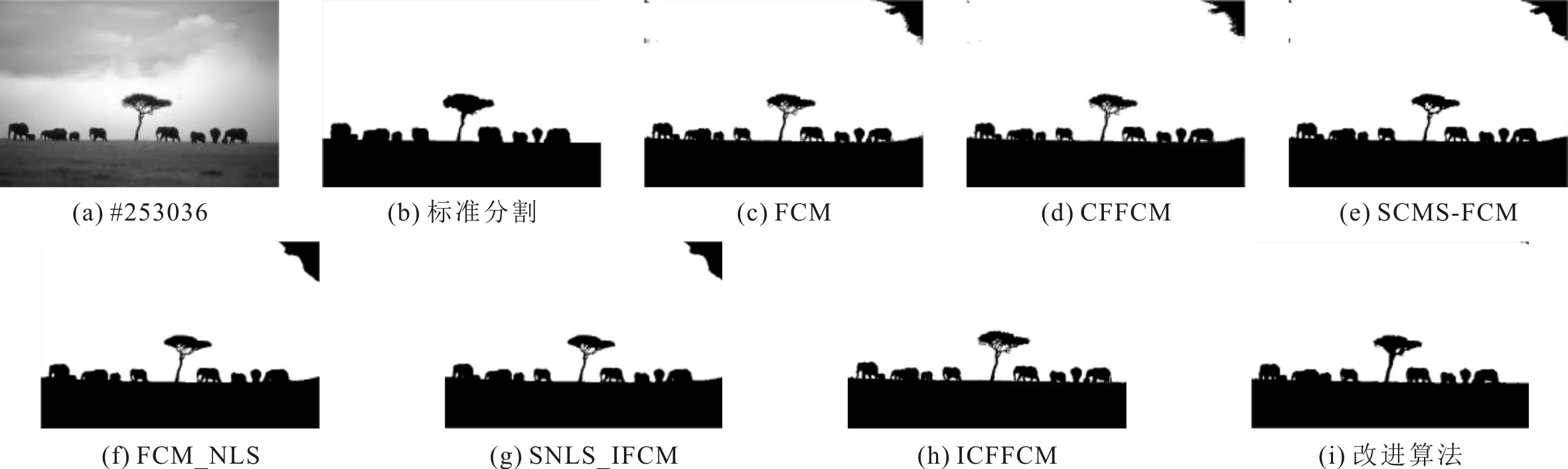

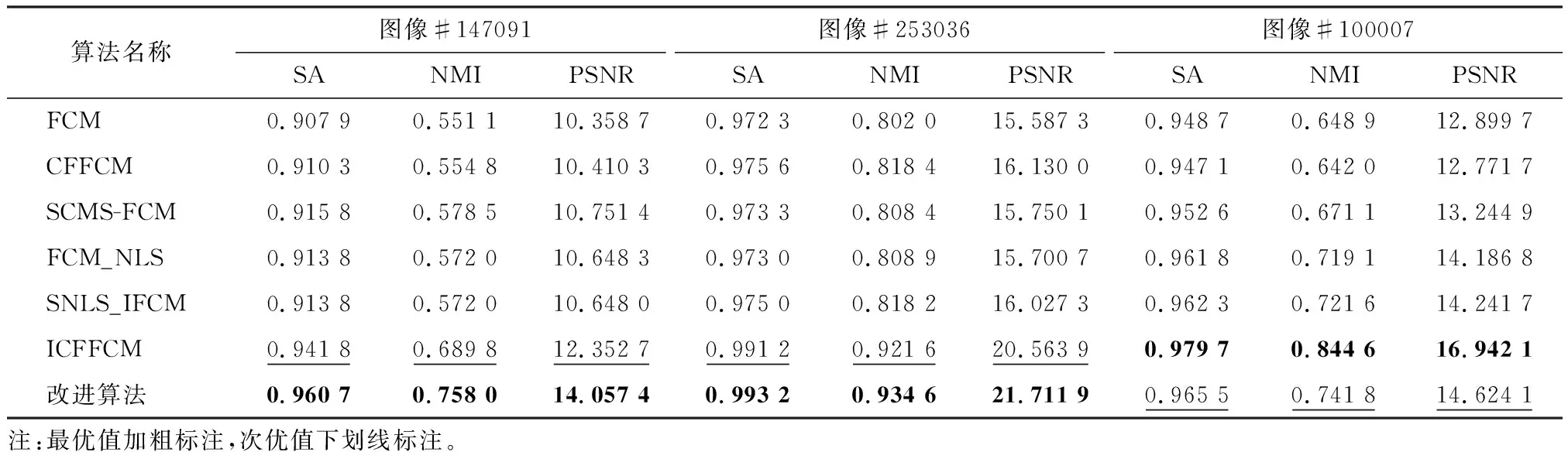
3.2 文献[15]图库图像分割实验


3.3 算法性能指标总体分析
3.4 算法运行效率分析

4 结语
