基于概率语言和区间数的多属性决策TOPSIS 方法及其应用

彭 怡

(西南民族大学数学学院，四川成都 610041)

多属性决策问题是一类复杂优化决策问题，在工程领域、经济领域、军事领域、公共管理领域经常出现.在多属性决策过程中，决策属性值经常具有信息不确定、数据难以估计预测、评价意见模糊等情形，这比决策属性值为精确数据和明确信息更具有普遍性.决策问题具有多个决策属性，对于定性决策属性，决策属性值通常以语言评价形式呈现，如优秀、良好、合格、不合格等语义信息，这为数学计算和分析带来困难，简单地对语义信息进行数量转换，比如设定等级评分，无法保证科学性，容易丢失重要信息，导致决策失误.对于语言信息的决策处理是目前的研究热点，其中概率语言是一类研究和应用较多的语言信息类别，可用于解决多属性决策过程中的语言信息处理问题.此外，当决策属性值无法获取精确数据时，在某个估计值附近做出一个变动范围估计，对于决策者更容易实现，决策属性值也更有利用价值. 对候选方案的决策属性值预测一个取值区间，而不是确定一个精确值，此时决策属性值就是一个区间数.因此，本文研究决策属性值同时表现为概率语言和区间数情形下的具有混合形式模糊决策属性值的多属性决策问题.

文献[1]在犹豫模糊语言基础上定义了概率语言术语集，对概率语言多属性决策问题进行研究. 文献[2]将PROMTHEE II 与概率语言结合应用于决策.文献[3]研究了概率语言熵用于多属性决策. 文献[4]研究基于概率语言术语集的VIKOR 多属性决策方法.文献[5]将概率语言信息与前景理论结合进行研究.文献[6]提出了概率语言术语集加权类Pearson综合相关系数，文献[7]引入了互动与反馈过程，文献[8]提出了双投影法.而关于区间数的研究，文献[9]对区间数排序方法进行了总结，文献[10]对区间数的距离测度进行了改进研究，文献[11]研究了带分布区间数的排序问题，文献[12]将区间数与TOPSIS 结合应用，文献[13]研究了属性权重未知的区间数多属性决策问题，文献[14][15]研究了区间数熵与TOPSIS方法结合应用.

基于上述文献中关于概率语言和区间数的相关理论，本文研究同时具有区间数属性值和概率语言属性值的多属性决策问题.

1 概率语言信息评价

概率语言信息属于定性评价，通过语义形式对候选方案进行评价，具有模糊性、广泛性、实用性，在多属性决策过程中是一个处理难点.下面给出本文相关的概率语言术语集理论.

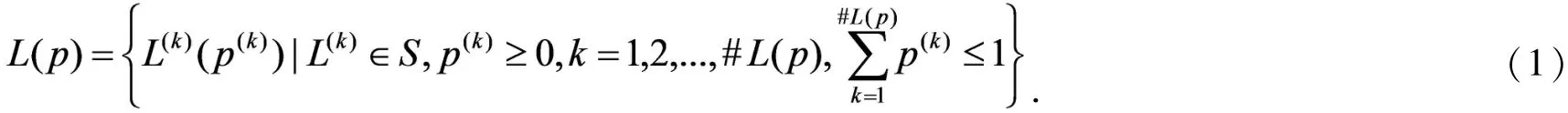
其中

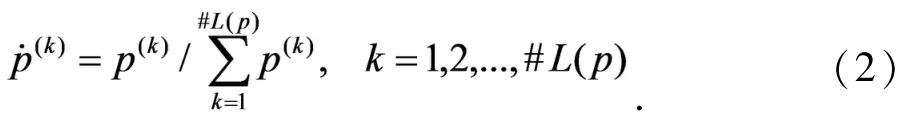
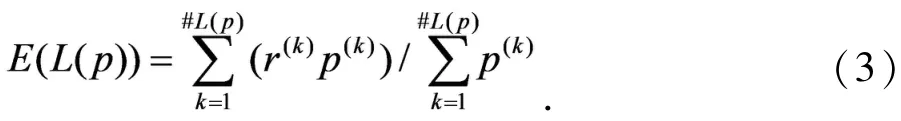
偏离度函数为

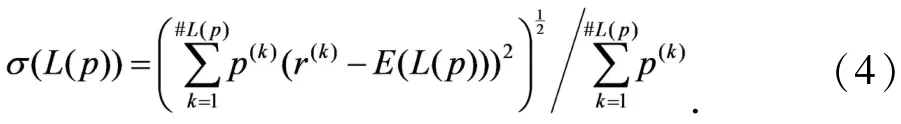
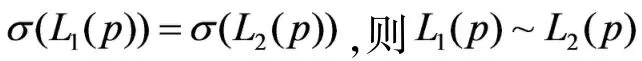
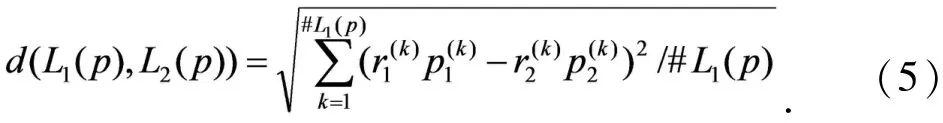
2 区间数信息处理

在多属性决策过程中，经常需要对候选方案的属性值进行定量预测，而给出精确预测值往往是困难的，采用区间数进行模糊定量评价是比较可行的处理方法.下面给出本文相关的区间数的基本理论.

定义5:

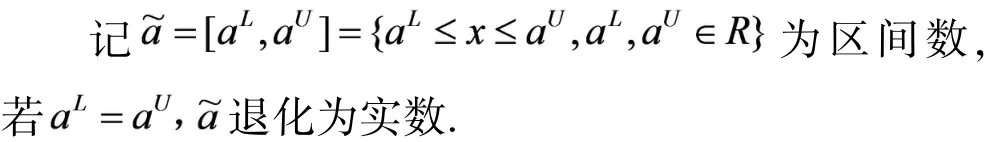
区间数的运算法则，定义如下:

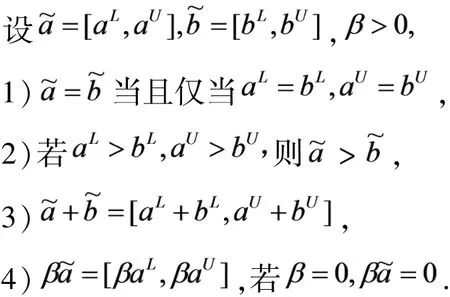
hamming 距离:

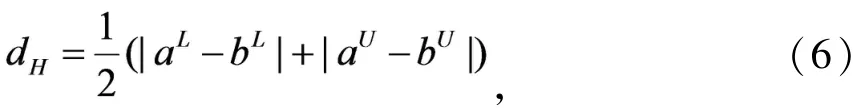
Euclidean 距离:

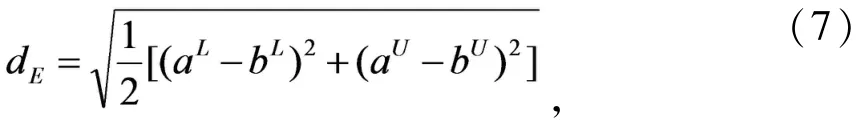
中心距离:

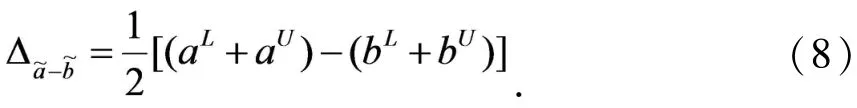
3 属性值为区间数和概率语言集的改进 TOPSIS 方法

表1 多属性评价结果Table 1 Results of Mmulti-attribute Evaluation

对区间数属性值做规范化处理:

对效益型属性，令

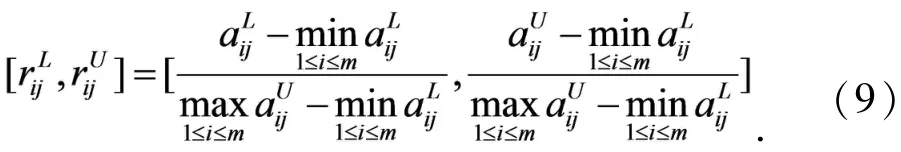
对成本型属性，令

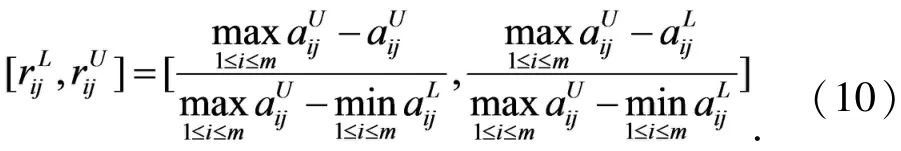
通过上述规范化处理，可将区间数属性值规范到[0，1]区间并消除量纲差异，优于其他方法. 应用TOPSIS 方法决策需要确定正理想点和负理想点.

对规范化区间数属性:

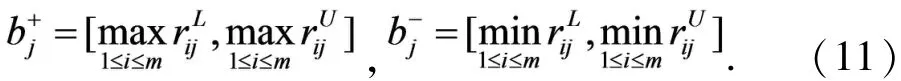
对效益型概率语言术语集属性:

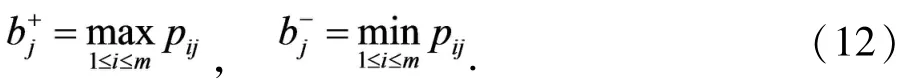
对成本型概率语言术语集属性:

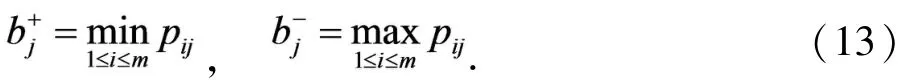
概率语言术语集大小按照前述定义3 进行大小比较.

进一步计算各方案与正理想点的距离和与负理想点的距离，区间数属性按照公式(8)计算，概率语言术语集属性按照公式(5)计算，考虑各属性权重计算各方案与正负理想点的加权距离di＋，di-，再计算与正理想点的贴近度

根据各方案贴近度大小可排序选优.

4 算例分析

表2 多属性评价结果Table 2 Results of Mmulti-attribute Evaluation

按照前述公式(9)对区间数属性值做规范化处理，再按照公式(11)(12)计算得到正理想点Z＋={[0.5，1]，[0.6，1]，{s5(0.3)，s6(0.7)}，{s5(0.4)，s6(0.6)}，{s5(0.7)，s6(0.3)}}和负理想点Z-={[0，0.4]，[0，0.2]，{s3(0.4)，s4(0.6)}，{s3(0.2)，s4(0.8)}，{s2(0.2)，s3(0.8)}}，按照公式(5)(8)并考虑属性权重计算与正负理想点的加权距离di＋，di-如表3 和表4.

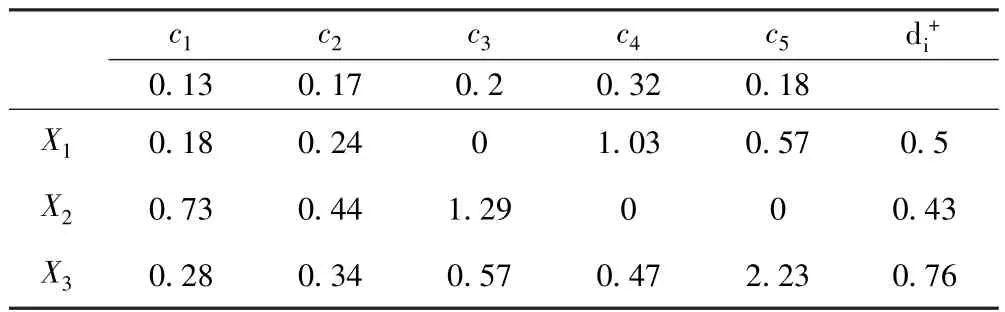
表3 各方案与正理想点距离Table 3 Distance of each scheme and positive ideal solution

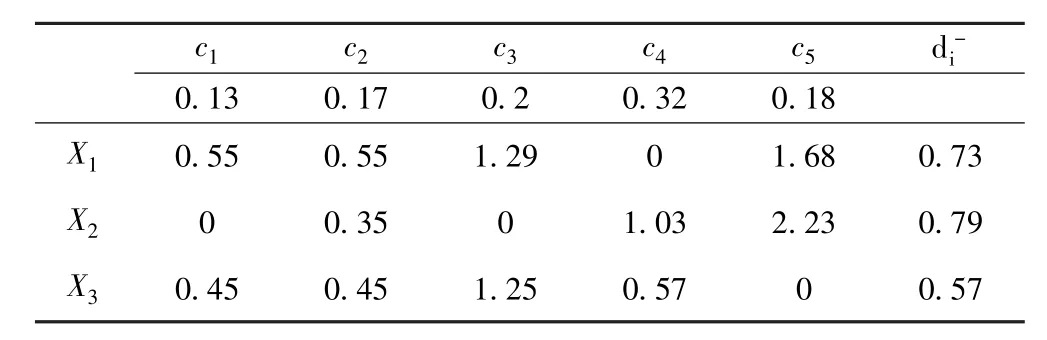
表4 各方案与负理想点距离Table 4 Distance of each scheme and negative ideal solution

由公式(14)得到方案X1，X2，X3的贴近度依次为(0.59，0.65，0.43)，于是方案排序为X3■X1■X2.

5 结论

本文所研究的同时具有区间数属性值和概率语言属性值的多属性决策问题，更符合实际决策情形，使得多属性决策过程更容易完成.相应产生的混合形式模糊决策属性值，本文给出了决策属性值的综合处理过程，提出了改进TOPSIS 方法，使得决策过程和决策结果科学严谨.对于区间数和概率语言术语集还有其他处理方法，本文采用的计算方法较为简便.