膜盒式贮箱金属膜盒疲劳寿命预测与试验
2022-07-07乔艳伟王婷婷赵和明鲁思源
范 凯,乔艳伟,王婷婷,赵和明,鲁思源
(1.上海空间推进研究所,上海 201112; 2.上海空间发动机工程技术研究中心,上海 201112)
0 引言
膜盒式贮箱作为一种可实现推进剂重复加注和排放的推进剂贮箱,可应用于在轨航天器的推进剂补加和金属膜片贮箱的温度交变补偿。目前国际空间站所采用的推进剂补加技术就是通过膜盒式贮箱实现的,也是目前应用最为广泛和成熟的补加技术。
膜盒式贮箱一般由圆柱形贮箱壳体和类似波纹管结构的金属膜盒组成,具体结构如图1所示。其由膜盒将贮箱腔体隔离形成液腔和气腔,并通过膜盒的拉伸和压缩来实现液体推进剂的加注和排出功能,类似结构同样应用于液体火箭蓄压器和液体火箭发动机涡轮泵端面密封结构上。膜盒结构复杂,在其制造加工过程中不可避免会出现各种缺陷和变形。同时,其工作过程中由于重复拉伸和压缩而承受周期性变化的载荷。在交变载荷的反复作用下,膜盒会在应力集中位置或缺陷处逐渐累积疲劳损伤,当损伤累积达到一定程度时,膜盒发生疲劳失效,进而造成推进系统工作异常甚至导致任务失败。因此,准确预测金属膜盒的疲劳寿命具有重要的实际意义。
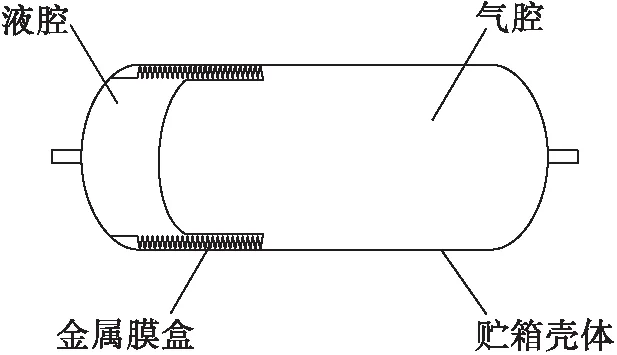
图1 金属膜盒推进剂贮箱Fig.1 Metal bellows propellant tank
针对金属材料疲劳失效及预测问题国内外学者已经开展了大量研究。文献[7-8]使用剩余强度模型研究金属疲劳失效问题,实验表明,金属结构的疲劳寿命受应力幅值和应力均值的影响显著。经典的疲劳寿命模型只根据应力幅值进行寿命预测,这会导致预测结果与实际情况偏差较大。针对上述两者综合影响,阎楚良等基于三参数S—N曲线方程和等寿命图模型,建立了描述应力幅值、应力均值和疲劳寿命三者关系的疲劳性能广义S—N曲面方程。张书明等考虑应力幅值和应力均值的综合影响,基于Forman和Walker裂纹扩展模型,建立了描述材料疲劳断裂性能的广义S—N曲面方程。熊峻江等对传统的等寿命曲线方程进行推广和扩展,给出了广义疲劳等寿命曲线的统一表达式,并研究了二维疲劳极限的概率分布特性。
由于金属膜盒在实际工程应用中所承受载荷的复杂性和多样性,如果对每种载荷工况下的疲劳寿命均采用试验的方法来确定,时间和经济成本巨大,在工程实践中很难实现。为有效解决问题,本文基于恒幅循环载荷下的基本疲劳试验数据,通过一定的模型修正及疲劳损伤理论分析,对不同载荷工况下的疲劳寿命进行预测,并通过试验验证了该方法的准确性。
1 修正的广义应力-疲劳寿命曲面
在工程中,应力-疲劳寿命曲线(S—N曲线)是表征材料疲劳性能的基本曲线,其描述的是最大循环应力和疲劳寿命之间的对应关系,即

(1)
式中和为材料参数。
工程中通常采用等寿命模型描述材料给定疲劳寿命时应力幅值和应力均值之间的变化关系。最常用的等寿命模型包括Goodman模型、Gerber模型和Soderberg模型,其表达式如下。
Goodman模型表达式为
=(1-)
(2)
Gerber模型表达式为
=[1-()]
(3)
Soderberg模型表达式为
=(1-)
(4)
式中:为对称疲劳极限;为抗拉强度;为屈服强度。
若已知应力幅值和应力比(=/),则最大应力=2/(1-),应力均值=[(1+)/(1-)],再联合式(2)、式(3)和式(4)可得到修正后的广义应力—疲劳寿命曲面(--曲线)。
基于Goodman模型修正的表达式为
{2[(1+)+(1-)(-)]}=
(5)
基于Gerber模型修正的表达式为

(6)
基于Soderberg模型修正的表达式为
{2[(1+)+(1-)(-)]}=
(7)
2 修正的Miner累计损伤准则
当循环应力作用一次时,疲劳损伤量(1)为
(1)=1/(,)
(8)
式中(,)为循环应力(,)作用下的疲劳寿命,由式(5)、式(6)、式(7)确定。
当循环应力作用次时,疲劳损伤量为

(9)
式中(a,m)为循环应力(a,m)作用下的疲劳寿命,同样由式(5)、式(6)、式(7)确定。
当循环应力作用次数达到材料疲劳寿命时,材料发生疲劳破坏。在工程应用中,认为此时的临界损伤量为1。
3 金属膜盒全行程循环工作疲劳寿命预测
3.1 膜盒材料及其广义Sa —Sm—N曲面
目前膜盒式贮箱膜盒材料通常为不锈钢SUS304,材料性能参数见表1。

表1 室温下SUS304材料性能Tab.1 Mechanical properties of SUS304 at room temperature
文献[21]中按照ASTME606—92标准对304不锈钢进行了不同应力水平下的疲劳试验,数据见表2。

表2 室温下304不锈钢不同循环应力下的疲劳次数Tab.2 Fatigue number of 304 stainless steel under different cyclic stresses at room temperature
对上述数据采用幂函数拟合得到曲线参数=8.66,=1.3×10。将和分别代入式(5)、式(6)、式(7)即得到基于Goodman模型、Gerber模型和Soderberg模型修正的304不锈钢广义——曲面。曲面方程如式(10)~式(12)所示,并绘制了相应的曲面图形,见图2。

图2 修正的304不锈钢广义Sa—Sm—N曲面Fig.2 Modified generalized Sa—Sm—N curved surfaces of 304 stainless steel
{1 556/[(1+)+(1-)(778-)]}=
1.3×10
(10)
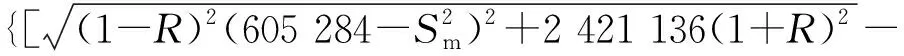

1.3×10
(11)
{592/[(1+)+(1-)(296-)]}=
1.3×10
(12)
3.2 膜盒尺寸和全行程
金属膜盒为环柱形结构,具体结构和几何尺寸如图3所示。其中膜盒外波峰直径=170 mm,内波谷直径=150 mm,外波峰和内波谷之间由两组直线段和两组圆弧段连接。连续两个外波峰为一组,该膜盒共5组。
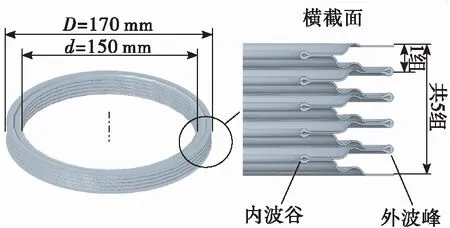
图3 金属膜盒结构及几何尺寸Fig.3 Structure and geometry dimension of metal bellows
金属膜盒未工作时的初始高度为=18 mm。当其处于推进剂排放工作状态时,膜盒逐渐被压缩,最大压缩行程位置对应的膜盒高度为=7 mm;当其处于推进剂加注工作状态时,膜盒逐渐被拉伸,最大拉伸行程位置对应的膜盒高度为=35 mm。上述3个典型膜盒行程位置如图4所示。膜盒从最大压缩行程位置到最大拉伸行程位置再到最大压缩行程位置(→→)即为完成一次全行程。
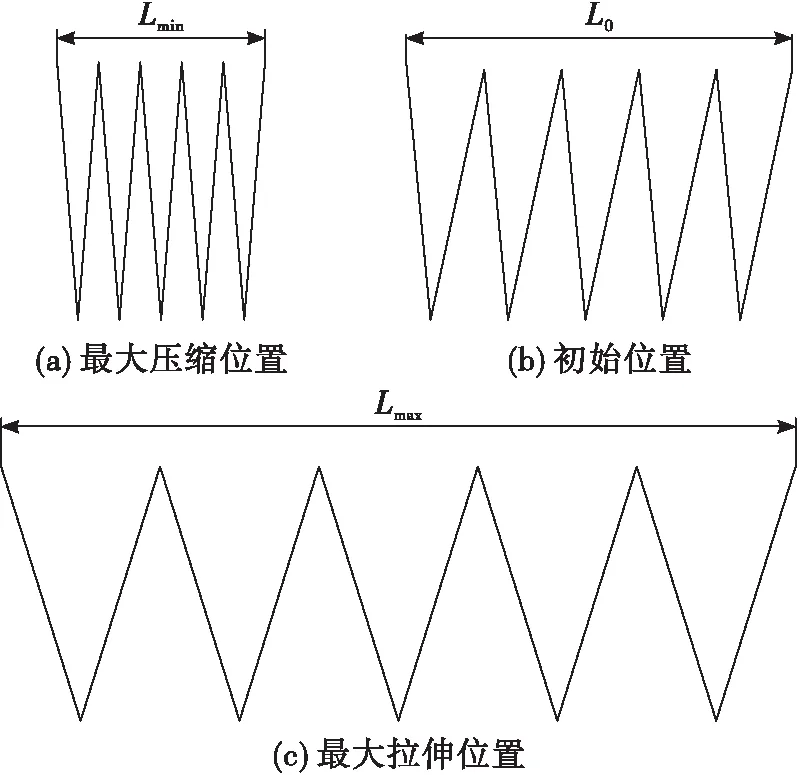
图4 金属膜盒典型行程位置Fig.4 Typical stroke position of metal bellows
3.3 Sa、Sm和R的计算
为了得到金属膜盒在全行程工作(→→)状态下的循环应力参数(、和),采用ABAQUS/Standard有限元软件对上述膜盒进行静态加载模拟。考虑到膜盒结构是轴对称的,故选用轴对称平面模型,如图5所示。这里需要注意的是,由于该膜盒直径与其宽度相差较大,为了清楚展示有限元模型,图5中改变了对称轴的实际位置。在实际结构中,膜盒一端与壳体环向焊接连接,另一端轴向自由移动,故在模型中将膜盒上下分别与两个压头tie约束连接,同时下压头底面设置边界条件ENCASTRE(U1=U2=U3=UR1=UR2=UR3=0)。首先开展网格无关性验证,针对不同的网格密度及网格类型进行模拟。结果表明,当模型单位长度(1 mm)内布种数超过30后,膜盒在全行程中的最大应力和最小应力幅值和分布已无明显变化(变化量不超过1%)。同时针对细化网格采用二次减缩积分单元与二次完全积分单元得到的模拟结果基本相同,但前者计算时间更短。因此,综合考虑计算效率和计算精度,每单位长度布置50个种子,即网格尺寸为0.02 mm×0.02 mm。网格类型选择二次轴对称四节点减缩积分单元(CAX8R)。金属膜盒模型共包括67 584个单元及215 063个节点。在上压头上端面分别施加向上17 mm和向下11 mm的位移载荷模拟得到膜盒在最大拉伸行程和最大压缩行程位置处的应力。

图5 金属膜盒有限元模型Fig.5 Finite element model of metal bellows
图6为金属膜盒在最大拉伸行程和最大压缩行程位置的应力云图。从图中可以观察到,膜盒在两个行程位置时的最大应力位置不同。当膜盒处于最大拉伸行程位置时,最大应力位于波谷弯角处(处);当膜盒位于最大压缩行程位置时,最大应力位于中部连接处(处)。上述两处位置(和)均为薄弱位置,需分别进行考虑。通过有限元模拟得到上述两处在膜盒全行程工作中的最大应力和最小应力,即
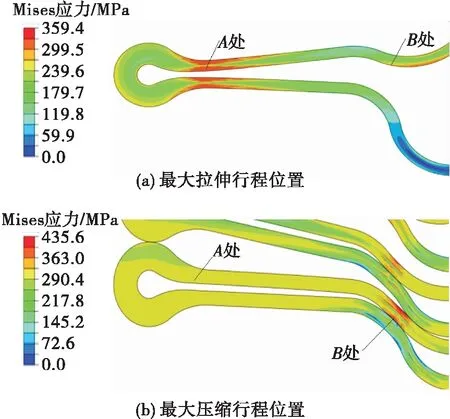
图6 金属膜盒应力分布云图Fig.6 Stress distribution of metal bellows
max=359 MPamin=-300 MPa
max=300 MPamin=-436 MPa
(13)
计算得到上述两处的循环应力参数(、和)为
a=(max-min)/2=329.5 MPa
m=(max+min)/2=29.5 MPa
=min/max=-0.84
a=(max-min)/2=382 MPa
m=(max+min)/2=-68 MPa
=min/max=-1.45
(14)
3.4 疲劳寿命N计算
对上述两个薄弱位置,将3.3节得到的两组循环应力参数(a、m、)、(a、m、)分别代入式(10)、式(11)、式(12)中,可计算得到相应的疲劳寿命。
波谷弯角处(处)疲劳寿命为
1=1.3×10/{1 556×329.5/[(1-0.84)×329.5+(1+0.84)×(778-29.5)]}=974
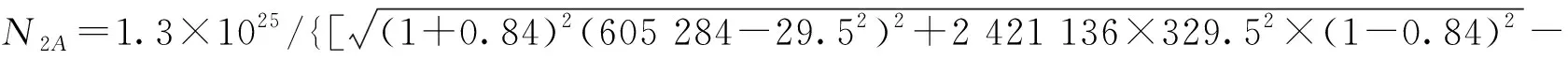
(1+0.84)(605 284-29.5)]/329.5×(1-0.84)}=990
(15)
3=1.3×10/{592×329.5/[(1-0.84)×329.5+(1+0.84)×(296-29.5)]}=966
中间连接处(处)疲劳寿命为
1=1.3×10/{1 556×382/[(1-1.45)×382+(1+1.45)×(778+68)]}=3 207

(1+1.45)(605 284-(-68))]/[329.5×1.45]}=3 299
3=1.3×10/{592×382/[(1-1.45)×382+(1+1.45)×(296+68)]}=3 083
(16)
针对波谷弯角处(处)和中间连接处(处)的疲劳寿命,可以观察到对于金属膜盒全行程工作,由Goodman模型、Gerber模型和Soderberg模型修正得到的3种广义——曲面计算得到的疲劳寿命基本相同。
通过对比波谷弯角处(处)和中间连接处(处)的疲劳寿命可以观察到,在金属膜盒全行程工作循环过程中,波谷弯角处(处)较中间连接处(处)疲劳寿命更少,最易发生疲劳断裂,进而造成膜盒失效。因此,针对该种形式的金属膜盒,需对该位置进行优化设计,同时在制造过程中确保此位置不应出现缺陷。
4 金属膜盒全行程疲劳循环试验验证
为了验证第3节中金属膜盒全行程工作时的疲劳寿命预测结果,按照3.2节中的几何尺寸制造了3件膜盒试验件,具体实物如图7所示。其中图7(a)为膜盒疲劳试验件整体结构,图7(b)为膜盒剖面。这里需要注意的是,考虑到上述3件膜盒试验件的制造成本和试验用途,并未对其进行解剖破坏。因此采用膜盒的工艺先行件剖面进行展示[见图7(b)]。该剖面状态并非膜盒初始位置,同时由于首件工艺不成熟,其几何尺寸与设计状态偏差较大。实际的3件膜盒试验件对工艺进行了优化,以确保几何尺寸与设计状态保持一致。

图7 金属膜盒Fig.7 Metal bellows
对上述3件膜盒试验件按照→→的全行程进行疲劳循环试验。试验过程中,循环速度3次/min,通过加卸压方式实现。最终3件膜盒试验件疲劳循环次数分别为1 368、1 291、1 346,同时失效位置均在膜盒的内波谷处,如图8所示。

图8 金属膜盒疲劳失效位置Fig.8 Fatigue failure position of metal bellows
通过广义的疲劳寿命预测模型和试验得到的膜盒疲劳寿命及失效位置对比如表3所示。

表3 有限元模拟与试验结果对比Tab.3 Comparison of finite element simulation and experimental results
从表3可以看出,试验疲劳寿命略高,考虑到实际金属膜盒成型工艺和加工的影响,可以认为试验结果与预测结果基本吻合。这表明,通过修正后的广义——曲面可为金属膜盒循环工作的疲劳寿命提供一个略保守的预测结果。
5 金属膜盒非全行程循环工作疲劳寿命预测
金属膜盒不仅应用于推进剂补加系统,还应用于金属膜片贮箱温度交变补偿系统。由于金属膜片贮箱工作时金属膜片始终紧贴推进剂液面,空间温度变化引起的推进剂体积变化会造成金属膜片承受交变载荷。通过金属膜盒贮箱可有效对上述推进剂体积变化量进行管理,避免金属膜片发生疲劳失效。此时的金属膜盒为若干平衡位置处的小行程循环工作。因此,本节针对某型号飞行器补偿膜盒贮箱,通过广义——曲面分析第4节中制造的膜盒能否满足温度交变补偿的任务要求。
通过对该飞行器任务剖面分析,得到该膜盒主要工作状态为在两个平衡位置(=10 mm、=26 mm)分别进行50 000次上下5 mm的小行程循环,要求工作中膜盒不发生泄漏。
首先通过有限元仿真计算得到膜盒在上述两个平衡位置处的小行程循环的、和。
位置处参数为
=40 MPa=173 MPa=0.62
(17)
位置处参数为
=11.5 MPa=-421.5 MPa
=1.06
(18)
采用3.1节中基于Goodman模型修正的膜盒广义--曲面[见式(10)]对上述两个位置的循环寿命进行计算,得出
=95 960=5 620 476
(19)
在位置循环应力作用一次的损伤量(1)=1/=1/95 960;在位置循环应力作用一次的损伤量(1)=1/=1/5 620 476。
该膜盒在整个非全行程循环后的损伤量为
=(50 000)+(50 000)=/+/=50 000/95 960+50 000/5 620 476=0.53
(20)
<=1,因此膜盒在该非全行程循环后不会发生泄漏。
6 结论
1)由Goodman模型、Gerber模型和Soderberg模型修正得到的3种广义--曲面对金属膜盒的疲劳寿命预测结果基本相同。
2)通过修正后的广义--曲面可对膜盒循环工作的疲劳寿命提供一个略保守的预测结果。
3)对于本文中的无缝金属膜盒,内波谷弯角处为薄弱环节,实际应用中需针对该位置进行优化设计,同时在制造过程中确保此位置不应出现缺陷。
