涡轮叶片U型冷却通道旋转流动特性模拟
2022-07-07吴传伟宋江涛
丁 旭, 吴传伟, 刘 涛, 宋江涛
(1.中国航空工业集团有限公司 中国飞行试验研究院,陕西 西安 710089;2.哈尔滨工业大学,黑龙江 哈尔滨 150001)
0 引言
随着现代军备的日益发展,各国都在竞相发展航空工业,航空领域的竞争也越来越激烈,世界各强国对航空发动机技术提出了更高的要求。根据热力循环分析,航空发动机设计工程师致力于提高发动机涡轮前温度,以提高航空发动机的推力。根据计算,同一发动机涡轮前温度每增加55 ℃,发动机可增加大约 10% 的推力。随着对高推重比发动机发展需求的增加,发动机涡轮前温度也越来越高, 这就需要对涡轮叶片恶劣工作环境进行评估。为了解决这个问题,通常有两种工作方法:① 开发新材料以提高叶片材料的耐热性;② 采用先进合理的冷却方式以获得更好的冷却效果。其中采用U型冷却通道的叶片冷却技术属于新兴技术,被广泛研究。
在发动机开发过程中,受限于材料技术的发展,叶片耐热性的提高速度远远不能满足提高航空发动机涡轮前温度的需求。因此,采用合理而先进的冷却方法来冷却叶片是解决这个问题的最重要方法。苏联火箭专家齐奥尔科夫斯基提出的再生冷却方法是一种先进合理的冷却概念,在高超音速领域得到广泛应用。它的主要原理是,通过液态烃燃料流经发动机的高温部件,从而进行冷却,同时,高温使大分子碳氢化合物燃料分解并转化为一系列小分子,然后进入燃烧室燃烧,带来热防护的同时也带来了热循环优势。
常用的叶片冷却方式主要包括叶片的表面冷却和内部冷却。内部冷却主要分为直流通道、转弯通道和其他通道。作为叶片内部冷却的关键技术,管道内部冷却是目前研究的热点。作为旋转部件, 旋转条件下内部管道的传热性能和流动特性的研究将为旋转机械在工程中的应用提供强有力的理论支持。Liou等研究了180°平滑双通道中的流动基础。Johnson等通过对蛇形管内流动的实验研究,得到了旋转状态下的传热规律,提取了相关的经验公式,为后续叶片设计和叶片冷却提供理论依据。以上研究均致力于叶片内流动通道在旋转条件下的传热特性研究。旋转管道的流动与传热特性的研究对旋转机械在工程上的应用提供重要的理论支持。旋转管道内的流体在流动过程中受到管道曲率与挠率的影响,同时受到科氏力的作用,与静止管道流动相比,非线性效应更加突出,横截面上将出现形态复杂的二次流,在某些条件下将出现分叉流动现象。为了简化研究方法,研究碳氢燃料在旋转条件下冷却通道内的换热特性,并便于计算,同时更加符合实际情况,本文构建了旋转条件下矩形截面 U型冷却通道的计算模型,对典型工况下的流动进行了计算和分析,揭示了其传热规律。
1 数值计算方法
1.1 计算模型
图1所示为矩形截面U型冷却通道的模型图。整个矩形旋转通道分为U型通道的进口段、U型通道的水平段和出口段。通道的横截面是方形的,横截面的边长是4 mm,4个面分别是前端面、后端面、外侧面和内侧面。整个U型通道的径向长度为40 mm,弦长为20 mm。管道入口与旋转轴之间的距离为100 mm,整个通道的平均旋转半径为120 mm。

图1 U型冷却通道模型图Fig.1 Model diagram of U-shaped cooling channel
本文的计算网格使用ICEM生成,为了保证计算精度,根据湍流模型要求,使冷却通道壁面边界层<1,通过计算调整,选择流体域内壁面第一层网格高度为0.002 mm,设置增长率为1.1。为保证网格达到计算精度,对网格进行无关性验证。图2所示为计算结果收敛性分析,当网格数量达到1.75×10时,模型收敛程度以及计算结果误差值均满足计算精度要求。

图2 不同网格方案收敛情况Fig.2 Convergence of different grid schemes
1.2 计算方法和边界条件
本研究采用Fluent中的双精度速度压力耦合求解算法,湍流模型是-SST模型,能量项采用QUICK模型,压力动量项和密度项计算采用二阶逆风差分格式。计算域的边界条件设置如下:U型通道的入口是质量流入口,给定一定质量流的正癸烷,燃料温度为390 K,热边界条件为均匀热流密度。为保证计算符合实际使用情况,出口条件设置为压力出口,压力为4 MPa,并且计算流道内正癸烷为超临界条件。考虑到叶片在实际工作中受到高温的影响,且叶片内部为U型旋转冷却通道结构,整个系统的边界条件可以假设 U型冷却通道的4个壁都受到热负荷的影响,即

(1)
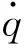
1.3 计算方法验证
据文献[19]的旋转试验研究,验证了计算方法。选择=0.52 时的旋转情况,定义惯性力和科氏力的关系,表示转速的大小,如图3 所示。
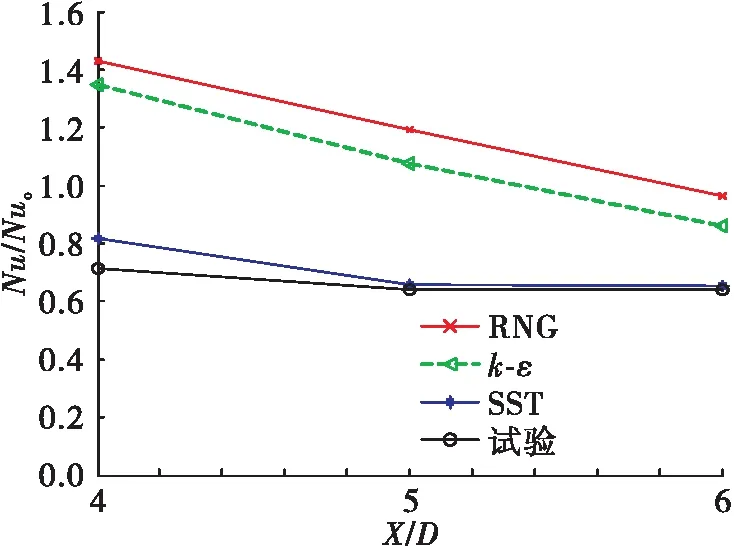
图3 湍流模型验证Fig.3 Validation of turbulence model
横坐标为管路沿程长度与直径之比,即其当量直径。可以看出,在旋转流场的计算中,选择 SST 模型,其计算结果趋势接近,这与试验结果值最一致,能够作为可信赖湍流模对该论文课题情况进行计算。
1.4 数据处理方法
由于超临界流体的物理特性很容易受到其温度和压力的影响, 在流动和传热过程的计算中,需要选择一个能充分反映所研究物质特性的参考值,作为物理性质计算的标准值。如式 (2) 所示,采用了一种计算流体横截面平均温度的方法, 对流传热系数和努希尔数用于评估传热特性,如式(3)所示和式(4)所示。

(2)
=-
(3)

(4)
式中:为计算截面处的壁面均温,K;为计算截面处的流体均温,K;为计算截面表面处沿程传热系数,W/(m·K);为通道的特征长度,m;为计算截面的平均热导率,W/(m·K);为努希尔数。
2 计算结果及分析
在以往的文献研究中,工作介质为空气时的热流密度一般为2 000~6 000 W/m,考虑到高超声速场, 碳氢燃料的热流密度一般可以达到 2~4 MW/m。综合考虑模拟需求,研究中的热流密度设定为 0.2 MW/m,不仅能满足涡轮冷却需求, 同时也充分考虑碳氢燃料的传热潜力。给定的碳氢燃料质量流量为 10 g/s,工作压力为 4 MPa。为了保证U型换热通道内的流体能够正常流动,考虑到本研究中的最大转速为 1 500 r/min, 只需要确保最大旋转离心力不大于工作压力。表1列出计算的边界条件。

表1 边界条件Tab.1 Boundary conditions
前人有关转速对流量的影响做了大量的研究,主要集中在空气在 U型管道中的流动特性。为了进一步研究碳氢化合物燃料在旋转条件下U型管道中的流动特性,首先, 进行固定工况下的流动分析,研究管道内的流动特性和二次流的发展。为了便于分析,选择U型通道的横截面,如图4所示。
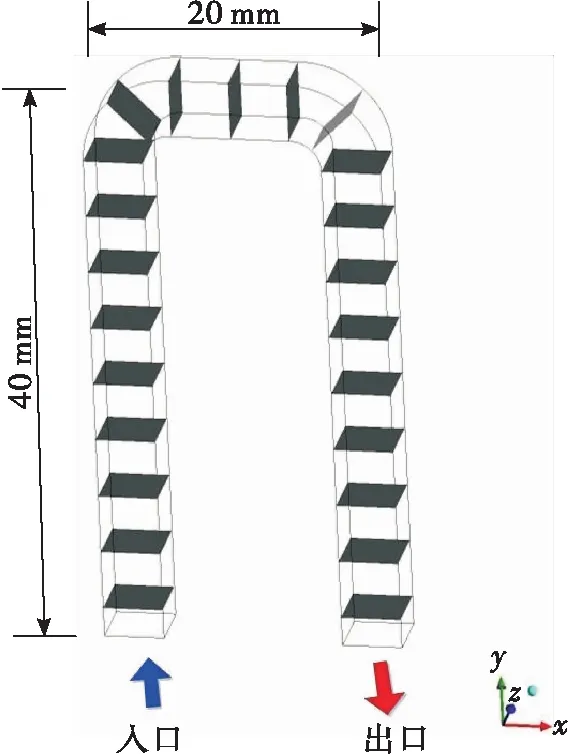
图4 U型通道截面分布图Fig.4 Distribution of U-shaped sections
从=0.5 的位置取径向直管截面, 沿方向依次取横截面,间隔为 1,在弯曲角度的中间 45°的位置再取一截面。横向段从弯管结束开始每隔=1取一个截面,即位置依次为6 mm、10 mm、14 mm。下面将详细分析旋转条件对碳氢化合物燃料在进口段、横管段和出口段流动的影响。
2.1 进口段流动性能
图5为进口段流线示意图,横坐标方向是U型管通道的方向,纵坐标方向是U型管的方向,左侧是外侧,右侧为内侧。可以看出,在静态状态下,U型管道中的入口流以射线的形式对称分布,从流线看出,没有产生涡流,并且受到壁边界层的影响,U型管内的流动有从壁角向壁中心、从壁向流道中心收敛的趋势。随着流动的发展,流体越来越收敛到弯管,受拐角曲面的影响,流动中心接近弧形内壁。

图5 进口段流线图Fig.5 Streamline diagram of inlet section
旋转角速度为 1 500 r/min 时,在初始入口截面的横截面上,科氏力作用还不明显,并且管道横截面中的流动仍然由壁边界层效应主导,流动集中在重壁到流动通道的中心。与静态条件相比,主流中心从后边端表面偏移。随着流动的发展,科氏力对流动中心的影响逐渐增强,并且由于壁面位置的径向速度比流动通道的中心小得多,流动通道中心的科氏力更加明显,这导致中心流从前端平面流向后端平面的趋势,而后端平面流向前端平面的趋势出现在墙面,然后在横截面上形成两个对称的涡流结构,涡流中心也移动到前端表面。流体继续向下游径向发展。当旋转管道前端面一侧的浮升力大于旋转离心力时,前端面一侧流体产生回流现象,于是出现同一通道内流体相对流动的现象。虽然前端面一侧的回流流速远小于主流,但是仍然受到科氏力的影响,因此,在此时,流道截面在两个对称的主涡流内部分别出现两个涡流中心。一个涡流中心是主流在科氏力的影响下产生的,靠近后端面,另一个涡流中心为回流的涡流中心,靠近前端面。回流区涡流详细路径如图6所示。从图中也可看出前端面温度较高,梯度也大,受浮升力影响较大。

图6 1 500 r/min时进口管道l/D=6.5截面流线图Fig.6 Sectional streamline of inlet pipe with l/D=6.5 at 1 500 r/min
2.2 横管段流动性能
U型管通道的水平截面的横截面流线图如图7所示。在图中,横坐标方向是U型管通道的方向,纵坐标方向是U型管的方向,左侧是外侧,右侧是内侧。从图中可以看出,在水平剖面上,出现了弯头的Dean涡旋现象。在静态条件下,主要是弯管的 Dean 涡产生的二次流。在45°角处,沿U型管的方向形成两个对称的涡流结构,流线从内侧流向外侧,然后在前端面和后端面靠近墙面的位置产生涡流中心。旋转90°弯头并进入水平段后,流线从内侧的中心流向外侧,然后在前端和后端附近形成涡流中心,此处涡流中心的强度大于45°角处的强度。随着流动的发展,涡流中心从两侧向中心转移。

图7 横管段流线图Fig.7 Streamline diagram of horizontal pipe section
U型通道角速度为1 500 r/min时,流体将受到肘部和旋转的共同作用的影响。在科氏力、离心力和惯性力的共同作用下,与静态相比,通流中心的两个对称 Dean 涡流发展成为涡流中心,流体以螺旋形向前移动,旋转中心更靠近后端面,这使得这部分的流动最复杂,湍流度也高,热交换最强。然而,由于主流的螺旋推进,圆周热交换有很大差异。
2.3 出口段流动性能
如图8所示,对于U型通道横管截面所在的截面,该截面是流线型的。在静态条件下,由于管道弯曲效应,出现了 Dean 涡流现象。然而,由于上游流对第二弯头的影响,第二弯头后的主流流更加复杂,大致形成了4个涡旋中心,包括靠近外侧的两个较大的漩涡和靠近内侧的两个较小的漩涡。4个涡流中心相互作用并随水流发展,出口部分形成复杂的二次流, 以两个对角线涡的外侧壁上的大涡为源,形成一个大涡绕流再到对角线涡,如图9所示。随着流动的继续,在出口部分,流动趋于平坦。

图8 出口段流线图Fig.8 Streamline diagram of outlet section

图9 静止状态下出口段l/D=17.7 处截面流线图Fig.9 Sectional streamline at outlet section l/D=17.7 under static state
当旋转角速度为 1 500 r/min 时,在肘部效应、离心力和科氏力的共同作用下,出口端内部流动趋向于前端面,并且前端面的压力比较大,也就是说,流体对前端面的冲击更加严重,使其换热效果比后端面的更强,这与进口管段的规律相反。旋转条件下浮力的作用是科氏力使流体温度扩散得更快,离心力引起的浮力与主流方向一致。如图9所示,为静止状态下出口段流线图,水平段涡流效应引起的流体的螺旋正向效应仍然影响出口段的流体,科氏力影响它,涡流中心作用在 U型管的后端面和内侧的对角线上。旋转状态和静止状态的区别在于在静止状态下形成了4个强度相似的涡流中心,但是在旋转状态下形成了一个占据整个横截面的涡流,并且有一个小涡流嵌入大涡流中。与进口段相似,旋转引起的科氏力使流体向一侧倾斜,但出口段的二次流更复杂,湍流水平更加强烈。图10为横管段不通旋转工况条件下沿程对比,整体看来,横端面换热效果随着转速的增大有较大的提高,可以看出,旋转条件下由于二次流的原因,其换热能力增强。

图10 不通旋转工况条件下沿程Nu对比Fig.10 Comparison of Nu along the way under no rotation condition
3 结论
本文对发动机涡轮叶片 U型冷却通道的液冷传热进行了研究。采用 Fluent 中双精度速度压力耦合求解器的简单算法,湍流模型采用-SST模型,压力动量项和密度项用二阶迎风差分格式数值计算,能量项用快速格式计算,实现了旋转条件下U型冷却通道内流动的数值计算。主要结论如下:
1)与静态相比,旋转使 U型换热通道中的流动更加复杂,湍流度更强。
2)高速旋转时,U型通道内径向流出流体有一个从 U型通道前端到后端的流动趋势。当转速足够高时,会出现回流现象,后端面的换热效果比前端面更强,这表明回流增加了湍流程度,提高了热交换能力。
3)径向流入段的流体有从 U型通道后端到前端的流动趋势,所以前端的传热比后端的传热更强,这与径向流出定律相反。
4)在水平段,两层旋转力和 Dean 涡是由旋转引起的,其传热性能最强。
