浅谈空间傅里叶“变”换之“变”

刘可心

摘要：随着5G技术的崛起，智能信息处理技术进入新高速发展时期，通信领域对信号处理技术提出了新要求。作为信号处理领域的基本工具，傅里叶分析重要性自然不言而喻。其不仅存在于信号与系统、通信原理等多门专业课程中，同时对诸多学科的研究提供理论贡献。但学习过程中总令学生产生不懂概念，死记硬背的现象。为了避免此现象，本文主要内容如下：从空间角度，结合现有课本中矢量空间类比到信号空间的思路，带学生领略不一样的傅里叶“变”换，真正理解何为“变”，如何“变”，以及“变”的本质和“变”的应用范围。

关键词：傅里叶变换;信息处理;矢量空间;信号空间

1傅里叶变换

1.1 “变”的重点和难点

首先，谈谈为何“变”，傅里叶变换的研究重点是如何将信号表示为一系列正交函数的组合;如何由矢量的正交分解转向信号的正交展开;如何从傅里叶级数延伸到傅里叶变换。但在理解细节的时候存在着诸多难点，比如为何要表示为正交函数;为何常引入误差变函数表达。为了理解重难点，我们亟需“变”，即寻找高效的理解思维来加深我们对傅里叶分析的认知。

1.2 傅里叶分析的新视野

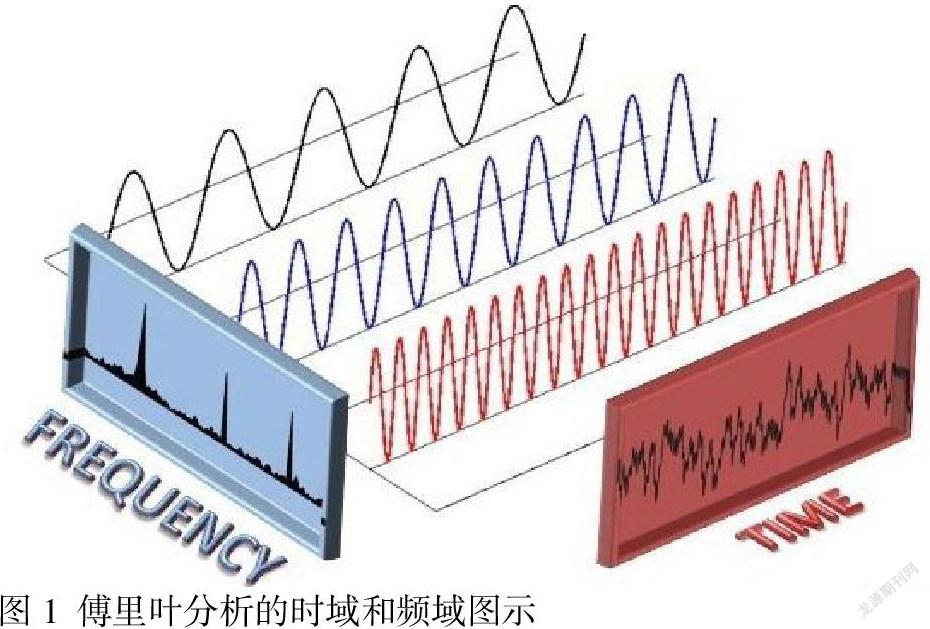
其次，看看什么是“变”。俗话称“穷则变，变则通，通则久”，一门课程，当遇到难点、困难时，需要我们跳出已有维度，用更大的格局来看，这就叫做“变”。同样，傅里叶作为分析信号分解的重要工具[1]，这种“变”，就是空间理解。傅里叶所一直追寻的正是元素间所具备的某种规律关系的数学表达形式，从时域跳到频域，如图1所示，化复杂問题简单化，这种思路与探究空间傅里叶表示是有所共鸣的。

2.矢量空间、信号空间与正交分解

接着，谈谈如何“变”。傅里叶空间分析有助于我们对细节的把握。平面几何，立体几何，这就是直观的空间，相应xy轴二维坐标，xyz三维坐标正是空间里任意元素的度量表示。加入时间维度后就是四维空间，使我们能更细致的表示所在空间中的事物。可见基于空间分析的重要性。

2.1 空间的衡量与表示

总结以上实例，不难发现，元素和规则构成空间。矢量、函数都可以视作空间中的元素;线性的概念“利用一组基，使用加法和乘法来表示所有的元素”[2]就是规则。借助空间载体，结合规则后，才能实现任意元素在空间中的度量和表示，进而分析元素间关系。以二维坐标表示平面向量为例，坐标对应基底，向量对应元素，平面上待表示的任意一点，就是坐标。随着科学探索不断深入，维度不断增加，科学家已经提出了11维宇宙空间，这种情况下，代数关系式不再适用，需要依托更精准的空间来表示高维抽象事物。

为了实现高维空间度量，这里引入的三个衡量指标：距离、范数和内积[3]，以便理解其对应的三个空间。距离就是衡量两种元素之间的相似度，值为0时二者为同一事物，其公式用（1）表示。

范数（2）是对矢量本身长短进行度量，是更具体的一种规则，其可以通过（3）式来定义距离。

值得一提的是二范数，即p=2时，常用其来约束矢量、函数，使其拥有与目标距离无限接近的最小误差，起到防止过拟合的优化作用，例如星座图、误码率等概念都。而这里提及的最小误差，为之后理解傅里叶变化中的信号空间大有裨益。

内积是为了丰富上述概念，引入角度的点积操作，如（4）式，类似可用（5）式导出其范数。

而这三个概念对应的线性空间分别为：度量空间、赋范空间和内积空间。重点选用内积空间，有助于在特定变换下维持空间中的向量不变性。下面沿用矢量空间到信号空间的类比学习思维。针对矢量空间，在内积空间的基础上引入复数域，得到酉空间，深入理解离散傅里叶变化;针对信号空间，在酉空间的基础上增加维度，得到希尔伯特空间，深入理解连续傅里叶级数和傅里叶变化。

2.2 矢量空间与信号空间

“变”的本质就是在合适的内积空间里寻找基底来表示元素。傅里叶变换的研究目的即将信号分解为一系列正交函数的组合。而这种组合就是选择基底的表示并计算坐标（傅里叶系数）的过程。

先看矢量，以酉空间为载体，针对任两组矢量，其夹角可以表示为（6）。

（7）式是两个矢量的夹角表达式，分子是内积，分母项为范数。为90度时，两矢量垂直，内积值为0，此时正交，其本质是x在y上的投影。那么可以用这两个矢量视作基底，来度量任意向量。

推广到N维后，出现线性表示形式（8）、基底的正交性（9）及坐标表示过程（10），即投影系数。

再看以希尔伯特空间为基底的信号空间，类比于矢量空间，找到基底（11）。

引入误差函数，并假定其无限趋于0时，所构造信号是原本信号在基底函数所构建信号空间中的投影，投影系数表示为（13）。

3.空间傅里叶变换的深入理解

在1、2基础上，将离散傅里叶变换放在矢量空间分析，将连续傅里叶级数和傅里叶变化放在信号空间分析，很快得到空间中的表现形式：离散傅里叶变换其基底（14）、并构造出其变换表达

4.小结

本文从空间的角度重新深入理解并认识了傅里叶分析，发现相比于课本上的公式推导，这种思维可以化复杂为简单，更换思考问题角度，以更多视角认知问题，进而将其运用在交叉学科中，有所收益。

参考文献

[1]朱宁贤.基于MATLAB的傅里叶函数变换可视化分析[J].办公自动化，2020，25（05）：20-22.

[2]郑前前，杨文杰，岳晓鹏.基于线性代数矩阵理论的“学”与“用”[J].黑龙江科学，2022，13（01）：110-111.

[3]（美）艾伦.V.奥本海姆（Alan V. Oppenheim），（美）艾伦.S.威尔斯基（Alan S. Willsky），（美）哈米德.纳瓦卜（S.Hamid Nawab）著;刘树堂译. 信号与系统（第二版）[M]. 北京：电子工业出版社，2020.8