聚驱后水驱油藏层间窜流试井曲线特征1
2022-07-06瞿朝朝刘宗宾王欣然刘斌张振杰
瞿朝朝,刘宗宾,王欣然,刘斌,张振杰
(中海石油(中国)有限公司天津分公司,天津 300459)
A油田位于渤海辽东湾海域,具有高孔、中高渗储层物性特征,油水井间距大,储层纵向非均质性强[1,2]。油田实施早期注聚,取得了一定的降水增油效果,目前为后续水驱阶段,经过长时间的开发地下渗流情况变得异常复杂[3-7]。有关不同驱替介质复合油藏试井和多层油藏层间窜流试井国内外学者已有一定研究,如Lund等[8]得出了非牛顿流体在复合油藏中渗流的双对数曲线特征;宋考平等[9]开展了非牛顿-牛顿复合油藏渗流试井问题研究;郭辉等[10]对聚驱复合试井模型进行了研究;霍进等[11]提出了多层窜流油气藏模型;贾永禄[12]分析了具有窜流的双层油气藏井底压力动态模型等,但同时考虑不同驱替介质和层间窜流叠合影响的试井模型较少。由于同时考虑两者影响,使得海上聚驱后水驱油藏层间窜流试井模型的建立和求解非常复杂。本文基于渗流力学理论,重构了描述层间窜流及平面非均质性的数学模型,建立了聚驱后水驱油藏层间窜流牛顿-非牛顿复合试井新模型,运用有限差分算法计算求得不同小层井底压力的瞬时解,并绘制出试井双对数理论图版,旨在为海上该类油藏的试井解释提供理论指导。
1 物理模型建立
层间窜流模型考虑条件:(1)考虑油藏中的某开发井包含两层储层,其注聚结束后进行水驱,存在窜流,如图1所示。各层流体性质相同,注入量一定。(2)考虑内区流体为水相,可视为牛顿流体;外区为聚合物溶液,可视为非牛顿流体,且均为微可压缩流体。(3)两区流体满足达西渗流,渗流过程温度不变。(4)不考虑重力、毛管力。(5)
两区渗流交界面不考虑附加压力降。(6)考虑井筒储集效应和表皮效应。
2 试井模型建立及求解
2.1 数学模型
牛顿-非牛顿复合模型内区驱替介质为水,外区驱替介质为聚合物溶液,基于上述模型,以渗流力学基本理论为指导,建立基于层间窜流“凹子”特征的聚驱后水驱牛顿-非牛顿复合试井解释数学模型。
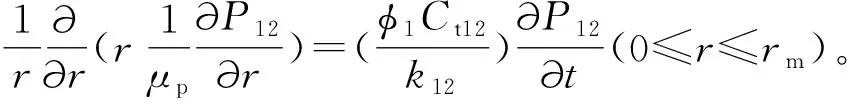
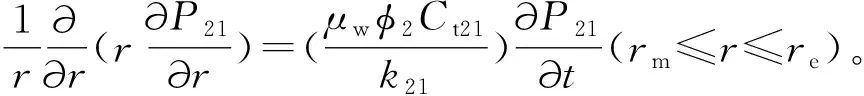
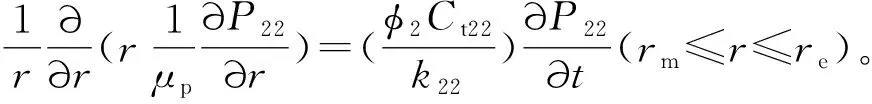
(2)初始条件。P11(r,t=0)=P12(r,t=0)=P21(r,t=0)=P22(r,t=0)=Pi。式中:Pi是原始地层压力,MPa。
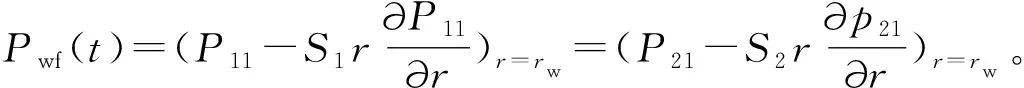
(4)外边界条件。P12(∞,t)=P22(∞,t)=Pi。
2.2 模型求解
基于油藏实际情况,模型考虑了储层间的窜流特性及聚合物溶液的剪切、扩散、对流等非牛顿特性,渗流方程变得异常复杂,导致利用常规解析方法求解较困难,本文通过有限差分算法进行时空网格划分求解方程组,从而得到各层井底压力的瞬时解。
(1)渗流差分方程。1-1区:
(1)
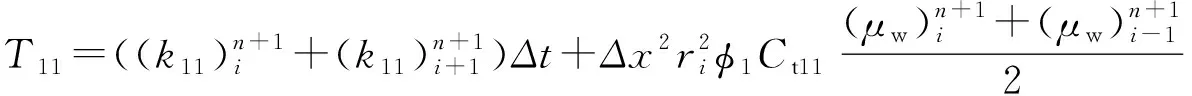
(2)
式中:i为对空间的离散,i=1,2,…,N;n为对时间的离散,n=1,2,…,K;Δt为离散时间步长,h;Δx为离散空间网格大小,m。
1-2区:
(3)
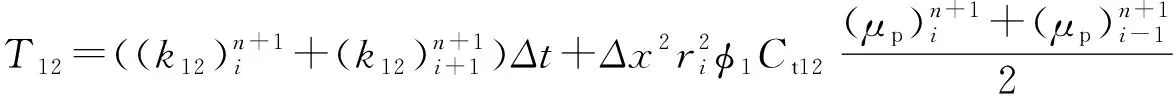
(4)
2-1区:
(5)
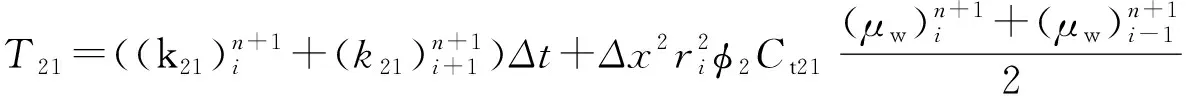
(6)
2-2区:
(7)
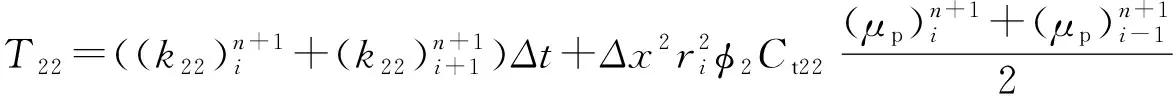
(8)
(9)
(3)内边界条件。第1层内边界:
(10)
第2层内边界:
(11)
(12)
(5)界面压力、流速相等条件。第1层:
(13)
第2层:
(14)
式中:I为两区交界面处位置。联立式(1)~(14),可得井底压力随时间的变化式:
(15)
3 导数曲线特征分析
根据文中建立的层间窜流模型,运用有限差分算法迭代求解可得考虑聚合物非牛顿影响的试井曲线图版,见图2。从图2可看出双对数曲线包括6个特征阶段。阶段①中,压力曲线和压力导数曲线基本重合,且斜率均为1,此阶段为井筒续流阶段;第②段是过渡流阶段,导数曲线呈“驼峰”状;第③段为流体从低流度层向高流度层的窜流段,压力导数曲线出现“凹子”特征,“凹子”深度与流度差异相关;第④段为内区拟稳定段,内区流体窜流达到拟稳定状态,导数曲线在纵坐标上值为0.5;第⑤段为水相到聚合物溶液的过渡段,表现出聚合物驱后实施水驱开发的复合特征,曲线呈抬升状,抬升幅度与外区聚合物质量浓度相关;第⑥段为内外区共同作用阶段,受外区聚合物溶液非牛顿特性的影响,压力导数曲线表现出小幅度上翘。
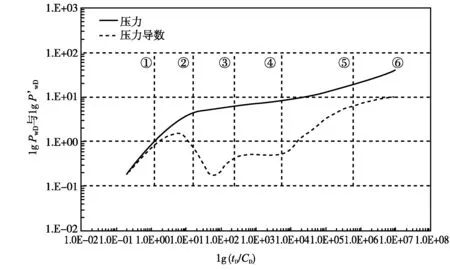
图2 层间窜流牛顿-非牛顿双对数曲线图版
通过唯一变量法研究流度比、聚合物质量浓度对双对数曲线形态的影响,见图3、图4。
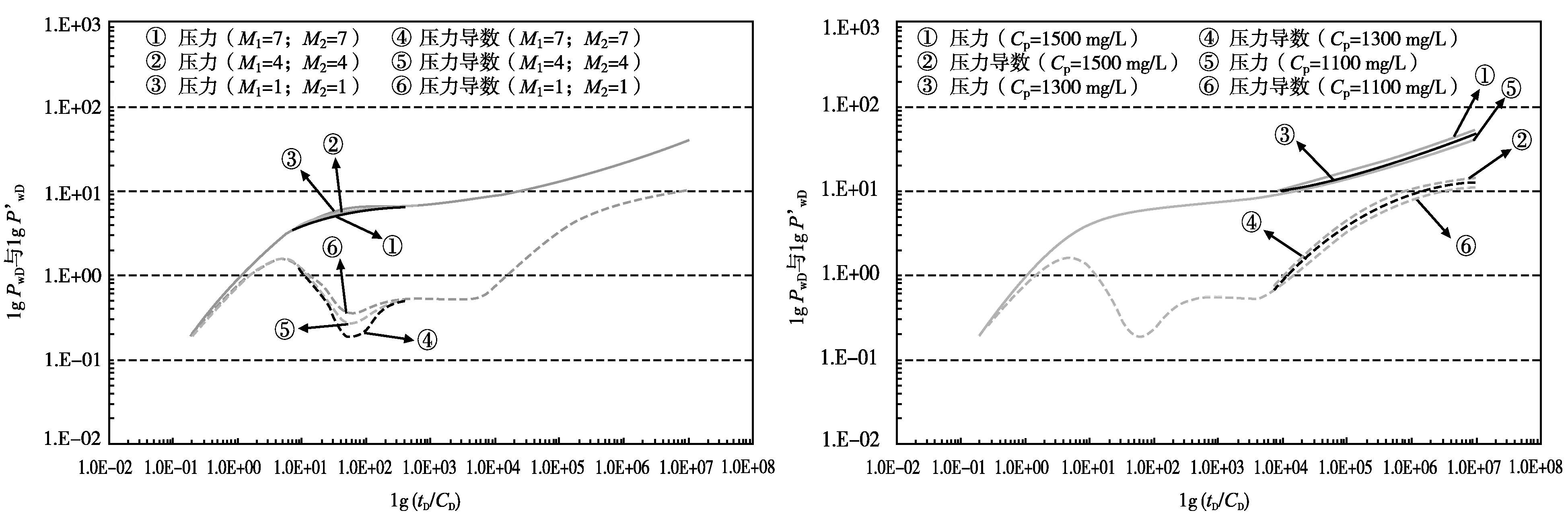
图3 流度比对导数曲线影响 图4 聚合物溶液质量浓度对导数曲线影响
图3反映2层流度比对双对数曲线的影响。从图3中可以看出,2层流度比对“凹子”下凹深度影响较大,2层流度比越大,高低流度层渗透率差异越大,压力导数曲线“凹子”越深。图4反映了聚合物溶液质量浓度对导数曲线的影响。从图4中可以看出,聚合物溶液质量浓度对水相到聚合物溶液的过渡段影响较大,聚合物质量浓度越高,对应的聚合物溶液黏度越大;流动性越差,导致过渡段抬升幅度越大。
4 现场应用实例
渤海A油田注聚井X1射开层位为东营组Ⅱ-2、Ⅱ-3小层,2017年底该井停注聚后周边生产井X2井含水上升,生产形势变差。针对该问题,于2018年9月对X1井进行压降测试,X1井相关静态参数如表1所示。选择常规解析模型对X1井进行试井解释,拟合曲线如图5a所示,曲线未能反映出层间窜流的“凹子”特征及聚合物溶液的非牛顿特性;采用文中描述层间窜流及不同驱替介质的双对数图版拟合情况如图5b所示,拟合程度高,试井解释动态参数为:k11=1500×10-3μm2、k21=214×10-3μm2、k12=310×10-3μm2、k22=44×10-3μm2,解释结果与测井解释及油藏动态认识相符。诊断X2井含水上升生产形势变差原因为,高低渗透层层间窜流导致层间干扰加剧,形成优势渗流通道。2018年12月对X1井第1层挤注调剖主剂和交联助剂后,周边受效采油井X2由调剖前日产油17 m3,含水92%,变为调剖后日产油64 m3,含水68%。X1井调剖前后,采油井X2井高峰日增油47 m3,含水下降24%,有效缓解了停注聚后该井的含水上升,如图6所示。目前应用该方法在渤海聚驱后水驱油藏成功指导10余井次压降测试资料解释,治理了多口低产低效井,取得了不错的降水增油效果。
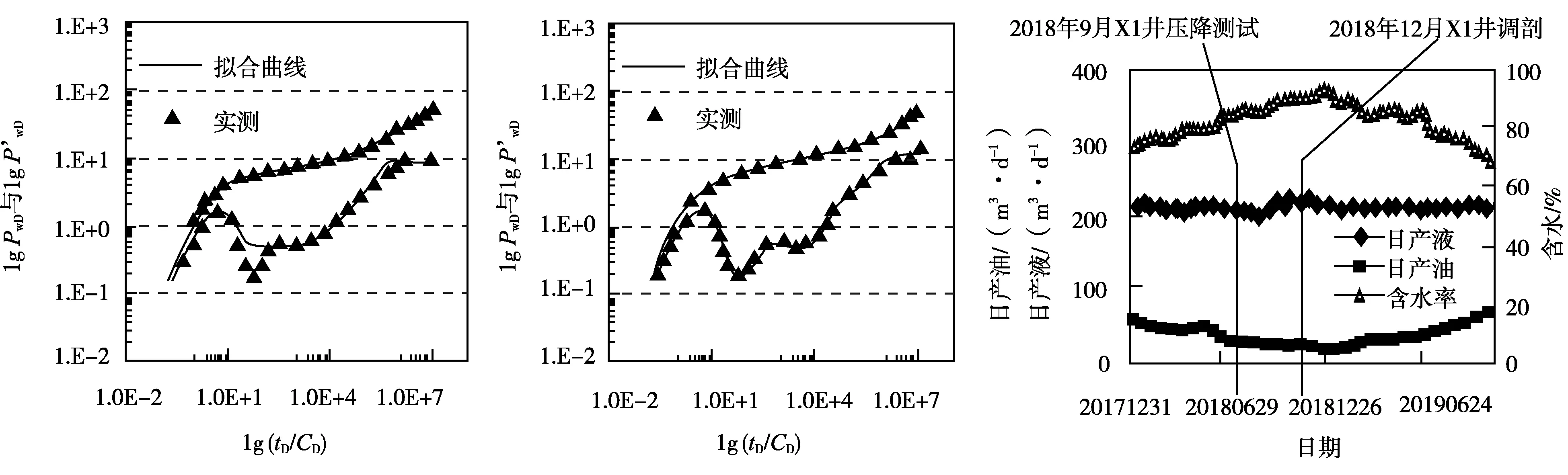
a 实测数据与常规解析模型拟合曲线 b实测数据与本文图版拟合曲线图5 实测数据与2种模型拟合结果对比曲线 图6 X1井调剖前后对应受效井X2井影响

表1 X1井静态参数第2层地层厚度/m第3层地层厚度/m井半径/m体积系数/f孔隙度/%原油黏度/(mPa·s)综合压缩系数/MPa-129.920.80.121.120.29140.0014
5 结论
(1)流度比、聚合物质量浓度对双对数曲线特征影响较大,2层流度比越大,压力导数曲线“凹子”越深;聚合物质量浓度越大,水相到聚合物溶液的过渡段抬升幅度越大。
(2)利用该模型对现场实例井的压降测试资料进行解释,依据解释结果成功指导油田低产低效井治理5井次,提高了区块采收率,产生了较好的经济效益。
