内部充水钢围堰的结构安全稳定分析

张 羽 ，赵集云 ，刘明潇 ，孙东坡

(1.华北水利水电大学 水利学院，河南 郑州 450046； 2.华北水利水电大学 水力学及河流研究所，河南 郑州450046)

大型输水干渠大多为跨流域调水工程，多采用明渠输水形式。长距离、大型输水干渠受运行工况限制，一般没有停水维修的条件，运行期渠道维修只能在输水状态下进行。南水北调中线总干渠担负着沿线调水、供水的重任，维修更是不能影响正常输水。为了满足不停水开展渠道修复，在需要维修的渠道一侧边坡设置钢结构的“围墙”（即钢围堰），与边坡一起构筑成与渠道水流既相对连通又相对封闭的静水施工环境。这样的钢围堰设置既容易平衡渠道水流的动水压力，又为渠道边坡修复提供一个可靠的静水施工环境，很好地解决了大型渠道输水状态下的边坡修复难题。

与传统钢筋混凝土工程相比，钢结构安装精度较高，轻便易运输，同时其整体稳定性也需要得到一定的保证。左丽等[1]设计了一种自平衡组合式挡水围堰，研究了挡水面板、支撑传力系统，并进行了有限元分析，但围堰的最大吃水深度只有3.0～3.5 m，无法在南水北调总干渠水深8 m处进行作业。王岩松[2]设计了一种水中下放升降平台，工作完成以后，抽出舱内水，利用水的浮力使围堰上浮，最后对围堰切割拆除。但是这种双壁钢围堰入水时需要大型机械运送，空间会受到限制，而且在拆除过程中难度大，切割成本高。郭海亮等[3]提出将钢模板围堰从安装到下水固定的整套理论，钢围堰采用装配式结构，首先在一级马道上进行焊接拼装，然后由牵引装置牵引下水，再经过模板固定，混凝土浇筑，结构缝处理等步骤将钢围堰整体稳定；武法聘等[4]采用MIDAS/Gen 800建立有限元模型对围堰进行分析，得到了立柱式、桁架式围堰结构的最不利应力分布形式；钟祺等[5]对多种围堰进行对比分析，通过MIDAS Civil软件对围堰进行设计和验算，最后通过多种工况分析，验证了优化后的结构满足规范要求。黄鑫伟等[6]采用Fluent有限元软件，模拟了钢围堰设置对航道水流条件的影响。

本文以南水北调中线总干渠辉县段渠道为典型工程，利用现场水深流量监测数据，通过数值模拟ANSYS软件，计算出两个流量条件下围堰的受力和变形情况，分析钢围堰上游、中游及下游的刚度、强度和稳定性，并提出结构优化调整等改善措施，以期有效解决围堰施工问题。

1 钢围堰工程简介

南水北调中线一期工程总干渠明渠段结构型式为梯形断面混凝土衬砌，辉县段渠道属深挖方段；渠道为梯形断面，坡比1∶2.25，底宽14 m，设计水深7 m，典型断面见图1；渠段设计流量260 m3/s，渠道比降1/28 000。2017年夏因暴雨造成地下水位偏高，排水不畅引起渗透压力大，致使某渠道边坡局部破坏，需要对边坡进行修复。

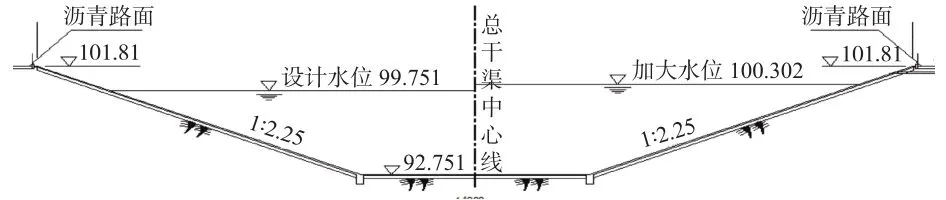
图1 渠道典型断面（单位：m）Fig.1 Typical cross section of the canal (unit: m)

钢围堰采用三面围堰，顺水流方向长97 m，横向范围达到左岸坡脚外3.7 m，钢围堰高7.5 m，满足最高水位的挡水需求。钢围堰上游是具有30°收缩角的迎流渐缩段，长32 m；中游是60 m长的顺流缩窄段，下游为长8 m的扩散段。图2为南水北调中线某渠段左岸渠道边坡修复开展生产性试验而设计的布置形式示意图。围堰面板由钢板和槽钢加工制作；以槽钢作为骨架，增加钢板的整体强度，同时迎水面钢围堰内侧需增设斜撑，抵抗水流冲击和局部壅水造成的压力。围堰底部与总干渠底板及渠坡设置橡胶或其他柔性垫层接触，于围挡底部设置预制混凝土块和砂石袋压重，顶部设置钢缆牵拉。钢围堰现场施工照片见图3，钢围挡的主要钢构件结构见图4。

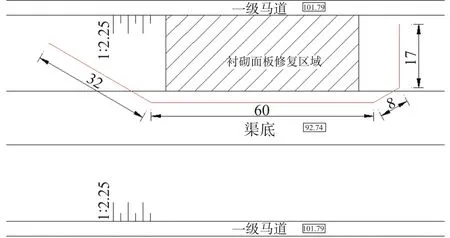
图2 钢围堰的平面布置及边坡修复生产性试验围堰区域（单位：m）Fig.2 Plane layout of steel cofferdam and production test cofferdam area for slope restoration (unit: m)

图3 钢围堰施工现场Fig.3 Construction site of steel cofferdam

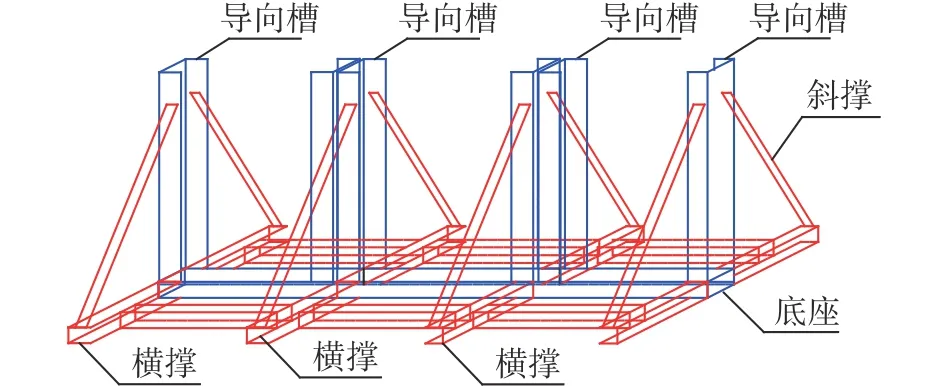
图4 渠底钢围堰导向架构造示意Fig.4 Structure diagram of steel cofferdam guide frame at the bottom of canal panel frame structure

现以原型观测数据为基础，选取两组不同工况的流量，通过已测水深及应力应变相关公式，对钢围堰的结构进行分析。钢围堰区域各特征断面的水深数据见表1。

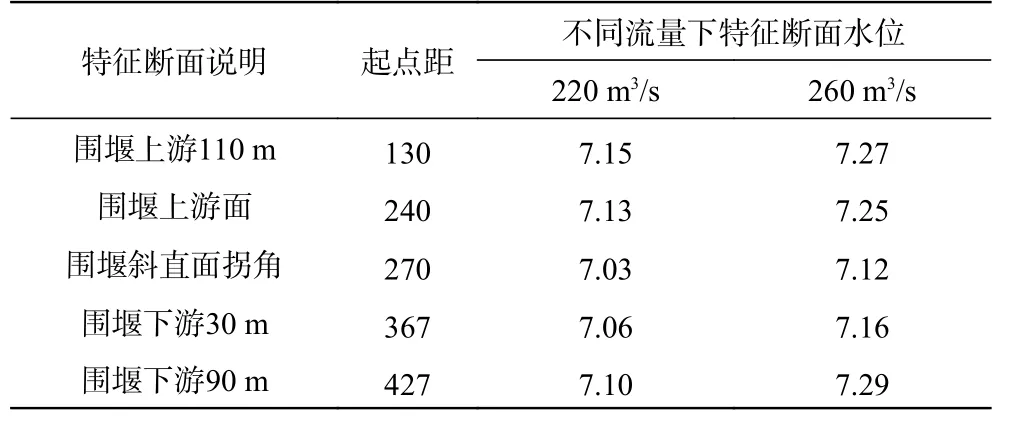
表1 不同流量下各特征断面水位Tab.1 Water level of each feature section under different flow conditions 单位：m

钢围堰各区长度：渠底围堰处的迎水面围堰长8 m，顺水流围堰长60 m，背水面围堰长8 m；渠坡围堰处的迎水面围堰长36 m，背水面围堰长18 m。渠底单体尺寸：围堰长6 m，高7.5 m，每个单体分3层，每层高2.5 m。单体结构说明：每个单体采用150 mm×100 mm×3 mm的矩形管、8#槽钢（支撑）、12#槽钢（导向槽）、Ф75 mm×3.75 mm的斜撑加工制作而成；其中矩形钢管与底部8#槽钢（纵横支撑）间采用焊接方式进行连接；导向槽与矩形管之间采用螺栓连接，斜撑与导向槽之间采用螺栓连接。单体之间通过M16螺栓连接固定。钢围堰挡板结构及尺寸：钢围堰挡板采用8#槽钢及3 mm厚钢板制作而成，8#槽钢与3 mm厚钢板之间焊接固定，单块钢挡板尺寸为2.50 m×1.95 m。模拟计算材料为钢材，密度为7 800 kg/m3，弹性模型为2×105MPa，泊松比为0.3，屈服强度为235 MPa，极限强度为375 MPa。

2 应力分析

水流在经过绕流物时，顺水流方向会对其产生拖曳力，垂直水流方向会产生压差阻力或动水冲击力。本次研究利用两种方法计算钢围堰所受水流冲击力。第1种采用动量原理，利用水流动量方程计算水流冲击力，计算式[7]如下：

第2种是采用流体力学中的绕流阻力计算方法，利用绕流阻力方程确定水流冲击力Fp，计算式如下：

式中：Cd为绕流阻力系数；Ad为垂直流向的绕流物投影面积；U为计算宽度内的垂线平均流速。

考虑到收缩段来流流速在横向分布的不均匀性，采用上述两种方法计算水流冲击力时，式（1）和（2）应表达成如下形式：

式中：FDi为钢围堰收缩段顺流向投影第i个分区所受绕流阻力。

经计算与综合分析，现状流量条件下，渠内动水压力作用在钢围堰上的压力荷载分别取500 N/m2和780 N/m2，下文记为工况1和工况2。

3 结构有限元分析

大型输水干渠外动内静水中作业钢围堰的结构分析属于流固耦合（FSI）系统的力学分析，其计算涉及复杂的流场边界条件和固体域的边界条件，为方便计算，本次研究将复杂流场边界条件简化为流体压力，并将其作用在结构上，进而分析钢围堰的力学性能。

3.1 模型建立

利用ANSYS Mechanical APDL的智能网格体积算法进行网格划分，钢围堰有限元模型如图5所示。参考张帅等[8-9]在单元技术上采用的方法，基于Timoshenko梁理论对钢围堰进行分析研究。模型中含有4 993个梁单元，214个杆单元，13 660个壳单元；共有18 867个单元，24 587个节点。坐标X轴指向左岸，Y轴指向与渠底垂直，Z轴指向水流方向。

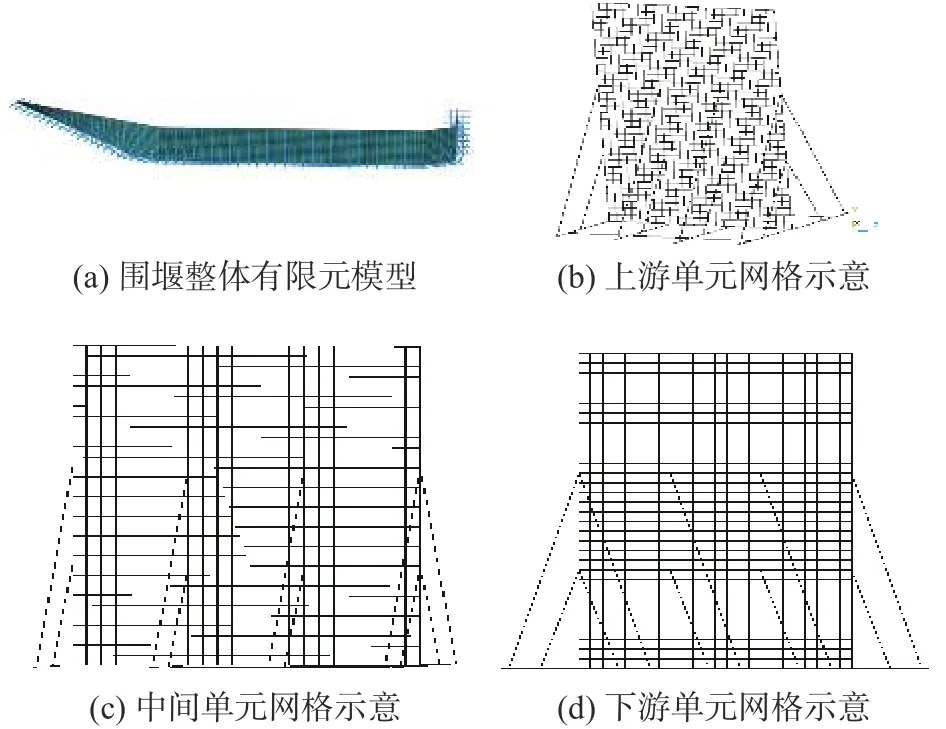
图5 围堰结构有限元模型Fig.5 Finite element model of cofferdam structure

（1）边界条件：渠道水深7 m，过流能力为265 m3/s，流速1.25 m/s，渠道横断面过流面积为211.8 m2。设置围挡后，围挡内面积为76.9 m2，剩余渠道过流面积为134.9 m2，考虑流速不变的情况下，渠道设计水位下的过流能力为168.6 m3/s。钢围堰上游最大正向落差为9 cm（外高内低），下游最大反向落差为-2 cm（外低内高）。

（2）荷载分布：本次研究荷载主要有水平荷载和竖直荷载。沿渠道顺水流方向的水平荷载包括水流对围堰的冲击力、围堰内外水位差产生的压力。竖直荷载为围堰自重荷载（水对围堰的浮力、摩擦力等可忽略不计）。

钢围堰材料为不锈钢，通常采用较为经典的Ramberg-Osgood模型[10]。本构关系的表达式为：

式中：E为材料的弹性模量；f0.2、f0.1为残余应变0.2%、0.1%时对应的应力；n为材料系数。

3.2 数值模拟

通过ANSYS数值模拟对钢围堰上、中、下游单元进行计算分析，在整体结果中，由应力场、变形量及轴力和弯矩来验算钢围堰的强度、刚度和稳定性。

3.2.1 强度分析 引入第二强度理论，无论是复杂应力状态还是简单应力状态，引起断裂破坏的主要原因都是最大伸长线应变[11]。因此，强度条件如下：

式中： σr2为第二强度； σ1、 σ2、 σ3分别为坐标轴X、Y、Z方向的主应力； [σ]为许用应力，由极限应力除以安全系数得到，安全系数取值为1.2～2.5；µ为泊松比。

对于上游单元，分别提取两组工况下对应的应力图，与钢围堰材料参数进行分析对比，进而判断上游单元的强度是否安全，见图6和7。

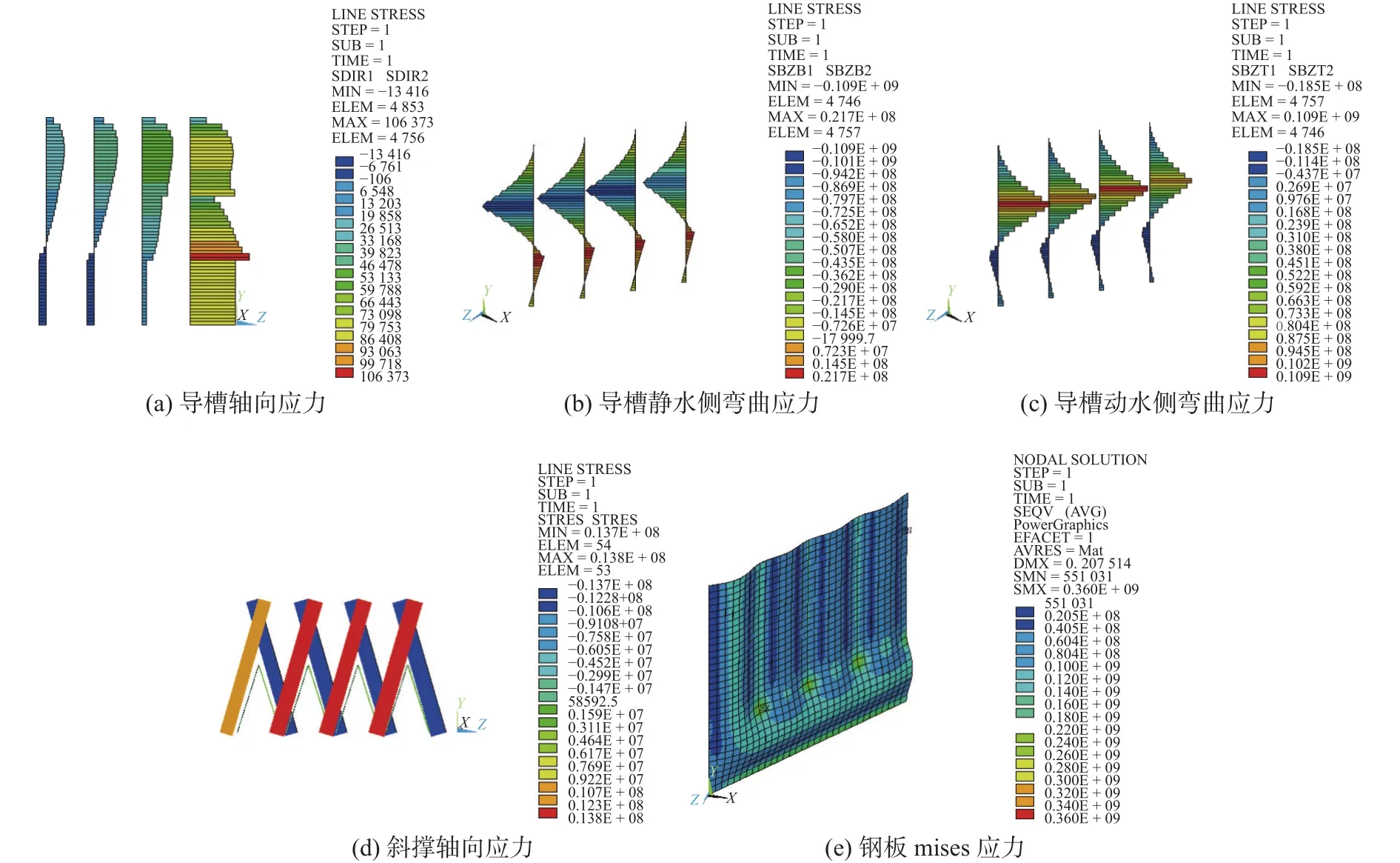
图6 工况1上游单元强度分析（单位: Pa）Fig.6 Strength analysis of upstream element of condition 1 (unit: Pa)

分析图6可知，导槽的轴向应力最大值为0.1 MPa，出现在该上游单元第4根导槽与短斜撑连接处；导槽的弯曲应力绝大部分为2.7 ～80.0 MPa，最大值为109.0 MPa，出现在导槽与长斜撑连接处；斜撑轴向应力最大值是13.8 MPa；面板应力最大值是360.0 MPa，出现在面板、导槽和短斜撑三者相连接的位置。

由图7可看出，导槽的轴向应力最大值为0.1 MPa，出现在该上游单元第4根导槽与短斜撑连接处；导槽的弯曲应力绝大部分为28.0～120.0 MPa，最大值为140.0 MPa，出现在导槽与长斜撑连接处；斜撑轴向应力最大值是17.7 MPa；面板应力最大值是356.0 MPa，在面板、导槽和短斜撑三者连接处。

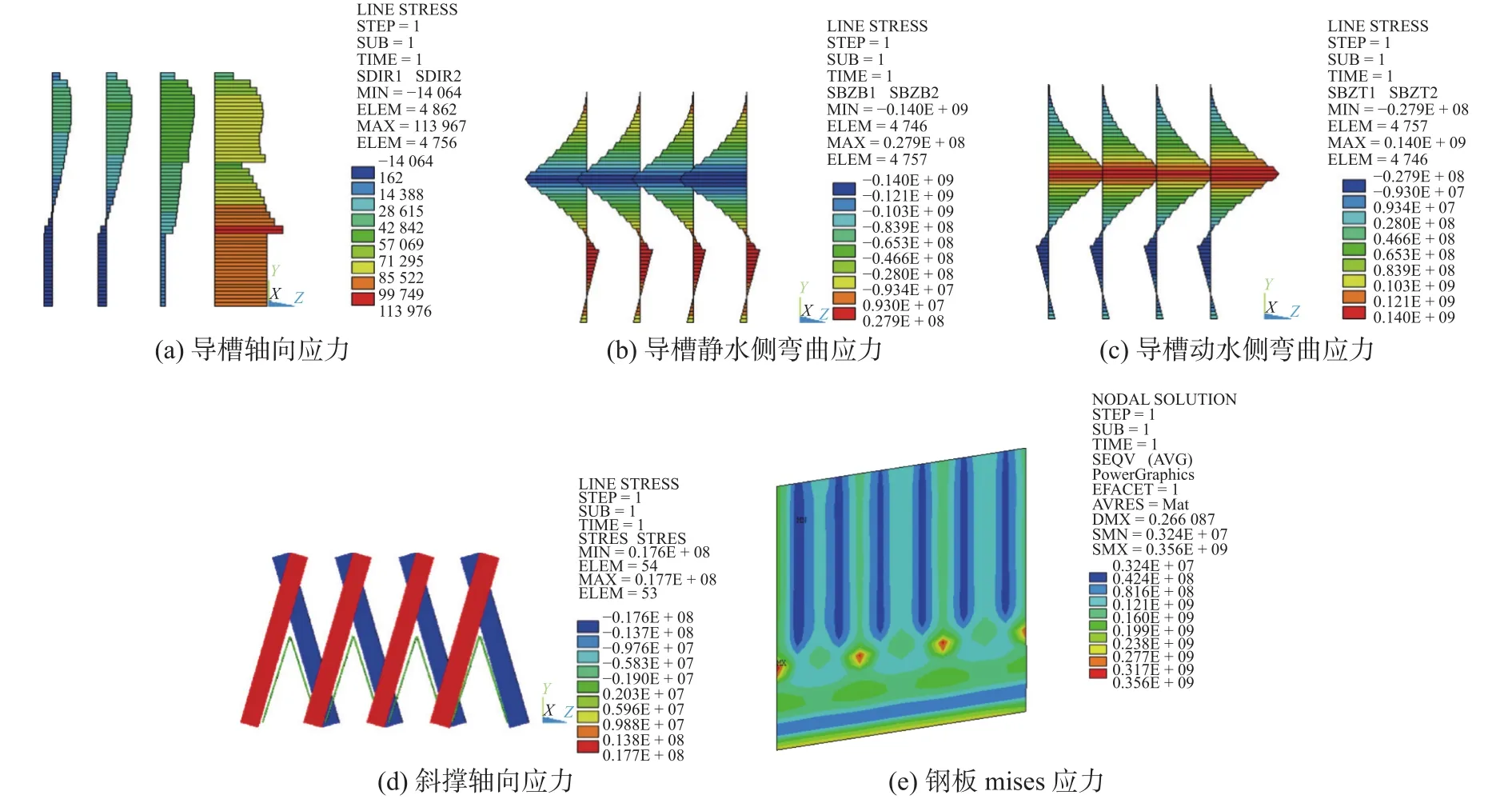
图7 工况2上游单元强度分析（单位: Pa）Fig.7 Strength analysis of upstream element of condition 2 (unit: Pa)

综上所述，在两组工况荷载作用下，钢围堰上游单元的应力都小于Q235a钢材的屈服强度，由第二强度理论可知，第二强度小于许用应力。因此，钢围堰上游单元强度是安全的。

同理，对于中间和下游单元，对强度的计算分析与上游单元相同。应力范围和应力最大值如表2所示。

表2 中间及下游单元应力Tab.2 Stress of middle and lower reaches element 单位：MPa

可见，两种工况条件下，各构件应力值均小于Q235a钢材的屈服强度，且第二强度小于许用应力，由强度理论可知，钢围堰中间和下游单元强度是安全的。

3.2.2 刚度分析 钢结构的整体刚度与钢结构构件的最大承载力和刚度密切相关[12]，根据钢结构设计标准的要求，导槽容许挠度值为18.8 mm，钢板的容许挠度值为37.5 mm。工况1和2中，上游单元刚度分析见图8和 9。

分析图8可见：工况1导槽的最大变形在导槽最上部，为39.0 mm，大于容许值；斜撑最大的变形在外部斜撑的最高处，变形量为0.7 mm；钢板的大部分变形量很小，约5.0 mm，但是结构下部板边的变形量却很大，变形量约为179.0 mm，大于容许值。

图8 工况1上游单元刚度分析（单位：m）Fig.8 Stiffness analysis of upstream element of condition 1 (unit: m)

分析图9可得：工况2导槽的最大变形也在导槽最上部，变形为50.0 mm，大于容许值；斜撑变形量为0.9 mm；钢板的大部分变形量很小，约为5.0 mm，但是结构下部的板边的变形量约为266.0 mm，大于容许值。

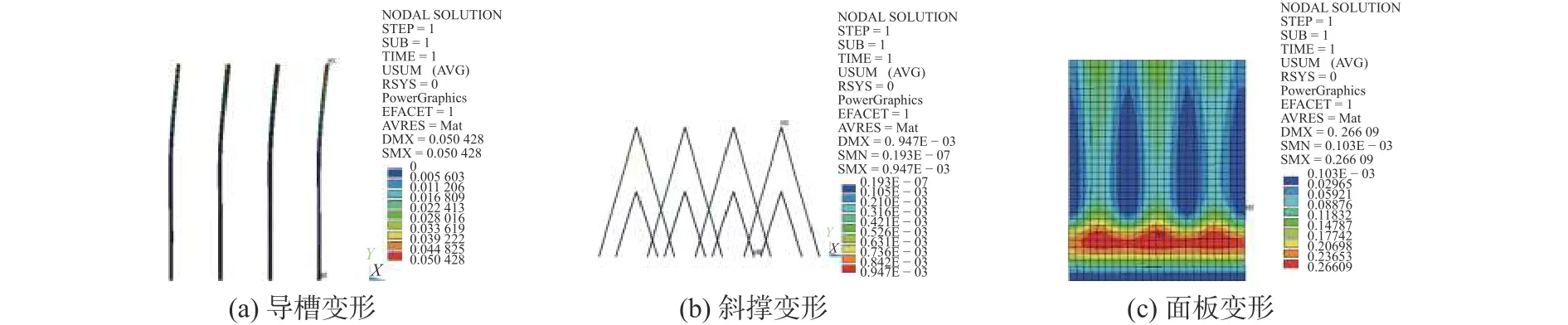
图9 工况2上游单元刚度分析（单位：m）Fig.9 Stiffness analysis of upstream element of condition 2 (unit: m)

对于中间和下游单元，单元变形量见表3。

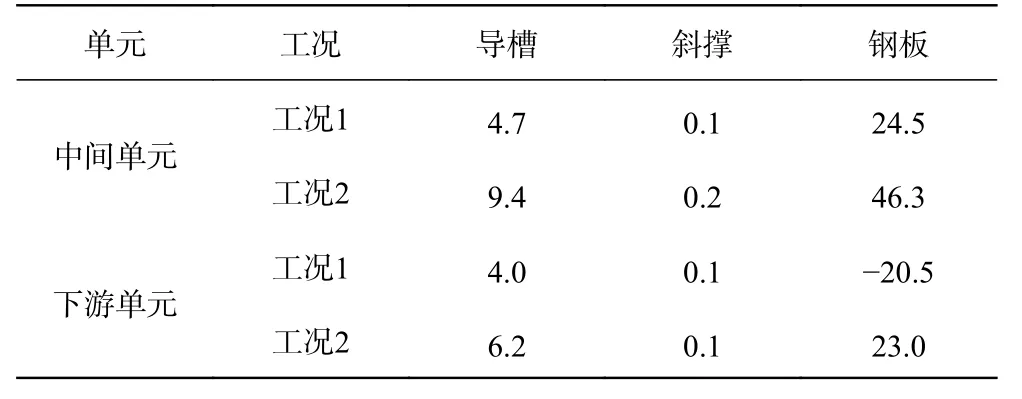
表3 中间下游单元变形量Tab.3 Deformation of middle and lower reaches’ element 单位：mm

通过对比分析可知，对于中间单元，在工况1条件下，导槽变形和钢板变形量均小于容许值；在工况2条件下，导槽的变形9.4 mm，小于容许值，但是钢板下边最大变形为46.3 mm，大于容许值。因此工况1条件下刚度符合要求，工况2钢板处有待改善。

对于下游单元，在2种工况条件下，导槽变形和钢板变形量均小于容许值，其刚度满足规范要求。

3.2.3 稳定性分析 钢围堰的稳定性分为导槽的压弯稳定和支撑杆件的轴压稳定。压弯稳定需要分析构件的弯矩和轴力，轴压稳定需要分析构件的轴力。弯矩作用在对称轴平面内的实腹式压弯构件，其稳定性按钢结构设计标准[13]（GB 50017—2017）校核。

平面内稳定计算式为：

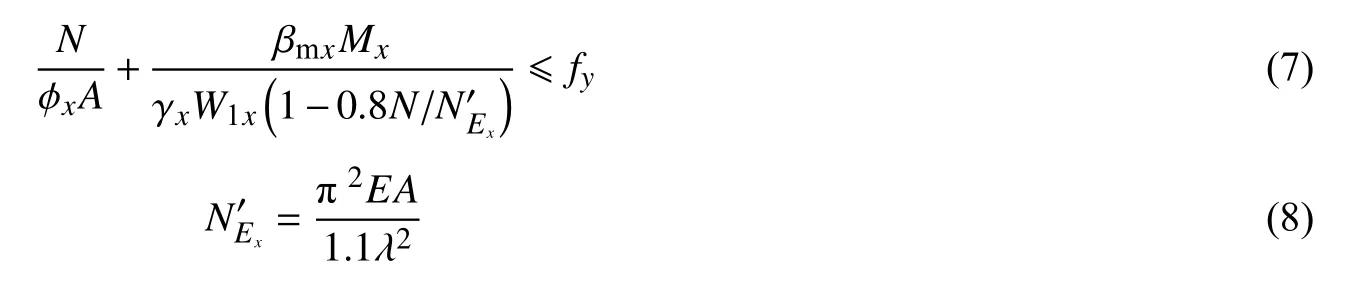
式中：N为所计算构件范围内轴心压力设计值（N）；为参数； ϕx为弯矩作用平面内轴心受压构件稳定系数；Mx为所计算构件段范围内的最大弯矩设计值（N·m）；W1x为在弯矩作用平面内对受压最大纤维的毛截面模量（mm3）；βmx为弯矩作用平面内的等效弯矩系数，在本构件中，全跨均布荷载：

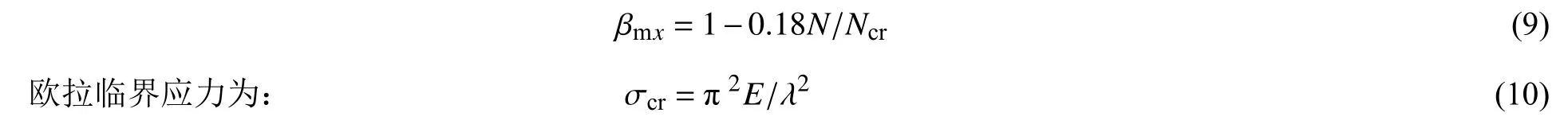
式中：Ncr为临界力；λ为长细比。

为研究围堰的稳定性，提取导槽弯矩、导槽轴向应力及斜撑杆轴力见图10。

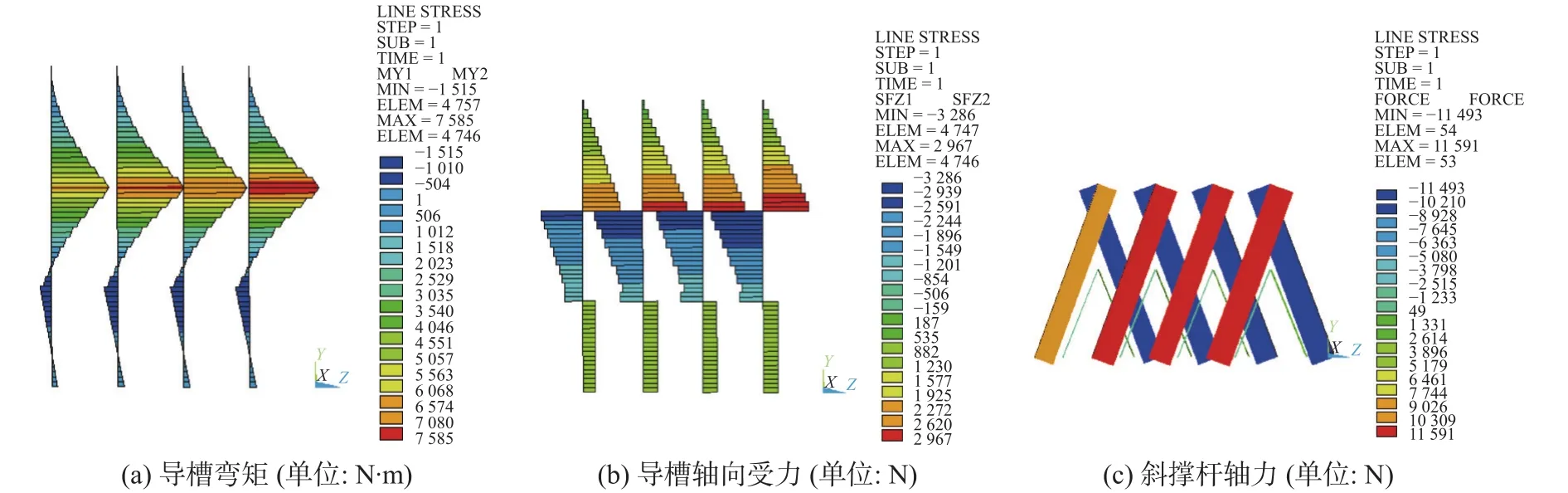
图10 上游单元稳定性分析（工况1）Fig.10 Stability analysis of upstream element (condition 1)

图10清晰体现了导槽在一定压力荷载条件下的受力状况。从上游单元整体分析看，由于第3部分处于水深最深处，水流流速相对较小，在有斜撑分担的情况下，其受到的轴向压力最小，为1 230.32 N。在上游来流量不变的情况下，动水压力荷载恒定，受轴向压力最大的是第4根（沿水流方向）导槽的第2部分，即中间一段，轴压力最大值为3 286.61 N，而其余3根所受轴压力差别不大。此时弯矩最大值为7 585.65 N·m，另外3根导槽的弯矩几乎无差别。总体上，4根导槽在斜撑的作用下，近似地被分成三部分，斜撑轴向作用力最大值为11 591.6 N。

分析图11可见，由于斜撑的作用，导槽近似被分为了3部分。其中受轴向压力最大的是第4根（沿水流方向）导槽的中间一段，轴压力最大值为4 228.1 N，而此时所对应的弯矩图中的弯矩最大值为9 760.8 N·m，斜撑轴向作用力最大值为14 903.3 N。

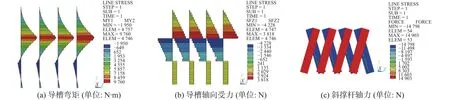
图11 上游单元稳定性分析（工况2）Fig.11 Stability analysis of upstream element (condition 2)

在第1种工况条件下，取构件长细比λ=46，欧拉荷载NEx=1 590 kN，抗力分项系数取1.1，由式（8）计算得：=1 445 kN， βmx=1，由《钢结构设计标准》附表D0.2按b类截面查表得稳定系数：ϕx= 0.856，由式（7）得出：fy=235 N/mm2＞2.234 N/mm2。对于斜撑杆件：该结构只受拉压的轴向作用力， λ =µl/i，该杆件两端铰接，μ=0.9，λ= 0.9 × 5 300/25.3=189，由钢结构设计标准可知，对于轴心受压构件，支撑的容许长细比为200，该结构为189，支撑杆件满足要求。由应力分析结果可知：支撑杆件轴向应力最大值为0.96×107Pa，由式(10)可以得出，欧拉临界应力为1.44×107Pa，考虑到实际杆件存在力学和几何缺陷，可以取修正系数0.7，得到修正后的临界应力为1.01×107Pa，仍大于支撑杆件轴向应力的最大值，支撑杆件稳定性基本上满足要求。

同理，对于工况 2，fy=235 N/mm2＞3 N/mm2，斜撑杆件轴向应力最大值为 1.77×107Pa＞1.44×107Pa，支撑杆件稳定性不满足要求。中间单元和下游单元的受力见表4。

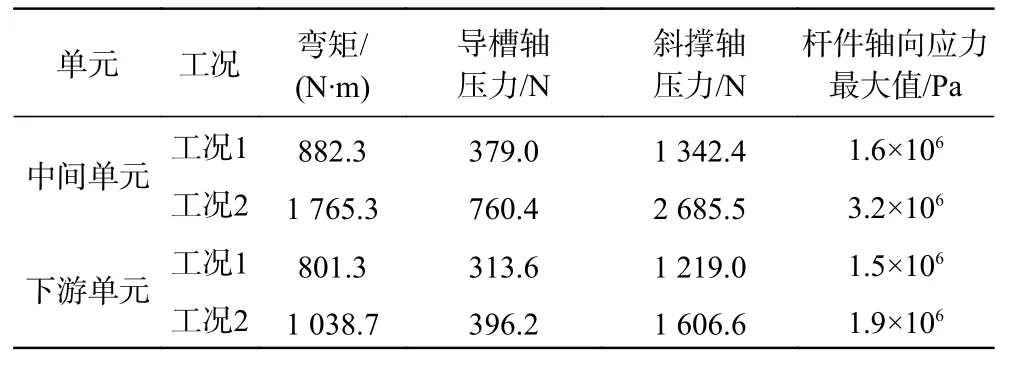
表4 中下游单元受力Tab.4 Force of middle and lower reaches’ element

对于中间单元第1种工况，由式（7）知：

因此，导槽稳定性满足要求。由表4可见，中间单元和下游单元稳定性均满足要求。

综上所述，钢围堰的导槽和支撑杆件都满足稳定性的要求，且稳定富余量较大，可以进行优化。

3.3 优化措施

由于下游单元导槽强度安全系数在2.0左右，建议将导槽12号槽钢（导向槽）调成10号槽钢，优化后的结构强度依然满足要求。针对钢围挡上游单元部分导槽构件挠度大于容许值的问题，可以采用焊接或螺栓连接，将各单元的槽钢两两相连，或采用工字钢锚固来加强结构刚度。针对上游单元支撑杆件刚度及稳定性不足，建议增大上游单元拐角处静水区斜撑，斜撑构件规格由Ф75 mm×3.75 mm调整增加为Ф75 mm×4.25 mm；为了减小导槽的变形，可以将斜撑上点支撑点向上移至1.25 m处来增强结构刚度。对于面板，部分工况上游单元和中游单元面板的变形量大于容许值，建议在钢面板静水侧水下部位增设竖向加劲肋，在水下将面板与导槽实施螺栓联结。

经计算分析，在两组工况条件下，优化后钢围堰的强度、刚度及稳定性均满足要求，可应用于实际工程。

4 结 语

建立了围堰结构的有限元模型，利用ANSYS数值模拟软件，对各构件的受力状况及整体结构特性进行了分析；对于典型的两组不同压力荷载，钢围堰整体强度符合要求。结构分析表明，在两组工况下，上游单元导槽和斜撑变形量较小，但面板变形量较大，钢围堰内部只有斜撑支撑，需要适当增加斜撑构件规格，将斜撑上的支撑点向上移来增强结构刚度。在钢板静水侧水下部位增设竖向加劲肋，改善结构受力条件。钢围堰上游单元部分导槽构件挠度大于容许值，提出了采用焊接或螺栓连接，将各单元的槽钢两两相连，或采用工字钢锚固来加强结构刚度的结构优化措施。在外侧动水条件作用下，钢围堰有向下游运动的趋势，需要在底部设置重物进行压重，以增大围堰与渠底的摩擦力。通过结构优化调整，提出了结构改进方法，成功应用于工程实际，为钢围堰的优化设计提供理论支撑。