海洋钻井隔水管系统动力学行为研究

2022-07-06朱志强冯颖韬温达洋山永林林黎明

钻采工艺 2022年3期

李旭，朱志强，冯颖韬，赵琥，温达洋，山永林，林黎明

1中海油田服务股份有限公司 2北京科技大学机械工程学院 3中国科学院力学研究所流固耦合系统力学重点实验室

0 引言

隔水管系统作为深水油气开采装备的重要组成部分，需要面对复杂海洋环境和气候条件的挑战。关于海洋隔水管动力学行为的理论研究最早始于1970年代，国外学者们通过Euler-Bernoulli梁的四阶微分方程来描述隔水管微元体的受力状态，建立了海洋隔水管的力学模型[1- 2]，也有学者将隔水管系统分成若干个部分，并通过一系列弹簧阻尼单元来连接模拟[3]。基于建立的力学模型，分析了隔水管轴向载荷和横向载荷的非线性耦合[4]，提出了一种考虑流体和结构不确定性的海洋结构响应统计特性评价方法[5]。国内学者们则对影响隔水管振动的各种因素进行了探讨[6]，建立了基于海洋环境和钻井工况耦合作用下的隔水管系统动力学控制方程[7- 8]，并基于隔水管力学性能实验，提出了深水钻井隔水管的“三分之一效应”[9]。还有部分学者分析了隔水管系统的固有频率[10]以及主共振的稳定性[11]，并利用接触单元模拟内外管接触的约束条件[12]。此外，Abaqus及其海洋环境模块Aqua被采用来对建立的隔水管-钻柱的管中管模型进行了动态响应分析，并将模型导入Isight优化软件，进行了基于可靠度分析的多目标优化设计[13]。

基于上述文献调研可知，对于海洋钻井隔水管系统动态响应的研究一直属于本领域的热点问题，而对于管柱系统这种连续体的振动问题，有限元分析又是最为有效的手段。然而，在已发表的论文中，关于隔水管系统动力学建模以及有限元分析的求解过程都未见详尽说明，容易引起困惑。因此，本文旨在详细介绍海洋钻井隔水管有限元建模及其求解流程，并进行隔水管单管的动力学行为研究。

1 海洋钻井隔水管系统的动力学建模

海洋钻井隔水管系统动力学建模是在所提出的基本假设的基础上，通过开展对隔水管系统动能、势能、外力做功三方面的数学描述，并最终基于Hamilton原理整合成为一个完整的动力学模型。

1.1 基本假设

(1)假设隔水管变形均在弹性范围内。

(2)假设隔水管是由均质、各向同性、线弹性的材料制成。

(3)假设隔水管变形和变形角是小量的，属于大应变小变形。

(4)暂不考虑钻柱对隔水管的碰撞影响。

1.2 隔水管系统动能

海洋钻井隔水管可以简化为弹性梁，其在海洋环境载荷的作用下将发生横向变形，从隔水管中取出一个单元体，其物理模型如图1。

图1 隔水管单元受力分析图

(1)

式中：mr—单位长度隔水管质量，kg;mf—单位长度的环空钻井液质量,kg;ϖ(x,t)—隔水管单元的横向偏移，m。

1.3 隔水管系统势能

势能包括应变能和任何保守外力的势能。根据应变应力关系得应变能为：

(2)

式中：E—隔水管的弹性模量,MPa。

另一方面，作为隔水管的内力，其轴向力是由隔水管的顶张力以及浮力共同决定的，可表示为：

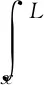
(3)

式中：Rtop—顶张力与隔水管与钻井液重量之和的比值，N/(m·kg);L—代表隔水管的总长，m;fb—代表浮力因子,无纲量;g—重力加速度，9.8 N/kg。

而当隔水管发生弯曲时，其轴向力将在横向上做功，当引入小应变大变形假设时，该轴向力做功可表示如下：

(4)

所以，总的势能可表示为：

V(x,t)=V1(x,t)+V2(x,t)

(5)

1.4 外力做功

在不考虑钻柱的情况下，隔水管所受的外力主要来源于海洋环境载荷，根据莫里森方程可知海洋环境载荷Ff(x,t)包括拖曳力FD(x,t)和惯性力FI(x,t)两部分，即：

Ff(x,t)=FD(x,t)+FI(x,t)

(6)

(7)

(8)

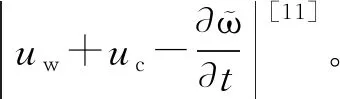
1.5 海洋钻井隔水管动力学模型整合

根据Hamilton原理的数学表达式：

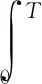
(9)

在一个海浪周期内，该隔水管系统的总能量可以描述为：

(10)

此外，隔水管系统的顶部通过转动刚度为Kt的挠性接头与平台连接，因此会随平台发生漂移；而隔水管系统底部则通过另一个挠性刚度为Kb的柔性接头固定在井口；因此，隔水管系统的顶、底处的初始条件和边界条件可分别表示为：

(11)

(12)

2 海洋钻井隔水管系统的有限元模型

首先，作为有限元分析的第一步，所建立的动力学模型需要被离散化。为了实现离散化模型的目的，采用弯曲梁单元的Hermite三次插值函数作为形函数，将包含形函数的位移近似解代入式(11)的动力学运动方程并化简得：

(13)

海洋隔水管系统的有限元模型表示为：

(15)

式中:[Mrm]—隔水管自身质量以及钻井液附加质量引起的质量矩阵；[MfI]—惯性力衍生的质量矩阵；[CfD]—拖曳力衍生的阻尼矩阵；[KEI]—弯曲应力引起的刚度矩阵；[KFa]—轴向力引起的刚度矩阵；[S]—位移列向量；[f]—外力列向量。

3 海洋钻井隔水管系统的动力学行为研究

采用Newmark积分法对建立的有限元模型进行求解，得到海洋钻井隔水管系统的动态响应。为研究钻井隔水管系统在海洋环境载荷作用下的动态响应，基于所建立的有限元模型，通过MATLAB编程对水深500 m的隔水管系统进行数值模拟研究。具体参数如表1所示。

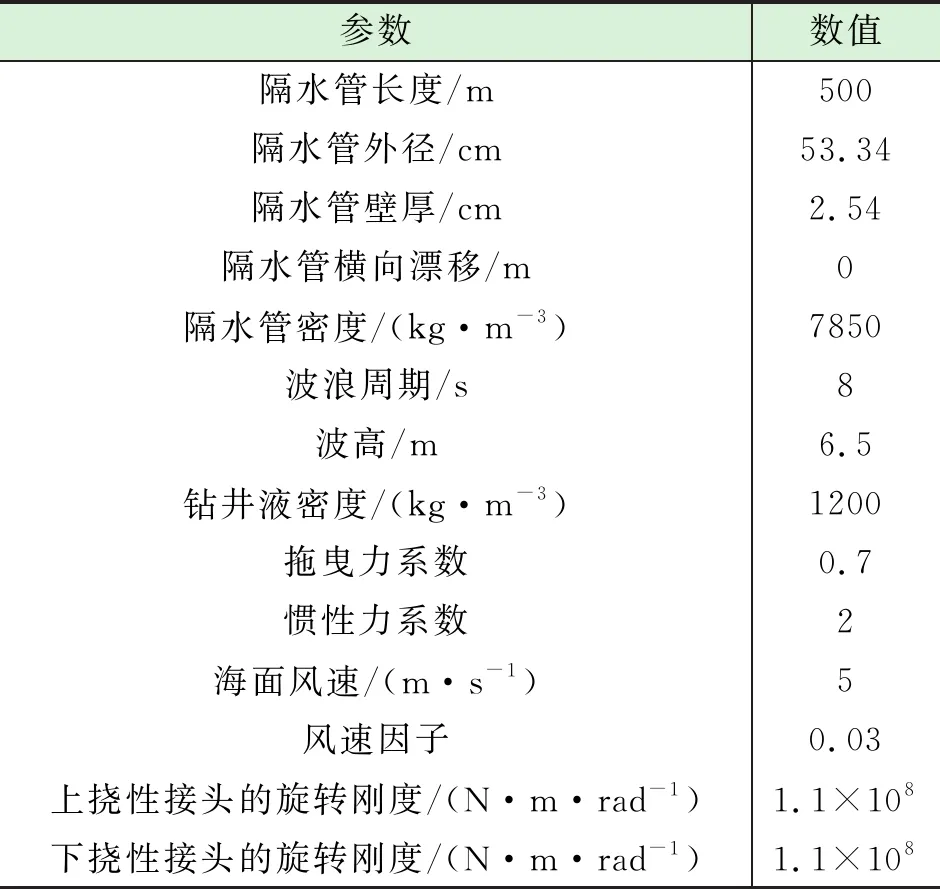
表1 隔水管具体参数表

对于一个水深为500 m的海域，海浪的影响主要集中于靠近海面的区域，且呈周期性变化；而海流的速度分布与时间无关，但会在海洋中上部摩擦深度所对应的位置发生一个突变[16]。

由于本文考虑的海洋环境载荷具有周期性，因而在其影响下的隔水管系统的动态响应最终也将达到动态稳定状态，而其判断标准是上、下挠性接头的转动均满足稳定的周期性特征。

随后，在确保隔水管系统的上、下挠性接头的转动达到其动态稳定状态下对隔水管壁厚、顶张力、浮力因子、海流流速、海浪波高等关键因素进行分析。

3.1 隔水管壁厚的影响

在实际应用中隔水管的标准壁厚大多为2.54 cm，因此分别选取标准壁厚、标准壁厚的2倍和3倍进行对比。从图2可以看出，隔水管壁厚对隔水管的动态响应有着显著影响。从左侧子图可以看出当隔水管壁厚增加时，隔水管的横向偏移和振动幅度都得到了有效抑制，从中间子图和右侧子图也可以发现随着壁厚的增加，弯曲应力和偏移挠度角都逐步减小。

图2 隔水管壁厚的影响

3.2 顶张力的影响

比较顶张力比分别为1.1、1.3和1.5的三种情况。从图3(a)子图和(c)子图可以明显看出，一旦施加较高的顶张力，隔水管的横向偏移和偏转角度都可以得到有效控制。但是犹如图3(b)所示，增大顶张力会导致弯曲应力增加，所以预设顶张力也不是越大越好。

图3 顶张力的影响

3.3 浮力因子的影响

浮力系数主要取决于隔水管外挂浮力块的设计策略。比较了浮力因子为0.5、0.7和0.9三种不同的方案。由图4可知，为降低对钻井平台的升力要求，在隔水管外部增加浮力块时，隔水管的横向偏移、弯曲应力以及偏移角度都明显增大。因此，为了有效控制隔水管的偏转，在钻井平台提升能力的允许范围内，建议选取浮力系数较小的浮力块设计策略。

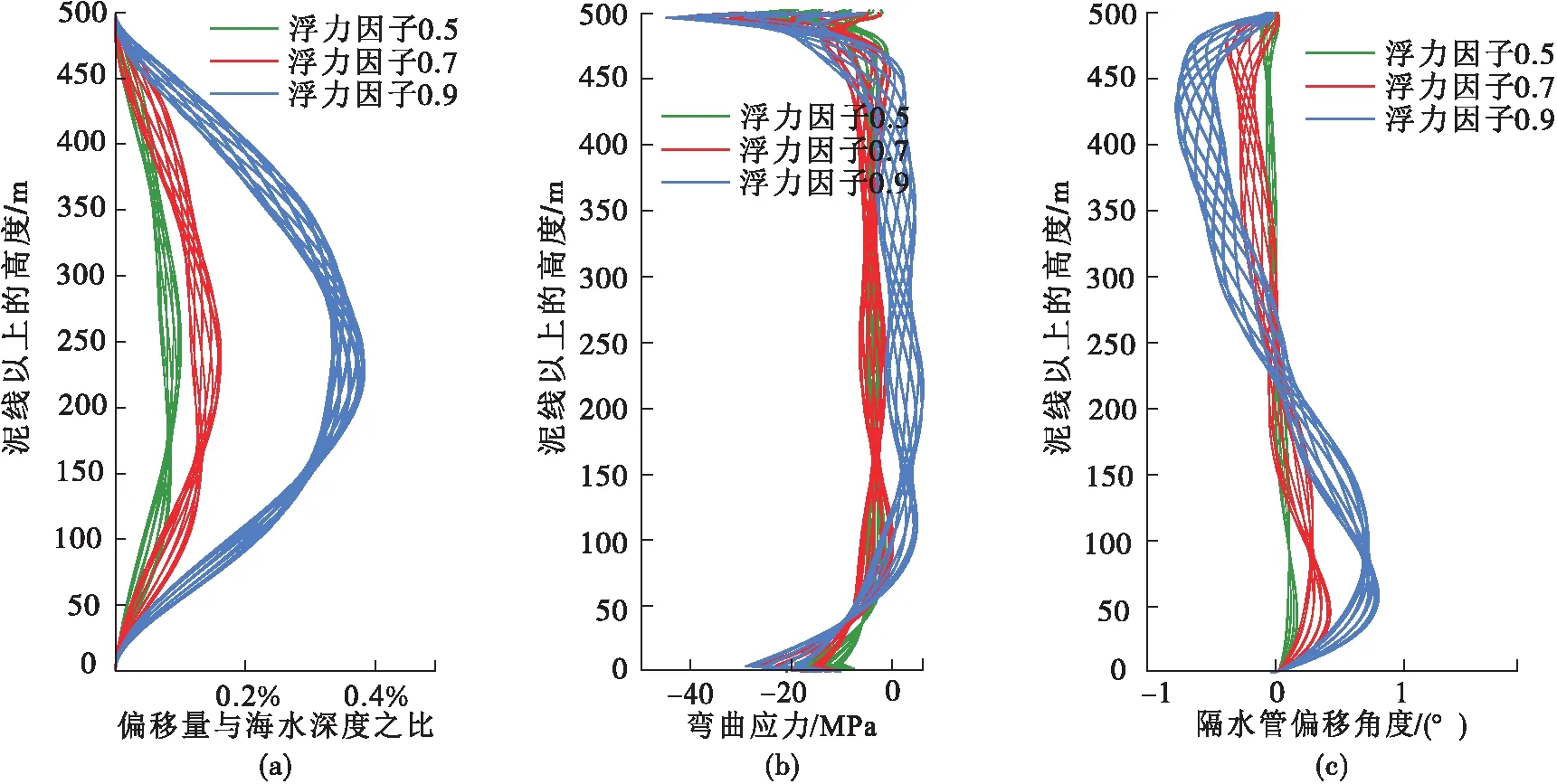
图4 浮力因子的影响

3.4 海洋环境载荷的影响

根据莫里森方程求解出海流水平运动速度Vc，分别比较0.5Vc，1.0Vc，1.5Vc三种不同海流速度下隔水管系统的动态响应情况，如图5所示。海流流速不仅影响隔水管顶部和底部的弯矩，对隔水管整体的振动也有着显著影响，虽然海流的速度会随着海深深度的增加逐步降低，但海流流速增加仍然会导致隔水管的横向偏移和偏转角度的增大。此外，海浪波高的增加对隔水管横向偏移的影响不明显，主要影响隔水管顶部，波高的增大将使得其弯曲应力和偏转角度增大，但海浪波高对隔水管动态响应的影响程度低于海流流速的影响。整体而言，为了保证隔水管的使用安全，针对不同的海洋环境进行隔水管系统设计时，要注意调整顶张力、浮力块配置等可控参数，来加强对隔水管系统横向偏移的抑制。