地层声波时差的Faust改进算法及应用
2022-07-06胡益涛程乐利
王 盼, 胡益涛, 刘 挺, 程乐利
1中法渤海地质服务有限公司 2长江大学录井技术与工程研究院
0 引言
声波时差法是随钻地层孔隙压力监测方法中较为准确及常用的方法[1],但笔者在现场实际地层压力监测工作中时常因随钻声波时差数据缺失而无法继续进行地层压力监测工作,其缺失情况主要为:目的层井段由于高温的限制或钻进过程中随钻工具损坏等无法继续使用声波时差测井工具,进而声波时差数据无法通过随钻工具正常测得;声波时差工具在安装时距离钻头的距离通常为20~30 m,现场应作业者要求须尽量将地层压力梯度计算至接近钻头深度以达到“深度实时”的目的,但钻头至声波时差测井工具之间的井段有20~30 m的井段声波时差数据无法测得。
目前根据国内外的研究成果,使用传统Faust经验公式对已钻井段缺失或无法测得的声波时差数据利用电阻率进行拟合[2- 4],经笔者在海上钻井现场实践发现:传统Faust经验公式拟合的结果虽然能反映声波时差的变化趋势,但不够精确,甚至在现场对地层孔隙压力解释中会影响工程师的判断,导致地层孔隙压力梯度评估出现偏差而无法为作业者调整钻井液比重提供有效的参考。为解决此问题,笔者对传统的Faust公式进行改进,并在中国南海西部东方、乐东、陵水以及永乐等区块18口高温高压井项目的实践过程中发现,改进后的Faust公式所拟合的声波时差数据精度多达95%以上,可满足现场的随钻压力监测以及完钻总结解释的基本需求。
1 Faust经验公式
1.1 Faust经验公式
Faust经验公式[5- 7]包含的变量为电阻率及垂深,即公式(1)所示:
vt=kHcdRD
(1)
式中:vt—声波速度,m/s;H—垂深,m;RD—电阻率,Ω·m;k、c、d—常数,具地区性。
声波时差由Δvt转换而得,即式(2)所示:
(2)
式中:Δt—声波时差,μs/m。
1.2 Faust经验公式在实际应用中存在的问题及分析
以L1井为例,沉积环境相同[2]井段972~2 669 m的全部数据点绘制成如图1a所示的趋势图;其中972~2 410 m的数据为的实测声波时差数据及电阻率数据,用来求回归函数,如图1b散点图所示;2 410~2 669 m的声波时差数据为回归分析Faust公式计算所得,如图1c散点图所示。
由图1可知,传统Faust公式拟合的声波时差数据变化趋势与实测声波时差数据整体上保持一致,相对误差为9.74%,决定系数r2为0.267 41,表明L1井的回归方程相关性较差。L1井钻进至2 410 m后随钻工具不能正常接收信号,钻到2 700 m后起钻更换同型号备用的声波时差测井工具,下钻对2 410~2 699 m未测声波时差的井段进行数据补测作业,补测结果与拟合结果平均相对误差达17.55%,尤其是2 500 m以后更为明显,整体偏小25~80 μs/m,导致现场利用声波时差法计算泥岩中的地层压力梯度偏小0.2 g/cm3以上,不能给作业者调整钻井液密度提供有效的参考。
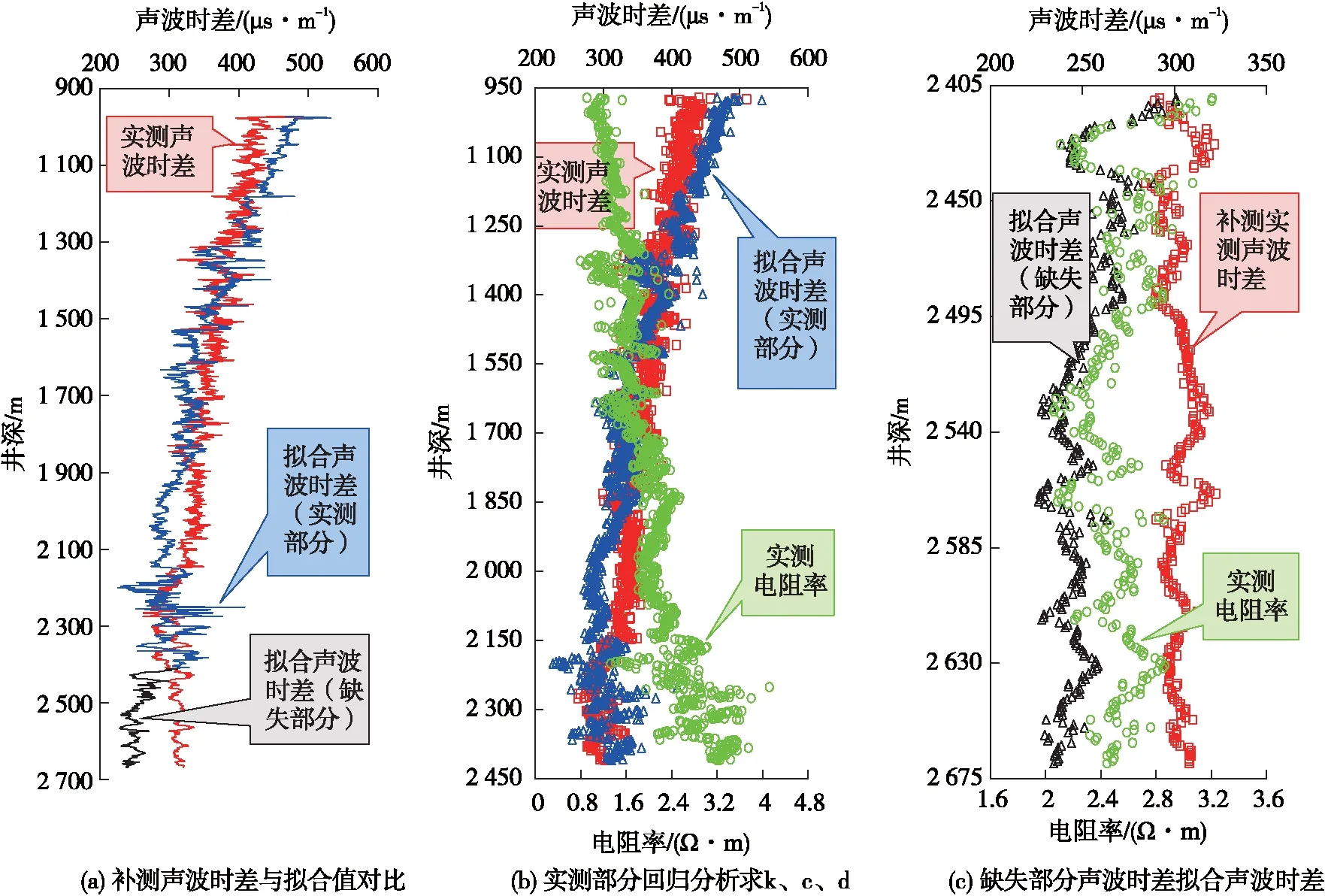
图1 L1井补测声波时差与传统Faust公式拟合声波时差对比图
为分析产生误差的原因,将过多口井或同一口井的不同井段的声波时差实测值与拟合值进行对比,部分对比图如图2所示。
通过南海西部多口高压井的随钻电阻率和拟合的声波时差对比,可发现两大特点:其一,如图2中D1、Y1、Y2井声波时差实测值与拟合值的对比所示,传统Faust经验公式受变量垂深H的制约,随着垂深H的增加,在大套泥岩井段浅部地层声波时差的拟合值比实测值大,深部地层声波时差的拟合值比实测值小,即拟合值整体上较实测值变化“速率”快。经分析Faust公式发现,此变化趋势为垂深H所致,垂深H作为拟合的变量之一,当k>0时,H与Δt呈正相关,则H与Δt呈负相关,此公式将导致:当电阻率变化幅度较小时,拟合的声波时差因为垂深H的增加依然呈现较为快速变小的趋势,与实测的声波时差变化趋势不一致。其二,如图2的Y2井所示,与D1井和Y1井对比可知当钻遇复杂岩性时,实测的随钻电阻率和随钻声波时差变化幅度较大,利用回归分析所得的Faust公式计算的声波时差变化幅度非常小,这与实测值因为岩性变化较大的趋势不相符,即拟合的声波时差数据精度较低。
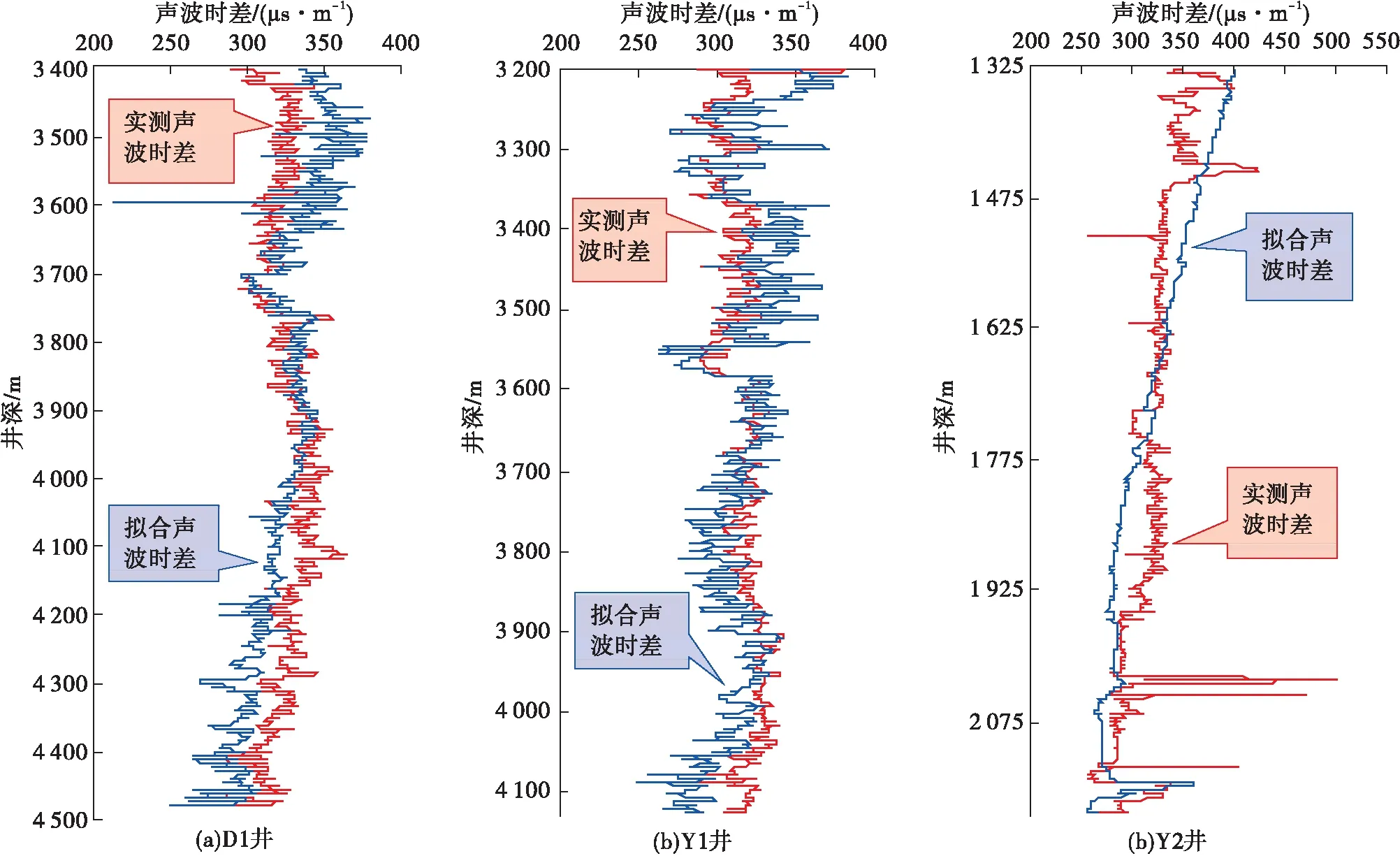
图2 多口井实测声波时差与传统Faust公式拟合声波时差对比图
2 Faust公式的改进
由上文分析的垂深H对拟合声波时差Δt计算的影响结合地层性质可知,电阻率RD与垂深H本身已经表现出一定规律:对正常沉积压实的地层,受压实作用、地温梯度、孔隙压力等因素的变化[8],较纯泥岩中的RD随着垂深H的增加呈规律性变大,即lnRD∝H。故笔者尝试着将Faust经验公式中的垂深H移除,并建立如下拟合模型:
(3)
式中:Δt—声波时差,μs/m;RD—电阻率,Ω·m;k、c、d—常数,具地区性。
改进Faust公式的拟合方法为:对式(3)变换后进行常规拟合,即对式(3)两边同时取自然对数[9- 10],并换元得:
(4)
由(4)式可得y=Ax+B,利用最小二乘法原理进行一元线性回归分析可求得A和B,然后反算出常数k、c、d即可。
在现场作业过程中,并非所有改进后Faust公式均可直接使用,可利用回归分析结果中的决定系数r2判断拟合回归函数是否符合预期[11],r2越接近于1,表明RD与Δt的相关性越强,r2计算式如下:
(5)
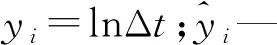
经南海西部东方、乐东、陵水以及永乐等高温高压或深水区块近18口井作业实践结果表明:当拟合报告中的决定系数r2小于0.7,或拟合得到的声波时差结果与实测声波时差相对误差大于5%,现场实际应用中相应计算的地层压力系数与MDT实测压力系数符合率普遍低于90%,无法为现场作业者实时决策提供有效参考,故在决定系数r2大于0.7时,声波时差拟合结果与实测值的相对误差在5%以内,作业现场的工程师可以考虑使用拟合公式来对缺失的声波时差数据进行拟合。
3 改进Faust公式的现场应用
3.1 试验井基本情况
2017年10月在中国南海西部乐东区块由中石化海上某钻井平台钻探的L2井为一口预探直井,设计井深为4 232 m,钻前地震预测目的层地层压力系数高达2.20 g/cm3,目的层作业窗口窄,将其归为一类风险井,设计井身结构为五开次,压力过渡带位于三开与四开,井眼尺寸分别为Ø444.5 mm和Ø311.2 mm,目的层位于四开和五开,井眼尺寸为Ø212.73 mm,详细井身结构数据如表1所示。目的层地层温度高达193 ℃,基于国内小尺寸井眼耐高温高压随钻声波工具的短缺及节约成本的考虑,设计目的层无随钻声波时差数据。
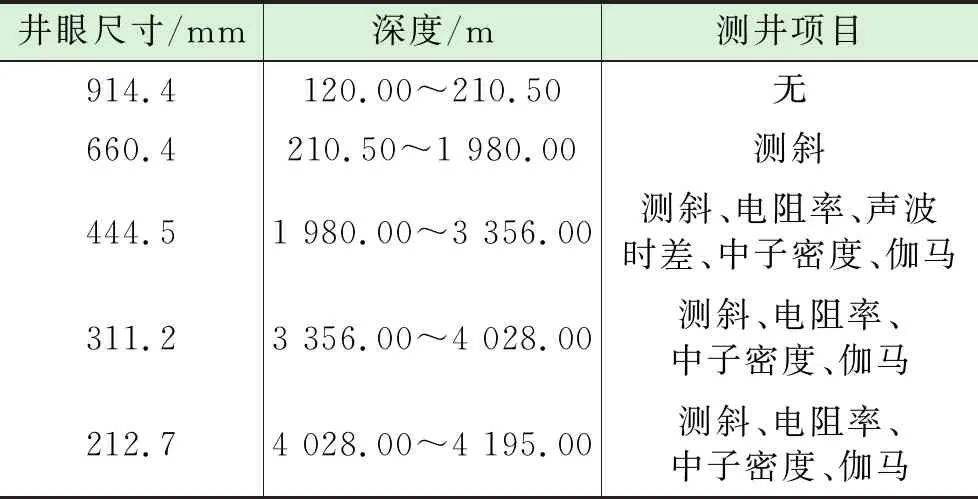
表1 L2井井身结构及随钻测井项目数据表
3.2 试验井测试过程
在实际应用中,使用改进Faust公式来对无法直接实测声波时差数据井段进行声波时差的拟合,并用拟合的声波时差来对地层孔隙压力梯度进行计算,结合井况对地层压力梯度进行综合评价。
由于地层压力过渡带压力梯度增长速率快,要求使用拟合声波时差数据来进行数据分析,为将声波时差数据实时更新至接近钻头深度,使用改进后的Faust公式对声波时差数据进行拟合,并根据拟合的声波时差数据对地层压力梯度进行初步计算。
将L2井三开井段垂深1 980~3 356 m的实测随钻电阻率数据及随钻声波时差数据利用(4)式进行回归分析,得改进后Faust公式中的k值为215.334 04、c值为3.574 83、d值为0.495 89,即得公式(6),和传统Faust经验公式(7)的表达式。
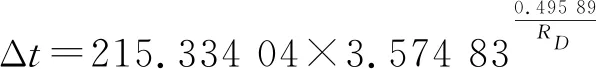
(6)
(7)
3.3 试验井测试成果
通过如图3随钻电阻率与各声波时差交绘图可以看出,改进Faust公式(图3a)对应决定系数r2为0.887 01,而传统Faust公式(图3b)对应的决定系数r2为0.610 66,通过上文可知,由于改进Faust公式对应决定系数r2更接近于1,因此改进Faust公式更符合预期并能满足现场作业需求。并利用式(6)和公式(7)分别对声波时差进行拟合,将拟合值及对应计算的地层压力梯度绘制成对比图如图4所示。
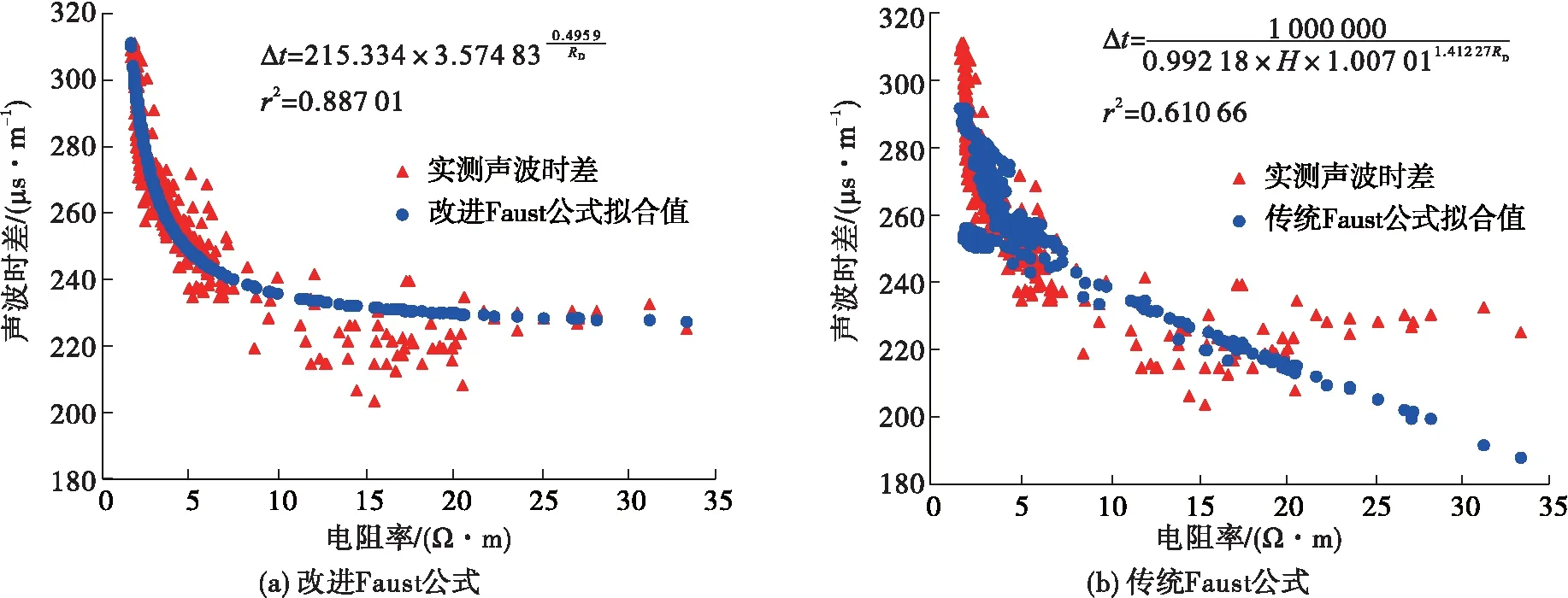
图3 随钻电阻率与各声波时差交绘图
由图4可知,改进Faust公式拟合的声波时差数据与实测值变化趋势一致,而传统Faust公式计算值随着井深的增加,相应计算的地层孔隙压力梯度在3 850 m以后开始出现偏差。在L2的实际钻探过程中,在录井时间气测曲线上可知钻进至3 987 m后每次接立柱后均会出现不同程度的单根气,且单根峰的幅度约为背景值的3~4倍,故可定性判断新钻开的地层压力梯度高于当时的钻井液密度,但图4中传统Faust公式计算值在3 910 m后与实测值偏差逐渐增加,相应计算的地层压力梯度偏小。通过表2可知:传统Faust公式拟合值计算的地层压力梯度符合率最低为58%,改进后的Faust公式拟合的声波时差计算的地层压力梯度符合率整体为96%~100%,故改进Faust公式拟合值更符合实际情况。现场的随钻地层压力监测工程师将两种方法的计算结果均给作业者进行了汇报,并在分析过程中强调了新Faust公式计算结果的可靠性,现场作业者迅速要求钻井液工程师对钻井液密度和性能进行了调整,有效地预防了溢流、井涌等复杂情况的发生。
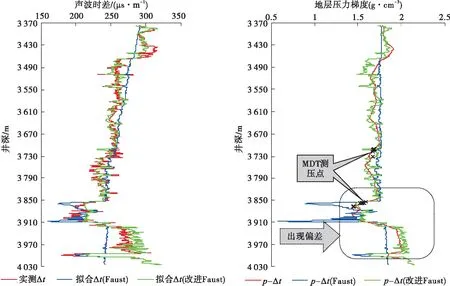
注:实测Δt—实测声波时差,μs/m;拟合Δt(Faust)—传统Faust公式拟合的声波时差,μs/m;拟合Δt(改进Faust)—改进Faust公式拟合的声波时差,μs/m;p-Δt-实测声波时差计算的地层压力梯度,g/cm3;p-Δt(Faust)—传统Faust公式拟合声波时差计算的地层压力梯度,g/cm3;p-Δt(改进Faust)—改进Faust公式拟合声波时差计算的地层压力梯度,g/cm3。

表2 L2井MDT测压结果与拟合声波时差计算结果对比
4 结论
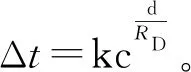
(2)改进Faust拟合函数计算的声波时差与实测值的平均相对误差为1%~5%之间,可满足现场作业需求。
(3)本文提出的新Faust公式经过实践可应用于随钻声波时差数据的拟合补全,亦可以应用于完钻后无电缆声波时差数据时的拟合,为钻后油气解释等领域也可提供必要的参考。
