基于字典序乘积下广义和连通度指标的上下界

李志豪， 朱 焱

（ 华东理工大学数学学院，上海 200237）

拓扑指标是与图的化学结构相关联的一种数学方法，分子图的拓扑指标值不仅可以定量地表达分子的结构，也能用来分析分子的结构与活性之间的关系，并且这些拓扑指标值在图的自同构下是不变的，所以它已成功地与有机分子的物理和化学性质相关联，因此对于拓扑指标的研究至关重要。但研究难点在于有些化合物分子比较复杂，拓扑指标的计算量比较大。

Onagh[6]研究了关于字典序乘积图的F-和的调和指标。Akhter 等[7]研究了关于笛卡尔乘积图的F-和的广义和连通度指标。Du等[8]研究了当非零实数大于或等于−1时，具有n个顶点的单圈图的广义和连通度指标的最小值和次最小值，并且确定了相对应的极图。Tomescua 等[9]确定了不同树的广义和连通度指标的最小值。

本文把基于笛卡尔乘积下运算图的广义和连通度指标上下界推广到基于字典序乘积下运算图的广义和连通度指标的上下界，然后计算了基于字典序乘积下运算图的广义和连通度指标的上下界，并对于每一个定理都分别给出了一个运算图的例子，计算了其广义和连通度指标，同时与定理中的上下界进行比较，从而验证了定理。

1 基本概念

令G是一个有限、简单、连通的无向图，其点集和边集分别为V=V(G) ，E=E(G) 。对于任意顶点v∈V，dG(v)表示v的度。Pn表示有n个顶点的路。对于给定的连通图G，4种相关图[10]定义如下：

(1) 在图G的每条边上嵌入一个新的顶点，将新顶点与所对应边的两个端点连接，这样图G中的每条边就变成了长为2的路，由此得到的图记为S(G) 。

(2) 在图G的每条边外，都加一个与之相对应的新的顶点，然后再把每个新的顶点与其相对应边的两个端点连接，由此得到的图记为R(G) 。

(3) 在图G的每条边上嵌入一个新顶点，将新顶点与所对应边的两个端点连接，然后再把图G中相邻两条边所对应的新顶点连接起来，由此得到的图记为Q(G) 。

(4) 在图G的每条边外，都加一个与之相对应的新的顶点，再把每个新的顶点与其相对应边的两个端点连接，然后再把图G中相邻两条边所对应的新的顶点连接起来，由此得到的图记为T(G) 。

如果G为P6，则S(P6) ，R(P6) ，Q(P6) 和T(P6)分别如图1所示。

图1 F∈{S,R,Q,T} 时F(P6)的4种运算Fig. 1Fouroperations ofF(P6)atF∈{S,R,Q,T}

两个连通图G0和G1的字典序乘积G0[G1] 定义为：其点集为V(G0)×V(G1) ，其图中的两个点 (a1,b1)和 (a2,b2) 相邻当且仅当a1与a2在G0中相邻或者b1与b2在G1中相邻且a1=a2[11]。

Sarala等[12]在两个连通图G0和G1的字典序乘积的基础上介绍了图的4种新运算。

令F∈{S,R,Q,T} ，则G0和G1关于字典序乘积的F-和G0[G1]F定义为F(G0)[G1]−E∗，其中E∗={(a,b1)(a,b2)∈E(F(G0)[G1]):a∈V(F(G0))−V(G0)，b1b2∈E(G1)}。

若G0=G1=P3，则P3[P3]S，P3[P3]Q，P3[P3]R，P3[P3]T如图2所示。

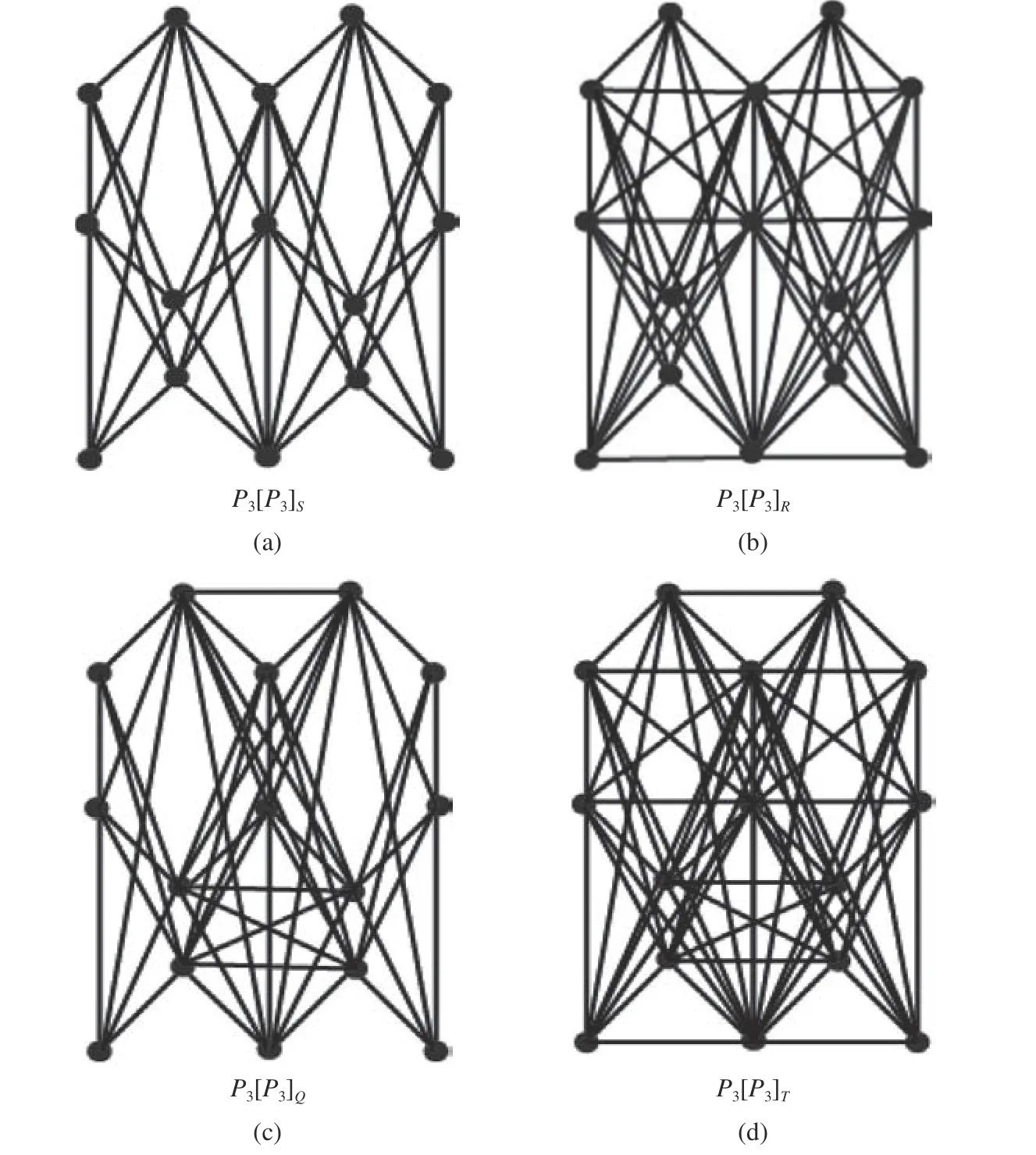
图2 F∈{S,R,Q,T} 时图P3[P3]的4种运算Fig. 2 Four operations on graph P3[P3] at F ϵ {S,R,Q,T}

2 主要结果

本文确定了关于字典序乘积图的F-和的广义和连通度指标的上下界。令n1,m1分别表示图G0的顶点数和边数，n2,m2分别表示G1的顶点数和边数， δG0和 ∆G0分别表示图G0的最小度和最大度， δG1和 ∆G1分别表示图G1的最小度和最大度。本文首先考虑F=S。

定理1当 α 为负数，广义和连通度指标满足不等式γ1(S)≤χα(G0[G1]S)≤γ2(S)，其中，

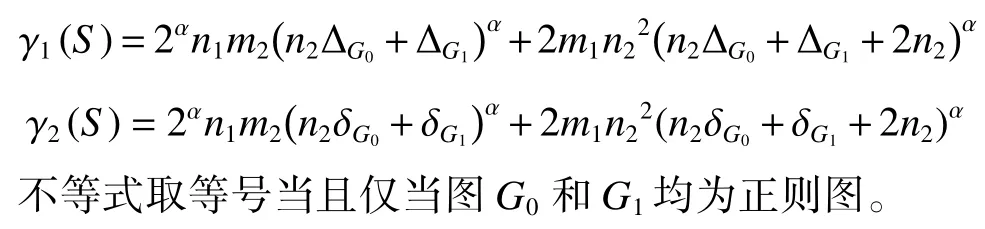
证明：

由于对于a1∈V(G0) ，有dS(G0)(a1)=dG0(a1) ，所以式（1）成立。

由等式 |E(S(G0))|=2|E(G0)|=2m1，当a2∈V(S(G0))−V(G0) 时，dS(G0)(a2)=2 ，所以

[n2dG0(a1)+dG1(b1)+2n2]α≥2m1n22(n2∆G0+∆G1+2n2)α

同理可得

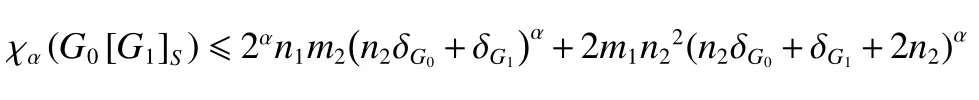
不等式取等号当且仅当图G0和G1均为正则图。

为了验证定理1的上下界，本文举例1说明。

例1：当G0=P4,G1=P2时，

χα(G0[G1]S)=2×6α+2×10α+8×7α+16×9α

γ1(S)=4×10α+24×9α

γ2(S)=4×6α+24×7α

满足 γ1(S)≤χα(G0[G1]S)≤γ2(S) 。

定理2当F=R时，对于负数 α ，广义和连通度指标满足不等式 γ1(R)≤χα(G0[G1]R)≤γ2(R) ，其中

不等式取等号当且仅当图G0和G1均为正则图。

证明：

由于 δG0≤dG0(a)≤∆G0,δG1≤dG1(b)≤∆G1，不等式取等号当且仅当图G0和G1均为正则图，因此可以得到

由于对于a1∈V(G0) ，有dR(G0)(a1)=2dG0(a1) ，所以式（2）成立。

由于dR(G0)(a1)=2dG0(a1) 、a1a2∈E(R(G0)) 和a1,a2∈V(G0) 当且仅当a1a2∈E(G0) ，因此

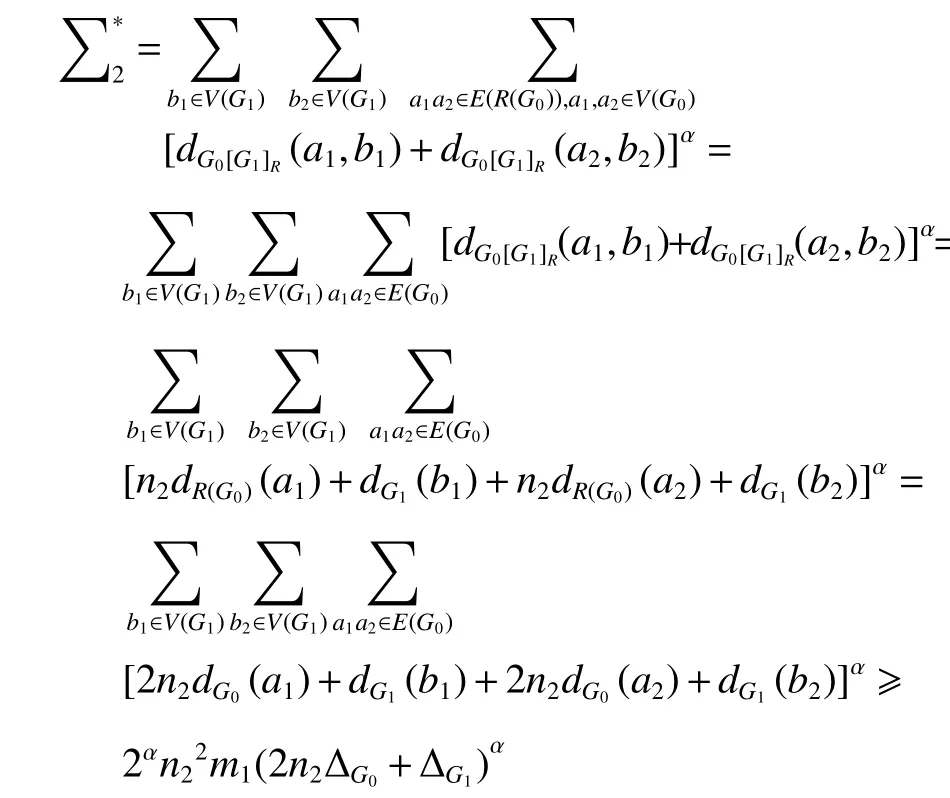
由等式 |E(R(G0))−E(G0)|=2|E(G0)|=2m1，当a1∈V(G0) 时，dR(G0)(a1)=2dG0(a1) ；当a2∈V(R(G0))−V(G0)时，dR(G0)(a2)=2 ，所以

不等式取等号当且仅当图G0和G1均为正则图。

为了验证定理2的上下界，本文举例2说明。

例2：当G=P4,H=P2时，

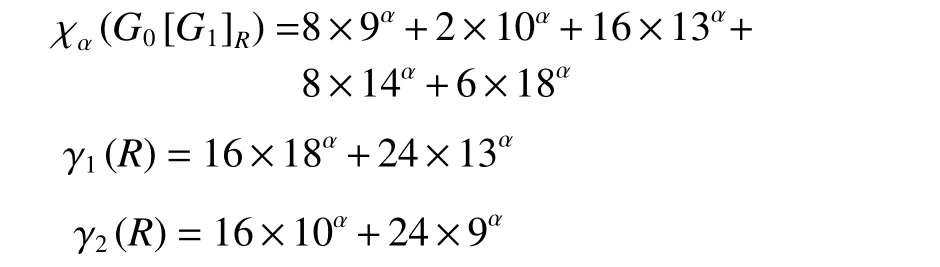
满足 γ1(R)≤χα(G0[G1]R)≤γ2(R) 。

定理3当F=Q时，对于负数α，广义和连通度指标满足不等式γ1(Q)≤χα(G0[G1]Q)≤γ2(Q)，其中

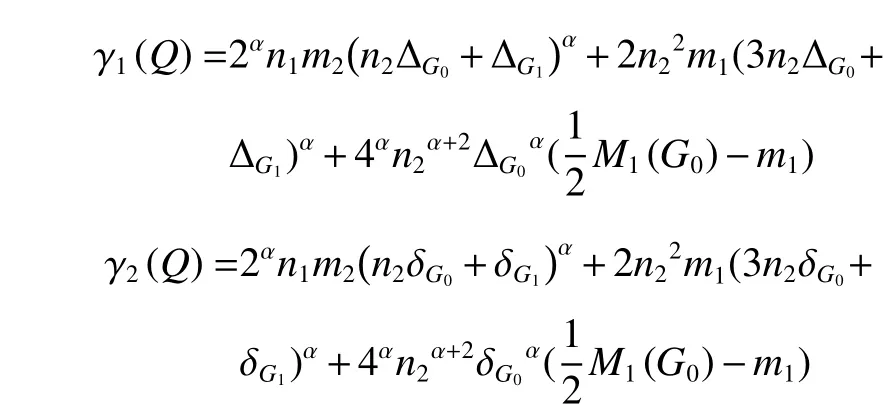
不等式取等号当且仅当图G0和G1均为正则图。

证明：

由于 δG0≤dG0(a)≤∆G0,δG1≤dG1(b)≤∆G1，不等式取等号当且仅当图G0和G1均为正则图，因此可得

由于对于a1∈V(G0) ，有dQ(G0)(a1)=dG0(a1) ，所以式（3）成立。

由于a1和a2分别对应于G0中的边wiwj和wjwk，因此

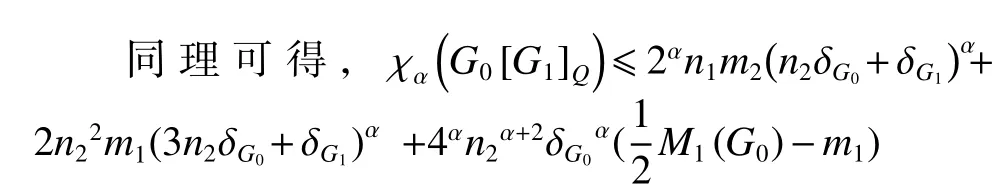
不等式取等号当且仅当图G0和G1均为正则图。

为了验证定理3的上下界，本文举例3说明。

例3： 当G=P4,H=P2时，

定理4当F=T时，对于负数 α ，广义和连通度指标满足不等式 γ1(T)≤χα(G0[G1]T)≤γ2(T) ，其中

不等式取等号当且仅当图G0和G1均为正则图。

为了验证定理4的上下界，本文举例4说明。

例4： 当G=P4,H=P2时，

χα(G0[G1]T)=2×10α+8×11α+16×14α+8×15α+8×17α+6×18α

γ1(T)=16×18α+8×16α+24×17α

γ2(T)=8×8α+24×9α+16×10α

满足 γ1(T)≤χα(G0[G1]T)≤γ2(T) 。

3 结 论

本文先给出了基于字典序乘积的4种运算，并得到运算图中顶点的度与未做运算的图的度之间的关系，再利用最大度和最小度计算了在 α＜0 的情况下基于字典序乘积的图的4种运算下的广义和连通度指标上下界，即 γ1(F)≤χα(G0[G1]F)≤γ2(F) ，其中F∈{S,R,Q,T}。如果α，>0那么γ2(F)≤χα(G0[G1]F)≤γ1(F)。因此对于其他的不同乘积，也可以把这4种运算推广到其他乘积上面，同样找出乘积图中顶点的度与图G0、G1中顶点的度之间的数量关系，再利用最大度最小度求出广义和连通度指标的上下界。不过困难的是对于有些乘积，很难找出乘积图中顶点的度与原图中顶点的度之间的关系。