双端动态事件触发下信息物理系统输出反馈H∞控制
2022-07-06王志文陈万杰孙洪涛
王志文,陈万杰,孙洪涛
(1.兰州理工大学 电气工程与信息工程学院,甘肃 兰州 730050;2.兰州理工大学 甘肃省工业过程先进控制重点实验室,甘肃 兰州 730050;3.兰州理工大学 电气与控制工程国家级实验教学示范中心,甘肃 兰州 730050;4.曲阜师范大学 工学院,山东 曲阜 273165)
计算技术、通信技术和控制技术的快速发展,引起了人类社会生活的巨大变革[1].基于这一背景需求,信息物理系统(cyber-physical system,CPS)应用而生,并迅速成为自动化领域的前沿研究方向,其相关研究工作已取得一定成果.随着信息物理系统的广泛应用,特别是在一些敏感领域的应用,例如:国防、核能、电网等,网络资源利用问题成为制约其发展的一个关键因素[2].
CPS通过共享的通信网络进行信息交换,但是信道带宽是有限的[3].在传统的CPS中,各个子系统都采用同步均匀的等间距进行采样,当确定了采样周期后,该系统所需要的网络带宽利用率也就相应的固定了,具有可预测性,且易于实现.20世纪90年代末,Karl等[5]首次提出了事件触发机制(event-triggered mechanism,ETM)的思想,之后事件触发控制引起了越来越多学者的关注.所谓事件触发控制,是指控制任务是否执行由事先给定的事件触发条件决定,而不是根据时间情况决定[4].与时间触发控制机制相比,事件触发控制方案可以减少计算资源、电池装置能源和通信资源使用[6-8].事实上,已经通过实验表明,事件触发控制方法可以有效地减少控制任务执行数量,从而在保证闭环系统性能的基础上,显著地节约通信资源[2].
近年来,人们对ETM的研究大多致力于设计事件触发条件,通过将设计的ETM 集成到控制回路中,开发了事件触发控制(ETC)系统.Peng等[9]提出一种双通道事件触发策略,实现网络化控制系统的异步事件触发.Zha等[10-11]在静态事件触发机制中引入动态变量,设计实现了动态事件触发策略(DETS),经过验证能够有效地增大事件触发间隔.Girard[12]通过设计双端动态事件触发策略,研究了网络化切换控制系统的动态输出反馈控制(DOFC)问题,但并未考虑系统存在的网络时延和系统扰动等外界因素.Aneel等[13]使用混合系统的方法,首次提出了一个非线性系统事件触发镇定的系统架构.Wang和Park等[14-15]分别研究了网络化控制系统的动态事件触发和动态输出反馈控制问题.Wang等[16]研究了一类具有随机耦合强度的时变网络的弹性滤波问题,引入事件触发策略调度传感器到滤波器的信号传输.Ge等[17]研究了网络化线性系统在拒绝服务攻击下基于观测器的事件触发控制问题.Wang等[18]提出自适应事件触发策略,针对一类具有未知执行器故障的非线性系统,设计了自适应容错控制器实现控制目标.在现有的文献中,对于ETC系统的研究主要集中在假设控制器和执行器位于同一位置的CPS,大多只考虑利用ETM节省传感器到控制器信道中的通信资源.然而,CPS的控制器和执行器位于不同的位置,这意味着设计传感器-控制器(S-C)信道和控制器-执行器(C-A)信道的事件触发机制显得尤为必要.
在现有研究成果中,还没有同时考虑含有双边时延和系统扰动的CPS动态事件触发和动态输出反馈控制问题的文献.基于此,上述问题激发了对本课题的研究,本文的贡献主要体现在以下三个方面:
1) 建立一个基于事件触发通信的具有两个区间时变延迟的线性系统,在统一框架下同时考虑通信和控制问题.
2) 在S-C信道和C-A信道引入DETS,建立具有双端时延和异步动态事件触发的控制系统.
3) 提出一种双端DETS和DOFC的协同设计方法,并证明了事件触发间隔的正下界,消除了Zone现象.
1 问题描述
CPS最基本的控制单元包括受控对象和控制器.考虑受控对象为如下线性时不变系统:
(1)
其中:x(t)∈Rn,u(t)∈Rp,y(t)∈Rq分别是系统的状态变量、控制输入和测量输出;z(t)∈Rz是系统被调输出;ω(t)∈l2[t0,∞)是系统扰动;A、B、C和Bω是适当维数的常数矩阵.
如图1所示,在S-C信道中,传感器以恒定采样周期采样设备的测量输出.ETM1确定是否应传输系统的采样输出,系统输出通过具有通信延迟的网络到达数据处理单元(DPU),DPU使用特定的时序将释放的设备输出传输到零阶保持器(ZOH),ZOH立即将释放的设备输出发送给DOFC.根据ZOH的性质,ZOH将保持系统被触发的输出信号,直到下一个触发量到来.
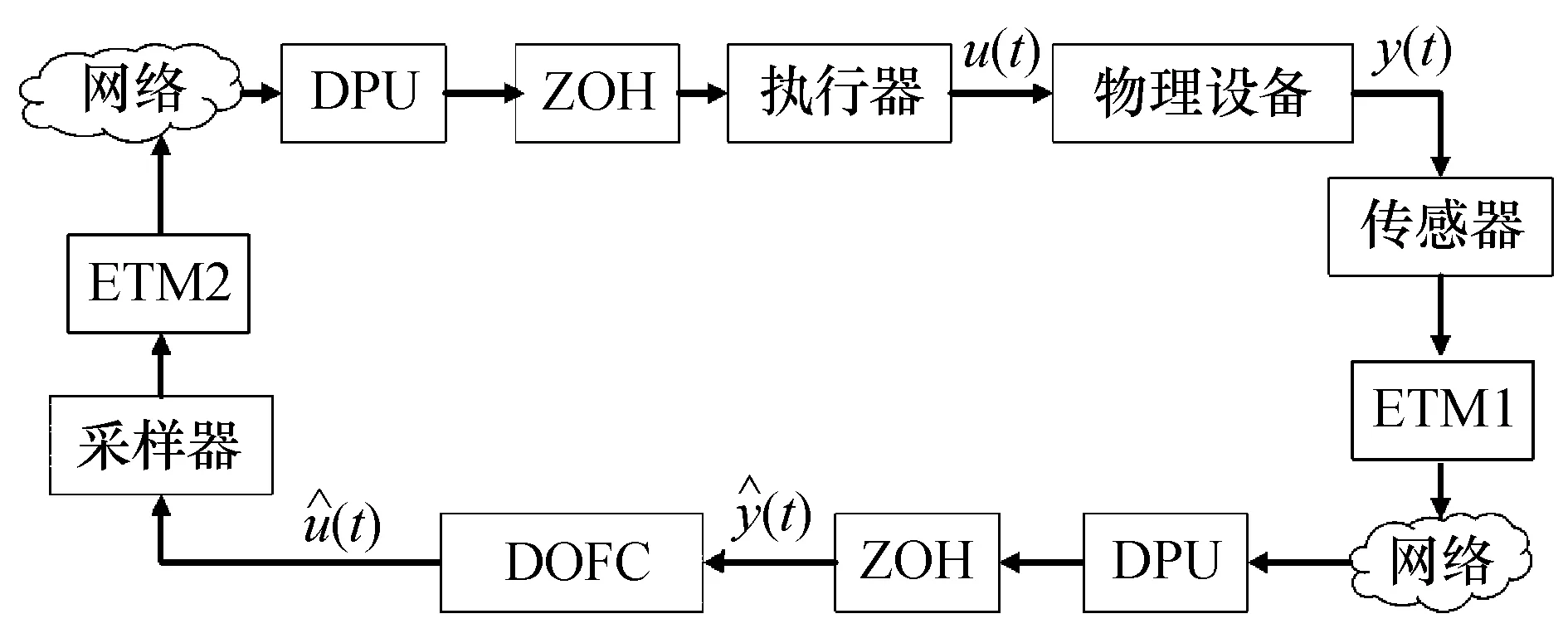
图1 CPS系统结构示意图Fig.1 Diagram of CPS system structure
定义测量输出误差和控制输入误差:
ey=y(bkh+jh)-y(bkh)
(2)
eu=u(dkh+jh)-u(dkh)
(3)
基于上述传输特性,S-C信道和C-A信道的下一触发时刻分别设计为
其中:y表示当前触发时刻的测量输出y(tkh);u表示当前触发时刻的控制输入u(tkh);β1,β2∈R;0<δ1<1,0<δ2<1是触发条件的自由度;定义动态事件触发条件的内部动态变量η1和η2为
其中λ∈R+.
对于S-C信道和C-A信道,η1和η2分别表示两个信道事件触发条件的灵活性.η1和η2越小,满足触发条件的可能性越大,则意味着触发次数会增加,触发时间间隔会减小.λ可被视为内部动态变量η的变化系数,λ越小,表示η的变化越缓慢.为得到更大的触发间隔,通常选择更小的λ值,确保η的变化率比误差的变化率小.η的取值大小决定η在事件触发条件中扮演的角色的重要程度.随着η值的增大,η对触发条件的影响将变小,同时意味着触发时间间隔变小.当η→+∞时,可将η对触发条件的影响忽略不计,此时动态事件触发变为静态事件触发策略(SETS).
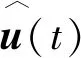
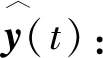
(8)
对系统的运行时间进行区间划分,定义
ρk=min{l|tk+lh≤tk+1,l=0,1,2,…}
(9)
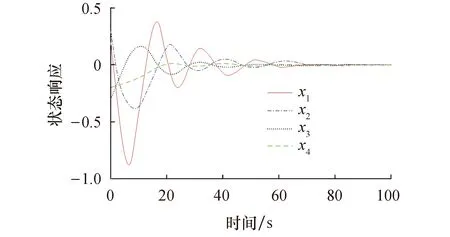
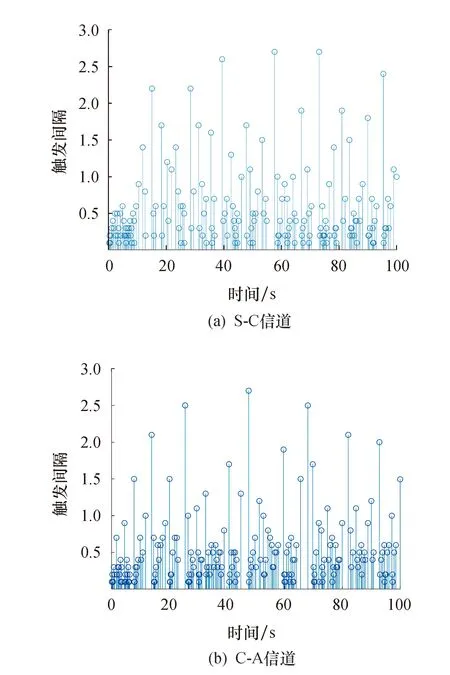
由tk (10) 控制器侧ZOH保持时间的划分与传感器侧类似,系统的全部运行时间表示为各个保持子区间的集合: (11) θ(t)=t-bkh-(ρk-1)h (12) 易知,θ(t)是一个分段线性函数,且满足: (13) 定义测量输出的误差函数ey(t)为 ey(t)=y(bkh)-y(bkh+(ρk-1)h)ey(t) (14) (15) 基于此,设计如下形式的动态输出反馈控制器: (16) 控制器侧DPU中的缓冲器接收并存储ETM2的最新传输数据,在每一时刻kh+τ(k∈N)如果缓冲区被更新,它的存储将被发送到ZOH.式(1)中的控制输入u(t)可以描述为 (17) (18) 同时,式(17)可被表示为 (19) 将式(19)带入式(1),并结合式(16),可得闭环系统模型: (20) 其中: (21) 引理2假设f1,f2,…,fn∶Rm|→R在Rm的开子集D中有正值,存在如下不等式: (22) 引理3对于矩阵和任意标量R≥0、X和任意标量σ,下面不等式成立: -XR-1X≤σ2R-2σ (23) 本节在闭环系统模型(18)的基础上,通过构造Lyapunov-Krasovskii函数(LKF)的方法,对闭环系统稳定性进行分析.设θ0=0,θ1=τ,θ2=(θ1+θ3)/2,θ3=h+τ,θ4=(θ2-θ1)/2,ξ(t)=col{ξ(t-θ1),ξ(t-θ2)},式(4)和式(5)的和η=η1+η2,则有 (24) 其中: 定理1对于给定的标量γ>0,在DETM条件(4,5)下,如果存在适当维数的实矩阵P>0,U>0,Q>0 (i=1,2,3),S1,S2时,且满足下列条件: (25) 系统(20)渐近稳定,且具有H∞性能指标γ. 证明构造一个LKF如下: (26) 取P≥0,U≥0,Q≥0,Rc≥0(c=1,2,3).其中: (27) (28) 可得η=η1+η2≥0,因此V(t)是正定的. 定义 χ(t)=col{ξ(t),ξ(t-θ1),ξ(t-θ(t)), ξ(t-θ2),ξ(t-θ3),ey(t),eu(t),ω(t)} 定义相关单位矩阵如下: 对V(t)进行求导: ζT(t)Qζ(t)-ζT(t-θ4)Qζ(t-θ4)= χT(t){[e2e4]Q[e2e4]T- [e4e5]Q[e4e5]T}χ(t) 由式(12,14,18)的定义可得: (29) 对动态事件触发条件的内部动态变量η(t)求导数: (30) χT(t){[e1-e2]R1[e1-e2]T}χ(t) χT(t){[e9(θ2-θ1)2R3e9T- χT(t){[e4-e5]R2[e4-e5]T}χ(t) [θ4-θ3]S3[θ3-θ5]T+ [θ4-θ3]R3[θ4-θ3]T- [θ3-θ5]R3[θ3-θ5]T}χ(t) 综合上述两种结论: γ2ωT(t)ω(t)+γ2ωT(t)ω(t) 其中: [e2e4]Q[e2e4]T- [e4e5]Q[e4e5]T+ [e1-e2]R1[e1-e2]T- (3-i)[e4-e5]R3[e4-e5]T- (3-i)[e2-e3]R2[e2-e3]T- (3-i)[e3-e4]R3[e3-e4]T+ (3-i)sym{[e3-e4]S2[e3-e4]T}- (i-2)[e2-e4]R2[e2-e4]T- (i-2)[e4-e3]R3[e4-e3]T- (i-2)[e3-e5]R3[e3-e5]T+ (i-2)sym{[e3-e5]S2[e3-e5]T}+ δ1[CE1e3+e6][CE1e3+e6]T+ δ2[CcE2e3+e7][CE1e3+e7]T+ [e6e7][e6e7]T 建立系统的H∞性能,构造函数J(t)如下: (31) 假设定理1成立,可得: (32) (33) δ1[CE1e3+e6][CE1e3+e6]T- δ2[CcE2e3+e7][CE1e3+e7]T+ Ψ21=col{Ω1,Ω2,θ1e9,(θ2-θ1)e9,(θ3-θ2)e9,Ω3} 将J(t)从t=[t0,+∞)积分: (34) 由于V(t0)=0,V(t)>0,所以可得 (35) 由上述结论,闭环系统满足H∞性能,证毕. 定理1中得到了闭环系统稳定的充分条件.然而,定理1中的控制器增益矩阵(Ac、Acd、Bc、Cc)都与未知矩阵变量P耦合,因此控制器的增益矩阵不能直接通过计算式(25)得到.基于此,定理2给出了控制器增益增益矩阵的一般形式,以便利用LMI 技术获得所需的控制器参数. (36) 则系统(20)渐近稳定,其具有性能指标H∞. 证明假设存在实矩阵P>0满足式(25),定义正定分块矩阵P如下: (37) 其中:Y、N、Y1∈Rn×n是正定矩阵;矩阵N是非奇异矩阵.设定Y1=NT(Y-X-1)N,由X>0,Y1>0和N是非奇异矩阵可知Y-X-1>0,对其使用Schur补定理,可得: (38) 分别定义矩阵J1和J2为 (39) 定义矩阵H1和H2,对定理1条件进行合同变换: 采用变量替换法,可得: (43) 其中: Φ6=[CXC],Φ7=[W10] 由式(43)可得,控制器增益矩阵可以表示为 (44) (45) 且控制器增益矩阵在式(45)中给出,证毕. 对于事件触发控制系统,事件触发器的最小事件触发间隔必须是正的,以避免Zeno现象.定理3给出动态事件触发的最小时间间隔. 定理3对于基于动态事件触发策略的闭环系统(18),动态事件触发机制(4)和(5)的最小时间间隔可以分别表示为τ1和τ2: 其中: a1=|λmaxA|,a2=|λmaxAc| δ1‖y(bkh)‖ δ2‖u(dkh)‖ b1=|λmaxA|‖y(bkh)‖+‖C‖‖B‖‖y(bkh)‖ b2=|λmaxAc|‖u(dkh)‖+‖Cc‖‖Bc‖‖u(dkh)‖ 证明与文献[14]中的证明过程类似,由于篇幅限制,此处省略该证明. 由0<δ1<1,0<δ2<1,可知式(46,47)中τ1>0,τ2>0,从而保证S-C信道和C-A信道的最小触发间隔是正的,进而消除了Zeno现象. 本节利用文献[19]中的卫星系统验证所提方法的有效性,其状态空间表达式为 其中:选择J1=J2=1,k=0.09,d=0.021 9.通过求解分析系统矩阵的特征值,可知开环卫星系统是不稳定的.假定卫星系统的初始状态x0=col[0.2,-0.3,0.3,-0.2],选择其他参数C1=[0 0 0 1],系统扰动ω(t)=0.1sin(2πt),γ=30. 根据定理2,利用Matlab的LMI工具箱求得系统的控制器增益矩阵如下: 系统的采样周期和时延分别为h=0.1 s和τ=10 ms,仿真时间为100 s.因此,在仿真时间内传感器共采集1 000个数据包.图2为双端DETM下闭环系统的状态轨迹,双端DETM下的卫星系统趋于稳定并实现了H∞控制性能. 图2 系统状态响应曲线Fig.2 System state response status 如表1所示,在式(4,5)中,分别选择动态事件触发传输自由度δ1=δ2=0.1,内部动态变量参数β1=β2=2.0,在S-C信道有183个数据包被成功发送,平均触发间隔为0.546 s;C-A信道有226个数据包被发送,平均触发间隔为0.443 s,其事件触发通信瞬间如图3所示. 表1 S-C信道和C-A信道的触发次数Tab.1 Trigger times of S-C channel and C-A channel 图3 动态事件触发通信间隔Fig.3 Dynamic event triggered communication interval 当β1=β2→+∞时,δ(t)对事件触发条件的影响可以忽略不计,DETM可以近似为SETM.图4为动态事件触发自由度δ1=δ2=0.1,事件触发内部动态变量参数β1=β2=99 999时的事件触发时间间隔.可以看出,相比静态事件触发策略,动态事件触发策略下能够传输更少的数据包,具有更大的传输间隔,在动态输出反馈控制系统中使用双边DETM能够保证满意的控制性能,可以有效节省S-C和C-A信道的带宽. 图4 静态事件触发通信间隔Fig.4 Static event triggered communication interval 为了定量说明该方法的有效性,选取不同的触发自由度δi和内部动态变量参数βi.事件触发条件下触发次数与各参数的关系见表2和表3. 表2 不同δi下的触发次数Tab.2 Trigger times under different δi 表3 不同βi下的触发次数Tab.3 Trigger times under different βi 针对传感器和控制器不在同一位置的CPS通信控制问题,构建基于双边动态事件触发策略的时滞系统模型框架.在提出的DETM下,动态输出反馈控制器能够保持系统稳定.通过引入一个内部动态变量来扩大事件触发间隔,减少数据传输次数,有效地降低S-C信道和C-A信道的通信负担.此外,还证明了双边动态事件触发的事件间隔存在一个正下界,避免了Zeno 行为.最后,通过卫星系统仿真实例说明了该方法的有效性.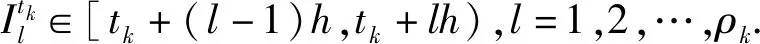
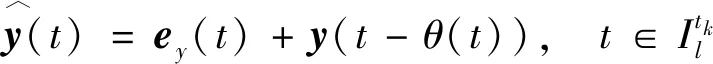
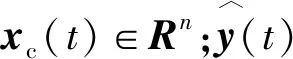
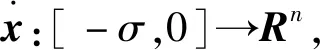
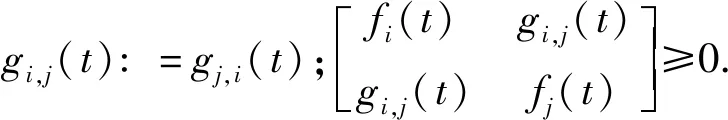
2 稳定性分析


3 控制器设计
3.1 动态输出反馈控制器设计
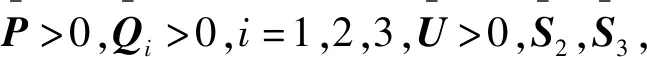

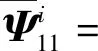
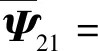
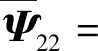
3.2 动态事件触发最小时间间隔
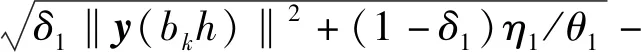
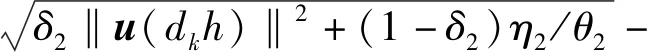
4 仿真算例




5 结论
