基于残差神经网络的滚动轴承故障诊断方法

朱奇先,梁浩鹏,赵小强,宋昭様

(1.大型电气传动系统与装备技术国家重点实验室,甘肃 天水 741000;2.兰州理工大学 计算机与通信学院,甘肃 兰州 730050;3.兰州理工大学 电气工程与信息工程学院,甘肃 兰州 730050)

滚动轴承作为旋转机械的核心部件，工作过程中起到支撑旋转体和降低摩擦系数的作用.由于滚动轴承工作条件复杂易变，会发生各种故障，可能导致意外事故和巨大的财产损失[1]，因此，对滚动轴承进行故障诊断是非常重要的.滚动轴承在实际工作中，在不同的载荷作用下和不同的噪声影响下，滚动轴承产生的故障对旋转机械的性能、稳定性和寿命都会产生巨大的影响，所以变工况条件下的滚动轴承故障诊断引起了学者们的广泛关注[2].为了能在不同的工作条件下保持轴承良好的性能，滚动轴承故障诊断方法需要在不同的负载和噪声条件下都具有良好的泛化和抗噪性能.有效的故障诊断方法不仅可以获得变工况条件下轴承的健康状态，而且能够对故障类型进行检测，这也是滚动轴承故障诊断中最具挑战性的任务[3].

目前，滚动轴承故障诊断的主要方法有信号处理方法和智能诊断方法，由于信号处理方法需要大量的专业领域知识和先验知识，这限制了它的应用.智能诊断是机械故障检测技术的新发展[4]，其中基于特征工程方法和基于人工神经网络(ANN)方法是两类常用的智能诊断方法.前者基于特征工程方法,主要通过特征提取和特征模式分类实现故障诊断.例如:袁莉芬等[5]利用小波包优先选的方法能有效地提取特征中的故障信息；Wang等[6]结合局部均值分解和快速峰值的优点处理故障特征，检测旋转机械的故障；唐贵基等[7]针对轴承早期故障特征微弱，难以提取等问题，提出了一种变模态分解(VMD)的方法；李宏坤等[8]提出了一种粒子滤波方法，解决了谱峭度指标在噪声干扰下效果较差的问题；Mao等[9]利用支持向量机(SVM)作为特征模式分类算法并与多尺度排列熵结合来诊断轴承的健康状况，并取得了良好的分类效果；陈鹏等[10]提出了一种VMD与多分类支持向量机(MRVM)相结合的方法，可有效地识别出不同位置的故障.虽然此类方法取得了一定的成果，但是在故障诊断的过程中仍需要人工提取特征向量，具有专业依赖强、特征提取困难等问题，限制了这类方法在故障诊断领域的发展.

近年来，随着深度学习的兴起，基于人工神经网络(ANN)的方法蓬勃发展[11]，例如：Zhang等[12]利用快速傅立叶变换(FFT)转换原始信号作为输入，通过一种第一层为宽卷积核的深度卷积神经网络(DCNN)，取得了不错的效果；Lu等[13]利用深度堆积去噪自编码器对轴承进行了全面的故障诊断.考虑到深度学习模型可以直接处理原始数据而无需任何数据预处理，已经有一些基于人工神经网络的滚动轴承故障诊断方法直接处理原始振动信号，例如：Jiang等[14]利用卷积神经网络来学习原始数据中时频数据的特征，并证明了采用该网络进行特征学习可以提供比手动特征提取更好的结果；孔子迁等[15]分别利用卷积神经网络提取轴承信号中的频域特征，双向门控单元提取轴承信号中的时域特征，最后采用注意力机制进行特征融合，解决振动信号中时频域特征信息难以充分挖掘的问题；陈志刚等[16]提出了一种集成深层自编码器(IEDAE)方法，能有效地对变工况条件下的滚动轴承故障信息进行自动提取与识别；Zhang等[17]进行了大量轴承故障诊断仿真实验，结果表明基于深度学习故障诊断方法的泛化能力优于传统特征提取方法.

以上基于人工神经网络的方法表现出较好的故障诊断能力，同时在故障诊断领域具有较好的发展前景.尽管此类方法具有避免由环境噪声和工作条件波动引起的虚假特征的巨大潜力，但它仍然需要巧妙的结构设计以避免轴承振动信号的错误特征.此外，由于滚动轴承工作环境的复杂性，需要故障诊断方法能够深度挖掘轴承信号中的特征信息，从而有效地实现变工况条件下的故障诊断.因此本文提出一种基于残差神经网络的故障诊断方法.该方法首先利用三个连续的卷积层串联构建了一种改进的数据池化层，增强特征提取能力并减少参数数据量的计算；然后结合空洞卷积和残差块构建空洞残差块，并在残差神经网络中加入该残差块扩大感受野，从而提升该方法的特征学习能力；最后引入Dropout方法丢弃一定比例的神经元，有效避免深度神经网络故障诊断因有效数据量少而产生的过拟合问题，取得了较好的滚动轴承诊断效果.

1 相关理论

1.1 残差神经网络

2016年He等[18]在卷积神经网络的基础上设计了残差神经网络(residual neural network,Resnet)，有效地解决了深层卷积神经网络的梯度消失问题，并在ImageNet图像识别比赛上大放异彩.残差神经网络引入了残差学习的概念，通过多个首尾相连的残差块来学习残差特征，残差块结构如图1所示.其中:x为残差神经网络的输入;H(x)为输出，F(x)为残差映射函数，H(x)=F(x,{Wi})+x为恒等映射函数;Weight layer为卷积层.残差神经网络在普通深度卷积网络的基础上增加跨层拟合训练残差，只学习输出和输入的差别，He等[18]通过实验证明，拟合残差映射函数F(x)=H(x)-x比去拟合一个恒等映射函数H(x)=x要容易的多，并且在训练过程中底层误差可以通过快捷连接传递给上一层，使得训练过程中除了使用目标函数梯度外，还增加了残差梯度，因此残差神经网络在具有较深层数的同时，也具有更强的特征学习能力.

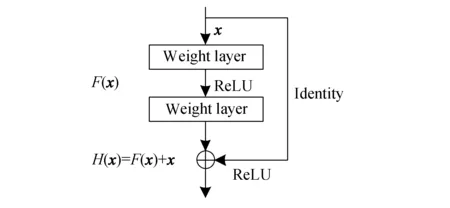
图1 残差块结构Fig.1 Structure of residual block

1.2 空洞卷积

空洞卷积是一种可以增加卷积层感受野的卷积方法,它的概念于2016年Yu等[19]提出.空洞卷积可以通过跳跃步长来获得数据特征，输出更多的信息并保持参数不变.假设x(a)代表特征输入，特征长度为A，r代表膨胀率，w(i)代表卷积核大小，y(a)代表空洞卷积运算后的输出特征.它们之间的关系式如下：

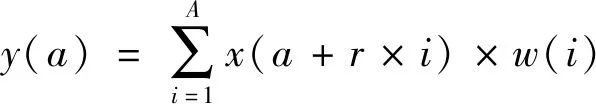
(1)

对于卷积核大小为K的普通卷积，在以r的空洞率执行空洞卷积运算后，卷积核的大小将等于K+(K-1)(r-1).例如，在空洞率为2的空洞卷积运算后，卷积核大小为3的普通卷积相当于大小为5的空洞卷积核，其中空洞卷积过程如图2所示.

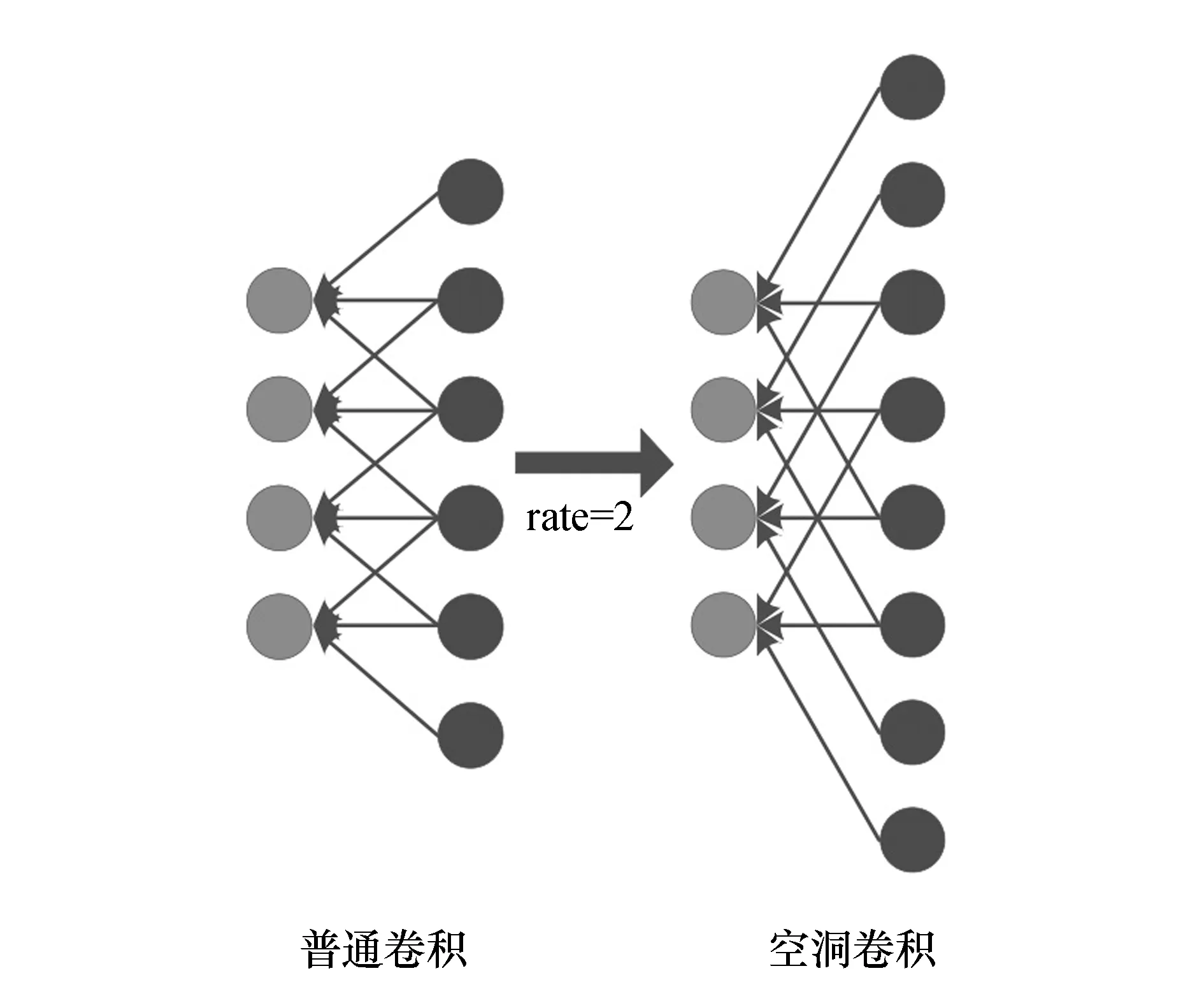
图2 普通卷积转化空洞卷积Fig.2 Ordinary convolution into dilated convolution

2 基于残差神经网络的滚动轴承故障诊断方法

2.1 改进的数据池化层

以往的观念中大的卷积核能带来更宽广的感受野，从而获得更多的特征信息，传统残差神经网络通过单个卷积层和池化层构建数据池化层，其中数据池化层采用的7×7卷积核更适用百万级的训练样本和多GPU运行才能完成的复杂结构的训练，由于大的卷积核会导致计算量的增加，参数量也将增多，然而滚动轴承的时域信号特征复杂且时变性强，更需要参数计算量较少且特征提取能力较强的数据池化层，因此采用7×7卷积核对于滚动轴承的故障诊断而言是不合适的.针对此问题，本文将7×7卷积层替换为3个3×3卷积层，3个3×3的卷积层串联带来的感受野大小相当于1个7×7的卷积层.假设当前卷积层的输入和输出的通道数(channels)都为N，当使用了3个3×3的卷积层时参数的数量为3×3×3×N2=27N2，但当使用单个7×7卷积层时参数的数量为7×7×N2=49N2，前者的参数数量明显更少，而且3个3×3的卷积层后面都使用ReLU激活函数，三个非线性激活层比单一非线性激活层对故障特征信息的提取能力更强.为了进一步提升该网络的提取速率加入批量标准化(BN);为了避免层数增多而导致出现过拟合问题，在3个卷积层之中加入残差连接结构.改进后的数据池化层结构如图3所示.

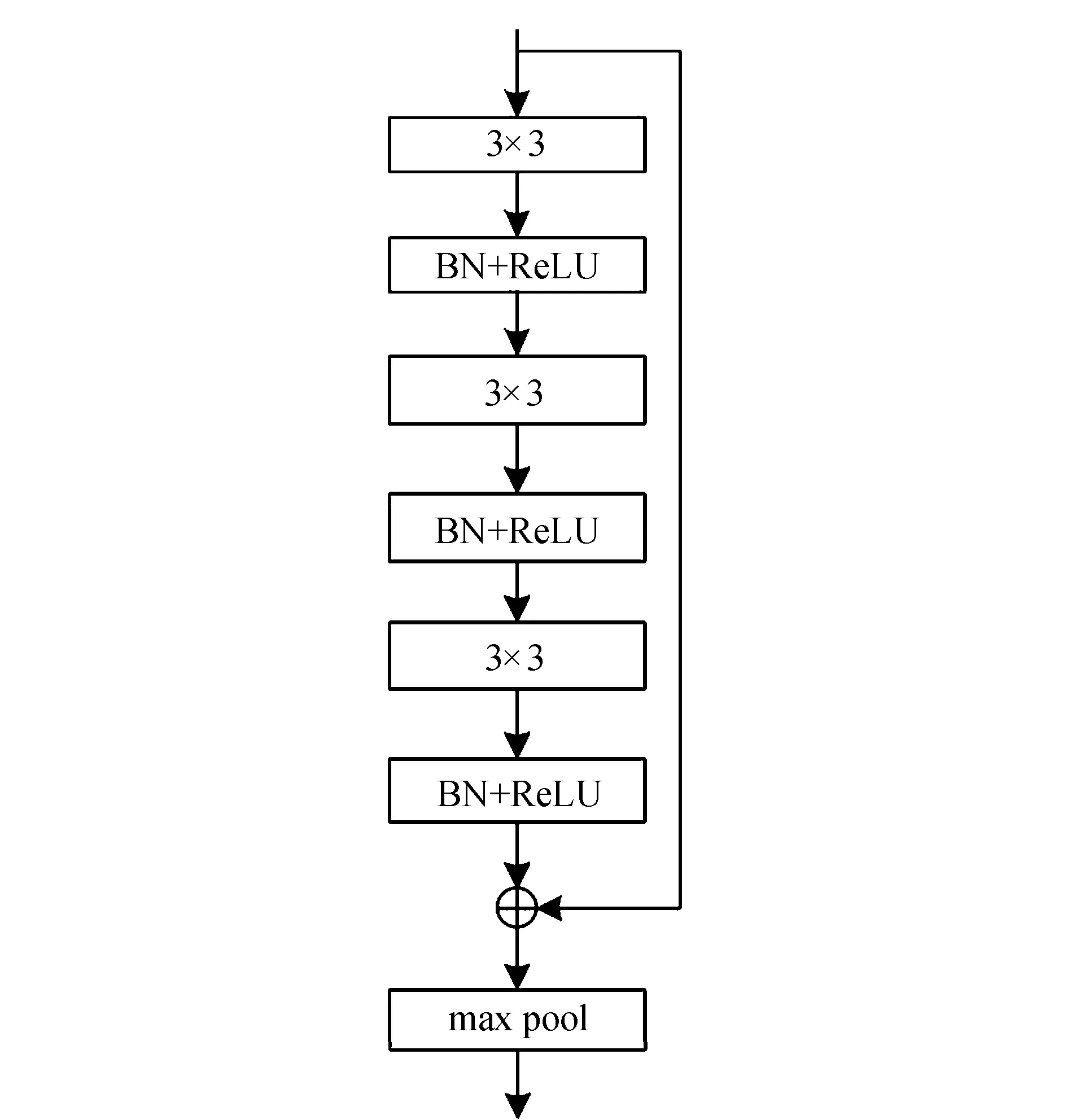
图3 改进的数据池化层结构Fig.3 Structure of improved data pooling layer

2.2 空洞残差块

由于不同工况下的轴承信号特征上具有差异性，采用传统残差块构建的残差神经网络难以准确识别轴承信号特征信息.针对此问题，本文将设计一种包含空洞卷积(dilated convolution)的空洞残差块.空洞卷积与普通卷积的卷积操作相同，但空洞卷积具有更大的感受野，并且在网络训练的过程中与后者具有相同的参数计算量.为了提高本文方法的特征学习能力，采用将残差块中普通卷积核替换为扩张率d=2的空洞卷积核的方式，构建空洞残差块，这样3×3的普通卷积核就具有了5×5空洞卷积核的感受野(receptive field)，具有更强的特征学习能力.空洞残差块的结构如图4所示.

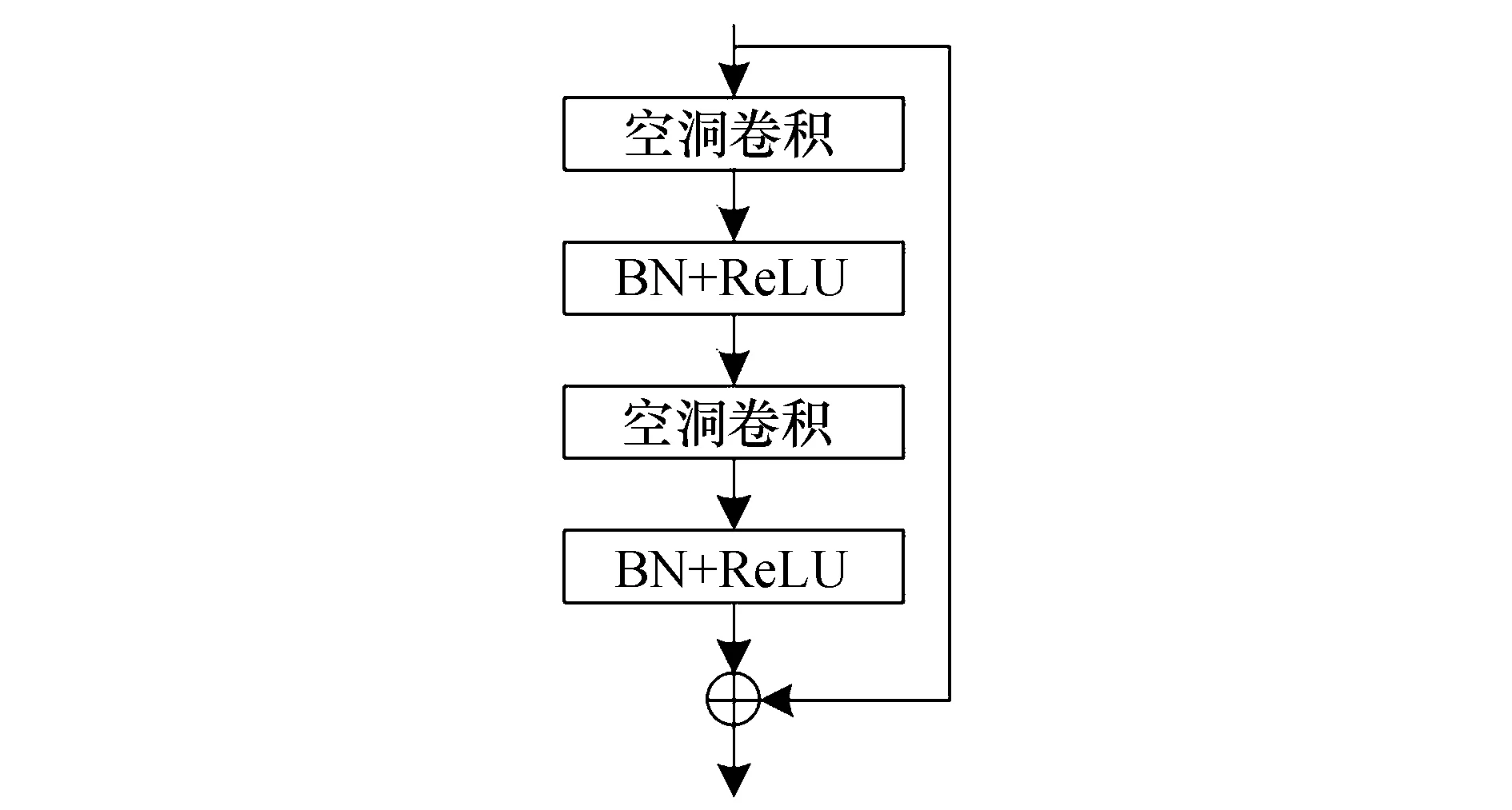
图4 空洞残差块结构Fig.4 Structure of dilated residual block

2.3 残差神经网络方法结构

针对滚动轴承工作环境复杂，有效数据样本不足导致的故障诊断效果不佳的问题,本文对传统残差神经网络进行改进，改进后网络共有13个卷积层，主要由5个残差块端对端首尾相连组成，该方法结构如图5所示.

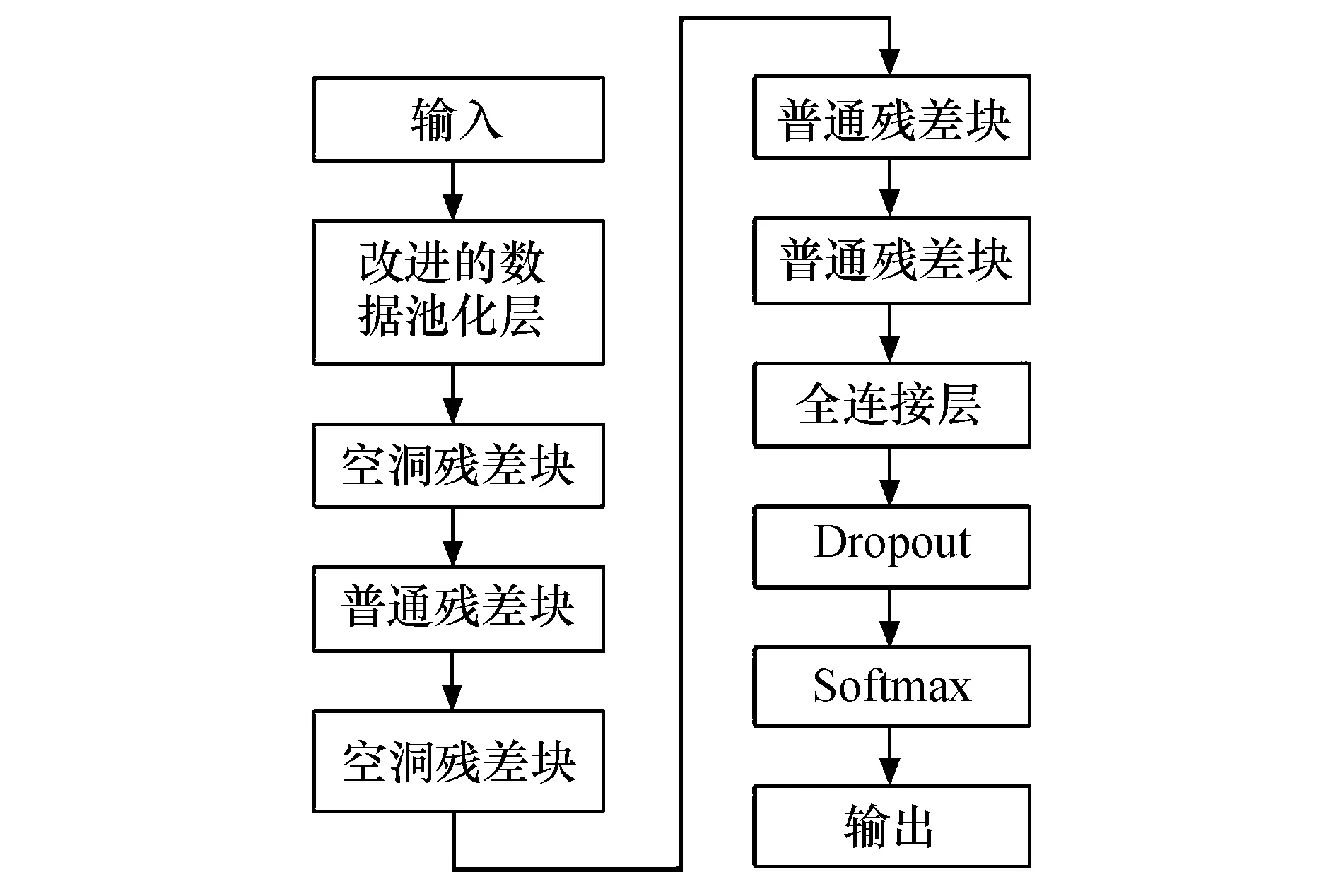
图5 残差神经网络方法结构Fig.5 Structure of residual neural network method

该方法首先将滚动轴承的输入信号转化为二维灰度图，通过由3个3×3卷积层组成的数据池化层提取该信号的特征信息；再经过5个残差块，本文设置每个残差块的卷积层均使用3×3的卷积核，分别将第一个残差块和第三个残差块设置为扩张率d=2的空洞残差块，提升该方法的特征信息学习能力，并在每个卷积层后加入批量标准化(BN)，在提升网络学习速率的同时提升了该方法的泛化能力；随后提取的数据经过全连接层，本文方法在全连接层后加入Dropout层.Dropout是一种有效缓解过拟合的方法，在训练过程中，Dropout会在每个训练批次中随机丢弃掉一定比例的神经元，使得残差神经网络仅对保留下来的神经元的参数进行前向传播及反向更新，从而达到正则化的效果，能有效地抑制过拟合带来的负面影响.设任一神经元的丢弃概率p为

(2)

其中：pa为样本a生成1的概率；Ba为第i类神经元中属于样本a的数量.通过这种方式可以减弱神经元间的相互作用以及对某些局部特征的依赖性，使得该方法在变工况故障诊断中不会受到过拟合的干扰，最后通过Softmax分类器输出诊断结果.此外，由于本文中提出的改进的数据池化层具有更少参数计算量，网络结构中使用残差连接使得特征传递方式更加便捷，所以改进的残差神经网络相比原残差神经网络在训练过程中具有较少的训练时间，更高的训练效率，同时参数量更少，占有的内存也更少.因此改进残差神经网络对算法复杂度的影响，无论时间复杂度还是空间复杂度都更加便捷.

2.4 基于残差神经网络方法的滚动轴承故障诊断流程

本文提出了一种基于残差神经网络的滚动轴承诊断方法，其故障诊断流程如图6所示.

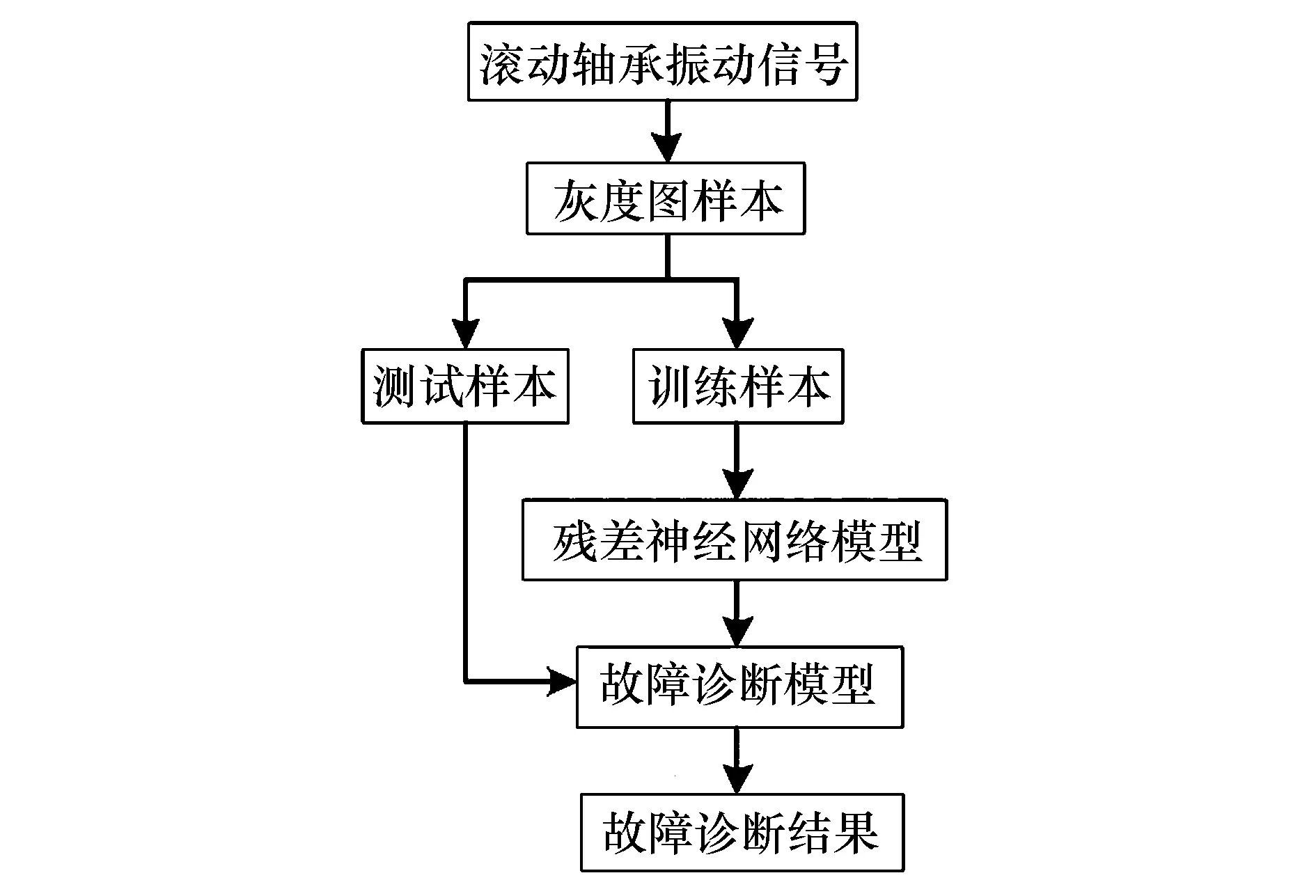
图6 残差神经网络方法故障诊断流程Fig.6 Fault diagnosis process of residual neural network method

在图6中，首先对采集的滚动轴承一维时域振动信号进行矩阵化，转化为二维灰度图样本；然后将二维灰度图样本按比例划分为训练样本和测试样本，将训练样本以批量方式输入到残差神经网络模型中，该模型经过多次训练和优化得到理想的故障诊断模型；最后将测试样本输入到训练好的故障诊断模型中，输出故障诊断结果.

3 实验仿真和结果分析

3.1 实验数据与设置

实验数据选用凯斯西储大学轴承研究所公开的滚动轴承数据集.该数据集是国际公认的用来验证轴承故障方法的标准数据集，被众多学者使用，因此使用该数据集进行仿真实验也更具有说服力.滚动轴承实验台如图7所示.

图7 滚动轴承实验台Fig.7 Rolling bearing test bench

实验选用电机驱动端为SKF6205型号的轴承，通过电火花放电的方式制造故障，故障位置分别在滚动体、内环、外环3、6、12点钟位置，故障直径分别为0.007、0.014、0.021、0.028 inch(其中，1 inch=2.54 cm)，来模拟滚动轴承不同程度的点蚀故障.根据不同位置不同损伤直径的故障，划分不同状态下的标签，包括：滚动体四种故障直径状态下四种标签，内环四种故障直径状态下四种标签，外环3点钟0.007 inch和0.021 inch故障直径状态下两种标签，外环6点钟0.007、0.014、0.021 inch故障直径状态下三种标签，外环12点钟0.007、0.021 inch故障直径状态下两种标签，以及正常状态标签，共16种状态标签.

滚动轴承在不同状态下的振动信号通过加速度传感器检测，并由采样频率12 kHz、采样通道为16通道的数据记录仪采集.电机驱动端的负荷有四种，分别为0、1、2、3 hp，对应的转速分别为1 797、1 772、1 750、1 730 r/min.其中，hp为英制的马力，1 hp=0.75 kW.对于每种状态下采集到的振动信号，采用一个步长为784个点的移动时间窗对其进行无重叠截取.设置训练样本和测试样本数目比为3∶1，为了获取变噪声测试样本，将不同信噪比(SNR,signal to noise ratio)的噪声加入到测试样本中，整个变工况数据集成分如表1所列.

表1 变工况数据集成分Tab.1 Variable working condition data set

仿真实验平台为TensorFlow，使用Python3.7编程，计算机处理器为i5-4200H，显卡为英伟达GTX860，系统为Windows10系统.实验采用小批量的训练方法，设置批大小64，迭代批数2 200，动态学习率的初始值设为0.001，衰减率设为每1 000次衰减0.9倍.训练过程中使用Adam梯度优化算法更新网络参数，并设置Dropout为50%的训练丢弃比率,在测试的过程中并不使用Dropout,即所有的神经元均参与计算.为防止实验结果的偶然性，选用10次实验结果的平均值作为最终结果.

选取基于人工滤波的SVM+EMD+Hilbert包络谱、BPNN+EMD+Hilbert包络谱方法[20]和基于深度学习的Resnet方法[21]进行对比实验.基于人工滤波方法的输入采用的是EMD分解后的前五个本征模态函数的包络谱，BPNN的结构设置为3 920-300-16，SVM多分类方式是“一对多”，并选用“高斯核函数”作为其核函数.基于深度学习的Resnet方法的网络结构由1个数据池化层、1个全连接层和5个残差块首尾相连构成，残差块均采用3×3大小的卷积核.

3.2 实验结果及分析

3.2.1变负荷故障诊断结果

滚动轴承在工作时，除了周围环境含有噪声，承载的工况也会发生变化，所以常用泛化能力来衡量滚动轴承诊断方法的变负荷诊断性能.对此，本文在变负荷的条件下对不同方法的性能进行实验，结果如图8所示.图8表示不同负荷变化下四种方法的故障诊断准确率，其中负荷变化是指选择0～3 hp负荷中的一种负荷数据作为训练集，选择另外一种负荷数据作为测试集.为了更直观地对比本文方法与其他三种方法的优势，以0-1、0-2、0-3三组实验结果为例进行分析，其中负荷变化0-1、0-2、0-3表示采用0 hp负荷下的数据样本进行训练，再以1、2、3 hp负荷下的数据样本作为测试样本进行变负荷故障诊断实验.

图8 变负荷故障诊断结果Fig.8 Result of variable load fault diagnosis

从图8可以看出，在0-1、0-2、0-3三组实验中,基于SVM+EMD+Hilbert包络谱和BPNN+EMD+Hilbert包络谱这两种方法诊断准确率均处于75%以下，基于Resnet的方法最高能实现92%的诊断准确率，而基于本文方法的三组实验诊断准确率均在90%以上.相比之下，本文方法的故障诊断准确率明显高于前三种方法.其原因为：基于人工滤波的两种方法因为存在包络误差、模态混淆等问题，不能够恰当处理复杂负荷下的故障；基于Resnet方法结构单一，对变负荷下的故障特征学习能力较弱；对比前三种方法，本文方法则具有较高的故障诊断准确率，原因在于在残差神经网络上改进了数据池化层，构建了空洞残差块的方法，并通过Dropout层削减了一些泛化能力较弱的故障特征，使得该方法在特征学习方面具有一定优势，能深度挖掘故障特征的内部信息，因此对于变负荷下数据特征的差异性具有更好的识别能力.此外，基于SVM+EMD+Hilbert包络谱、BPNN+EMD+Hilbert包络谱和Resnet这三种方法的诊断准确率在2-1、2-3这两组负荷变化的实验中故障诊断准确率有明显的提高，其原因是从2 hp负荷变化到1、3 hp负荷时，数据的表现形式比较相近，状态特征分布比较相似，所以故障诊断准确率得到了提高，但仍低于基于本文方法的故障诊断准确率.综上，本文方法更能适应变负荷下的滚动轴承振动信号的差异，具有更好的泛化能力.

3.2.2变噪声故障诊断结果

因为滚动轴承在工作运转过程中，零件震动以及相互摩擦会产生的噪声是不可避免的，并且会掩盖振动数据中的故障信息，所以滚动轴承故障诊断方法必须要具备一定的抗噪能力.为了体现本文方法在噪声复杂环境里具有更好的优势，将与选取的三种故障诊断方法对比分析，以2 hp、1 750 r/min负荷下滚动轴承故障诊断为例，在测试样本中分别加入信噪比为6、9、12 dB的高斯白噪声，然后用三种变噪声测试样本来检测每种方法的故障诊断准确率，结果如表2所列.

表2 变噪声故障诊断准确率Tab.2 Accuracy of variable noise fault diagnosis

从表2的数据可以看到，前两种基于人工滤波的SVM+EMD+Hilbert包络谱、BPNN+EMD+Hilbert包络谱方法故障诊断准确率明显低于基于深度学习的Resnet方法和本文方法，这是因为EMD方法虽然有良好的自适应性，但存在自身端点效应问题，不能有效地处理噪声数据.虽然Resnet方法的平均故障诊断准确率也较高，但随着信噪比减小，准确率会有所下降.而基于本文方法的变噪声故障诊断结果，在不同的信噪比下，故障诊断准确率高于其他三种方法，均保持在98%以上，并且在不同的信噪比下诊断准确率变化较小，其主要原因在于本文方采用残差快捷连接的同时，在全连接层后加入了Dropout层，所以能避免过拟合问题，取得了更好的诊断效果.由此可知，本文提出的方法在变噪声的情况下具有较好的抗噪能力.

3.2.3变工况故障诊断结果

滚动轴承常年工作在复杂的环境中，经常同时出现工况改变和噪声干扰，因此要求故障诊断方法不仅要在噪声干扰下保持稳定，而且要具备较强的泛化性能.对此，本文方法在变噪声、变负荷同时发生的环境中进行故障诊断实验，并与基于Resnet方法的诊断结果对比.图9表示在源测试样本加入的高斯白噪声分别为6、9、12 dB时，基于Resnet方法和基于本文方法对滚动轴承变负荷条件下的故障诊断结果，其中三种颜色的柱高分别表示不同信噪比下故障诊断的准确率，并对相同负荷变化下不同信噪比的柱高求平均值，作出平均值曲线.

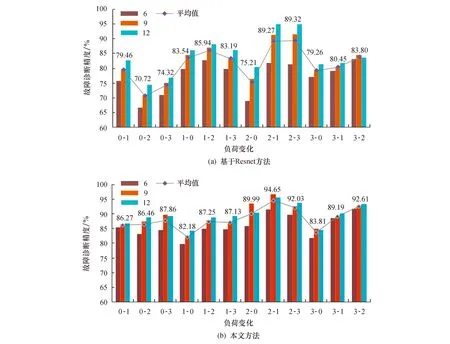
图9 变工况故障诊断结果Fig.9 Result of variable working condition fault diagnosis

首先分析不同负荷变化下的实验结果，以2-0组的实验结果为例，从图9a可以看出基于Resnet方法在该组实验中的三种柱高具有较大差距，而在图9b中基于本文方法在该组实验中三种柱高更加平稳，平均高度也高于前种方法.分析整个平均值曲线可以看出，图9a中平均值最高为86.57%，最低为71.96%，均值方差为0.001 7；而在图9b中，平均值最高为94.65%，最低为82.18%，均值方差为0.001 1；所以本文提出的方法整体诊断准确率更高，而且均值方差更小，随着工况的复杂化，仍然能保持较好的诊断效果.由此可见，本文方法在变工况的情况下具有较好的抗噪性和泛化能力.

4 结论

针对滚动轴承在变工况条件下时域信号中故障特征提取困难、故障诊断准确率低等问题，本文提出了一种基于残差神经网络的故障诊断方法.该方法的输入采用了滚动轴承时域振动信号，改进的数据池化层增强了数据特征的提取能力，并在残差神经网络中加入设计的空洞残差块提升特征学习效率，在全连接层后加入Dropout层避免过拟合带来的影响，最后通过分类器输出诊断结果.通过与SVM+EMD+Hilbert包络谱、BPNN+EMD+Hilbert包络谱和Resnet三种方法的实验对比，结果表明，本文提出的改进残差神经网络方法在变负荷的实验中能更好地适应负荷变化，在变噪声实验中具有更好的抗噪性，具有更高的泛化能力，最后在变噪声、变负荷同时存在的实验中仍然取得了较高的故障诊断准确率.