隐私保护下的车辆轨迹联邦嵌入学习与聚类

孔秀平,陆 林

(1.扬州工业职业技术学院信息中心,江苏 扬州 225127) (2.中电云数智科技有限公司,湖北 武汉 430056)

随着网联汽车的普及,车联网技术可以采集到大量的车辆时空轨迹数据. 对时空轨迹数据的挖掘和语义推理,既可以发现频繁的行驶路线或异常车辆,也可以帮助推理用户的出行意图,无论对物流行业、交管部门还是运营商来说,都具有很大的应用价值.

本文旨在利用某城市电动网约车实际运行数据,发现不同时段下的频繁运营路线,从而辅助智能交通决策与提升车辆运营效率. 发现频繁路线的通常做法是应用空间聚类算法[1],并将聚类的结果进行过滤得到满足要求的频繁线路. 但传统方法需要直接利用原始的轨迹经度、纬度数据来计算不同行驶轨迹之间的相似度,从而忽略了信息共享的隐私问题[2-4].

智能网联汽车的信息共享是富有挑战性的,因为人们日益感觉到数据安全和隐私的重要性[5]. 一般来说,不同渠道收集的不同车辆的状态数据、行驶轨迹都属于个人隐私,信息共享将带来安全隐私隐患. 另外,出租车、网约车包含乘客的敏感信息,例如住所、上班地和通勤路线等,这一事实需要在训练过程中考虑隐私.

针对这一挑战,一种可行的方法通过应用扰乱技术进行隐私保护式分布式聚类[6],但是其隐私保护程度有限. 另一种是通过潜空间表征[7],将原始轨迹压缩到统一维度的特征空间,表示为只有机器可以理解的特征向量. 然后再构建基于潜空间特征的机器学习算法,来解决相应的分类与聚类问题,从而避免对原始数据的直接利用敏感问题. 然而该轨迹表示的训练过程仍然需要数据拥有者分享自身的数据进行集中式学习,仍然存在隐私泄露的风险. 本文提出了一种差分联邦学习的轨迹嵌入学习方法,在充分保护用户隐私的前提下发现个体用户不敏感的频繁路线. 本文的主要贡献包括:

(1)提出了利用横向联邦学习框架在各方不共享原始轨迹数据的前提下,共同学习轨迹自编码模型.

(2)针对解码器可能还原具体用户原始轨迹的问题,利用差分隐私算法对模型进一步加密,避免模型参数泄露.

(3)在真实数据集上对差分后的轨迹嵌入进行了聚类分析,通过对比发现其聚类效果与无隐私保护的方法效果一致.

1 相关工作

1.1 基于轨迹嵌入表示的聚类

Yao等[8]尝试将每条轨迹转换成固定长度的表示形式,从而很好地编码对象的移动行为. 一旦学习到高质量的轨迹表示,就可以根据实际需要轻松地应用任何经典的聚类算法. Yue等[9]提出了一种用于移动行为聚类的无监督神经方法-DETECT. 它利用LSTM自编码[10]学习了行为潜在空间中轨迹的强大表示,从而使聚类算法(例如k均值)得以应用.

给定一个自编码模型M,它包括编码器Menc和解码器Mdec.该模型学习的目标是给定任意变长的轨迹序列x∈R,学习其定长的嵌入变量z∈Rd(d为嵌入空间维度)使得其尽可能包含原有轨迹的信息,表示为:

x≈Mdec(z=Menc(x)).

(1)

利用自编码模型将所有车辆的行程轨迹映射到嵌入空间Z后,就可以利用传统的聚类算法基于相似度度量进行自动分组. 每一组的中心向量,经过解码器还原后就代表了一条频繁的运行路线.

最新的实验结果表明,序列自编码已经是轨迹序列表征学习的state-of-art方法. 然而,上述研究中需要对所有车辆的轨迹进行集中学习,也就是所有车辆都要分享自己的GPS数据,这样明显暴露了各用户的相关隐私,比如家庭住址、上班场所以及通勤路线等信息[10].

1.2 基于差分隐私的联邦学习

联邦学习(federated learning,FL)[11-12]模式因其允许数据拥有者在不共享原始数据的前提下多方共同参与进行机器(深度)学习得到了广泛关注. 假设一共有n个数据拥有者,对应的数据集为D={D1,…,Dn},联邦机器学习的主要思想是每个数据拥有者k先接收第三方聚合者的初始化全局模型MFED,接着利用自身的数据进行本地训练得到局部模型Mk,然后仅通过传递参数来更新全局模型.聚合者接收数据拥有者的模型参数进行聚合,得到更新后的全局模型.该过程一直持续直到达到终止条件为止.

虽然联邦学习有效避免原始数据的传输和泄露,但是在深度学习模型的联邦训练过程中,仍然存在梯度泄露风险.针对这一问题,相关的研究利用差分隐私(differential privacy,DP)来解决. 差分隐私最早由DWORK[13]于2006年提出,典型的定义如下:

给定随机化算法A,对于任意两个相邻数据集D,D和A可能的输出O,算法A符合(ε,δ)-DP,满足

P[A(D)∈O]≤eεP[A(D′)]+δ.

(2)

式中,δ表示允许ε-DP被打破的概率,ε表示保护级别或隐私预算,ε越小表示隐私保护级别越高.此定义可确保基于算法的输出,对手具有有限的(取决于ε,δ的大小)识别任何个人存在或不存在的能力.

深度学习中实现DP的主要方式是对模型添加一定的噪声来满足[14].常用的噪声机制包括拉普拉斯和高斯噪声.以高斯差分隐私(Gaussian DP,GDP)为例,高斯机制从服从均值为μ,标准差为σ的分布 N(μ,σ2)中,随机采样添加到每一维的模型参数中.通过本地化差分隐私,每个客户端的梯度上传的第三方可以是不可信的.该梯度下降算法满足(ε,δ)-DP,最终模型参数的误差趋近于常数.相较于同态加密、密钥共享和混淆电路灯隐私保护技术,差分隐私因其计算和传输成本低的优势成为了联邦学习研究的新方向.

2 相关问题与研究方法

2.1 问题定义

定义1轨迹数据 考虑一组移动车辆集合,表示为V={v1,v2,…,vl}.某车辆的轨迹TR定义为其在时间维度上的一系列位置点.位置点为包含时间戳、经度和纬度的三元组,表示为p=.对于每个对象vi,其历史序列可表示为TRvi=(pi1,pi2,…,pim).

定义2周期时段轨迹 首先将车辆的轨迹点根据时间解析出所在星期,然后给定时间槽(表示为Δ),将该位置点映射到当天所在的时段.比如时间槽为0.5 h,那么一天被划分为48个时段.周期时段轨迹则是将车辆轨迹按星期时段维度进行分组得到的轨迹序列.

定义3轨迹嵌入表示 根据定义1和定义2,所有车辆的周期时段轨迹集用Ψ=(trip1,trip2,…,tripm)表示.因为轨迹的变长特性,我们定义轨迹的嵌入映射Ψ→Rm×d,其中R为嵌入空间,d为嵌入向量维度.经过该变换每一段轨迹都会被表示一个d维的向量表示.

基于以上定义,本文需要解决的问题是,给定任意周期时段内车辆的运行轨迹,找出其中的频繁路线.该问题的挑战主要是:(1)车辆原始轨迹不能分享以进行集中式的学习.(2)学习到的嵌入需要加密以保证个体用户的轨迹信息不被查询到.(3)最终聚类的效果要保证较高的精确度,即需要隐私保护和模型精度之间的折衷.

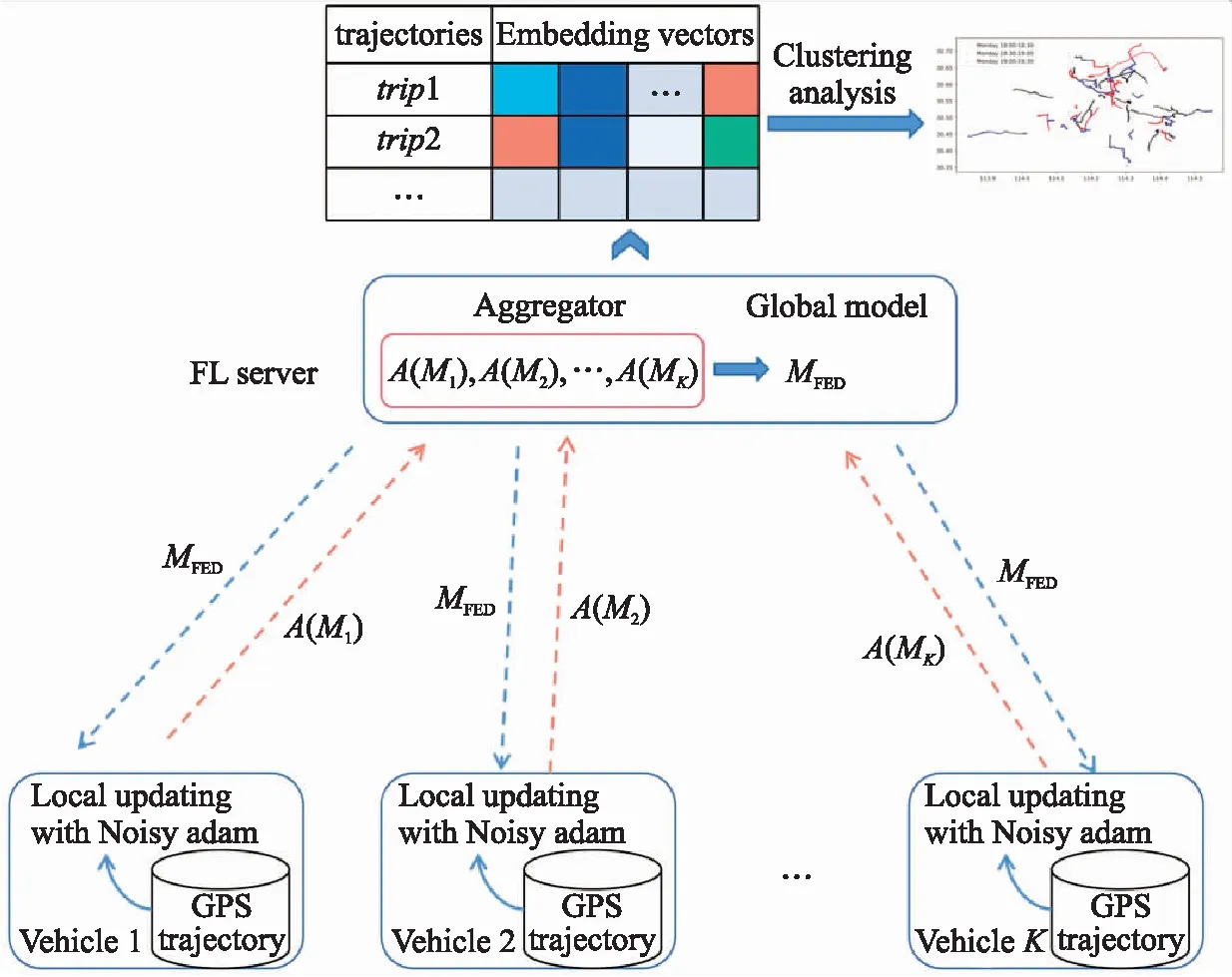
图1 差分隐私联邦轨迹嵌入聚类框架Fig.1 DP FL of trajectory embedding for clustering framework

2.2 轨迹嵌入的差分联邦学习框架

针对上述问题,本文提出了图1所示的差分隐私联邦轨迹嵌入聚类(DP FL of trajectory embedding for clustering,DP-FL-TE4C)框架. 图1主要包括了差分隐私联邦轨迹嵌入(DP-FL-TE)学习与轨迹嵌入聚类和解码两部分.

框架第一部分主要是包括一个第三方服务器(FL Server)和多辆车辆组成的联邦学习流程.这里假设车辆具有边缘计算能力,他们有选择地参与序列自编码模型的训练,并将添加噪声后的梯度上传给服务器.第三方服务器在云端进行云计算,它主导模型的联邦训练过程.它首先将模型及数据处理逻辑发送给图1中各个数据持有方,然后接收各本地结点训练好的模型参数,进行聚合得到一个全局最优的模型.

该框架第二部分的工作是FL Server接受各方发送的差分加密后的轨迹嵌入向量,应用无监督聚类算法得到频繁的簇,最后对频繁簇的中心嵌入向量应用解码器还原.

2.3 轨迹序列自编码模型

本文提出的框架中使用LSTM通过重建轨迹的GPS序列来生成固定长度的深度表示的嵌入向量. 在实践中,LSTM作为循环神经网络(RNN)的变体,通过加入门机制,能更好地捕获时序结构.

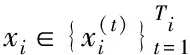
(3)

2.4 差分隐私联邦训练

本文提出的DP-FL-TE实现如算法1所示,它主要包括本地局部更新、差分隐私保护机制和云端模型聚合3个部分.

2.4.1 本地局部更新

2.4.2 差分隐私保护

对模型成功的攻击使攻击者能够与数据集中的具体记录建立链接,从而在记录包含敏感信息时导致隐私泄漏. 通过这些记录链接,可以根据乘客的轨迹分析出工作地点、家庭住址、活动模式和其他敏感信息. 本文与传统局部更新唯一的区别是采用Noisy Adam[15]算法来实现差分隐私,使得向FL Server分享的是隐私保护的模型信息.

2.4.3 云端模型聚合

服务器端接收到这K个模型参数后,通过聚合算法合并为一个全局模型MFed.本文采用经典的联邦平均方法来聚合.以第t轮联邦训练为例,云端接收K辆车的局部带“噪声”的参数并进行聚合方式为

(4)

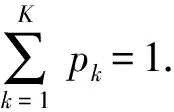
2.5 聚类分析

3 实验结果与分析

3.1 数据集与参数设定

本文使用一份真实数据集来进行测试,该数据集来自武汉市的88辆纯电动网约车,车辆GPS传感器每10 s获取当前的位置坐标. 数据跨度是从2018年3月1日到31日,共抽取到1 008条有效轨迹,这些轨迹几乎覆盖了城市所有主干道路,有利于发现用户不同时段的网约出行规律. 本文设置时段Δ=30 min,那样每个时段最多采集180条记录,也是自编码网络输入的最大序列长度. 整个数据集利用固定的随机种子进行二八划分,取20%放在云端server作为测试数据,剩余80%被划分到10(K=10)个客户端来模拟联邦学习.

本文采用了FedML框架进行仿真,利用Facebook开源的Opacus实现差分隐私,具体网络模型使用Pytorch来实现. LSTM编码器的输入为(180,2),输出的嵌入变量d为200,解码器输入输出与编码器刚好相反. 轨迹数据事先经过了归一化,故最后对解码输出加入了Sigmoid激活函数. 训练过程中的批大小为64,非DP的方法使用Adam优化器,学习率为0.001,局部迭代次数为20,最大轮询次数为1 000,损失函数使用均方误差(mean squared error,MSE).

图2 不同参与客户端数目下的模型在测试集上的 MSE效果对比Fig.2 Comparison of MSE on the test set of models with different number of participating clients

3.2 不同客户端的效果对比

首先,我们探讨了不同的客户数量对联邦模型在测试集上性能的影响. 仿真结果如图2所示,其中显然的NonFL-TE在测试集上的损失最低为0.013 8%. 其次,FL-TE最低的损失在0.07%左右. DP-FL-TE损失与FL-TE相关不大. 另外,可以看到随着客户端数目的增加,FLServer聚合的全局模型性能逐步提高. FL-TE和DP-FL-TE在客户端数目为9时验证损失最小.

3.3 训练过程对比分析

图3显示了3种模型在训练集上的平均训练损失情况. 可以看到,NonFL-TE模型收敛最快且训练损失最低. FL-TE收敛速度次之,因为其每次训练集的批次受限于本地数据集且利用联邦平均来优化多个局部模型. DP-FL-TE的联邦平均损失在前两轮急剧下降,最终收敛速度最慢,不过收敛时的训练损失与FL-TE相差不大.

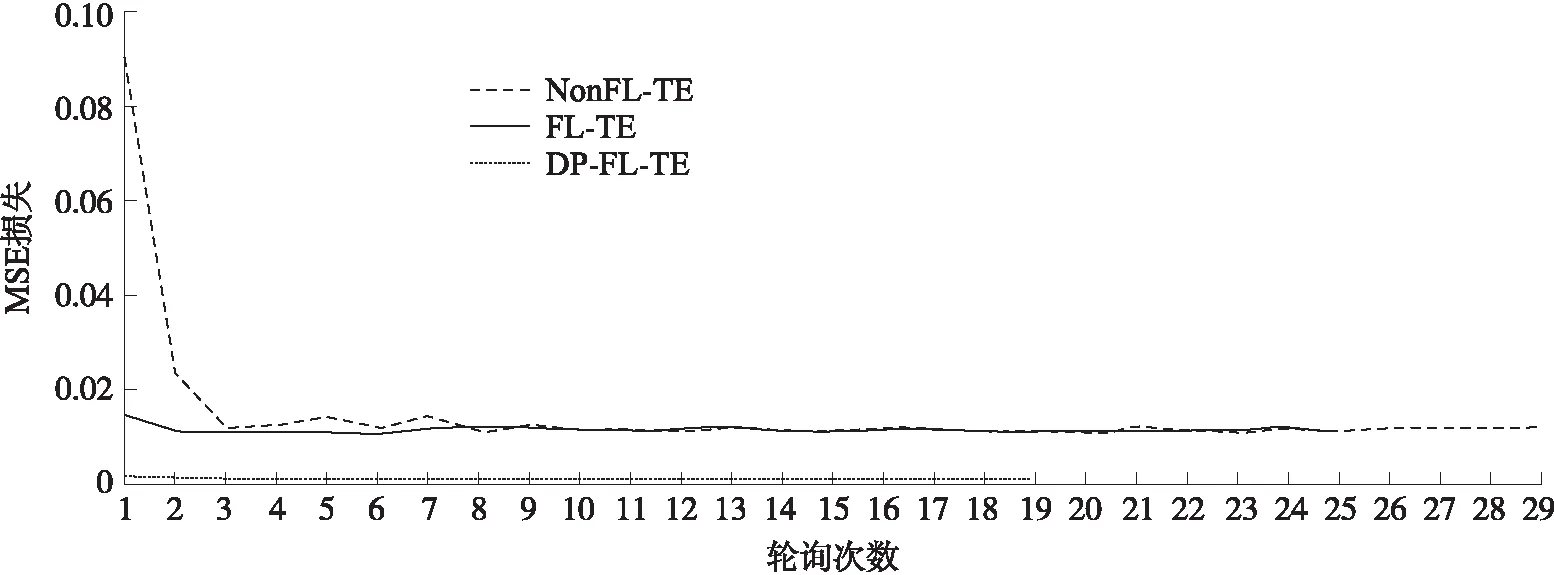
图3 不同模型的训练损失对比Fig.3 Training loss comparison of different models

我们观察到:(1)在差分隐私联邦模式下,聚合模型虽然精度有所损失,但最终依然能够有效地收敛. (2)模型精度的提高会导致隐私预算上升,也就是模型信息泄露的风险增加. 通过隐私分析结合训练损失,可以辅助确定两者的折衷点.

3.4 频繁轨迹聚类挖掘

本文的最终目的是对隐私轨迹进行聚类,对学习到的轨迹嵌入进行聚类,对比非联邦模式下的结果来验证DP-FL-TE的精度损失是否影响到最终聚类结果的有效性. 探索使用该框架来聚类将所有车辆轨迹数据,将相似的轨迹组合在一起,从而发现频繁行驶路线.

具体验证手段为,对3种模型输出的嵌入表示分别利用Gmeans算法进行自动聚类,最大簇数目为100,然后将聚类簇大小不小于10条轨迹的结果,作为频繁轨迹集合. 令3种模型输出的聚类结果分别为C,CFed,CDPFed,对应的轨迹嵌入矩阵为Z,ZFed,ZDPFed,然后将(Z,C)、(Z,CFed)、(Z,CDPFed)作为输入,使用Silhouette系数、Calinski Harabasz score(CH_score)和Davies-Bouldin score(DB_score)进行聚类效果验证. 这3种度量方法中,前两个方法的值越高表示聚类效果越好,第三个则相反.

表1中列出了这三种模型进行10次聚类后的结果. 可见,3种模型输出的频繁簇数目大致相近,且非联邦模型聚类效果最好. 以非联邦模型聚类结果为基准,可以发现联邦模型输出聚类结果在非联邦嵌入上的划分性能虽然有所下降,但下降幅度不大,且有趣的是DP-FL-TE4C稍微好于FL-TE4C. 这是因为一方面通过图3可以看到DP-FL-TE收敛时的训练损失水平与FL-TE模型的几乎相同,甚至略优. 另一方面,DP-FL-TE4C通过添加高斯噪声,使得轨迹自编码网络相对FL-TE4C具有更好的泛化能力,使得来自不同车辆相似的轨迹在潜空间上的生成表示更为接近.

表1 3种模型聚类效果对比Table 1 Comparison of clustering effect of three models

4 结论

本文提出了一种隐私保护的车辆轨迹深度表征框架. 该框架一方面使用序列自编码网络学习原始GPS轨迹的嵌入表示,解决了序列长度不一致(高维度)问题. 另一方面通过联邦学习模式避免用户隐私的直接暴露,并进一步利用差分隐私来避免模型参数的第三方攻击.

为了证明该框架的有效性,利用实际数据集通过联邦学习仿真,比较了该框架下模型的嵌入学习效果. 最后将其应用到实际场景中,通过对真实数据集上的轨迹嵌入学习以及聚类效果对比,可获得有用的频繁轨迹簇,即频繁路线.