用于单比特稀疏偶极子阵列波达角估计的协方差矩阵估计方法

程智勇,陈胜垚,吴 文,刘 中

(南京理工大学 电子工程与光电技术学院,江苏 南京 210094)

偶极子阵列是由可探测电磁波极化信息的偶极子矢量传感器组成的阵列。相较于传统标量传感器阵列,该阵列因获取了所接收电磁波所有的物理信息,具有抗干扰能力强、分辨能力高、检测能力稳健等优点,并且可以实现信号的极化编码[1]。但是,偶极子阵列对信号极化信息的探测是靠增加传感器数目实现的,导致系统开销大幅增长,限制了其在阵列规模较大、供电能力较低或成本限制较大的场景中的应用,例如,大规模多输入多输出(Multiple input multiple output,MIMO)雷达与无人机等。

在阵列信号处理[2,3]中,业已发展的单比特采样技术[4]与稀疏阵列技术[5-8]分别从采样和阵列结构的角度降低了阵列的系统开销。为了将偶极子阵列应用于更多系统开销受限的场景,文献[9]在偶极子阵列的基础上,提出了综合使用上述2种技术的单比特稀疏偶极子阵列,并给出了用于该阵列波达角(Direction of arrival,DOA)估计的单比特多重信号分类(One-bit multiple signal classification,OBMUSIC)算法。OBMUSIC的估计精度受到2个方面的制约:在单比特采样信号处理方面,该方法采用反正弦法则恢复归一化的无量化接收信号协方差矩阵,但是反正弦法则理论上仅适用于无限快拍场景,在有限快拍场景下其准确性没有理论保证;在稀疏阵列信号处理方面,该方法构造了稀疏阵列对应的差分阵列输出,而差分阵列消耗了接收信号的统计有效性[10],导致高信噪比下OBMUSIC的DOA估计精度远离其克拉美罗界。

业已发展的稀疏化方法为解决以上2个问题提供了新的解决方案。对于单比特采样信号的处理,文献[11]和[12]分别给出了基于凸优化和基于迭代硬阈值的信号重构方法,恢复了单比特压缩采样前的归一化信号;文献[13]和[14]给出了用于单比特采样的无网格稀疏线谱估计方法。以上方法均将单比特采样后的信号恢复问题或者参数估计问题转化为带有符号约束的凸优化问题求解,不依赖于信号的统计特性并与快拍数无关。对于稀疏阵列接收信号的处理,文献[15]和[16]将DOA估计问题转化为核范数与原子范数优化问题,摆脱了DOA估计对差分阵列的依赖;而稀疏参数化算法(Sparse and parametric approach,SPA)[17]和强化矩阵补全(Enhanced matrix completion,EMaC)算法[18]分别利用托普利兹矩阵和汉克矩阵的结构拟合稀疏阵列协方差矩阵。以上方法均将稀疏阵列的阵元视为空域的稀疏采样,并采用稀疏重构算法重构了具有同样自由度的均匀线阵的协方差矩阵,不需要构造差分阵列的输出,可同时有效抑制有限快拍误差。综合这2种解决方案,将单比特稀疏偶极子阵列的DOA估计问题转化为有符号约束的稀疏重构问题,可以重构有同样自由度的均匀线阵的归一化无量化接收信号协方差矩阵,从而有效抑制有限快拍误差,且避免了差分阵列带来的统计有效性下降。

本文针对单比特稀疏偶极子阵列的DOA估计问题,提出一种单比特稀疏协方差矩阵估计(One-bit sparse covariance matrix estimation,OB-SCME)算法。OB-SCME不使用反正弦法则恢复无量化接收信号协方差矩阵,亦不构造差分阵列输出,而是直接采用具有符号一致性约束与托普利兹结构约束的凸优化方法,减小了有限快拍误差,并恢复了具有托普利兹结构的接收信号协方差矩阵,提高了后续子空间类方法的DOA估计精度。首先,OB-SCME利用单比特稀疏偶极子阵列的结构,将该阵列的DOA估计问题转化为单比特稀疏标量阵列的DOA估计问题;然后,通过引入符号一致性的约束,将单比特采样协方差矩阵拟合问题转化为归一化无量化接收信号协方差矩阵拟合问题;随后,将该问题松弛为凸问题,并通过凸优化获得接收信号协方差矩阵估计的全局最优解。仿真实验表明,OB-SCME有效提升了单比特稀疏偶极子阵列的DOA估计精度,相较于OBMUSIC有较大的性能优势,特别是在低快拍场景下和互质阵上,其估计精度接近于采用无量化接收信号的MUSIC算法。

1 信号模型

1.1 稀疏偶极子阵列

偶极子传感器是将2个位置相同的单极化传感器(极子)正交放置构成的电磁矢量传感器。因2个极子分别探测x轴方向电场强度与y轴方向电场强度,所以被称为偶极子传感器。将L个偶极子传感器排布在x轴上,便组成了偶极子阵列。第l个偶极子的位置为ωlλ/2,其中,λ为波长,ωl∈S代表阵元位置,S为阵元位置的集合,称为阵元布置集。对于K个窄带电磁源,第l个偶极子的接收信号xl(t)[xl,x(t)xl,y(t)]T如下

(1)

Bkdiag(bk,x,bk,y)为偶极子响应矩阵,其中,而归一化DOA表示为第k个源的实际DOA表示为为第l个阵元的空间响应,sk(t)[sk,x(t)sk,y(t)]T表示入射信号矢量,加性噪声表示为nl(t)[nl,x(t)nl,y(t)]T。入射信号sk(t)的协方差矩阵为

(2)

式中:pk为入射信号的能量,εk,1、εk,2和εk,3是与信号极化状态有关的极化参数。本文对源与噪声做出以下假设:

(1)所有的K个源均为独立远场高斯源;

(2)每个源的DOA各不相同;

(3)所有的噪声独立且服从复高斯分布;

(4)噪声与源统计独立。

下文考虑阵列问题。当阵元布置集S为由0开始的连续正整数,即S={0,1,…,L}时,称该阵列为均匀线性偶极子阵列;而当S中的元素并不是连续的正整数时,称为稀疏偶极子阵列。较为常见的稀疏阵列布置集有2种,第1种由1个阵元间距为1、阵元个数为L1的均匀线阵与1个阵元间距为L1、阵元个数为L2的均匀线阵嵌套构成,称之为嵌套阵(Nested array)[5,6],其阵元布置集为

Sn={1,2,…,L1,L1+1,…,L2(L1+1)}

(3)

第2种稀疏阵列由阵元间距分别为L1与L2,阵元个数分别为L2与2L1-1的2个均匀线阵构成,其中,L1与L2互质,称之为互质阵(Coprime array)[7,8],其阵元布置集为

Sc={0,L1,…,L2L1,L2,…,2(L1-1)L2}

(4)

除此之外还有最小冗余阵[19]、超级嵌套阵[20]和最少孔洞阵列[21]等稀疏阵列。在后文中,为了表示简便,将具有阵元布置集S的阵列简称为阵列S,例如,将具有阵元布置集Sc的互质阵称为互质阵Sc。

1.2 单比特稀疏偶极子阵列

在稀疏偶极子阵列的基础上,2个单比特模数转换器(Analog to digital converters,ADC)被布置在同一个极子上,分别用于测量复信号的实部与虚部。因此,1个使用单比特采样的偶极子由4个单比特ADC构成,用于2路复信号的采样,称为单比特偶极子。将单比特偶极子按照稀疏阵列布置集S的形式布置在x轴上,即为单比特稀疏偶极子阵列。图1为单比特嵌套偶极子阵列,由6个单比特偶极子构成,阵元布置集为

Sn={1,2,3,4,8,12}

(5)

2个单比特ADC对1个复数c的采样可以表示为1个单比特采样算子作用在c上,其中,单比特采样算子signc(·)定义为

(6)

式中:cR与cI分别表示复数c的实部与虚部,sign(·)为作用在实数a上的符号函数,定义为

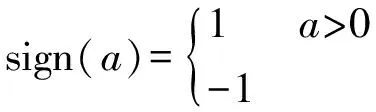
(7)

因此,阵列上第l个单比特偶极子的采样信号可以表示为

yl(t)=signc(xl(t))

(8)

图1 单比特嵌套偶极子阵列图

2 基于协方差矩阵估计的DOA估计

2.1 接收信号重排

有别于传统偶极子阵列DOA估计中的做法,本文分别考虑所有指向x轴的极子和所有指向y轴的极子。由图1可知,朝向不同轴的极子分别构成了2个阵元位置相同的标量阵。将朝向x轴的极子构成的标量阵的无量化接收信号记为xS,x(t),朝向y轴的极子构成的相应信号记为xS,y(t),则2个标量阵的无量化接收信号可以表示为

nS,x(t)

(9)

nS,y(t)

(10)

D={0,1,…,ωL}

(11)

则式(9)与式(10)可以表示为

(12)

(13)

由于xS,x(t)与xS,y(t)均为接收信号能量与1个相同的导向矢量的乘积,可以合并表示为

(14)

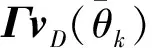
对于单比特稀疏偶极子阵列,根据式(8)中的单比特采样的定义,有

YS(t)=signc{XS(t)}

(15)

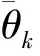
2.2 单比特采样协方差矩阵估计

对于有限快拍的场景,设快拍数为Z,则无量化接收信号可以表示如下矩阵形式

(16)

XS=ΓXD

(17)

标量阵D的采样协方差矩阵

(18)

(19)

式中:E{a}为随机变量a的数学期望,vec(·)为矩阵矢量化算符。使用广义最小二乘法求解RD的过程[22]可以表示为

(20)

式中:⊗表示克罗内克积。

式(20)可以进一步化简为

(21)

(22)

由式(8)可知,单比特采样保留了无量化接收信号的符号,因此可以直接根据式(8)建立如下的关系

signc(YS)=signc(XS)

(23)

(24)

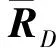
(25)

显然,式(25)中的3个约束项均为等式约束,这导致式(25)为非凸优化问题。不过,通过凸松弛的方式可以将式(25)松弛为凸问题,并通过半正定规划(Semi-deffinite programming,SDP)求解。

首先考虑式(25)中的最小化项。根据矩阵F范数的性质,可得

(26)

冷战是最伤人的，在婚姻中，要学会求同存异。有不同的看法或想法是很正常的事情，大方向是统一的就可以。夫妻间要经常坐下来交换意见，沟通思想，把心中的欢乐与苦衷倾诉出来。一旦在婚姻中爆发冷战，要学会主动向对方靠近，打破沉默。

(27)

(28)

根据矩阵Γ的结构,有

(29)

将式(28)、式(29)与式(27)带入式(26),可得

(30)

将式(30)与式(28)的左边部分带入式(25)可得

(31)

(32)

(33)

式中:⊙表示矢量的哈达玛积(Hadamard product),下标R与下标I分别表示相应矢量的实部与虚部。将式(32)与式(33)带入式(31),可得松弛后的凸优化问题

(34)

(35)

式(35)为典型的SDP问题,可以使用SDP算法比如SDPT3[25]求解u,进而获得归一化无量化均匀线阵接收信号协方差矩阵的估计T(u)。

2.3 DOA估计算法

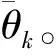
(1)构造信号YS(t)=[yS,x(t)yS,y(t)],其中,yS,x(t)与yS,y(t)分别为所有指向x轴的极子与指向y轴的极子构成的标量阵的接收信号。

(2)使用SDP求解算法求解式(35)获得u。

(3)通过u构造托普利兹矩阵T(u)。

(4)对T(u)进行特征分解,选择|D|-K个最小的特征值对应的特征矢量构造噪声子空间Un,其中,|D|表示集合D中的元素个数,即与稀疏阵S具有同样自由度的均匀线阵的阵元个数。

(36)

在此需要说明的是,步骤(4)与(5)为传统MUSIC算法,亦可使用其他利用采样协方差矩阵估计DOA的算法代替,例如root-MUSIC与旋转不变子空间(Estimation of signal parameters via rotational invariance techniques,ESPRIT)[26]等,仅需将此类算法作用于步骤(3)中得到的T(u)即可。

3 仿真实验与结果分析

3.1 实验设置

计算OB-SCME的仿真结果,并利用仿真结果验证所提算法的性能。在无特别说明的情况下,用于仿真的6阵元单比特稀疏偶极子阵列的布置集如下

Sn={0,1,2,3,7,11}

Sc={0,2,3,4,6,9}

(37)

式中:Sn为嵌套阵,Sc为互质阵。Sn由2个3阵元的均匀线阵嵌套组成,配置为L1=L2=3;Sc由L1=2和L2=3的2个均匀线阵组成。在实验中,所有的极化源信号的能量均为1,而且极化源信号的个数均已知。所有源信号的极化度以及极化参数均为其定义域内均匀分布的随机变量。每个极子上接收的噪声能量均相同。信噪比的定义为

(38)

(39)

实验运行在1台安装了Windows 10操作系统、2块INTER XEON E5-2660 v2 CPU(2.2 GHz*10*2核心)、56 GB内存的惠普工作站上。对于SDP问题的求解,使用了安装在MATLAB上的CVX凸优化工具箱中的SDPT3算法包。

在第3.3与3.4小节的实验中,选取了用于单比特稀疏偶极子阵列的OBMUSIC[9]算法作为对比,并且给出该阵列用于DOA估计时的克拉美罗界(Cramér-Rao bound,CRB)[9]以及用于无量化的稀疏偶极子阵列的MUSIC(Unquantilized MUSIC,UNQMUSIC)算法的估计性能[27]作为参照。

3.2 可分辨源数目

首先验证OB-SCME算法用于不同稀疏阵时可分辨的源信号个数。由前文可知,OB-SCME利用稀疏阵列S的输出估计与其具有相同自由度的均匀线阵D的协方差矩阵。这意味着,当OB-SCME用于单比特稀疏偶极子阵列S时,其可分辨源个数仅取决于S的自由度,即与S具有相同阵元间距与阵列长度的均匀线阵D的阵元个数,跟S的阵列类型无关。

如图2所示,绘制了嵌套阵上OB-SCME恢复协方差矩阵后的MUSIC谱,实验信噪比为10 dB,快拍数为50,采用了11个DOA不同的极化源。由图2可知,共计11个谱峰,这意味着对于自由度为12的嵌套阵,OB-SCME可成功分辨其能够分辨的最大数目的源。

图2 嵌套阵上OB-SCME的MUSIC谱

图3 互质阵上OB-SCME的MUSIC谱

同样绘制了互质阵Sc上OB-SCME恢复协方差矩阵后的MUSIC谱,如图3所示,信噪比与快拍数均与图2中相同,由于Sc的自由度为10,采用了9个DOA不同的极化信号。图2中共计9个谱峰,意味着OB-SCME成功分辨了9个源。与文献[7]中的OBMUSIC不同的是,OBMUSIC因采用了差分阵列的缘故,丢弃了互质阵的差分阵列孔洞之外的虚拟阵元,导致其阵列自由度下降。例如对于式(37)中的6阵元互质阵,因其8位置的孔洞,OBMUSIC仅可利用自由度为8的差分阵列,导致其可分辨源数目仅有7个。因此,相较于OBMUSIC,OB-SCME可以提高互质阵中的可分辨源数目。

3.3 估计精度与信噪比的关系

通过实验验证OB-SCME算法的估计精度与信噪比的关系。实验采用5个极化参数随机的极化源,其归一化DOA为[-0.25 -0.15 0.1 0.2 0.3],快拍数为60,信噪比从-10 dB升高至25 dB,每次升高5 dB,实验结果取200次蒙特卡洛实验的均值。

嵌套阵Sn上的实验结果如图4(a)所示,可观察到,OB-SCME的估计精度始终高于OBMUSIC,当信噪比为-10 dB与0 dB时,OB-SCME的估计精度有0.26 dB与6.2 dB的提升;当信噪比大于5 dB时,OB-SCME相对于OBMUSIC的估计精度优势较为恒定,平均为2.2 dB。相较于无量化测量的UNQMUSIC,OB-SCME的估计精度略低,当信噪比大于0 dB时,其精度低于UNQMUSIC,平均约2.5 dB。

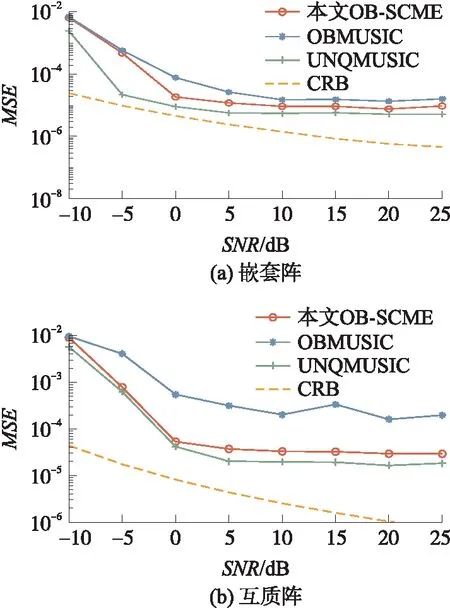
图4 2种阵列上MSE随信噪比变化图

互质阵Sc上的实验结果如图4(b)所示,与嵌套阵上不同,互质阵上OB-SCME相较于OBMUSIC的性能优势较大,当信噪比为0 dB、10 dB、20 dB与25 dB时,其精度提升分别为10.1 dB、7.8 dB、7.3 dB与8.3 dB。而OB-SCME的估计精度与UNQMUSIC较为接近,其估计精度差距平均为1.9 dB。该实验说明了,OB-SCME在互质阵上的优势大于其在嵌套阵上。

3.4 估计精度与快拍数的关系

通过实验验证OB-SCME算法的估计精度与快拍数的关系。实验中采用与上个实验相同的源,信噪比为10 dB,快拍数从20提高到100,每次提高8个快拍,实验结果同样为200次蒙特卡洛实验的均值。

由图5(a)可知,嵌套阵Sn上OB-SCME算法的估计精度在OBMUSIC与UNQMUSIC之间,当快拍数小于60时,OBMUSIC估计精度曲线在200次蒙特卡洛实验的情况下不够平滑,但是OB-SCME的估计精度曲线较为平滑,这说明了OB-SCME对极化度的鲁棒性较高。当快拍数大于60时,即OBMUSIC估计性能趋于稳定时,OB-SCME的估计性能领先OBMUSIC平均2.0 dB。而当快拍数大于44时,OB-SCME的估计精度与UNQMUSIC的差距较为恒定,平均为2.2 dB。

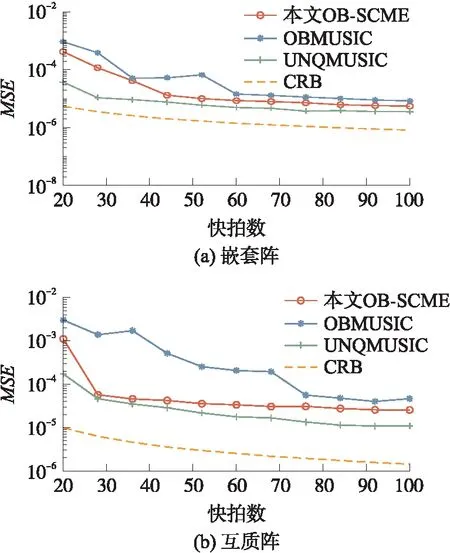
图5 2种阵列上MSE随快拍数变化图

由图5(b)可知,互质阵Sc上OB-SCME的估计精度同样在OBMUSIC与UNQMUSIC之间。但是,当快拍数小于68时,OB-SCME的估计精度相较于OBMUSIC有着大幅度的领先;随着快拍数的增长,OB-SCME的估计精度优势逐渐减小;当快拍数分别为28、44、60、76时,OB-SCME精度领先OBMUSIC分别为13.8 dB、10.9 dB、7.9 dB、2.6 dB。该现象说明了OB-SCME在低快拍下有着较大的性能优势。其原因为,OB-SCME为一种稀疏化的方法,对低快拍导致的信号统计有效性的降低并不敏感。而且,随着快拍数的增长,OB-SCME的估计精度与UNQMUSIC的差距逐渐变大,但是增长幅度不大。当快拍数分别为28、44、60、76、92时,该差距分别为0.9 dB、1.7 dB、2.8 dB、3.6 dB、3.7 dB。该现象进一步说明了,OB-SCME适用于低快拍场景下的互质阵。

4 结束语

本文利用单比特稀疏偶极子阵列接收信号的特征,将该阵列DOA估计转化为单比特稀疏标量阵的DOA估计。鉴于DOA估计精度与协方差矩阵的估计精度直接相关,利用单比特采样信号和无量化信号的符号一致性与标量均匀线阵接收信号的托普利兹性,将单比特稀疏标量阵的协方差矩阵问题转化为有约束的优化问题,并进一步将该约束问题松弛为可以使用半正定规划求解的凸问题进行求解,获得更准确的协方差矩阵估计值,从而改善子空间类DOA估计方法的性能。实验结果表明,在嵌套阵上,OB-SCME的估计精度MSE相较于OB-MUSIC有平均2.2 dB的性能提升;在互质阵上,由于OB-SCME成功利用了差分阵列孔洞之外的虚拟阵元,在提升了可估计源数目的同时,在不同点的信噪比下,其估计精度MSE平均提升了8 dB,当信噪比为0且快拍数少于60时,其估计精度提升可达10 dB以上,因此,OB-SCME更适用于低快拍的互质阵。