基于全变差模型与卷积神经网络的模糊图像恢复
2022-07-06况姗芸冯义东
杨 琼,况姗芸,冯义东
(1.琼台师范学院 信息科学技术学院,海南 海口 571127;2.华南师范大学 教育信息技术学院,广东 广州 510631; 3.海南师范大学 教育学院,海南 海口 571158; 4. 海南师范大学 数据科学与智慧教育教育部重点实验室,海南 海口 571158)
图像作为数据传输的介质之一,在很多领域得到了广泛应用,图像处理作为图像大规模应用的技术保证,成为近年来的研究热点。相比于文字数据,图像数据的解析更加复杂,其数据解析准确率与图像的分辨率、完整性等因素紧密相关[1]。在实际的图像数据生成、压缩、传输及解析过程中,由于受到噪声影响,以及图像分辨率低、部分图像缺失、自然退化等原因,造成图像数据的应用领域被限制,因此对模糊图像的复原处理显得尤为重要。通过图像复原技术,可以有效提升图像数据应用的适用范围,提高其在复杂环境中的数据保真[2],为图像数据分析提供有效技术支持。
当前,关于模糊图像恢复的研究较多。耿源谦等[3]采用非凸且非光滑的全变差(Total variation,TV)正则模型来实现图像去模糊,从而完成模糊图像复原。曹锦纲等[4]采用生成对抗网络不断对原始图像和复原图像进行优化,直至完成模糊图像复原。上述2种方法代表了当前模糊图像恢复的2种典型手段,前者采用正则化手段,后者采用深度神经网络方式,都达到了图像复原的目标。TV正则模型在模糊图像恢复中表现出较高的工作效率,适合于大规模图像粗略复原,而卷积神经网络(Convolutional neural networks,CNN)模型则精度高但复原效率低。因此,本文采取2种手段相结合的方法来充分利用两者优势。首先,通过卷积网络的卷积运算,有效运用图像数据的层级特征,挖掘图像细粒度特征,加强了对图像样本的分析适用性。其次,采用TV模型根据不同噪声类型选择合适的正则化模型,可以完成图像的粗略去模糊操作。本文算法将TV模型与CNN算法相结合,采用两级去模糊操作,旨在进一步提高模糊图像的恢复性能。本文的主要改进在于将TV正则模型和CNN模型相结合,在提高精度的同时没有大幅增加时间消耗。
1 基于TV模型的图像去模糊
TV模型通过正则化技术来实现模糊图像的去模糊操作。TV模型最重要的功能是能够有效修复模糊图像的细节部分[5],并能够保持差异边缘的高质量恢复。
设恢复的图像为x,模糊图像为f,经过TV模型处理的结果为[6]
(1)
式中:‖x‖TV表示TV约束,Φfid(x,f)表示TV保真,随机数μ>0。Φfid函数主要有2种表现形式[7]
(2)
(3)
式中:K为模糊参数,式(2)和式(3)分别表示全变分L范数(Total variation-L,TV-L)和TV-L2模型,2种模型的差异主要体现在不同噪声的模糊图像复原情况,它们分别用于处理高斯和方波噪声的图像恢复。
在TV-L2模型中,‖x‖TV的表示方法为[8]
(4)
在TV-L模型中,‖x‖TV的表示方法为
(5)
式中:xi,j表示图像x在像素坐标(i,j)处的值。通过TV模型式(1)的最小值优化求解,得到经过去模糊的图像。
2 模糊图像恢复
2.1 CNN算法
图像样本X=[x1x2…xN],m个图像特征经过第l层卷积可得[9]
(6)
式中:klj和blj分别为特征j至第l层的连接权重及偏置,*表示卷积运算,f(·)为
(7)
设卷积核尺寸h×w,选择最大值池化
(8)
令M=N/(h×w),X=[x1x2…xN]经过池化后的样本为X′=[x1x2…xM],X′进行卷积得到[10]
(9)
式中:∑aij=1,0≤aij≤1。
分别计算所有连接层卷积结果,然后进行分类预测。经过CNN运算,第k个节点的输出为yk,则误差[11]
δk=(dk-yk)yk(1-yk)
(10)
式中:dk为实际值。
CNN的权重更新方式[12]
(11)
当前权重wjk(n)调整后的权重
wjk(n+1)=wjk(n)+Δwjk(n)
(12)
偏置Δbk(n)的更新方式为
(13)
式中:α为更新步长,一般α=1。
当前偏置bk(n)调整后的偏置
bk(n+1)=bk(n)+Δbk(n)
(14)
所有节点的误差
(15)
当E满足设定的阈值时,算法停止,获得稳定的CNN模型。
2.2 模糊图像恢复流程
模糊图像经过TV正则粗略去模糊操作之后,对得到的图像进行分块,并通过CNN网络进行训练。设置合理的卷积核尺寸,将恢复的图像和原始清晰图像的各对应坐标的像素点对比,求解使误差和最小的CNN网络结构,获得稳定的基于TV模型和CNN的模糊图像恢复模型,具体结果如图1所示。

图1 基于TV-CNN的模糊图像恢复流程图
3 实例仿真
为了验证TV模型和CNN在模糊图像恢复中的可行性和有效性,进行实例仿真。模糊图像样本集来自于GoPro集,共3 214张照片,本文选择了该样本集的5个图像类别,具体如表1所示。首先对不同卷积核尺寸进行性能仿真,其次分别采用不同模糊核对原始图像进行模糊处理,验证TV-CNN算法应对不同模糊等级的图像恢复性能,接着对不同类别的噪声进行图像分析,最后采用不同图像恢复算法进行图像仿真。

表1 图像仿真样本表
图像恢复性能的评价核心指标为峰值信噪比(Peak signal-to-noise ratio,PSNR),其计算方法为
(16)
式中:n为每个像素的比特数,一般n=8,

(17)
除了PSNR,结构相似度(Structural similarity index measure,SSIM)性能也常作为图像恢复评价指标[13]。
3.1 不同卷积核尺寸的图像恢复性能
采用不同卷积和尺寸的CNN结构分别对表1中的5个样本进行仿真,验证其图像恢复性能。从表2可知,对于同类图像集,CNN的卷积核越大,TV-CNN的图像恢复PSNR和SSIM性能越差。当尺寸为2×2时,Bridge集的PSNR性能最优,为33.128 6;Face集次之,为32.537 5;最差的Billboard集为31.462 3。当尺寸为5×5时,Bridge集的PSNR性能为28.127 6,Face集为22.586 3,Billboard集仅为20.917 7。当尺寸由2×2增大为5×5时,恢复性能最好的Bridge集PSNR性能下降了15.1%,SSIM性能下降了12.7%;恢复性能最差的Billboard集PSNR性能下降了33.52%,SSIM性能下降了13.35%。这表明CNN的卷积核尺寸对模糊图像的恢复性能影响明显,这是因为卷积核尺寸越小,对图像模块的卷积运行粒度越小,参与卷积分析的图像成分越多,图像恢复的精度越高;反之,卷积核尺寸增大,参与卷积运算的粒度大了,图像恢复性能下降。因此,为了提高模糊图像的恢复性能,本文选择2×2的尺寸进行TV-CNN的图像恢复运算。

表2 不同卷积核尺寸的图像恢复性能表
3.2 不同模糊核的图像恢复性能
选择不同运动模糊核尺寸对原始图像进行模糊处理,然后分别采用TV-CNN算法对5类图像集进行图像恢复仿真,其主要性能统计结果如表3所示。
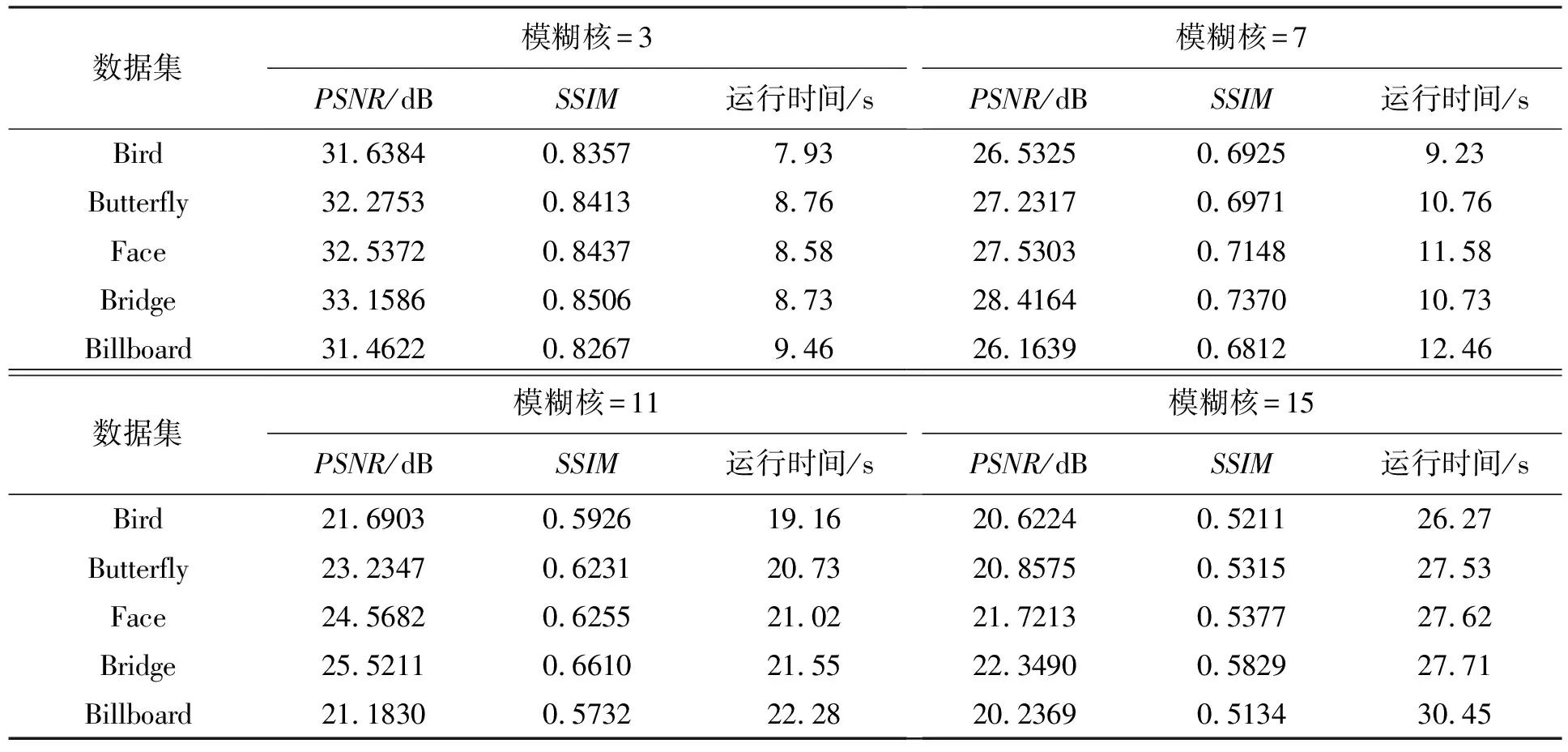
表3 不同模糊核尺寸的图像恢复性能表
从表3得,通过对原始图像进行不同尺寸的模糊核处理后,经过TV-CNN处理的图像恢复性能差异明显。对4类图像集横向比较发现,TV-CNN算法对Bridge图像集恢复性能最佳,Face集次之,Billboard图像集最差。对于同类别的图像集,PSNR和SSIM均随着模糊核尺寸的增大而减小,当模糊核尺寸为3时,5类图像集的PSNR均在31以上,而SSIM均在0.82以上,其中Bridge集获得了最高的PSNR值33.158 6 dB,最高的SSIM值0.8506;而当尺寸为15时,5类图像集的PSNR和SSIM分别下降至约20 dB和0.5。这主要是因为,模糊核尺寸的增加导致图像差异度边缘的模糊程度更高,图像恢复难度提升,所以图像恢复性能下降。
从TV-CNN的图像恢复运行时间来看,模糊核尺寸增加,图像恢复难度提升,TV正则优化求解时间加长,CNN迭代时间增加,因此对模糊图像的恢复需要更多时间。对比模糊核3和15,5类图像集的模糊图像恢复运行时间增加明显。
3.3 不同噪声的图像恢复性能
采用4种均值为0且方差不等的高斯噪声加入模糊图像,模糊核尺寸为3,卷积核尺寸为2×2,验证TV-CNN的图像恢复性能。
从表4得,通过对原始图像加入不同大小的高斯噪声,经过TV-CNN处理的图像恢复性能变化较大。5类图像集横向比较,TV-CNN算法对Bridge图像集恢复性能最佳,Billboard图像集最差。对于同类别的图像集,PSNR和SSIM均随着噪声的增大而减小,对比σ=0.01和σ=0.5,TV-CNN算法对5类图像集的PSNR和SSIM值差异显著,这是因为噪声增加导致有效图像信号的提取难度提升,在图像恢复时容易受到噪声干扰。
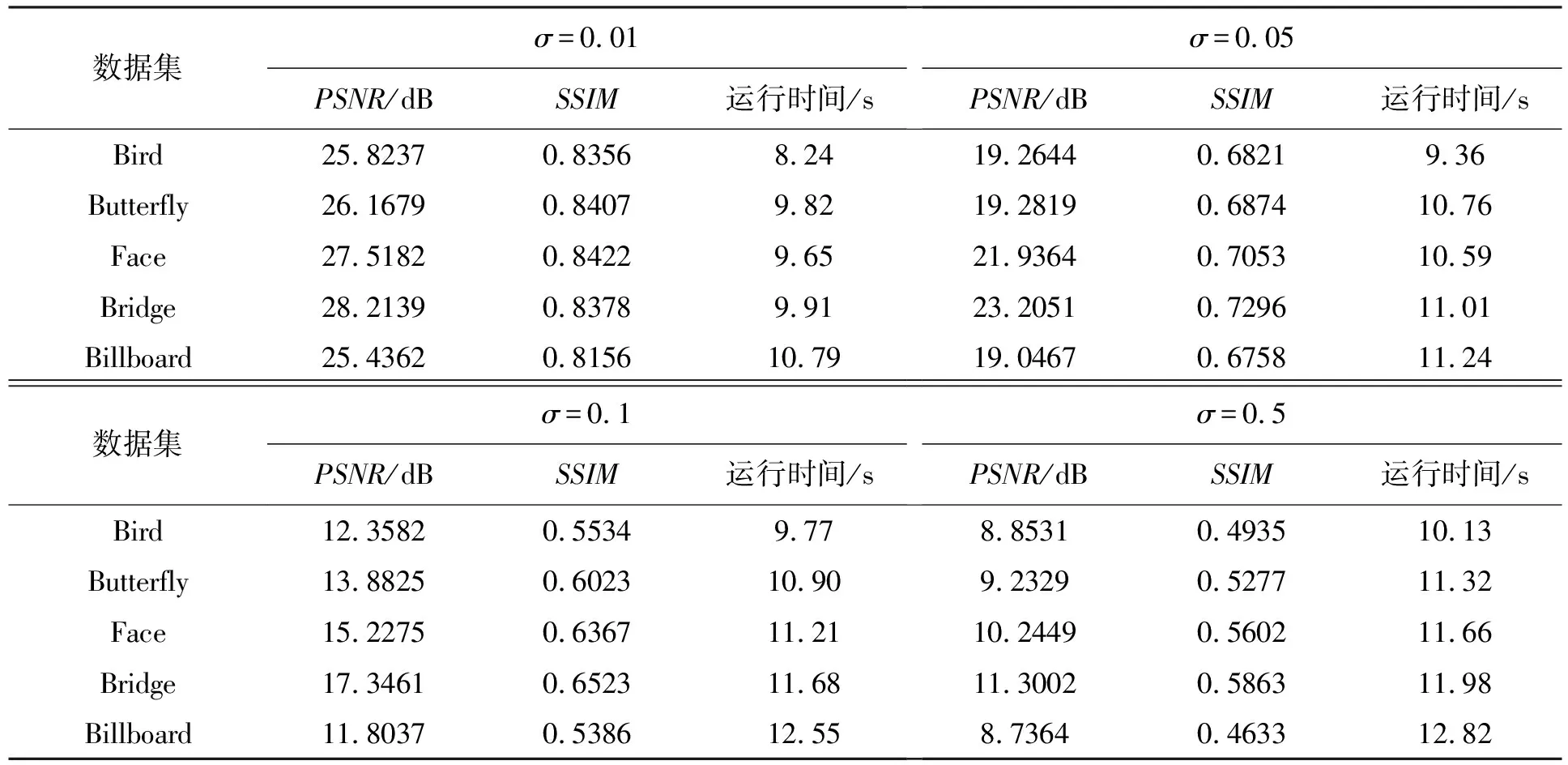
表4 不同噪声的图像恢复性能表
对比表3和表4可知,相比于模糊核尺寸,噪声对5类模糊图像样本的恢复性能影响更加显著,这说明在对模糊图像恢复之前,图像样本有效滤除噪声很关键,直接影响了图像恢复算法的执行效果。
3.4 不同算法的图像恢复性能
为了进一步验证TV-CNN算法对模糊图像的恢复性能,分别采用R-L(Richardson-Lucy)算法[14]、反向传播神经网络(Back propagation neural network,BPNN)[15]、生成对抗网络(Generative adversarial networks,GAN)[16]和TV-CNN算法对表1的5类图像样本集进行性能仿真,其中4种算法均选择模糊核3,高斯噪声σ=0.01,其图像恢复结果如表5所示。
从表5得,对于同一图像集,TV-CNN算法的PSNR和SSIM值最高,GAN次之,R-L算法最差。运算时间方面,GAN的图像恢复最耗时,BPNN和TV-CNN算法耗时很接近,这可能是因为GAN需要频繁的对抗比较,消耗了大量时间,而BPNN和TV-CNN均需要不断迭代获取稳定的网络参数,两者运算时间相差非常小。而5类图像集横向比较,4种算法均在Bridge集中获得了最优PSNR和SSIM值,Billboard集图像恢复的PSNR和SSIM值最低。从图像恢复时间来看,Billboard集最耗时,Bird集最省时,这表明4种算法对Bridge集的图像恢复适用性最高,Billboard集最差。以Billboard集为例,图像恢复性能的视觉比较结果如图2所示。

表5 4种算法的图像恢复性能表

图2 图像恢复性能的视觉比较结果图
综合比较,相比于R-L、BPNN和GAN算法,TV-CNN算法在公开图像集GoPro的5类图像样本恢复中均表现出了更高的恢复质量,该方法在模糊图像集的恢复中适用性更强。
4 结束语
采用TV-CNN算法进行模糊图像的恢复,通过TV正则策略和CNN卷积的2层图像去模糊操作,可以有效实现模糊图像的复原,并且获得较高的PSNR和SSIM性能,相比于常用模糊图像恢复算法,本文算法的PSNR和SSIM性能更优。后续研究将着力于解决包含噪声的模糊图像恢复问题,通过进一步优化TV-CNN算法的参数或者在TV-CNN运算之前进行有效的噪声滤除,提高TV-CNN算法对包含噪声的模糊图像恢复问题的适用性。
