基于柔性动力学仿真的齿轮拓扑优化

苏成龙 罗肇艺 糜沛纹 秦国锋 曹兰

广西师范大学 广西桂林市 541004

1 前言

齿轮在传动系统中属非常重要的部件，传动较为平稳，传动比精确且效率较高；随着工业制造的进步，齿轮的性能研究也逐渐增加，对设计出性能良好、强度较高且质量轻的齿轮有着较高的要求；齿轮的拓扑优化设计是目前最常用的优化方法，通过改变结构布局，获得较佳的性能与体积质量。

目前，姚廷强等人对刚性与柔性的齿轮进行动力学建模分析，得出柔性齿轮更符合实际传动的结论。高海龙等人基于多体动力学对柔性体齿轮副进行仿真，在动力学仿真过程中考虑了柔性体的自身变形对系统的影响。薛云伟对齿轮进行轻量化设计、动力学分析与拓扑优化等，达到满足强度与轻量化的要求。兰州研究齿轮等传动系统等设计的理论和方法，提出了采用齿轮参数多目标优化和齿轮幅板结构拓扑优化两步减重的设计方法。

2 建立齿轮模型

使用UG 软件建立啮合齿轮，模数为2.5，齿宽为16mm，主动齿轮为17 齿，从动齿轮为47齿，传动比为2.76；啮合齿轮如图1所示。

图1 啮合齿轮

3 齿轮柔性化

使用Hypermesh 软件将齿轮转换为柔性体，生成MNF 中性文件，所选择的材料为45 号钢，45 号钢的力学性能如表1 所示；

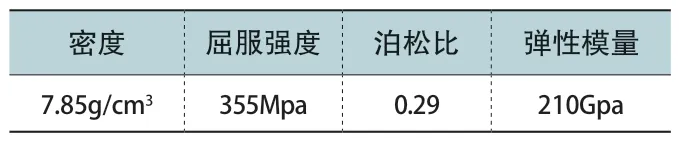
表1 力学性能

4 齿轮动力学仿真

动力学仿真得出一定负载和一定工况下的碰撞啮合力、转矩以及角速度的数据；本文对啮合齿轮的仿真分析采用刚性对刚性、刚性对柔性、柔性对柔性的三种耦合仿真，选取最接近理论值的耦合仿真方案。

4.1 理论计算

4.1.1 碰撞参数计算

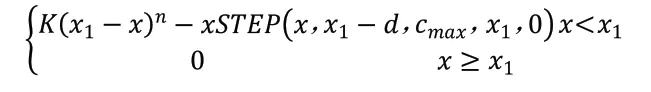
上式中，K 为刚度系数，n 为接触指数，x为接触距离，d为穿透深度，c为阻尼函数，当接触距离x 小于接触函数的距离变量x时，产生接触力；当接触距离x 大于接触函数的距离变量x时，接触力为零。

接触刚度的表达式为

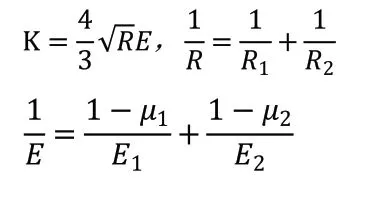
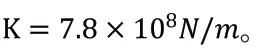
在设置接触中，力指数取1.5，阻尼取5×10N·s/m，穿透深度取1×10m，静摩擦因数取0.1，动摩擦因数取0.06，静平移速度取0.1m/s,摩擦平移速度取1.0m/s。

4.1.2 啮合力理论计算

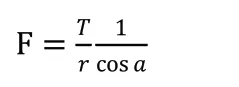
其中，T 为输入的转矩，r 为从动轮的半径，α 为压力角，故将设置的数值T=100N/m，r=0.05875m，α=20°代入公式中，计算得碰撞啮合力的理论值为F=1810.77N。

4.1.3 转矩理论计算

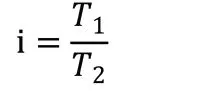
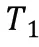
4.1.4 误差值

4.2 齿轮动力学仿真

将啮合齿轮导入Adams View 中，设置重力为9.80665N，单位制选择MKS，积分求解器选择WSTIFF，积分格式选择SI2，添加驱动与接触，输入转矩为100N/m，设置阶跃函数，STEP（time,0,0d,0.1,1000d），仿真终止时间设为0.5 秒，步数设为1000 步。

4.2.1 啮合齿轮刚性耦合

齿轮仿真分析，如图2 所示；查看转矩情况，齿轮在啮合过程中，曲线图变化较大且不规律，转矩最大值为229.26N/m，平均值为42.21N/m，如图3 所示。

图2 齿轮刚性耦合仿真

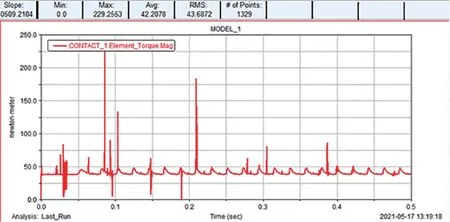
图3 齿轮转矩曲线图

对数据结果进行分析，如表2 所示。

表2

4.2.2 啮合齿轮刚柔耦合仿真

刚柔耦合齿轮仿真分析，如图4 所示。查看转矩情况，转矩曲线趋于平缓，运动呈规律性，在0-0.5 秒的传动中，转矩最大值为69.38N/m，平均值为39.41N/m 如图5 所示。

图4 齿轮刚柔耦合仿真

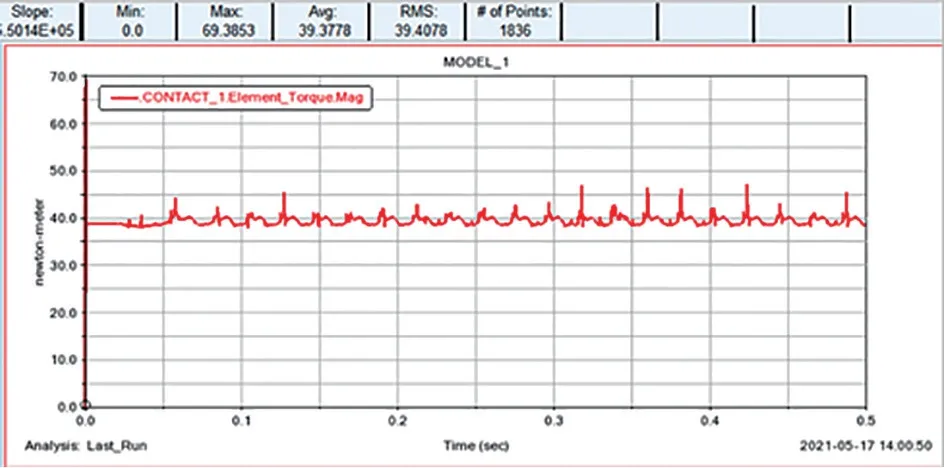
图5 齿轮转矩曲线图

对数据结果进行分析，如表3 所示。

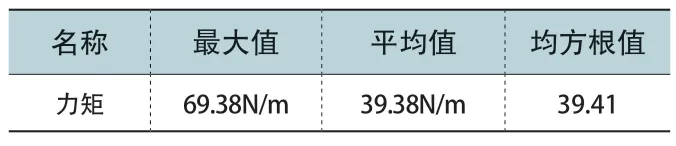
表3

4.2.3 啮合齿轮柔性耦合仿真

柔性耦合齿轮仿真分析，如图6 所示。查看转矩情况，转矩曲线基本呈直线状态，在0-0.1 秒的传动中，转矩最大值为403.88N/m，平均值为37.20N/m，如图7 所示。

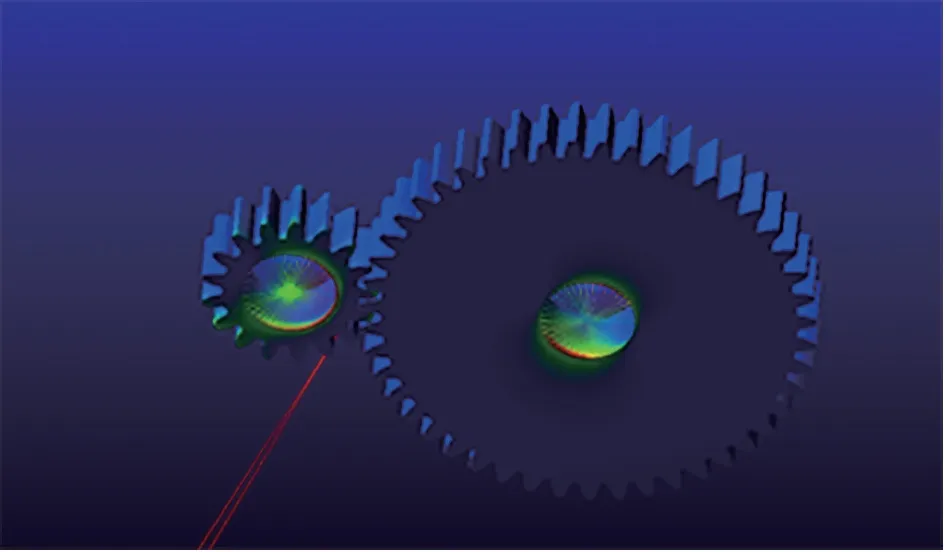
图6 齿轮柔性耦合仿真

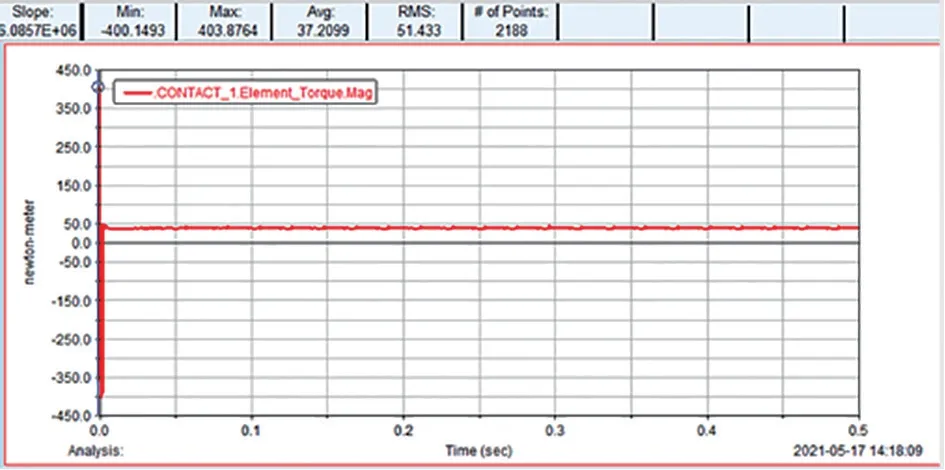
图7 齿轮转矩曲线图

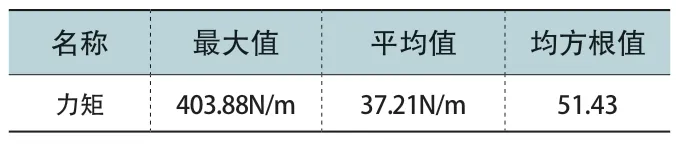
表4

4.2.4 结果分析

通过啮合力和转矩的理论计算得到理论值为1810.77N 与33.90N/m，将数值代入误差计算中，结果如表5所示。

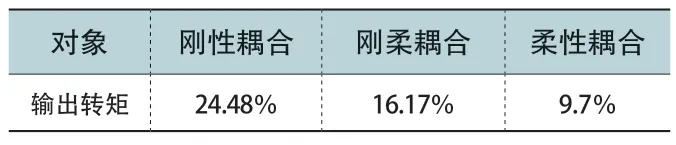
表5

通过曲线图得知，齿轮在进行啮合时，刚性耦合模型碰撞最大，其次到刚柔耦合模型，最小是柔性耦合模型，说明柔性耦合模型在齿轮传动过程中是最平稳的；无论是刚性耦合还是刚柔耦合，柔性耦合模型是最接近理论值的；因此，柔性齿轮啮合传动更合乎齿轮的传动特性。

5 齿轮拓扑优化

本次拓扑优化的载荷条件的设置是基于齿轮三种耦合模型的动力学仿真，在齿轮的动力学仿真中已经证实柔性齿轮是最符合实际的，柔性齿轮可以通过其优越的弹性形变能力吸收部分碰撞能量，从而达到减轻碰撞的效果，所以考虑以柔性耦合的最大输出转矩作为拓扑优化的边界条件，柔性耦合模型中的最大输出转矩为403.88N/m。

赋予齿轮材料属性为45 号钢，先划分2D 网格，再对网格进行拉伸，手动划分的网格可以对轮齿处进行细化，可以提高有限元分析的准确性；在齿轮内圈施加刚性接触，约束刚性单元，仅开放绕轴的自由度，对其中一个轮齿面施加固定约束，如图8 所示。添加设计变量为design，考虑到在求解过程中载荷分布不均会导致优化后的材料分布不均，结构混乱，故要添加一个竖直方向的拔模约束和周向对称的几何约束，响应量为柔度响应com 与体积响应vol，设置工况以后定义优化以后的体积分数为70%，即保留30%的体积，优化结果如图9 所示。

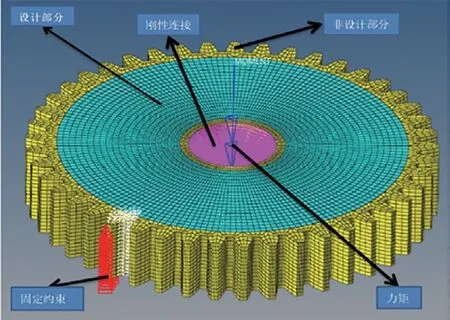
图8 有限元分析模型

图9 齿轮拓扑优化

拓扑优化前后质量变化（kg）如表6 所示。

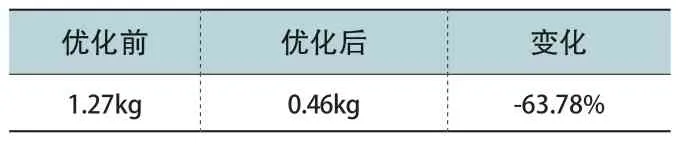
表6

6 齿轮静力学分析

在拓扑优化完成后我们需要对优化前后的齿轮模型做一个强度对比，此项工作是基于啮合齿轮的动力学仿真，以齿轮啮合传动时所受到的圆周力、径向力为载荷条件，以应力、振动位移为研究对象。

齿轮所受到的径向力与圆周力。现计算在动力学仿真中齿轮所受到的径向力与圆周力大小，径向力与圆周力的公式为

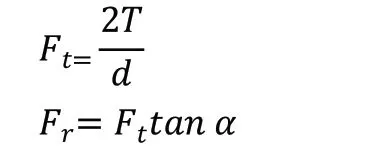
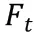
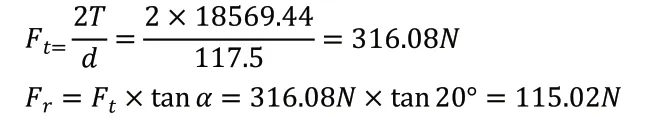
故可以得到径向力为115.02N，圆周力为316.08N。至此，分析的载荷条件已经计算完毕。现对齿轮进行载荷的施加，对轴心处的刚性连接点施加固定约束，对其中一个轮齿施加圆周力与径向力，如图10 所示。

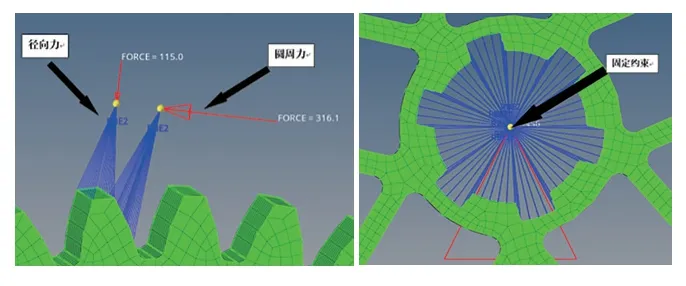
图10 边界条件施加

查看位移云图，最大位移量为0.07mm，作用在轮齿处，如图11 所示；查看应力云图，最大应力为318Mp，作用在齿根处，如图12所示；从结果可以看出，位移量可以忽略不计，最大应力不超过45 号钢的屈服强度，说明拓扑优化的合理性。

图11 位移云图

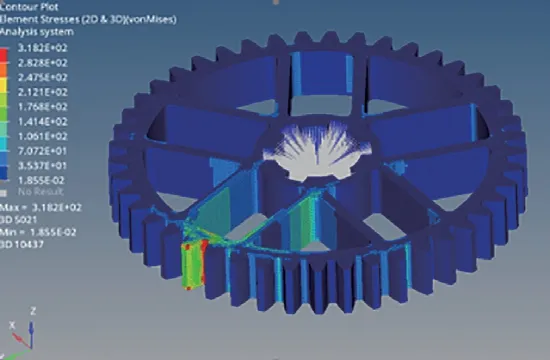
图12 应力云图

7 结论

在齿轮副的动力学仿真中，通过刚性耦合、刚柔耦合、柔性耦合模型的仿真对比，柔性体相对于刚性体的误差明显减小，分析结果与理论计算比较接近，可以发现齿轮柔性化后得到的数据更为准确，能够使齿轮拓扑优化的准确性提高，更为接近实际值，对于齿轮的拓扑优化有更大的提升空间。