基于0-1 规划的企业原材料的订购与运输模型

2022-07-06李阳刘玉祥任家璇

时代汽车 2022年14期

李阳刘玉祥任家璇

石家庄铁道大学交通运输学院河北省石家庄市 050043

1 引言

某企业每周能生产2.82 万m的产品，可供企业选择的原材料有A、B、C 三类，其中每生产1m产品所需A 类原材料0.6m、或B 类0.66m或C 类0.72m。企业的主要目标是在48 周的生产周期前制定24 周的原材料订购和运输的优化方案，同时在实际生产时尽可能使原材料的库存量可供两周的生产需求，同时企业对供应商实际供给的原材料企业全部接收。为保证企业的生产效益，原材料的采购成本也须考虑，A、B、C 三类原材料的采购单价比为 1.2：1.1：1.0。三类原材料运输和储存的单位费用相同。

分析402 家供应商的供货特征，确定保障企业生产的50 家最重要的供应商。基于该问题，为满足生产需求，确定企业应至少选择的供应商的个数，针对这些供应商为企业制定未来24周每周最经济的原材料订购方案，进而制定损耗最少的转运方案。

2 模型的建立与求解

2.1 熵权法确定指标权重

熵权法是一种在综合考虑各因素提供信息量的基础上计算一个综合指标的数学方法。在构造出指标评价体系后可分别得到402 家供应商的三项指标值，为了综合三项指标对供应商作出评价，本文采用熵权法分析的三个指标的权重。

表1 各项指标权重

2.2 问题二模型的建立与求解

2.2.1 数据分析与处理

将供应商的供货量按供给原料种类分为三大类。得到A、B、C 三类原材料对应的供应商分别有146、134、122 家。每家供应商对应有240 周的供货量。因为企业每次生产前需要制定24 周的原材料订购和转运计划，于是猜想供应商供货量随周数存在周期变化关系。为验证此猜想，可参考问题一的求解结果，从50 家重要供应商中筛选任意几家进行检验，发现供应商供货量与周数的确存在周期性。其中S040与S055 的供货量随周数变化的周期性较为明显。

将5 年的数据（供货量与运输损耗率）分为10 组，每组包含24 周。基于上述分析处理建立规划模型求解下列问题。

2.2.2 满足企业生产需求的规划模型

企业每周的产能为 2.82 万m，同时为了保证正常生产的需要，该企业要尽可能保持不少于满足两周生产需求的原材料库存量。假设在制定未来24 周的订购与转运方案时，企业仓库已无库存。A、B、C 三类原材料对应的供应商按周均可分为10 组。以生产 A 类原材料的供应商为例进行分析：10 个组中每个组第一周的供货量求和取均值，将该值作为未来24 周第一周的供货量，同理可得未来24 周的其它周的供货量，在计算中发现，若供货量取均值时，即使所有供应商供货，也不满足生产条件。因此取每个组中的最大的供货量作为未来24周的供货量。在计算中发现，第七周的全部供货量也不能满足生产需要，针对此周对约束条件做出了调整，据此建立单目标规划模型如下：

Step 1：建立0-1 规划模型、确定变量

仍然对生产A 类原材料的供应商分析（B、C 同理），根据上述分析可得到146 家供应商在未来24 周所能提供的最大供货量。可分别构造A、B、C 三类供应商与周数的最大供货量矩阵M ,M ,M，其中行代表每家供应商、列代表周数。而在实际供应中，每家供应商每周是否对企业供货是未知的，为简化这一问题，本文引入0-1 决策变量矩阵：β ,β ,β（注：0-1 矩阵与最大供货量矩阵行列意义相反）。β=1表示供应商给企业供货，β=0表示不供货。

设n,n,n分别表示提供原材料A、B、C 的供应商数量，分别为146、134、122；表示满足企业生产需求的供应商的数量，为目标变量。

Step 2：目标函数

企业应确定满足生产需求的最少供应商的数量，故选择满足企业生产需求的供应商的数量作为目标变量，求其最小值。目标函数的每一部分分别为给企业供货的三类供应商的数量。

Step 3：约束条件

企业每周的产能已知，同时为了保证正常生产的需要，在实际生产时尽可能使原材料的库存量可供两周的生产需求。假设在制定未来24 周的订购与转运方案时，企业仓库已无库存，因此需要在第一周前就买好前两周的原材料作为库存，则第一周需要买第三周的材料、第二周需要买第四周的材料、以此类推。最终，将0-1 矩阵与最大供货量矩阵的乘积记为矩阵。

2.2.3 最经济的原材料订购规划模型

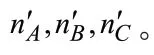
Step 1：建立模型、确定变量

问题二第一问中0-1 矩阵已经按供给原材料的种类对128 家供应商作了分类，按此分类构造企业未来24 周订货量的矩阵E,E,E。为目标变量，它表示企业未来24 周总订货量的采购成本。

Step 2：目标函数

企业需要确定未来24 周每周最经济的订货量。将每周的订购成本求和即可得到24 周订货量的总成本。最经济说明采购成本最低，故该规划问题为求最低采购成本的问题。题目中未给出各原材料的具体成本，但为了量化分析，可根据它们的成本关系，可假定A、B、C 的单价分别为1.2 元/m、1.1 元/m、1元/m。于是得到如下最低采购成本的目标函数。