开放式喷漆室通风方式的优化研究

贾圣孔，田 宏，朱家鑫，王成龙 （沈阳航空航天大学安全工程学院，辽宁沈阳 110136）

0 引言

涂装是将涂料涂覆于基底表面形成具有防护、装饰或特定功能涂层的过程，其中使用最多的方式是喷涂[1］。在喷漆过程中部分溶剂会挥发出来，随着气流流动，即便VOC（挥发性有机化合物）浓度较低，长期接触仍会对人体的皮肤、呼吸系统以及中枢神经系统产生不同程度的伤害[2-4］。职业卫生调查表明，喷漆室内涂装作业普遍存在VOC浓度超标的现象，特别是在通风不畅的情况下超标现象更为严重[5-6］。

开放式喷漆室具有构造简单，安装方便灵活，费用便宜以及能耗较低等特点，目前国内一些企业开始逐渐采用开放式喷漆室。开放式喷漆室由于一端开放及进风口是确定的，使用机械排风来排除室内的VOC时，其排风方式就显得十分重要。为了验证不同的通风方式对喷漆室内VOC含量的影响，本研究以某型号开放式喷漆室为实例，对其一侧排风（分为有利工况与不利工况）、直线式排风以及两侧排风3种通风方式在不同的换气次数下，采用计算流体力学的方法来模拟其通风效果，以便优化其通风方式。

1 开放式喷漆室的结构

以美国Marathon开放式喷漆室（用于汽车维修涂装）为研究实例，喷漆室规格为6.4 m×5.5 m×3.4 m，内部建有汽车与人体模型，尽可能贴近现实中喷漆室内部物体布置，以保证模拟条件与实际相符。第1种模拟方式为一侧式排风方式，即从开口（5.5 m×3.4 m）自然进风，有利工况从前侧条形排风口（5 m×0.5 m）排风，不利工况从后侧条形排风口（5 m×0.5 m）排风；第2种模拟方式为直线式排风方式，即采用从开口自然进风，对侧条形排风口（5 m×0.5 m）排风；第3种模拟方式为两侧式排风方式，即从开口自然进风，两侧（各为5 m×0.25 m）条形排风口排风，见图1。

图1 开放式喷漆室结构图以及3种模拟通风方式Figure 1 Structure diagram of open spray booth and three simulated ventilation methods

喷漆枪口直径为1.6 mm，处于人体模型前方0.7 m处。在涂装作业中，从喷枪口喷出的漆雾是室体内部VOC的主要来源，油漆中的树脂、溶剂、助剂等都含有固定的配比，通过比例即可计算出漆雾中的VOC含量[7］。为简化计算模型，本研究假定喷漆室内的VOC均为从喷枪口流向室内，并以用甲苯作为研究对象来进行模拟，即假定从喷枪口喷向室内的全部为甲苯。

2 数值计算方法

2.1 控制方程与计算模型选择

喷漆室内部气流组织涉及到多种气体的流动，但相互之间并不涉及到化学反应，因此采用不开化学反应的组分输运模型，该模型可通过计算不同组分的对流、扩散及反应源的守恒方程来模拟化学组分的混合与输运[8］，适用于计算喷漆室内各种气流组织的流动情况。喷漆室内的流动控制方程包括连续性方程（质量守恒方程）[9］、动量方程[10］、组分输运模型[11-12］以及可实现k-ε湍流模型[13-14］。

连续性方程：

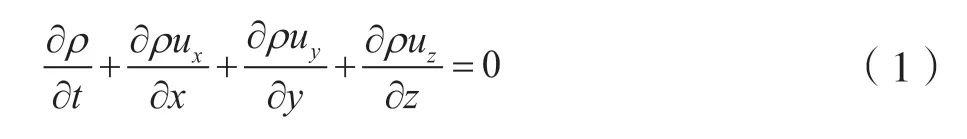
式中：ρ—密度，kg/m3；t—时间，s；u—各方向上的速度，m/s。

动量方程：

式中：p—静压，Pa；τij—应力张量，Pa；gi— 方向上的重力加速度，m/s2；Fi—外部体积力，N/m3。

组分输运模型：

式中：Yi—第i个组分的局部质量分数；Di—第i个组分的扩散系数，m/s2；Si—源相，kg/（s·m3）；Ri—化学反应中生成物组分i的净生成率，kg/（s·m3），本研究中由于不考虑气体之间的化学反应，因此Si和Ri取值为0[15］。Sct为湍流施密特数，Sct=μ/ρDi，其中，μ为湍流黏度，Pa·s。

可实现k-ε模型：

式中：k—湍流动能，m2/s3；ε—湍流耗散率，m2/s3；μt—湍流黏性系数，Pa·s；σk与σε是k和ε传输方程的普朗特数，分别取1.0与1.2，S—应变速率，s-1；C2=1.9。

2.2 网格及定解条件

由于喷枪口直径较小，因此在枪口附近进行网格加密，并逐步以1.2的增长率增大网格尺寸，同时对流场梯度较大位置，如进风口与排风口同样使用网格加密，在其他的变化比较缓慢的区域，使用较为稀疏的网格。

喷漆室内部流场可以视为稳定的不可压缩的湍流流动，在计算域中将送风口设定为压力入口；将喷枪口设定为质量流量入口，质量流率为0.001 kg/s；将排风口设定为速度入口，由于系统默认速度方向指向计算域，因此在设定时要在速度前面加一个负号来调整混合空气的方向；对于图1中其他未指定的边界，均设定为壁面边界，并且认为光滑无滑移。在计算过程中不涉及温度的变化，即默认为喷漆室内温度恒定。

在仿真计算过程中，采用双精度的分离隐式算法求解器，压力和速度的耦合采用SIMPLE算法，方程组的离散格式采用二阶迎风格式，时间离散格式采用二阶隐式格式，计算结果中变量残差均降至1×10-4以下。

3 网格验证及仿真设计

3.1 网格无关性验证

计算前需要排除网格数量对于计算结果的影响，为此采用网格划分工具来对模型进行网格划分，对于边界中的压力入口、质量流量入口以及速度入口进行网格加密。根据喷漆室的实际情况，采用直线式60次/h的换气次数进行网格验证。分别划分了103万、172万以及424万3种不同数量的网格。并选用喷漆室内从坐标（5.7，2.75，0）到（5.7，2.75，3.4）这一条线上的速度分布情况来判断网格的独立性，结果如图2所示。由图2可知，3种网格之间的差别并不大，尤其是172万与424万网格之间的差距更小，但考虑到计算时间的问题，选用网格数为172万的划分方式较为合理。

图2 网格独立性验证Figure 2 Grid independence verification

3.2 模拟方案

针对一侧式（分为有利工况与不利工况，其中：有利工况为喷枪口与排风口位于一侧；不利工况为排风口位于喷枪口的对侧）、直线式以及两侧式3种通风方式，分别进行了60次/h、70次/h以及80次/h各3种换气次数的模拟，共计12种工况。具体如表1所示。

表1 模拟工况Table 1 Simulated working conditions

针对上述12种工况的模拟结果进行评价，选用瞬时捕集效率[15-16］与排污效率[17］作为评价指标，其中瞬时捕集效率为在t时刻排风口处排出的VOC气体与喷枪口处的VOC散发量的质量流量之比，即

排污效率（η）为排风口处污染物浓度（Ce）和进风口处污染物浓度（Co）之差与室内平均污染物浓度（Cz）和进风口污染物浓度（C0）之差的比值，等式如下：

因进风口处为从室外吸入的空气，几乎不含污染物，因此可以认为C0为0，由此，上式可化简为η=Ce/Cz。一般情况下，排风口处的污染物浓度总是要比室内的平均污染物浓度高，所以排污效率的值总是要大于或等于1[18］。

4 模拟结果分析

4.1 流体域浓度场变化

非稳模拟结束后，采用后处理软件将计算结果绘制成图，图3为工况1（直线式60次/h）条件下，zx面上y=1.75 m以及yz面上x=1.7 m处的VOC浓度随时间变化的情况。

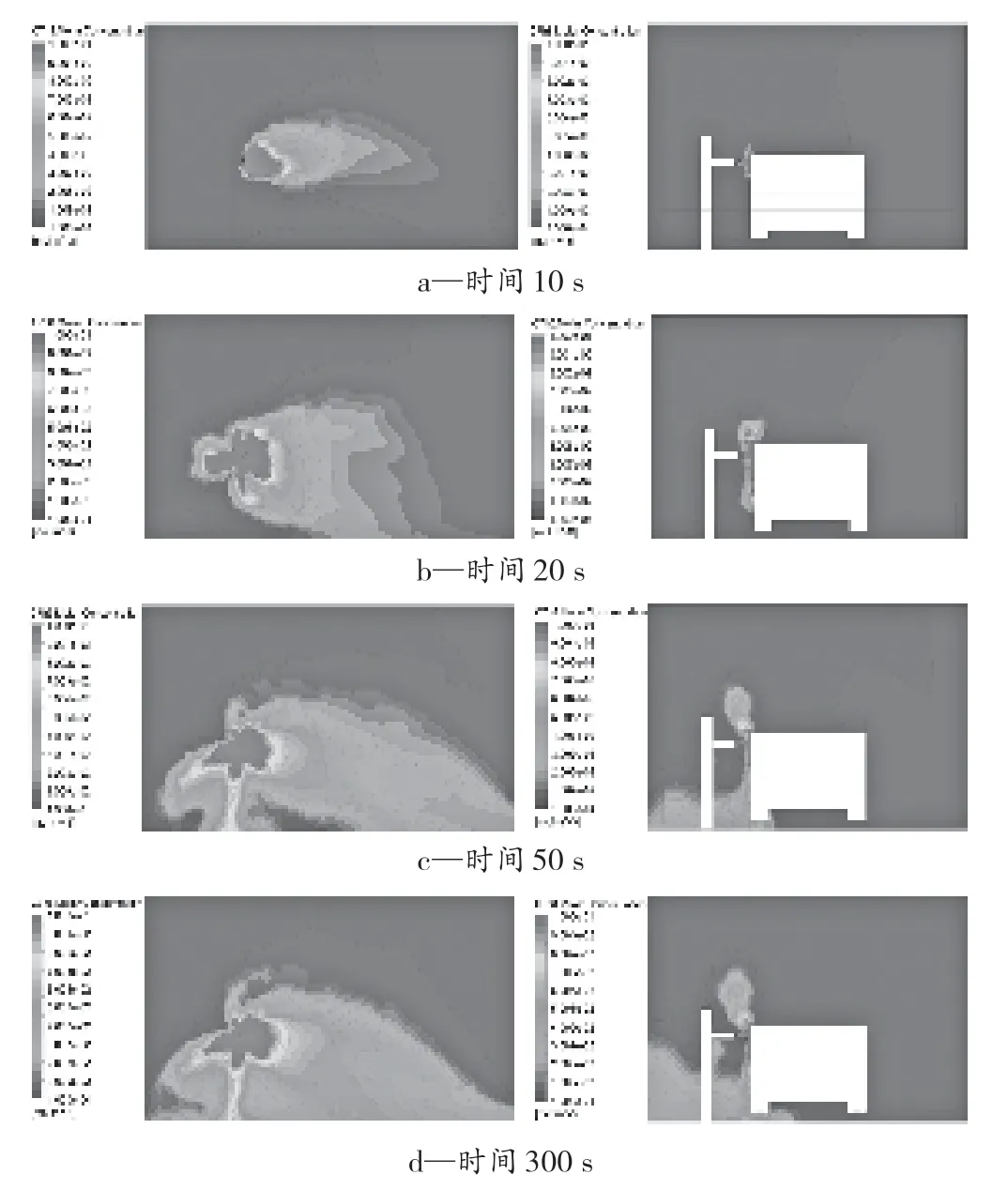
图3 y=1.75 m和x=1.7 m处VOC浓度随时间的变化情况Figure 3 VOC concentration distribution various with time at y=1.75 m and x=1.7 m

由图3可知，从开始喷漆到浓度场趋向于稳定阶段，由于VOC普遍密度大于空气，同时受到从左向右的气流组织的影响，所以VOC气体的流动形式为一种不断向前、向下流动的形式。经过计算，1 s时，涂装刚开始阶段，此时喷漆室内的VOC的平均物质的量的浓度仅为1.18×10-8mol/m3，浓度极低。10 s、20 s时，还处于发展状态，喷漆室内VOC的含量不断上升，同时在此阶段喷漆室内部的气流组织也在不断成型，VOC开始跟随运动的空气流向喷漆室右侧的出口处。从50 s前后一直到300 s，VOC浓度开始以较为缓慢的速率增长，在图中的表现即为50 s时的VOC浓度分布与300 s时的浓度分布变化不大，同时这也表示气流组织已经基本成型，已在喷漆室内形成了气流通路。时间达到300 s时，喷漆室内的VOC的平均物质的量的浓度为3.92×10-6mol/m3，涂装过程中VOC气体多数处于1.3 m的高度之下，由于气体离开喷枪时具有较高的动能，在遇到汽车涂装面时，涂装面上出现向各个方向溅射的现象，所以导致图中围绕涂装面出现一圈高VOC浓度分布的现象。

4.2 流体域速度场变化

图4为工况1（直线式60次/h）条件下，zx面上y=1.75 m以及yz面上x=1.7 m处流体速度随时间变化的情况。

图4 y=1.75 m和x=1.7 m处各时间段的速度分布Figure 4 Velocity distribution various with time at y=1.75 m and x=1.7 m

由图4可以发现，喷漆室内的速度场在50 s时已经基本趋于稳定，气流组织通路已经形成，室体内大部分区域的速度介于0.06 m/s与0.24 m/s之间。150 s与300 s时的速度场没有明显变化，室内大部分区域的速度介于0.18 m/s与0.36 m/s之间，并且速度场从排风口向送风口呈现出环形层状递减的分布形式。

4.3 瞬时捕集效率对比

仿真求解过程中对各工况排风口处以及枪口处从0～300 s全程的VOC流量随时间的变化进行了监控，并进行了数据处理，绘制瞬时捕集效率曲线图，如图5所示。

图5 瞬时捕集效率图Figure 5 Instantaneous capture efficiency

从图5各工况的瞬时捕集效率曲线可以发现，随着时间的变化，各工况的瞬时捕集效率逐渐增大到一定值之后就趋于稳定状态。不同的工况瞬间捕集效率达到稳定状态的时间不同，总体而言，直线式通风的瞬间捕集效率最早趋于稳定状态，一侧式（有利工况）通风次之，两侧式通风再次之，一侧式（不利工况）通风最后趋于稳定，这是四者之间形成不同的气流通路所导致的。此外，相同的气流组织形态下，通风量越大，瞬时捕集效率趋向于稳定的时间越短，这是由于换气次数越多，喷漆室内气流组织流动的速度就越快，那么相同时间内通过的流量越大，所以单位时间内排出室体外部的VOC的质量就越大，从而其趋向于稳定所需要的时间越短。

4.4 排污效率对比

室内VOC平均物质的量的浓度与排污效率如图6、7所示。

图6 室内VOC平均物质的量的浓度Figure 6 Average molar concentration of VOC

由室内VOC平均物质的量的浓度随时间的变化曲线（图6）可以看出，在70次/h与80次/h的换气次数下，一侧式（有利工况）通风方式室内VOC平均物质的量的浓度最低，两侧式通风较低，直线式通风较高，一侧式（不利工况）通风最高。而在60次/h换气次数下，两侧式通风方式具有最低的室内VOC平均物质的量的浓度。总体而言，一侧式（有利工况）通风方式室内VOC的平均物质的量的浓度最低，两侧式通风较低，直线式通风较高，一侧式（不利工况）通风最高。这意味着在使用相同的能源来维持同一通风量的情况下，一侧式（有利工况）通风要比其他3种通风方式在相同时间内排出更多的VOC，即一侧式（有利工况）通风方式对于能源的利用率最高。在同一种通风方式下，增加通风量可以进一步降低室内VOC的平均浓度，但是随着通风量的进一步增加，VOC平均浓度的下降幅度在逐渐减小，即能源的利用率会逐渐降低，所以在通风量不再是影响室内VOC平均浓度的主要因素时，还应考虑到其他因素的影响。

就排污效率（图7）而言，由于受到成型气流组织的影响，室内的VOC均会流向排风口，所以越靠近排风口VOC的浓度越高，也就导致了排污效率的值≥1，且该值越高，排污效果越好。图7中，一侧式（有利工况）排风要比其他3种排风方式具有更高的排污效率，并且通风量越大，排污效率越高，但是对于直线式、两侧式以及一侧式（不利工况）通风方式来讲，排污效率变化不明显，这是因为三者形成的气流组织较为稳定，导致VOC分布比较均匀，所以室内与出口处的VOC平均浓度相差不多，导致它们的比值比较接近，即排污效率变化不大。

图7 排污效率Figure 7 Discharge efficiency

5 结语

本研究利用计算流体力学的方法对开放式喷漆室的内部流场进行了研究，分析了4种通风方式的通风效果，得出结论如下：

（1）直线式通风方式喷漆室内VOC浓度最早趋于稳定，一侧式（有利工况）通风次之，两侧式通风方式再次之，一侧式（不利工况）最迟趋于稳定。在同一通风方式下，通风量越大，瞬时捕集效率越快趋向于稳定。

（2）在同一通风量下，一侧式（有利工况）通风方式室内VOC平均物质的量的浓度处于较低水平，一侧式（不利工况）通风方式室内VOC浓度最高，即一侧式（有利工况）通风方式对于能源的利用效率更高。在同一通风方式下，通风量越大，室内VOC平均物质的量的浓度越小，但通风量的增加与室内VOC平均物质的量的浓度的下降并不呈现明显的线性关系。

（3）一侧式（有利工况）通风方式具有更高的排污效率，且通风量越大，排污效率越高；其他3种通风方式而言，由于室内VOC的分布比较均匀，导致排污效率变化不大，但依旧符合上述规律。

（4）通过对各瞬时捕集效率、喷漆室内VOC平均物质的量的浓度以及排污效率的对比分析，一侧式（有利工况）通风方式虽然能够更好地排除喷漆室内的VOC气体，但考虑到喷漆过程中喷枪口并不会一直位于有利于通风的一侧，因此两侧式喷漆方式对于能源的利用效率会更高。在此通风方式下70次/h的通风量最为合理。