地震、波浪联合作用下深水大跨桥梁响应分析

2022-07-05苏京华柳春光

水利与建筑工程学报 2022年3期

苏京华，柳春光

(1.大连理工大学海岸与近海工程国家重点实验室，辽宁大连 116024；2.大连理工大学建设工程学部水利工程学院工程抗震研究所，辽宁大连 116024)

我国西部地区幅员辽阔，江河湖泊众多，为发展经济，建造了很多跨湖、跨河桥梁。刚构桥以其结构简单、造价低、刚度大、适用于跨度大的场地、造型美观等优点，被广泛应用于实际工程中[1]。由于西部地区沟壑纵横、多大峡谷，其中相当数量的刚构桥处于深水环境中。在地震作用时，桥梁结构会处于一个复杂的受力环境中，地震作用、波浪力、水流力等都会对桥梁结构产生影响。但目前对于这方面的研究还十分稀少，且结论尚未统一，因此本文以一整桥刚构桥有限元模型为例，以期丰富这一方面的科研内容。

地震作用对桥梁的影响主要以动水压力的形式体现。赖伟等[2]提出一种考虑表面波效应及流体压缩影响的半解析半数值方法计算地震作用下圆形截面桥墩所受的动水压力。刘振宇等[3-4]采用辐射波浪理论推导出圆形桥墩、矩形桥墩内外动水压力表达式，结果表明内外动水压力的不利影响需同时考虑，又提出墩-水耦合作用对桥梁横向地震动的影响程度更大。杨万理[5]基于辐射波浪法和流体单元法提出了一种新的基于混合法的正方形和矩形桥墩的外域动水压力表达式，基于频率降低的附加质量比法提出一种任意形状桥墩动水压力的方法。黄信等[6]比较了Morison方程与辐射波浪法所求得的动水压力对桥墩响应影响的差异；分析了考虑土-结构相互作用和双向地震作用两种情况下动水压力对桥墩结构响应的影响。李乔等[7]通过振动台试验数据提出使用附加刚度法模拟桥墩的弹性振动问题。

波浪作用下对于桥梁动力响应的研究已比较完善。李璐璐等[8]利用FLUENT模拟波浪并与试验对比验证了CFD计算群桩承台波浪力的适用性。柳春光等[9]指出在计算波浪作用对结构的动力响应时要考虑到波浪是否与结构频率相近而产生共振现象。

以上地震动水压力的研究均以静水环境为基础，对于考虑波浪等复杂环境下的研究相对较少。李忠献等[10]利用辐射波浪理论计算地震动水压力，以绕射波浪理论计算波浪力，分别就单独地震作用、单独波浪作用以及地震波浪联合作用三种情况下计算得出桥梁的动力响应，结果表明地震动水压力会增大结构的动力响应，波浪力的入射角度对结构响应的影响较小，联合作用时的动力响应并不是两者单独作用结果的简单叠加。林曾等[11]以一个圆形截面实体桥墩为例计算得出波浪地震联合作用时的动力响应较地震单独作用时小。吴安杰等[12]指出波流对在地震响应的影响最高可达63.5%。

本文以一个整体空心薄壁刚构桥为例，利用有限元软件ANSYS就单独地震作用、单独波浪作用及地震波浪联合作用三种情况对整桥进行动力响应时程分析，并考虑了有无内域水，不同水深、波长等情况对桥梁地震响应的影响。

1 计算方法

1.1 矩形空心桥墩地震动水压力计算方法

为平衡矩形空心桥墩内外压力，通常将桥墩做开洞处理，所以桥墩在地震作用时会同时受内、外动水压力影响。文献[3]指出内部动水压力对桥梁响应的影响不可忽略，应同时考虑两种动水压力。

本文采用文献[5]中的方法计算地震动水压力，基于辐射波浪法计算内域水地震动水压力，基于频率降低率的附加质量比法计算外域水地震动水压力。

(1) 内域水动水压力微分方程如式(1)所示：

(1)

基本假定为：

① 不考虑阻尼影响

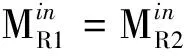
结果如式(2)所示：

(2)

(2) 外域水动水压力自由运动方程如式(3)所示：

(3)

其中：Ma为附加质量。

不考虑动水压力的自由微分方程如式(4)所示：

(4)

求解式(3)、式(4)得出频率降低率并拟合得到矩形截面桥墩附加质量比为：

p(h,D,lab)=[0.017ln(D)ln(h)+0.024ln(h)-

0.1ln(D)+0.34]×lab0.0434ln(h)-0.0028Dlnh-1

(5)

其中：L为外域非迎水面宽度；D为迎水面宽度；lab=L/D为长宽比。

单位高度外水附加质量为：

Ma=ρconD2p(h,D,lab)

(6)

其中：ρcon为桥墩质量密度。

1.2 矩形桥墩波浪力计算方法

对于圆形截面大尺度结构(D′/L′>0.2)波浪力的求解采用绕射波浪理论计算，其中D′为桥墩直径，L′为波长。依据绕射波浪理论，结构受波浪扰动后的速度势可以视为入射波场与散射波场的叠加[13]。

φ=Φe-iωt=(ΦI+ΦS)e-iωt

(7)

任意高度z处的波浪力如式(8)所示：

(8)

(9)

沿高度方向积分计算桥墩所受的总力的大小为：

(10)

弯矩大小为：

cosh(kh)+1)×A(kD′)sin(ωt-α)

(11)

则波浪力作用点距桥墩底部的距离为：

(12)

依据《海港水文规范》[14](JTS145—2013)提供的方法将矩形截面转化为圆形截面计算。

(13)

其中:d为换算后直径。

1.3 地震、波浪联合作用运动方程建立

目前对于地震、波浪二者耦合作用下的计算方法研究基本处于空白阶段，文献[10-11,15]给出了两者在联合作用时动力方程的叠加方法。本文依托于有限元软件ANSYS中的时程分析实现对结构响应的计算。

地震作用时的运动方程如式(14)所示：

(14)

波浪作用时的运动方程为：

(15)

当地震、波浪联合作用时结构的运动方程可写作：

(16)

结构阻尼采用Rayleigh阻尼形式：

C=αM+βK

(17)

其中:ω1、ω2为结构第一阶与第二阶自振圆频率;ζ1、ζ2为第一阶与第二阶自振圆频率相对应的阻尼比。

依据本章1.1与1.2小节的计算方法求得附加质量与波浪力，将其代入式(16)便可得出联合作用时的运动方程表达式。

2 计算模型

桥梁主桥孔跨尺寸为120 m+220 m+120 m，桥面宽度11 m，刚构桥桥墩为矩形变截面空心薄壁墩，主墩顺桥采用1∶100放坡，横桥向采用1∶80放坡，壁厚采用0.7 m、0.8 m及0.9 m变截面壁厚；辅助桥墩顺桥向与横桥向均采用1∶80放坡，壁厚采用0.6 m、0.7 m及0.8 m变截面壁厚。主梁为变高度直腹式箱型梁，主墩墩顶处梁高14.5 m，跨中及辅助墩墩顶梁高4.5 m，最高蓄水位为165 m。桥墩尺寸如表1所示，桥梁模型如图1所示。

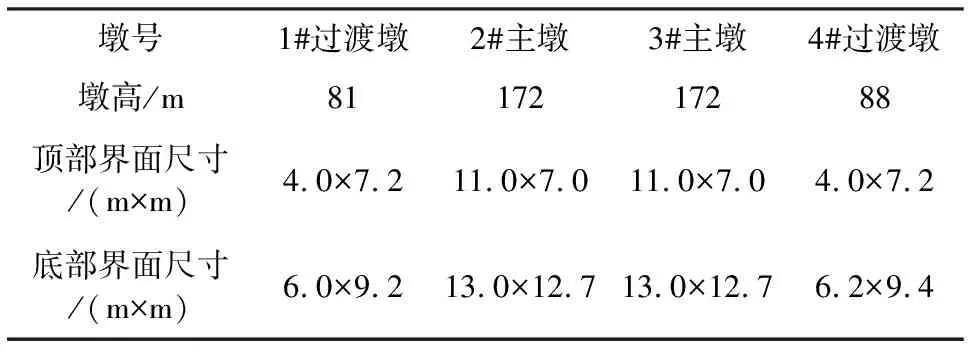
表1 桥墩尺寸表

图1 桥梁结构模型图

桥梁整体采用壳单元中的SHELL181单元模拟，地震动水压力以求得的附加质量转化为附加密度施加于结构之上。主墩(2墩、3墩)与主梁刚接，辅助墩(1墩、4墩)与主梁利用弹簧单元连接，桥墩底部与地面刚接，结构整体采用C50混凝土，其桥梁模拟参数主要有三项，如表2所示。整体结构以横桥向为x轴，竖向为y轴，顺桥向为z轴建立模型。地震波作用于桥墩底部固结处，波浪力作用点依据计算得出。

表2 桥梁结构参数表

3 桥梁动力响应分析

3.1 有水、无水工况下结构动力特性比较

为对比地震作用下水对桥梁结构动力特性的影响，本文选取有水(165 m)及无水(0 m)工况下前五阶自振频率作为参照。表3为结构自振频率对比结果。

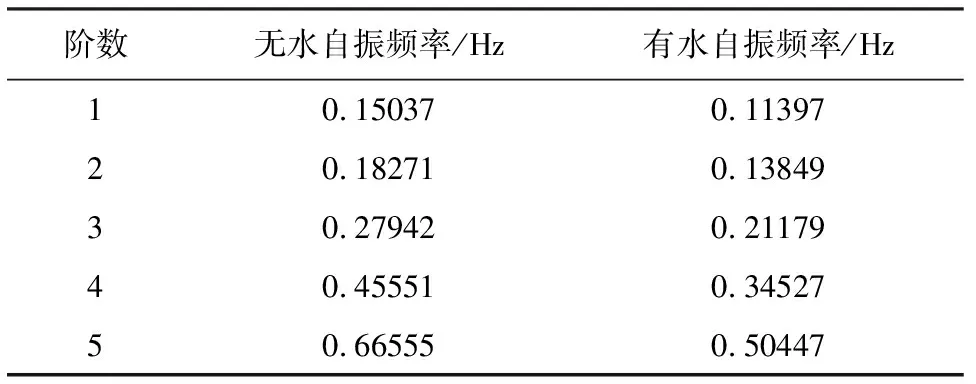
表3 有、无水工况下结构自振频率表

由表3可以看出，附加质量的存在改变了结构的自振频率，且对自振频率影响较大，水的存在减小了结构的自振频率，基频由无水时的0.150 37改变为有水时的0.113 97，变化幅值为-24.2%。这是由于本文中水的影响是以附加密度的形式加到结构上的，密度的增加使得结构质量增大从而减小了结构的自振频率，且由于该桥梁结构通体为空心薄壁结构，体积较大而质量小，因此附加质量相对于结构本身的质量来说不可忽略，对结构自振频率的影响也较大。

3.2 仅地震作用时的动力响应

利用辐射波浪法和基于频率降低率的附加质量比法计算桥梁结构地震作用时静水对其产生的附加质量，取El Centro波与天津波沿横桥向输入，通过调幅将地震波峰值加速度取为0.1g，El Centro波时间步长为0.02 s，取前30 s作为研究对象，天津波时间步长为0.01 s，取前19.2 s作为研究对象，两种波的加速度时程曲线如图2、图3所示，本文以天津波作为主要研究对象，同时考虑有无水、内外水、水深等情况下动力响应的差异，以下所列动力响应曲线均为天津波作用下的结果。汶川地震时，庙子坪岷江大桥桥墩深水区位置开裂，修复困难[16]，因此本文着重关注主墩的动力响应。

图2 天津波加速度时程曲线

图3 El Centro波加速度时程曲线

为得出水深对桥梁结构响应的影响程度，分别就无水、满水(165 m)、半水(82.5 m)三种情况进行分析，三种情况均同时考虑内外域水，分别计算出内外域水产生的附加密度，将其叠加后同时施加到结构上。表4为不同水深情况下结构各位置处位移与应力响应结果。图4与图5为天津波作用时三种工况下主墩墩顶与辅助墩墩顶的位移时程曲线。

表4 结构各位置在不同水深时的动力响应

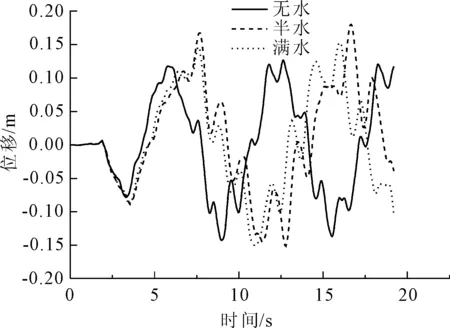
图4 2墩顶位移时程曲线

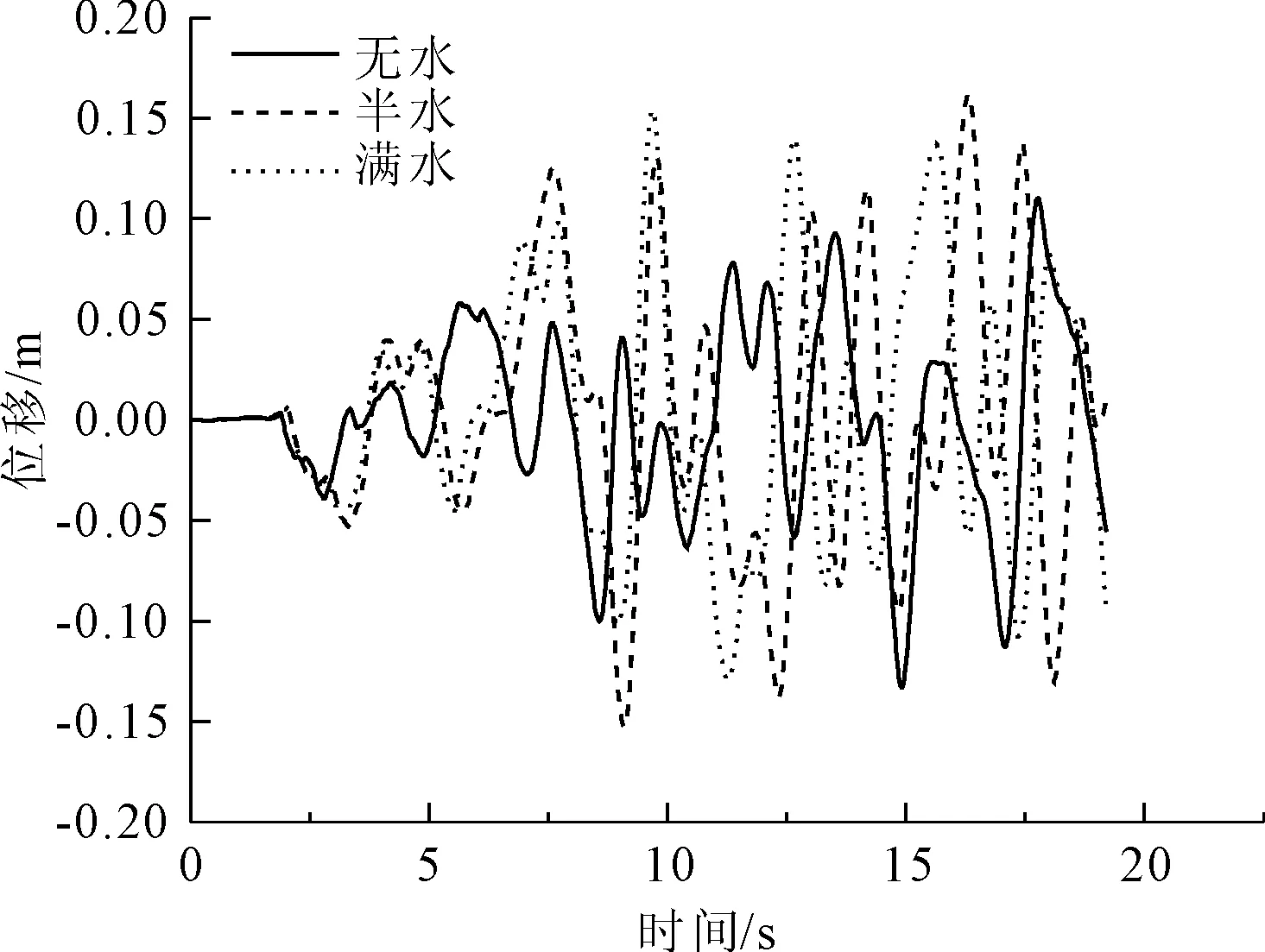
图5 1墩顶位移时程曲线

由表4可以看出，水的存在增大了结构的位移与应力响应，以天津波为例，半水情况下，主墩位移由无水情况下的142.9 mm增加到180.4 mm，增幅为26.24%，主墩墩底应力由无水情况下的4.14 MPa增加到7.36 MPa，增幅为77.8%；满水状态下，主墩位移由142.9 mm增至153.2 mm，增幅为7.2%，主墩墩底应力由4.14 MPa增至6.72 MPa，增幅为62.3%。水对桥梁动力响应的影响主要是由惯性力与阻尼力两部分组成的，在入水深度不大时，主要由惯性力起作用，水的存在极大地增加了结构的动力响应；而当水深过大时，如满水状况下，水几乎将整桥淹没，阻尼力起到了一定的作用，使得桥梁结构响应幅值有所下降。因此对于整桥结构来说，水的存在增大了结构的动力响应，但其增幅存在先增大后减小的情况。对于El Centro波有相同结论。

考虑内域水对结构响应的影响，就满水情况下进行讨论。表5为分别有无内域水情况下结构的响应情况。

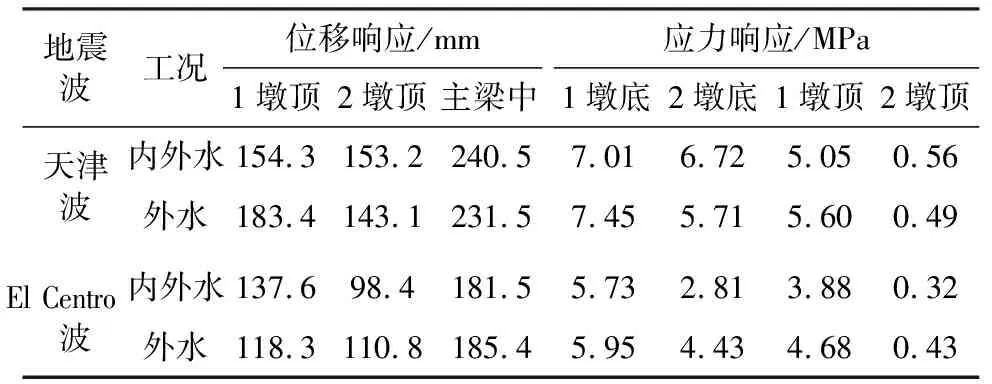
表5 有无内域水时结构动力响应

由表5可得内域水对结构动力响应的影响不可忽略，以主墩动力响应为例，天津波作用条件下，仅外域水作用时结构的位移响应为143.1 mm，内外域水作用下结构位移响应为153.2 mm，内域水的影响程度为7.1%；外域水作用下主墩墩底的应力响应为5.71 MPa,内外域水同时作用下的应力响应为6.72 MPa，内域水的影响程度为17.7%。El Centro波条件下，仅外域水作用时结构位移响应为110.8 mm，内外域水作用下位移动力响应为98.4 mm，内域水影响程度为-11.2%。外域水作用下主墩墩底的应力响应为4.43 MPa,内外域水同时作用下的应力响应为2.81 MPa，内域水的影响程度为-38.8%。由此可得内域水对主墩的影响较大，最高可达38.8%，因此结构计算时内域水不可忽略，需同时考虑内外域水，结论与文献[3]相似。且内域水对结构动力响应的影响为增大或减小与地震动特性有关。

3.3 仅波浪作用时的动力响应

表6 波浪作用动力响应

图6 40 m波浪作用下结构各点位移曲线

图7 30 m、40 m、50 m波浪下2墩墩顶位移曲线

由图6可得，同一波浪作用下，各点位移曲线周期相同，波浪作用对辅助墩、主墩及主梁跨中位移的影响程度是依次递增的，这是由于主墩相较于辅助墩来说墩高较大，结构更柔，因此位移较大，而跨中位移最大则是由于跨中底部无墩柱连接，无法约束其横向位移，因此波浪作用下，辅助墩、主墩、跨中位移依次增大。图7可以看出，不同波长波浪作用下，同一节点处位移峰值出现时刻不同，响应大小不同。这是由于波长为30 m时，波浪周期为4.386 s，频率为0.228，波长为40 m时，波浪周期为5 s，频率为0.2；波长为50 m时，波浪周期为5.66 s，频率为0.176。因此波长较长的波浪峰值出现较晚，而波长的增大还会减小波数，从而增大波浪力的大小，波长为50 m时频率更接近结构基础频率0.150 37，更接近共振频率，这些因素都使得结构响应增大。由表6中1墩墩顶的应力数据为例，波长从30 m到40 m时，应力由0.028 MPa变为0.350 MPa，增大12.5倍，变化显著，波长从40 m到50 m时，应力由0.35 MPa变为0.69 MPa，增大1.97倍，由此可以得出除去波长因素的影响，波长为30 m的波浪几乎不受结构共振的影响，以此为研究对象得出的结论更具有普遍性。

3.4 波浪、地震联合作用时的动力响应

为规避波浪作用时波浪与结构共振情况的产生，本文就半水情况下、同时考虑内外域水、波长为30 m情况为例，考虑波浪、地震联合作用对结构动力响应的影响。表7为仅地震、仅波浪与联合作用时桥梁结构各点动力响应结果，图8、图9为三种工况下跨中与主墩墩顶位移时程曲线。

表7 地震、波浪联合作用时的动力响应

图8 1墩顶位移图

图9 2墩顶位移图

以天津波为例，由表6可得，仅考虑波浪作用时，主墩墩顶的位移为17.8 mm，墩底应力为0.073 MPa，地震作用下，主墩墩顶的位移为180.4 mm，墩底应力为7.36 MPa，地震、波浪联合作用时，主墩墩顶的位移为180.5 mm，墩底应力为10.2 MPa。由此可见，波浪的存在在一定程度上影响了结构的地震响应，仅波浪作用时的动力响应较仅地震作用时小。波浪对于结构位移响应的影响较小，对应力响应的影响较大，主墩墩底应力增幅为38.6%，因此波浪的作用不可忽略，由图8、图9可以较为明显地看出联合作用时，位移曲线形状与地震作用时相似，说明联合作用时，地震作用的影响更大。对于El Centro波有相同结论。

为分析地震作用及联合作用对结构本身的影响，以天津波为例，讨论在仅地震作用无水工况、半水工况及联合作用半水工况条件下，主墩墩顶加速度变化情况，图10为墩顶加速度时程曲线。

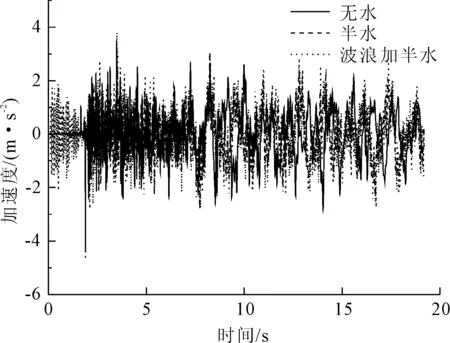
图10 主墩墩顶加速度时程曲线

其中，仅地震作用无水工况下，峰值加速度为4.3 m/s2，半水工况下峰值加速度为4.27 m/s2，水的存在减小了结构的峰值加速度，这是由于水的存在增大了结构本身的柔度与阻尼，使得峰值加速度减小，以上结论佐证了3.1小节的结论。地震波浪联合作用工况下，结构峰值加速度为4.49 m/s2，较仅地震作用半水工况下的峰值加速度增幅为5.1%，这是由于波浪作用的存在，增大了结构的受力，从而使得结构峰值加速度有了一定程度的增大，该结论佐证了3.4小节关于波浪对地震响应影响的结论。